Разбиение натурального ряда
Отдел образования администрации Центрального района
Муниципальное общеобразовательное учреждение
Средняя общеобразовательная школа № 4
Секция математика
НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
По теме
Разбиение натурального ряда
Сорока Александра Александровна
Василькова Евгения Сергеевна
Учащихся 11 В класса МОУ СОШ №4
Центрального района
8-905-958-2583
8-913-954-3357
Руководитель: Тропина Наталья
Валерьяновна,
Кандидат педагогических наук
доцент кафедры математического анализа
НГПУ
(работа выполнена в МОУ СОШ №4)
Новосибирск 2008г.
Содержание
Введение
§1. Основные понятия и определения
§2. Две последовательности. Их свойства
§3. Упражнения
§4. Геометрическая интерпретация
§5. Некоторые приложения (Палиндромы)
Заключение
Список литературы
рациональный иррациональный число
ВВЕДЕНИЕ
Целью данной работы является изучение вопроса о разбиениях натурального ряда на две непересекающиеся возрастающие последовательности.
Работа состоит из пяти параграфов:
Первый параграф посвящен понятиям и определениям, которые пригодятся нам в работе.
Во втором параграфе идет речь о построении двух последовательностей и о гипотезе Акулича.
В третьем параграфе приведены упражнения.
Четвертый параграф посвящен геометрической интерпретации построения последовательностей.
В пятом параграфе приведены некоторые приложения.
§1 Основные понятия и определения
Целая и дробная части числа
Определение 1. Целой частью числа x называется наибольшее целое число r, не превышающее x.
Целая часть числа x обозначается символом [x] или (реже) E(x) (от фр. entier "антье" — целый).
Если x принадлежит промежутку
[r; r +1),
где r — целое число, то [x]=r, т.е. x находится на промежутке [ [x]; [x]+1). По свойствам числовых неравенств, разность x-[x] будет на промежутке [0; 1).
Определение 2. Число q = x - [x] называют дробной частью числа x и обозначают {x}. Следовательно, дробная часть числа всегда неотрицательна и не превышает 1, тогда как целая часть числа может принимать как положительные значения, так и неположительные. Таким образом {x} = x - [x], а, следовательно, x = [x] + {x}.
Примеры
-
[5]=5
[7,2]=7
[-3]=-3
[-4,2]=-5
[0]=0
{5}=0
{7,2}=0,2
{-3}=0
{-4,2}=0,8
{0}=
Свойство целой части
[x+n] = [x]+n
где n – натуральное число
Рациональные и иррациональные числа и их свойства
Определение 3.Рациональным числом называется число, которое можно представить в виде дроби

где m – целое число, а n – натуральное.
Определение
4. Если число не представимо в виде
 ,
то такое число называется иррациональным.
,
то такое число называется иррациональным.
Теорема 1. Любое рациональное число представимо в виде конечной или бесконечной периодической дроби.
Любое иррациональное число представимо в виде бесконечной десятичной непериодической дроби.
Примеры
0,5=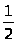 -рациональное
число
-рациональное
число
0,(3)=
 -
рациональное число
-
рациональное число
1,0123456789101112…-иррациональное число
 -
иррациональное число
-
иррациональное число
Свойства арифметических действий над рациональными и иррациональными числами
1. Если
 -
рациональные числа, то
-
рациональные числа, то
 ,
,
 ,
,
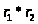 ,
,
 ,
, - рациональные числа.
- рациональные числа.
Дано: Доказательство
 ;
;
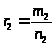
 - рациональное
- рациональное
2. Если
r-рациональное
число,
 -иррациональное
число, то
-иррациональное
число, то
 - иррациональные
числа.
- иррациональные
числа.
Доказательство: (от противного)
Предположим что
 но
но
 -
противоречие
-
противоречие
3. Если
 ,то
про
,то
про
 ничего определенного нельзя сказать.
ничего определенного нельзя сказать.
Примеры

§2 Две последовательности. Их свойства
В этом параграфе речь пойдет о задачах, посвященных разбиению натурального ряда на последовательности и о теореме, доказывающей их.
Рассмотрим один из способов разбиения натурального ряда на две возрастающие непересекающиеся последовательности
 и
и
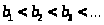
которые при
любом натуральном n
удовлетворяют условию
 .
.
Двигаясь по натуральному ряду, можем последовательно вычислять члены обеих последовательностей.

Поскольку все
 ,
то наименьшее натуральное число, т.е.
1- должно равняться
,
то наименьшее натуральное число, т.е.
1- должно равняться
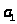 .
.
Следовательно

и так далее.
Каждый раз, выбирая наименьшее
неиспользованное натуральное число и
считая его равным
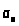 ,
затем, находя
,
затем, находя
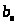 по
формуле
по
формуле

можем строить последовательности.
В 1877 году в «Теории звука» лорд Рэлей писал: «если x есть некоторое положительное иррациональное число, меньшее единицы, то можно взять два ряда величин n/x и n/(x-1) где n = 1,2,3…; каждое число, принадлежащее к тому или иному ряду, и только оно одно, будет заключено между двумя последовательными натуральными числами”. Т.е.
 и
и

заполняют без пропусков и перекрытий весь натуральный ряд, если
0<x<1
и x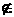 Q
Q
Гипотеза Акулича и явные формулы
И.Ф. Акулич предложил гипотезу: отношение количества a-чисел к количеству b-чисел стремится к «золотому сечению»
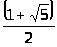
(где a-числа
– числа, принадлежащие последовательности
 ,
b-числа-
числа, принадлежащие последовательности
,
b-числа-
числа, принадлежащие последовательности
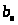 ).
).
 [(1+
[(1+ )n/2]
)n/2]
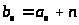 =[(1+
=[(1+ )n/2]+n=[(3+
)n/2]+n=[(3+ )n/2]
)n/2]
Выведем из явных формул гипотезу Акулича.
Обозначим
 ;
;
Рассмотрим натуральное число N и выясним сколько a-чисел и b-чисел среди первых N натуральных чисел, если последовательности заданы формулами:

 ;
;
Неравенства
 равносильно,
по определению целой части, неравенству
равносильно,
по определению целой части, неравенству
 <N+1,
т.е. неравенству n<(N+1)/
<N+1,
т.е. неравенству n<(N+1)/ .
Значит, a-чисел
среди первых N
натуральных чисел имеется ровно
[(N+1)/
.
Значит, a-чисел
среди первых N
натуральных чисел имеется ровно
[(N+1)/ ].
Аналогично, b-чисел
].
Аналогично, b-чисел
[(N+1)/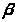 ]
]
Тогда отношение количества a - чисел к количеству b- чисел равно

Устремим N к бесконечности, получим

Гипотеза
оказалась верна, при условии что обе
последовательности
 и
и
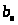 заданы явными формулами
заданы явными формулами
 [(1+
[(1+ )n/2]
)n/2]
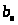 =[(3+
=[(3+ )n/2]
)n/2]
Но Акулич не
первый догадался представить
последовательности
 и
и
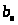 в виде [
в виде [ ]
и [
]
и [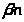 ].
].
Эти же явные
формулы получаются из формул Рэлея при
x
= 2/(1+ ),
поскольку при этом величина 1-x
равна как раз 2/(3+
),
поскольку при этом величина 1-x
равна как раз 2/(3+ ),
т.е.
),
т.е.

Возникает вопрос об единственности разбиения множества N на две последовательности.
В статье Баабабова [2] доказывается теорема, обобщающая этот результат и утверждает, что таких разбиений натурального ряда существует бесконечно много. Приведем данную теорему и ее подробное доказательство.
Обозначим

Теорема.
Если
 и
и
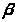 - положительные иррациональные числа,
связанные соотношением
- положительные иррациональные числа,
связанные соотношением
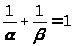 ,
то среди чисел вида [
,
то среди чисел вида [ ]
и [
]
и [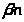 ]
, где n
]
, где n
 ,
каждое натуральное число встречается
ровно один раз.
,
каждое натуральное число встречается
ровно один раз.
Доказательство:
Поскольку
 >
1, в последовательности
>
1, в последовательности
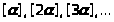 никакое число не повторяется. Аналогично
вследствие неравенства
никакое число не повторяется. Аналогично
вследствие неравенства
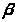 >1
строго возрастает и последовательность
>1
строго возрастает и последовательность

Действительно,
пусть [ ]
– k
]
– k

Следовательно,
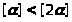
Докажем теперь, что каждое натуральное число встречается ровно один раз.
Предположим,
что некоторое натуральное число k
вошло в обе последовательности т е k
=
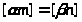 ,
где m,n
– натуральные числа. Тогда должны быть
выполнены неравенства
,
где m,n
– натуральные числа. Тогда должны быть
выполнены неравенства
k< <
k + 1, k<
<
k + 1, k<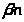 <k
+ 1,
<k
+ 1,
т.е.


сложим эти неравенства, не забывая про условие
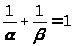
Получим
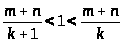
откуда k<m+n<k+1
Но такого для натуральных чисел не может быть. Значит, число k не могло войти в обе последовательности.
Теперь предположим, что k не вошло ни в одну из последовательностей. Тогда для некоторых натуральных чисел m и n должны выполняться неравенства
 m
< k
<k+1<
m
< k
<k+1<
 (m+1)
(m+1)
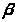 n
< k
<k+1<
n
< k
<k+1<
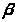 (n+1)
(n+1)
которые можно преобразовать к виду

складывая, получаем

откуда m+n<k
и k+1<m+n+2
 m+n<k
и m+n>k-1
m+n<k
и m+n>k-1
Такого для натуральных чисел тоже не может быть. Получаем противоречие, следовательно, теорема доказана.
В следующем параграфе рассмотрены упражнения о разбиениях натурального ряда, при решении которых используются результаты данного параграфа.
§3. Упражнения
Упражнение 1
Пусть последовательность задана формулой
 .Найти
.Найти
 .
.
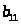
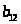

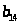




1 … 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48


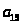





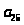

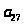
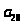
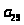

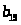
49 50

Используя эту
формулу, можно найти любое a .
.
Упражнение 2.
Вычислить
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
[(1+ |
1 |
3 |
4 |
6 |
8 |
9 |
11 |
12 |
14 |
16 |
17 |
19 |
21 |
22 |
24 |
25 |
27 |
29 |
|
[(3+ |
2 |
5 |
7 |
10 |
13 |
15 |
18 |
20 |
23 |
26 |
28 |
31 |
34 |
36 |
39 |
41 |
44 |
47 |
Упражнение 3
Используя формулы
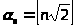 и
и

постройте последовательности, которые заполняют весь натуральный ряд без пропусков и перекрытий
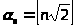
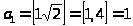 ,
,
 ,
,
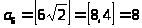 …
…
… ,
,
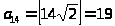 ,
,
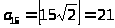 …
…






1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21




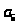

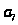





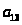
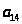

Где

Упражнение 4
Найти явные
формулы для возрастающих последовательностей
 и
и
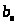 ,
заполняющих натуральный ряд без пропусков
и перекрытий и удовлетворяющих соотношению
,
заполняющих натуральный ряд без пропусков
и перекрытий и удовлетворяющих соотношению
 при всех n=
1,2,3…
при всех n=
1,2,3…


Итак, явные формулы для последовательностей доказаны.
§4. Геометрическая интерпретация
Удивительно простое и наглядное доказательство теоремы из § 1 получаем, если рассмотрим геометрическую интерпретацию.

Пусть, как и ранее, α и β – положительные иррациональные числа.
Причем
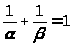 .
Тогда
.
Тогда
 ,
откуда
,
откуда
 .
.
Нарисуем на листе бумаги, как на координатной плоскости прямую l, заданную уравнением у=(α-1)x, которое можно записать так же в виде x=(β-1)y.
Занумеруем подряд все клетки, которые пересекают l, начиная с нулевой клетки, которой принадлежит начало координат (для … взято
α= )
)
Если мы обозначим числа, стоящие над линией за a- числа, а под линией за b – числа то получатся две последовательности, о которых мы говорили в §1.
Поскольку число α иррационально, прямая l не проходит через узлы сетки. Значит, l входит в очередную клетку либо слева, пересекая вертикальную линию сетки, либо снизу, пересекая горизонтальную линию.
Если l вошла в клетку слева и пересекла при этом вертикаль х=n, то номер клетки, в которую при этом вошла прямая равен n+[( α-1)n]=[ αn].
Если же прямая l пересекла снизу горизонталь y=m, то номер соответствующей клетки равен [(β-1)m]+m=[βm].
§5. Некоторые приложения. Палиндромы
Обозначим
натуральные числа принадлежащие
последовательности a буквой А, а принадлежащие последовательности
буквой А, а принадлежащие последовательности
 -
буквой В.построим последовательность.
-
буквой В.построим последовательность.
АВААВАВААВААВАВААВАВААВААВАВААВААВАВААВАВААВАВАВА…
Рассмотрев последовательность повнимательнее, заметим, что ее можно разделить на палиндромы.
Определение: Палиндромы (перевертыш) – это слово, которое выглядит одинаково при чтении слова как слева направо, так и справа налево.
Примеры:
Шалаш, ротор или АВВАВАВВА.
Рассмотрим задачу, связанную с палиндромами (аналогичную задачу решал в своей статье Акулич)
Из букв А и В составлено 2010-буквенное слово. Докажите, что его можно разбить менее чем на 900 более коротких слов, каждое из которых является палиндромом.
Возьмем произвольное 2010-буквенное слово и разобьем его сначала на 5-буквенные – их будет всего 402. Каждое из этих 5-буквенных слов, в свою очередь, может быть составлено не более чем из двух палиндромов. Поэтому произвольное 2010-буквенное слово можно составить не более чем из 804 палиндромов, т.е. меньше чем из 900, что и требовалось доказать.
Чтобы решать такие задачи в общем виде, введем функцию f(n).Через нее обозначим такое наименьшее натуральное число, что всякое слово длиной n, составленное из букв А и В может быть разбито не более чем на f(n) палиндромов.
Упражнение 1
Придумайте слово из букв А и В которое нельзя разбить менее чем на 3 палиндрома, но которое после приписывания к нему справа или слева любой из букв А и В можно разбить на два палиндрома.
АВААВВ+А
Оказалось, что задачи можно решить в общем виде. Введем функцию f(n).
Через f(n) обозначим такое наименьшее число, что всякое слово длиной n, состоящее из букв А и В, может быть разбито не более чем на f(n) палиндромов.
Пример:
Найдем f(6).
Всего шестибуквенных слов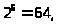 но
поскольку буквы А и В равноправны
достаточно рассмотреть только слова
начинающиеся на букву А
но
поскольку буквы А и В равноправны
достаточно рассмотреть только слова
начинающиеся на букву А
АААААА
ААААА+В
ААА+АВА
АААА+ВВ
А+ААВАА
ААА+ВАВ
АА+АВВА
ААА+ВВВ
ААВАА+А
АА+ВААВ
А+АВАВА
АА+ВАВ+В!
ААВВАА
А+АВВА+В!
А+АВВВА
АА+ВВВ
АВА+ААА
А+ВАААВ
АВА+АВА
АВА+А+ВВ!
АВАВА+А
АВАВА+В
АВА+ВВ+А!
АВА+ВВВ
АВВА+АА
АА+ВААВ
АВВА+В+А!
АВВА+ВВ
АВВВА+А
АВВВА+В
АВВВВА
А+ВВВВВ
Восклицательными знаками отмечены слова, которые нельзя разбить менее чем на три палиндрома. Ясно, что всякое шестибуквенное слово можно разбить не более чем на три палиндрома. Ниже приведем 10 значений функции f
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
f(n) |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
4 |
4 |
4 |
|
n/f(n) |
1 |
1 |
1.5 |
2 |
2.5 |
2 |
2.33 |
2 |
2.25 |
2.5 |
n/f(n) – это средняя длина палиндромов, на которые разбито самое трудно разбиваемое n- буквенное слово.
Упражнение 2
Для каждого n- 1,2,3,…10 укажите слово длиной n из букв А и В, которое нельзя разбить менее чем на f(n) палиндромов.
n=1 А
n=2 ВВ
n=3 АВВ
n=4 ААВВ
n=5 АВАВВ
n=6 АВААВВ
n=7 ВАВААВВ
n=8 ВВААВВАА
n=9 АВАВАВААВ
n=10 АВАВАВАВВВ
В статье А. Баабабоваприведена теорема:
При любом натуральном n имеем f(3n)=n+1, f(3n+1)=n+1, f(6n+2)=2n+2.при любом натуральном n>1 имеем f(6n+5)=2n+2, исключительное значение f(11)=5.
Следствие из теоремы
Предел
 существует и равен 3.
существует и равен 3.
Каждое слово из n букв А и В может быть разбито не более чем на [(n+4)/3] палиндромов.



4)f(6k+5) = 2k+2
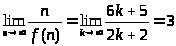 .
.
Итак, в каждом из случаев получаем один и тот же предел 3.
Следовательно

ЗАКЛЮЧЕНИЕ
В процессе работы над темой нами были изучены вопросы о разбиениях натурального ряда на две непересекающиеся возрастающие последовательности, также были решены самостоятельно 6 упражнений, доказано следствие к теореме из § 3.
Литература
1. Акулич И.Ф. Ум хорошо, а пять лучше // Квант. – 1998. - №6
2.Баобабов А. «Пентиум» хорошо, а ум лучше // Квант.-1999. - №4,№5
3. Зайцев В.В., Рыжков В.В., Сканави М.И. Элементарная математика М.Наука, 1976
4. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра 8 класс. М. Просвещение, 1996