Методические материалы по учебной дисциплине "Высшая математика" для студентов I курса заочной формы обучения
Институт предпринимательства и современных технологий
МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ
«Высшая математика»
ДЛЯ СТУДЕНТОВ I КУРСА ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
ПО СПЕЦИАЛЬНОСТИ «Финансы и кредит»
ЧастьI
Житомир
1999
Методические материалы по учебной дисциплине "Высшая математика" для студентов I курса заочной формы обучения по специальности "Финансы и кредит" (Часть I).
Составили: Шумко Л.И., кандидат технических наук, доцент;
Шумко Л.Г., кандидат технических наук, доцент;
Коваль Т.Л., кандидат физико-математических наук.
Рецензент: Нестерчук А.В., кандидат физико-математических наук, доцент, зав.кафедрой математического анализа Житомирского государственного педагогического университета им.И.Франка.
Житомир: ИПСТ, 1999
Введение
Настоящие методические указания предназначены для студентов-заочников специальностей "Финансы и кредит" и "Информационные системы в менеджменте", для которых учебным планом предусмотрено изучение общего курса высшей математики в объеме 180 учебных часов. Методические указания содержат рабочую программу курса высшей математики, общие рекомендации по изучению дисциплины, краткие указания к выполнению контрольных работ, образцы решения некоторых задач, контрольные задания. Вопросы для самопроверки более подробно расшифровывают программу курса и позволяют студентам-заочникам проверить уровень своей подготовленности по каждой теме программы общего курса высшей математики.
Общие методические указания.
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом: чтение учебников. решение задач, выполнение контрольных заданий. Если в процессе изучения материала или при решении задач у студента возникают трудности. то можно обратиться к преподавателю кафедры высшей математики для получения консультации. После изучения определенной темы по учебнику, решения задач необходимо ответить на вопросы для самопроверки, помещенные в конце темы.
В соответствии с действующим учебным планом студенты-заочники изучают курс высшей математики в течение 1 и 2 семестра и выполняют в каждом семестре по две контрольные работы.
Первая и вторая контрольные работы выполняются студентами в 1 семестре после изучения тем 1-2 и 3-4 соответственно.
Третья и четвертая контрольная работа выполняются студентами во 2 семестре после изучения тем 5-7 и 8-9 соответственно.
При выполнении контрольных работ студент должен руководствоваться следующими указаниями:
1. Каждая работа должна выполняться в отдельной тетради (в клетку), на внешней обложке которой должны быть ясно написаны фамилия студента, его инициалы, полный шифр, номер контрольной работы, дата ее отсылки в институт, домашний адрес студента.
2. Контрольные задачи следует располагать в порядке номеров. указанных в заданиях. Перед решением каждой задачи надо полностью переписать ее условия.
3. Решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых формул, теорем.
4. Решение задач геометрического содержания должно сопровождаться чертежами, выполненными аккуратно, с указанием осей координат и единиц масштаба. Объяснения к задачам должны соответствовать обозначениям, приведенным на чертежах.
5.На каждой странице тетради необходимо оставлять поля шириной 3-4см для замечаний преподавателя.
6.Контрольные работы должны выполняться самостоятельно. Не самостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме. Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена.
7.Студент выполняет тот вариант контрольной работы. который совпадает с последней цифрой его учебного шифра.
Ниже приведены таблицы номеров задач для контрольных работ.
1. При четырех контрольных работах по учебному плану:
|
Номера задач для контрольных заданий |
||||
|
№ |
|
2 |
3 |
4 |
|
1 |
1, 11, 21, 31, 41 |
51, 61, 71, 81, 91 |
101, 111, 121, 131 |
141, 151, 161, 171 |
|
2 |
2, 12, 22, 32, 42 |
52, 62, 72, 82, 92 |
102, 112, 122, 132 |
142, 152, 162, 172 |
|
3 |
3, 13, 23, 33, 43 |
53, 63, 73, 83, 93 |
103, 113, 123, 133 |
143, 153, 163, 173 |
|
4 |
4, 14, 24, 34, 44 |
54, 64, 74, 84, 94 |
104, 114, 124, 134 |
144, 154, 164, 174 |
|
5 |
5, 15, 25, 35, 45 |
55, 65, 75, 85, 95 |
105, 115, 125, 135 |
145, 155, 165, 175 |
|
6 |
6, 16, 26, 36, 46 |
56, 66, 76, 86, 96 |
106, 116, 126, 136 |
146, 156, 166, 176 |
|
7 |
7, 17, 27, 37, 47 |
57, 67, 77, 87, 97 |
107, 117, 127, 137 |
147, 157, 167, 177 |
|
8 |
8, 18, 28, 38, 48 |
58, 68, 78, 88, 98 |
108, 118, 128, 138 |
148, 158, 168, 178 |
|
9 |
9, 19, 29, 39, 49 |
59, 69, 79, 89, 99 |
109, 119, 129, 139 |
149, 159, 169, 179 |
|
10 |
10, 20, 30, 40, 50 |
60, 70, 80, 90, 100 |
110, 120, 130, 140 |
150, 160, 170, 180 |
2. При двух контрольных работах по учебному плану:
-
Номера задач для контрольных заданий
№
1
2
1
1, 21, 31, 41, 51, 61, 81
101, 111, 131, 141, 151, 161
2
2, 22, 32, 42, 52, 62, 82
102, 112, 132, 142, 152, 162
3
3, 23, 33, 43, 53, 63, 83
103, 113, 133, 143, 153, 163
4
4, 24, 34, 44, 54, 64, 84
104, 114, 134, 144, 154, 164
5
5, 25, 35, 45, 55, 65, 85
105, 115, 135, 145, 155, 165
6
6, 26, 36, 46, 56, 66, 86
106, 116, 136, 146, 156, 166
7
7, 27, 37, 47, 57, 67, 87
107, 117, 137, 147, 157, 167
8
8, 28, 38, 48, 58, 68, 88
108, 118, 138, 148, 158, 168
9
9, 29, 39, 49, 59, 69, 89
109, 119, 139, 149, 159, 169
10
10, 30, 40, 50, 60, 70, 90
110, 120, 140, 150, 160, 170
Рабочая программа курса "Высшая математика"
Рабочая программа рассчитана на 180 учебных часов, содержит перечисление тем. которые должны быть изучены студентами. Последовательность изучения тем, методика их изложения и распределение по семестрам устанавливается с учетом потребностей специальных и смежных кафедр.
Содержание программы.
ТЕМА 1. Элементы линейной алгебры.
Определители второго и третьего порядков и их свойства. Миноры и алгебраические дополнения. Разложение определителя по элементам какого-либо ряда. Понятие об определителях n-го порядка.
Решение систем линейных уравнений с помощью определителей. Формулы Крамера. Метод Гаусса.
Матрицы. Действия над матрицами. Обратная матрица. Матричная запись системы линейных уравнений и ее решение с помощью обратной матрицы.
Ранг матрицы. Основные теоремы о ранге. Вычисление ранга матрицы. Произвольные системы линейных уравнений. Теорема Кронекера-Капелли.
Жордановы исключения. Применения Жордановых исключений в линейной алгебре. Базисные и свободные переменные. Базисные решения. Метод Гаусса-Жордана
Метод полного исключения переменных. Нахождение базисных решений системы линейных уравнений. Неотрицательные базисные решения системы линейных уравнений.
1.7 Понятие собственных чисел и собственных векторов матриц. Методы их нахождения.
1.8 Понятие квадратичной формы. Положительно определенные квадратичные формы. Условия Сильвестра. Приведение квадратичной формы к каноническому виду.
ТЕМА 2. Элементы аналитической геометрии и векторной алгебры.
2.1 Системы координат на прямой. плоскости. в пространстве. Основные задачи на метод координат (расстояние между двумя точками, деление отрезка в данном отношении).
2.2 Понятие об уравнении линии. Уравнение прямой с угловым коэффициентом. через точку в заданном направлении, через две точки. Общее уравнение прямой. Угол между двумя прямыми; условия параллельности и перпендикулярности двух прямых. Расстояние от точки до прямой.
2.3 Канонические уравнения кривых второго порядка; окружности, эллипса, гиперболы, параболы.
2.4 Векторы. Сложение и вычитание векторов. Умножение вектора на число. Длина вектора. Угол между векторами. Проекция вектора на оси. Координаты вектора. Скалярное произведение векторов.
2.5 Разложение вектора по системе векторов. Линейно зависимые и линейно независимые системы векторов. Базис системы векторов. Многомерные векторы. действия с ними. Ортогональные системы векторов. Переход от одного базиса к другому.
2.6 Плоскость. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение плоскости, его исследование, понятие гиперплоскости.
2.7 Неравенства первой степени на плоскости и их геометрический смысл. Решение линейных неравенств на плоскости и в пространстве.
Тема 3.Введение в математический анализ.
3.1.Определение функции. Область определения функции; способы ее задания.
Графическое изображение функции. Понятия о неявной. обратной. сложной функции. условия ее существования. Основные элементарные функции.
3.2 Числовая последовательность и ее предел. Предел функции. Односторонние пределы. Бесконечно малые и бесконечно большие функции, их свойства. Основные теоремы о пределах. Первый и второй замечательные пределы.
3.3 Непрерывность функции в точке и на интервале. Использование непрерывности для вычисления пределов. Раскрытие неопределенных выражений. Точки разрыва функции. Типы разрывов, их классификация. Непрерывность основных элементарных функций. Свойства функций. непрерывных на отрезке. Сравнение бесконечно малых функций и их эквивалентность. Использование эквивалентности для вычисления пределов.
ТЕМА 4. Дифференциальное исчисление функций одной переменной, его использование для исследования функций.
4.1 Производная функции, ее геометрический и механический смысл. Основные теоремы о производной. Производные основных элементарных функций. Производная сложной функции. Производная обратной и неявной функции. Производные высших порядков. Применения понятия производной в экономике.
4.2 Дифференциал функции; его геометрический смысл. Свойства дифференциала. Применение дифференциала в приближенных вычислениях.
4.3 Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа, Коши. Правило Лопиталя. Точки экстремума. Необходимые и достаточные условия существования экстремума.
4.4 Исследование с помощью производных функций на выпуклость и вогнутость Точки перегиба. Асимптоты кривой. Схема исследования функции и построение графика. Использование выпуклого анализа функций в экономических вопросах.
ТЕМА 5. Дифференциальное исчисление функций нескольких независимых переменных.
5.1 Определение функции нескольких независимых переменных. Область определения. Предел и непрерывность функции нескольких независимых переменных. Частные производные первого порядка. Понятие о частных производных высших порядков.
5.2. Полный дифференциал функции нескольких независимых переменных; его применение в приближенных вычислениях. Производная в данном направлении. Градиент функции, его свойства, использование при решении экономических задач.
5.3.Экстремум функции многих переменных. Необходимое условие. Понятие о достаточных условиях экстремума функций от двух независимых переменных. Условный экстремум. Примеры экономических задач.
5.4.Задача обработки наблюдений. Подбор параметров кривых по способу наименьших квадратов.
5.5. Неявные функции. Производные от неявных функций.
ТЕМА 6.Неопределенный интеграл.
6.1.Неопределенный интеграл; его свойства. Таблица основных интегралов. Основные методы интегрирования.
6.2.Интегрирование рациональных дробей с квадратичными знаменателями. Интегрирование рациональных дробей методом разложения на элементарные дроби.
6.3.Интегрирование простейших иррациональностей. Интегрирование некоторых тригонометрических выражений.
ТЕМА 7.Определенный интеграл.
7.1 Задачи. приводящие к понятию определенного интеграла. Определенный интеграл как предел интегральных сумм. Свойства определенного интеграла.
7.2 Производная от определенного интеграла по верхнему пределу. Связь между определенным и неопределенным интегралом (формула Ньютона-Лейбница). Вычисления определенных интегралов способом подстановки и по частям.
7.3 Геометрические приложения определенного интеграла: вычисление площадей криволинейных фигур и объемов тел вращения. Приближенное вычисление определенных интегралов по формулам прямоугольников. трапеций Симпсона.
7.4 Несобственные интегралы:
-интегралы с бесконечными пределами интегрирования.
-интегралы от неограниченных функций.
7.5 Понятие о двойном интеграле. Сведение двойного интеграла к повторному.
ТЕМА 8.Дифференциальные уравнения.
8.1 Понятие о дифференциальном уравнении и его решении. Задача Коши. Решение дифференциальных уравнений первого порядка с разделяющимися переменными. однородных и линейных.
Решение линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэфициентами и с правыми частями специального вида: f(x)=Pn(x)*eax; f(x)=eax(Acos Bx+Bsin Bx)
Системы линейных дифференциальных уравнений с постоянными коэффициентами. Понятие об устойчивости решений.
Линейные разностные уравнения с постоянными коэффициентами.
Тема 9.Ряды.
9.1 Понятие числового ряда. Сходимость рядов. Свойства сходящихся рядов. Необходимое условие сходимости. Ряд геометрической прогрессии.
9.2 Признаки сходимости рядов с положительными членами – признак Даламбера, Коши (радикальный и интегральный), признаки сравнения.
9.3 Знакопеременные ряды. Абсолютная и условная сходимости. Теорема Лейбницк.
9.4 Степенные ряды. Теорема Абеля. Радиус сходимости. Область сходимости степенного ряда. Разложение функций в степенной ряд.
Библиографический список
Кудрявцев В. А. .Демидович В. П. Краткий курс высшей математики. 6-е изд. М.: Наука.1985г.
Карасев А. И. .Аксютина Е. М. .Савельева Т. И. Курс высшей математики для экономических ВУЗов. М. :Высшая школа.ч1.ч2.1982г.
Минорский В. П. Сборник задач по высшей математике. М.:"Наука".1978г. М.: Высшая школа.1979г.
1. Яке число називається комплексним ?
а) числа виду
 ,
де
x
і
,
де
x
і
 –
дійсні числа,
називаються комплексними числами.
–
дійсні числа,
називаються комплексними числами.
б) числа виду

в) числа виду

2. Який вигляд має тригонометрична форма комплексного числа z?
а)
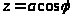
б)

в)

3.
 ;
;
 чому дорівнює
чому дорівнює

а)

б)

в)

4.
 .
Чому дорівнює z>1>6
?
.
Чому дорівнює z>1>6
?
а)

б)

в)

5. Як поділити комплексні числа задані в тригонометричній формі ?
а) треба модуль чисельника поділити на модуль знаменника, а аргументи додати;
б) треба модуль чисельника помножити на модуль знаменника, а від аргумента чисельника відняти аргумент знаменника;
в) треба модуль чисельника поділити на модуль знаменника, а від аргумента чисельника відняти аргумент знаменника;
6. Що називається об’єднанням двох множин A і B ?
а) об’єднанням двох множин A та B називається множина, яка складається із тих елементів що належать одночасно обом множинам;
б) об’єднанням множин A та B називається множина, яка складається із тих і тільки тих елементів, які містяться хоча би в одній із множин A або B;
в) об’єднанням двох множин A і B називається множина, яка складається із тих і тільки тих елементів, які належать А але не належать В.
7. Що називається висловлюванням ?
а) Висловлюванням називається всяке речення;
б) Висловлюванням називається всяке твердження, про яке можна сказати чи воно істинне чи хибне;
в) Висловлюванням називається деяка сукупність об’єктів, об’єднанних в одну групу за якоюсь ознакою.
8. Які логічні операції ілюструють паралельне та послідовне з’єднання контактів електричного кола ?
а) імплікація;
б) заперечення;
в) диз’юнкція та кон’юнкція.
9. Що називається
границею функції
 в точці
в точці
 ?
?
а) число
 називається границею функції
називається границею функції
 в точці
в точці
 якщо для всякого
якщо для всякого
 знайдеться таке
знайдеться таке
 ,
що як тільки
,
що як тільки



б) число
 називається границею функції
називається границею функції
 в точці
в точці
 ,
якщо при
,
якщо при


в) число
 називається границею функції
називається границею функції
 в точці
в точці
 ,
якщо
,
якщо
 .
.
10. В
якому випадку функція
 називається нескінчено малою в точці
називається нескінчено малою в точці
 ?
?
а) якщо
 ;
;
б) якщо
 ;
;
в) якщо
 .
.
11. В якому випадку
функція
 називається нескінченно великою в точці
називається нескінченно великою в точці
 ?
?
а) якщо
 ;
;
б) якщо
 ;
;
в) якщо
 .
.
12. Чому дорівнює границя відношення сінуса аргумента до аргумента при прямуванні аргумента до нуля ?
а)
 ;
;
б)
 ;
;
в)
 .
.
13. Чому дорівнює
 ?
?
а)
 ;
;
б)
 ;
;
в)
 .
.
14. Функція
 визначена в точці
визначена в точці
 і її границя в цій точці дорівнює значенню
функції в цій точці
і її границя в цій точці дорівнює значенню
функції в цій точці
 .
Як називається така функція ?
.
Як називається така функція ?
а) неперервною;
б) диференційованою;
в) інтегрованою.
15. Що таке похідна
функції
 ?
?
а) це відношення приросту функції до приросту аргументу;
б) це відношення приросту аргумента до приросту функції;
в) це границя відношення приросту функції до приросту аргумента при умові, що приріст аргумента прямує до нуля.
16. Який механічний зміст похідної ?
а) це швидкість зміни функції;
б) це кутовий коефіцієнт дотичної;
в) це прискорення.
17. Як обчислюється
похідна складної функції
 ,
,
 ?
?
а)
 ;
;
б)
 ;
;
в)
 .
.
18. Функція
 диференційована в точці
диференційована в точці
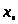 .
Чи буде вона неперервною в цій точці ?
.
Чи буде вона неперервною в цій точці ?
а) не буде;
б) залежить від вигляду функції;
в) якщо функція
диференційована в точці
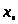 ,
то вона в ній і неперервна.
,
то вона в ній і неперервна.
19. Що таке диференціал
функції
 ?
?
а) диференціал функції
– це головна частина приросту функції,
лінійна відносно
 ;
;
б) диференціал функції – це приріст функції;
в) диференціал функції – це різниця між двома послідовними значеннями аргумента функції.
20. Для розкриття невизначеностей яких видів можна користуватись правилом Лопіталя ?
а)
 ; б)
; б)
 ;
;
 ; в)
; в)
 .
.
21. Похідна функції на
інтервалі
 додатня. Що можна сказати про поведінку
функції на
додатня. Що можна сказати про поведінку
функції на
 ?
?
а) функція зростає;
б) функція спадає;
в) функція стала.
22. Функція зростає на
 .
Що можна сказати про похідну функції
на
.
Що можна сказати про похідну функції
на
 ?
?
а) похідна від’ємна;
б) похідна дорівнює нулю;
в) похідна додатня.
23. Функція
 в точці
в точці
 має екстремум. Що можна сказати про
значення її похідної в цій точці ?
має екстремум. Що можна сказати про
значення її похідної в цій точці ?
а)
 ;
;
б)
 або
або
 не існує;
не існує;
в)
 .
.
24.
 і при переході через цю точку змінює
свій знак з + на - .Що можна сказати про
значення функції
і при переході через цю точку змінює
свій знак з + на - .Що можна сказати про
значення функції
 ?
?
а) функція в точці
 має max;
має max;
б) функція в точці
 має min;
має min;
в) функція в точці
 від’ємна.
від’ємна.
25. На проміжку

 .
Яким буде графік функції на цьому
проміжку ?
.
Яким буде графік функції на цьому
проміжку ?
а) графік функції опуклий;
б) функція зростає;
в) графік функції угнутий.
26. Графік функції на
 опуклий. Що можна сказати про значення
другої похідної на цьому проміжку ?
опуклий. Що можна сказати про значення
другої похідної на цьому проміжку ?
а)
 ;
;
б)
 ;
;
в)
 .
.
27.
 .
Чи має ця функція асимптоту і яку ?
.
Чи має ця функція асимптоту і яку ?
а)
 - похила асимптота;
- похила асимптота;
б)
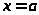 - вертикальна асимптота;
- вертикальна асимптота;
в)
 - горизонтальна асимптота.
- горизонтальна асимптота.
28. Які умови повинні
виконуватись, щоб функція
 мала похилу асимптоту
мала похилу асимптоту
 ?
?
а) повинна існувати
границя
 ;
;
б) повинна існувати
границя
 ;
;
в) повинні одночасно
існувати границі
 і
і

29. Що називається векторною функцією скалярного аргумента t ?
а) змінний вектор
 називається векторною функцією скалярного
аргумента;
називається векторною функцією скалярного
аргумента;
б)
 ;
;
в)
 .
.
30. Яким рівнянням
задається дотична до кривої в просторі
заданої за допомогою рівнянь
 в точці, що відповідає значенню
в точці, що відповідає значенню
 ?
?
а)

б)
 ;
;
в)
 ;
;
31. Яка функція називається
первісною для функції
 ?
?
а) - це функція
 ,
похідна від якої дорівнює
,
похідна від якої дорівнює
 ;
;
б) - це функція
 ,
яка дорівнює
,
яка дорівнює
 ;
;
в) - це функція
 ,
яка дорівнює
,
яка дорівнює
 .
.
32. Записати первісну
 функції
функції

а)
 ;
;
б)
 ;
;
в)
 .
.
33. Записати первісну
 функції
функції

а)
 ;
;
б)
 ;
;
в)
 .
.
34. В чому полягає універсальна тригонометрична підстановка ?
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
35. Як визначається визначений інтеграл ?
а)
 ;
;
б)
 ;
;
в)
 .
.
36. Укажіть формулу Ньютона – Лейбніца.
а)
 ;
;
б)
 ;
;
в)
 .
.
37. Чому дорівнює
 ?
?
а)
 ; б)
; б)
 ;
;
в)
 .
.
38. Укажіть формулу Сімпсона.
а)
 ;
;
б)
 ;
;
в)
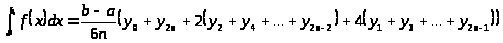 .
.
 1
1