Определение вероятности
КОНТРОЛЬНАЯ РАБОТА № 11
ВАРИАНТ 8
1. В ящике 10 деталей, среди которых 3 бракованных. Случайно извлекли 4 детали. Найти вероятность того, что среди них окажутся две бракованных.
Будем использовать классическое определение вероятности.
Четыре детали из десяти можно выбрать
способами (число сочетаний из десяти
элементов по четыре). Поэтому n
— число равновозможных событий равно
т.к.
Две бракованных детали из трех можно
выбрать
способами:
Две стандартных детали из семи можно
выбрать
способами:
,
поэтому m — число
благоприятных событий равно
.
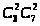2. ОТК проверяет изделие на стандартность. Вероятность стандартности изделия равна 0,85. Найти вероятность того, что из двух проверенных изделий только одно стандартно. Ответ записать в виде десятичной дроби.
Введем события
— первое проверенное изделие стандартное,
— второе проверенное изделие стандартное,
— первое проверенное изделие нестандартное,
— второе изделие нестандартное,
— из двух проверенных изделий только
одно стандартное. Тогда
.
События
несовместимы, поэтому по правилу сложения
вероятностей
,
получаем:
,
т.к. события
и
— независимы, то
.
По условию:
Получаем:
3. Три стрелка А, В, С стреляют по некоторой цели, делая не более одного выстрела. Вероятности попадания их при одном выстреле соответственно равны 0,7, 0,8, 0,9. Стрельбу начинает А. Если он промахнется, то стреляет в. Если и В промахнется, то стреляет С. Найти вероятность (в виде десятичной дроби) того, что цель будет поражена.
Пусть событие
— цель поражена, гипотезы:
— первый стрелок попал в цель,
— первый стрелок промахнулся, второй
попал,
— первый промахнулся, второй промахнулся,
третий попал.
Вероятность события
:
.
По формуле умножения вероятностей (
учитывая, что вероятности промаха
стрелками равен соответственно
).
По формуле сложения вероятностей получим:
4. При рентгеновском обследовании вероятность обнаружить туберкулез равна 0,9. Вероятность принять здорового человека за больного равна 0,01. Доля больных туберкулезом ко всему населению равна 0,001. Найти вероятность того, что человек здоров, хотя он признан больным при обследовании. Ответ округлить до 0,001.
По формуле умножения вероятностей:
В нашем случае
Искомая вероятность:
5.Стрельба продолжается до первого
попадания, но не более 4-х выстрелов.
Вероятность попадания при каждом
выстреле равна 0,6. Х – число израсходованных
патронов. Найти (ответы вводить в виде
десятичной дроби): а) ряд распределения
Х; б) функцию распределения F (х), в ответ
записать F (1,5), F (3,5); в)
;
г)
,
ответ округлить до 0,01; д)
.
а) Случайная величина Х может принимать
значения (1, 2, 3, 4). Найдем вероятности
этих значений, используя правило
умножения вероятностей
(промах при первом выстреле, попадание
при втором),
(промахи при первых двух выстрелах,
попадание при третьем),
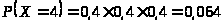(первые три выстрела — промах).
Запишем ряд распределения Х:
-
Х
1
2
3
4
Р
0,6
0,24
0,096
0,064
б) Функцию распределения
найдем, пользуясь соотношением:
,
где
,
получаем:
в) Математическое ожидание
дискретной случайной величины найдем
по формуле:
г) Дисперсию случайной величины
найдем по формуле:
д) Искомую вероятность того, что случайная
величина Х примет значение
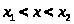найдем по формуле:
,
т.е.
6. Дана плотность распределения случайной величины Х:
Найти: а) константу А; б) функцию
распределения
,
в ответ записать
F(3); в)
;
г)
,
; д)
а) Из условия нормировки
следует, что
,
откуда
,
т.е.
.
б) Воспользуемся формулой
Если
,
поэтому
,
при
.
Если
,
.
Получаем:
в) Применяем формулу:
г) Применяем формулу:
д) Применим формулу:
7. Деталь, изготовленная автоматом, считается годной, если отклонение Х ее контролируемого размера от номинала не превышает 18 мм. Величина Х распределена нормально, причем σ х =9 мм. Найти вероятность того, что деталь будет признана годной. Ответ округлить до 0,01.
Применим формулу:
где
Δ — допустимое отклонение;
σ — среднее квадратическое отклонение,
эта
функция табулирована, ее значение берем
из таблицы.
Получаем:
.
Из таблицы находим
.
КОНТРОЛЬНАЯ РАБОТА № 12
ВАРИАНТ 8
1. Дана матрица распределения вероятностей системы (X,Y)
-
Х
Y
-1
0
3
2
0,11
0,25
0,14
3
0,12
0,20
0,18
Найти: а) ряды распределений X и Y; б)
;
в)
;
г)
;
д)
;
е)
;
ж)
,
округлить до 0,01; з) ряд распределения
Y, если X = 0; и)
,
округлить до 0,01.
а) Суммируя по столбцам, а затем по столбцам элементы матрицы распределения, получаем искомые ряды распределения.
-
Х
-1
0
3
Р
0,23
0,45
0,32
Y
2
3
Р
0,5
0,5
б) Используем формулу:
в)
.
г) Используем формулу:
д)
.
е) Используем формулу:
ж)
.
Вычитаем по формуле:
з) Используем формулу:
Получаем ряд распределения:
-
2
3
Р
и)
2. Дана плотность распределения вероятностей системы (X, Y)
Найти: а) константу
С; б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
;
и) F(2,10); к)
а) Константу С найдем из условия нормировки:
Найдем уравнение прямой ОВ:
Получим:
б) Используем формулы:
,
если x<0 или x>4,
если 0<x<4
,
если у<0 или y>1, если
0<y<1, то:
в) По формуле
получаем:
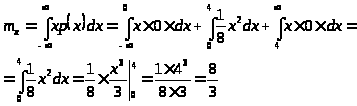
г)
.
д)
е)
ж)
.
,
где D — область, лежащая внутри треугольника ОАВ
з)
.
и)
,
где D — треугольник ОСD:
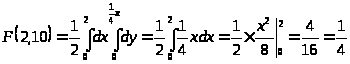
к)
При
величина x меняется
равномерно от
до
,
поэтому
3. По данным выборки объема n = 12 нормально
распределенной случайной величины Х
найдена исправленная дисперсия s = 5,1.
Найти доверительный интервал, содержащий
среднее квадратичное отклонение
величины Х с вероятностью 0,99. В ответ
ввести координату правого конца
интервала.
Найдем исправленное среднее квадратическое отклонение S’:
Доверительный интервал ищем в виде:
или
в зависимости от величины q,
которое находим из таблицы.
При n=12, γ=0,99 находим q=0,9, следовательно, т.к. q<1 доверительный интервал ищем в виде
.
или
