Экстремальная задача на индексационных классах
Содержание
Введение
Глава 1. Неравенство Маркова на индексационных классах
§ 1. Экстремальная задача
§ 2. Свойства отображения

§ 3. Доказательство теоремы
Глава 2. О чебышевской экстремальной задаче на [0, )
Литература
Введение
В работе вводится понятие индекса функции на [0,) относительно произвольного класса F функций на [0, ), основанное на сравнении двух функций через количество перемен знака их разности. С помощью понятия индекса аксиоматически определяется индексационный класс F. На индексационных классах изучается конечная проблема моментов.
Определение 1. Скажем, что функция (t), tR1, имеет k строгих перемен знака, если существуют множества A>1><A>2><…<A>k>>+1>, такие, что
а)
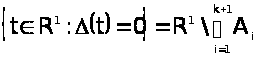 ;
;
б) знаки функции (t) на множествах A>1>, A>2>, …, A>k>>+1> перемежаются.
Пусть f(t)
и g(t)
– функции на R1.
Пишем
 ,
если функция =g-f
имеет k-1
строгих перемен знака, причем на последнем
множестве строгого знакопостоянства
она отрицательна.
,
если функция =g-f
имеет k-1
строгих перемен знака, причем на последнем
множестве строгого знакопостоянства
она отрицательна.
Нетрудно видеть, что
отношение
 выполнено тогда и только тогда, когда
выполнено тогда и только тогда, когда
а) не существует точки x>1>, …, x>k> (-<x>1><…<x>k><) такие, что
(-1)k-i
f(x>i>)
> (-1)k-i
g(x>i>),
 ;
;
б) существуют точки y>1>, …, y>k> (-<y>1><…<y>k><) такие, что
(-1)k-i
f(y>i>)
> (-1)k-i
g(y>i>),
 .
.
Пусть F – некоторый класс непрерывных слева функций на [0, ) и f, g F.
Определение 2. Пишем
 ,
если для любой функции hF,
hg,
выполнено одно из отношений:
,
если для любой функции hF,
hg,
выполнено одно из отношений:
 ,
,
 ,
,
 ,
,
 .
Пишем
.
Пишем
 ,
если для любой функции hF,
hf,
выполнено одно из отношений:
,
если для любой функции hF,
hf,
выполнено одно из отношений:
 ,
,
 ,
, ,
,
 .
.
Функция f
имеет индекс k-
в F,
если выполнено отношение
 и не выполнено
и не выполнено
 .
Функция g
имеет индекс k+
в F,
если выполнено
.
Функция g
имеет индекс k+
в F,
если выполнено
 и не выполнено
и не выполнено
 .
.
Через I>k>- (I>k>+), k1, обозначим совокупность всех функций с индексом k- (k+) в F.
Пусть U – семейство функций на [0, ).
Через F>U> обозначим множество функций fF, для которых интегралы
 ,
uU,
,
uU,
абсолютно сходятся.
В случае
 положим
положим
 ,
fF>U>,
AF>U>,
,
fF>U>,
AF>U>,
 :
:
> >,
F>i>(A)={F>i>(f):
fA},
>,
F>i>(A)={F>i>(f):
fA},
 ,
,
 ,
,
 .
.
Множество
 называется моментным пространством
класса F
относительно системы функций
называется моментным пространством
класса F
относительно системы функций
 .
.
Лемма 1. Пусть системы
u>1>(t),
…, u>n>(t)
и u>1>(t),
…, u>n>(t),
u>n>>+1>(t)
образуют T>+>-системы
на [0, )
такие, что
 .
Тогда отношение
.
Тогда отношение
 невозможно для
невозможно для
 и, если
и, если
 ,
то
,
то
 .
.
Доказательство.
Допустим, что
 ,
где kn,
и A>1>,
…, A>k>
– множества строгого знакопостоянства
функции g
- f.
Для векторов
,
где kn,
и A>1>,
…, A>k>
– множества строгого знакопостоянства
функции g
- f.
Для векторов
 рассмотрим матрицу
рассмотрим матрицу
 .
.
Так как
 ,
,
 ,
,
то есть
 ,
(1)
,
(1)
где d>i>(-1)k-i,
 и d>i>=0,
и d>i>=0,
 для всех векторов
для всех векторов
 .
.
Из (1) следует, что
detH( )=0
для любых
)=0
для любых
 .
С другой стороны, применив k
раз теорему о среднем к H(
.
С другой стороны, применив k
раз теорему о среднем к H( ),
получим
),
получим
 ,
(2)
,
(2)
где 0>1><>2><…<>k><.
Так как векторы
 линейно зависимы, то их можно дополнить
до системы линейно независимых векторов
линейно зависимы, то их можно дополнить
до системы линейно независимых векторов

 .
Из (2) получаем
.
Из (2) получаем
 .
.
Пусть
теперь
 и
и
 .
.
Так как
 ,
(3)
,
(3)
где d>i>=(-1)n+1-i,
 ,
то
,
то
 ,
,
где H
– матрица, записанная в (3) слева,
 -
матрица, получаемая из H
удалением (n+1)-ых
строки и столбца. Применив теорему о
среднем, получаем detH>0,
-
матрица, получаемая из H
удалением (n+1)-ых
строки и столбца. Применив теорему о
среднем, получаем detH>0,
 .
Вместе с равенством d>n>>+1>=1
это означает, что d>0.
.
Вместе с равенством d>n>>+1>=1
это означает, что d>0.
Определение 3. Скажем,
что последовательность {f>i>}>i>>>>1>
функций на [0, )
относительно класса U
слабо сходится к функции f
 ,
если
,
если

для всех uU.
Определение 4.
Множество AF>U>
назовем (k,
U)
окрестностью функции f
в F,
если fA
и множество А имеет вид
 ,
где V
открыто,
,
где V
открыто,
 при
при
 ,
,
 при
при

 .
.
Множество AF>U> назовем (k, U)-открытым, если каждая функция fA имеет (k, U) окрестность, состоящую из функций множества А.
Определение 5. Класс F непрерывных слева, неотрицательных функций на [0, ) назовем нижним U-индексационным с дефектом n, если:
1. Класс F равномерно ограничен, то есть существует L>0, такое, что f(t)L при t0, fF;
2.
 ;
;
3. Множества I>k>- (k-1, U) – открыты для всех k>n+1;
4. Из любой последовательности {f>i>}>i>>>>1>I->k>>+1> (k>n) такой, что
 ,
,
можно выделить
подпоследовательность, слабо относительно
класса U
сходящуюся к некоторой функции
 .
.
Пусть система
 образует T>+>
- систему на [0, ).
образует T>+>
- систему на [0, ).
Рассмотрим систему
функций
 ,
такую, что w>i>=u>i>
для
,
такую, что w>i>=u>i>
для
 и
и
 - T>+>
- системы для mn
(см. [1]).
- T>+>
- системы для mn
(см. [1]).
Теорема 1. Пусть
система
 образует T>+>
- систему на [0, ),
F-нижний
W-индексационный
с дефектом n
класс функций на [0, ).
Тогда
образует T>+>
- систему на [0, ),
F-нижний
W-индексационный
с дефектом n
класс функций на [0, ).
Тогда
 .
.
Доказательство.
Пусть
 .
Согласно условию 2 определения
индексационного класса, существует
последовательность {f>j>}>j>>>>1>I>k>-
такая, что
.
Согласно условию 2 определения
индексационного класса, существует
последовательность {f>j>}>j>>>>1>I>k>-
такая, что
 .
Зафиксируем произвольное f>l>.
.
Зафиксируем произвольное f>l>.
Если f>l>I>k>-, где kn+1, то положим f>l>*=f>l>.
Пусть k>n+1
и ={ }
– (k-1,
W)
окрестность f>l>
в I>k>-.
}
– (k-1,
W)
окрестность f>l>
в I>k>-.
Рассмотрим произвольные
 и
и
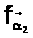
 .
Допустим, что
.
Допустим, что
 .
Согласно лемме 1, отношения
.
Согласно лемме 1, отношения
 и
и
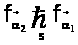 невозможны для sk-1.
Следовательно,
невозможны для sk-1.
Следовательно,
 и
и
 ,
что невозможно.
,
что невозможно.
Таким образом,
отображение
 непрерывно и взаимно однозначно. Из
принципа инвариативности области (см.
[3]) следует, что
непрерывно и взаимно однозначно. Из
принципа инвариативности области (см.
[3]) следует, что
 - открытое множество в Rk-1,
содержащее
- открытое множество в Rk-1,
содержащее
 .
.
Пусть
 ,
,
 и
и
 - многочлен по системе
- многочлен по системе
 ,
имеющий k-2
нулей x>1>,
…, x>k>>-2>.
Условие >k>>-1>=0
противоречит чебышевости системы
,
имеющий k-2
нулей x>1>,
…, x>k>>-2>.
Условие >k>>-1>=0
противоречит чебышевости системы
 .
Положим >k>>-1>>0.
Тогда (см. [5]) P(t)>0
при t>x>k>>-2>.
.
Положим >k>>-1>>0.
Тогда (см. [5]) P(t)>0
при t>x>k>>-2>.
Имеем
 ,
,
где c>l>i
– i-ая
компонента вектора
 ,
и, следовательно,
,
и, следовательно,
 .
.
Так как константа К не зависит от f, то m>l>> >>-.
Кроме того,
 .
.
Возьмем последовательность
 ,
такую, что
,
такую, что
F>k>>-1>(f>lp>)>F>k>>-1>(f>lq>)=m>l> при p<q и
 ,
,
Рассмотрим произвольные
f>lp>
и f>lq>,
где p<q.
Так как
 ,
то отношения
,
то отношения
 и
и
 невозможны для sk-2.
Отношения
невозможны для sk-2.
Отношения
 и
и
 невозможны, так как f>lp>,
f>lq>I>k>-.
Из леммы 1 получаем
невозможны, так как f>lp>,
f>lq>I>k>-.
Из леммы 1 получаем
 .
.
Так как
 ,
то найдется функция
,
то найдется функция
 ,
такая, что F>k>>-1>(f>l>’)=m>l>.
,
такая, что F>k>>-1>(f>l>’)=m>l>.
Отношение f>l>’I>k>-
невозможно, в силу определения числа
m>l>
и принципа инвариативности области.
Отношения f>l>’I>m>-
для m<k-1
невозможны, так как
 .
Следовательно
.
Следовательно
 .
.
Продолжая таким
образом, через k-n-2
шагов получим функцию
 ,
такую, что
,
такую, что
 .
Из условия
.
Из условия
 следует утверждение теоремы 1.
следует утверждение теоремы 1.
Замечание 1. Класс F непрерывных слева, неотрицательных функций на [0, ) назовем верхним U-индексационным с дефектом n, если:
1. Класс F равномерно ограничен;
2.
 ;
;
3. Множества I>k>+ (k-1, U) – открыты для всех k>n+1;
4. Для k>n из любой последовательности {f>i>}>i>>>>1>I>k>+ такой, что
 ,
,
можно выделить
подпоследовательность, относительно
класса U
слабо сходящуюся к некоторой функции
 ;
;
5. I>k>+F>U> для kn+1.
Теорема 2. Пусть
система
 образует T>+>-систему
на [0, ),
F-верхний
W-индексационный
с дефектом n
класс функций на [0, ).
Тогда
образует T>+>-систему
на [0, ),
F-верхний
W-индексационный
с дефектом n
класс функций на [0, ).
Тогда
 .
.
Определение 6. Систему
 непрерывных на [0, )
функций назовем T>+>1-системой,
если она является T>+>-системой,
и, кроме того, системы u>1>,
…, u>l>>-1>,
u>l>>+1>,
…, u>n>
также являются T>+>-системами
для
непрерывных на [0, )
функций назовем T>+>1-системой,
если она является T>+>-системой,
и, кроме того, системы u>1>,
…, u>l>>-1>,
u>l>>+1>,
…, u>n>
также являются T>+>-системами
для
 .
.
Лемма 2. Пусть
 -
T>+>1-система
на [0, ),
функции f
и g
таковы, что
-
T>+>1-система
на [0, ),
функции f
и g
таковы, что
(-1)n-i
F>i>(f)
(-1)n-i
F>i>(g),
 .
.
Тогда отношения
 ,
,
 и
и
 ,
,
 ,
невозможны.
,
невозможны.
Доказательство.
Допустим, что имеет место отношение
 и 1pn.
и 1pn.
Пусть x>1>,
…, x>p>>-1>
(-<x>1><…<x>p>>-1><)
– точки перемен знака функции
 ;
x>о>=-,
x>n>=;
;
x>о>=-,
x>n>=;
 .
Выберем точки x>n>>-1><x>n>>-2><…<x>p><x>p>>-1>
так, чтобы
.
Выберем точки x>n>>-1><x>n>>-2><…<x>p><x>p>>-1>
так, чтобы
 ,
,
 ,
,
 .
Рассмотрим систему равенств
.
Рассмотрим систему равенств
 ,
(4)
,
(4)
где h>i>=1.
Из условия
 следует, что h>n>=1.
С другой стороны, из (4) получаем
следует, что h>n>=1.
С другой стороны, из (4) получаем
 ,
,
где А – матрица,
записанная в (4) слева, A>n>i
– матрица, получаемая из А удалением
i-ой
строки и n-го
столбца. Так как
 -
T>+>1-система
на [0, ),
то detA>0,
detA>n>i>0,
-
T>+>1-система
на [0, ),
то detA>0,
detA>n>i>0,
 .
Следовательно, h>n>0.
Получили противоречие.
.
Следовательно, h>n>0.
Получили противоречие.
Случай
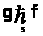 ,
,
 ,
рассматривается аналогично.
,
рассматривается аналогично.
Теорема 3. Пусть
 -
T>+>1-система
на [0, ),
F-нижний
W-индексационный
с дефектом n
класс функций на [0, ).
Тогда
-
T>+>1-система
на [0, ),
F-нижний
W-индексационный
с дефектом n
класс функций на [0, ).
Тогда
 .
.
Доказательство.
Пусть
 .
Возьмем последовательность векторов
.
Возьмем последовательность векторов
 так, чтобы
так, чтобы
 при
при
 и
и

для
 ,
j1.
,
j1.
Согласно теореме 1,
для любого
 найдется последовательность
найдется последовательность
 такая, что
такая, что
 .
.
Существует j>1>,
такое, что
 ,
где
- какая-либо метрика в Rn,
и
,
где
- какая-либо метрика в Rn,
и
 ,
,
 .
.
Выберем j>2>
так, чтобы
 и
и
 ,
,
 .
.
Продолжая таким
образом, получим последовательность
 такую, что
такую, что
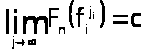 и
и
 (5)
(5)
Рассмотрим произвольные
 и
и
 .
Отношения
.
Отношения
 и
и
 для
k>n
невозможны, в силу условий
для
k>n
невозможны, в силу условий
 .
.
Из неравенств (5), в силу леммы 2, имеем
 ,
,
т. е. существует
функция
 такая, что
такая, что
 .
Включение
.
Включение
 противоречит условию
противоречит условию
 ,
в силу принципа инвариативности области.
,
в силу принципа инвариативности области.
Из
произвольности
 следует утверждение теоремы 2.
следует утверждение теоремы 2.
Глава 1 Неравенство Маркова на индексационных классах
§ 1 Экстремальная задача
Пусть
– некоторый класс функций распределения
(ФР) на [a,
b],
-<a<b<;
(t)
– (n+1)
раз непрерывно дифференцируемая функция
на [a,
b],
причем (k)(t)>0
для t[a,
b]
и
 ;
c>1>,
…, c>n>
– вещественные константы; [a,
b].
;
c>1>,
…, c>n>
– вещественные константы; [a,
b].
Экстремальная задача. Найти супремум и инфимум интеграла

на множестве

 ФР из ,
удовлетворяющих ограничениям
ФР из ,
удовлетворяющих ограничениям
 ,
,
 .
.
Для классов >o>
- всех ФР на [a,
b]
и В>L>
– ФР на [a,
b],
удовлетворяющих условию
 ,
-<x<y<,
задача решена в [1].
,
-<x<y<,
задача решена в [1].
Важность решение экстремальных задач на разных классах ФР обоснована, например, в [1 - 5].
Задача при b решена в [4] для мажоризационных классов.
Анализ задачи на мажоризационных классах в общем случае наталкивается на трудности. Выход мы видим в рассмотрении классов с иной структурой – индексационных классов ФР.
Ниже предполагается, что - индексационный с дефектом n класс ФР на [a, b]. Определение индексационного с дефектом n класса приведено в [5]. Индексационными являются многие важные классы ФР, например, >o>, B>L>, класс унимодальных ФР на [a, b] и др.
Обозначим (k
A,
):
I>k>+
(I>k>-)
–множество всех ФР из ,
имеющих индекс k+
(k-);
 ;
;
 - пространство моментов порядка k;
- пространство моментов порядка k;
 ;
;
 ;
;
 ,
,
 .
.
Основной результат работы содержится в утверждении.
Теорема.
Пусть
 ,
,
 .
Тогда:
.
Тогда:
 ,
,

 ,
,
 ,
,
 .
.
§ 2
Свойства отображения

Нам понадобятся два факта из [6].
1. Для любого
 существует и единственная ФР
существует и единственная ФР
 .
.
2. Если
 ,
то множество
,
то множество
 одноэлементно. Если
одноэлементно. Если
 ,
то существуют непрерывные, однопараметрические
семейства
,
то существуют непрерывные, однопараметрические
семейства
 (т. е.
(т. е.
 при
при
 и
и
 (значок
обозначает слабую сходимость)) и
(значок
обозначает слабую сходимость)) и
 ФР такие, что
ФР такие, что
 ,
, ,
,
 ,
для
и
,
для
и
 для .
для .
Пусть
 и
и
 ,
где
,
где
 ,
a,
b.
,
a,
b.
Функция >> непрерывна слева на [a, b] и >>(a)=0 для всех . Так как t>0 при t[a, b], то >> не убывает по .
Далее, из >k>
при k
следует

 >>.
Следовательно, семейства распределений
{
>>.
Следовательно, семейства распределений
{ }
и {
}
и { }
непрерывны.
}
непрерывны.
Определение 1. Функция
f
имеет на [a,
b]
m
строгих перемен знака, если существуют
множества B>0>(f)<…<B>m>(f)
(под X<Y
(X,
YR1)
понимаем x<y
для всех xX,
yY)
из [a,
b]
такие, что (-1)j
f(x)>0
(или (-1)j+1f(x)>0
при xB>j>(f),
 и f(x)=0
при
и f(x)=0
при
 .
.
Лемма 1. Для любого
распределения  (
( )
и для любого >>,
)
и для любого >>,
 ,
функция >>
- >
,
функция >>
- > >(>>
-
>(>>
-  )
имеет либо n+1,
либо n+2
строгих перемен знака на [a,
b].
)
имеет либо n+1,
либо n+2
строгих перемен знака на [a,
b].
Доказательство.
Предположим, что функция >>
-  имеет
более n+2
строгих перемен знака. Тогда существуют
a<x>0><x>1><…<x>n>>+3>b
такие, что (-1)i
[>>>
имеет
более n+2
строгих перемен знака. Тогда существуют
a<x>0><x>1><…<x>n>>+3>b
такие, что (-1)i
[>>> >
-
>
- ]
> 0,
]
> 0,
 .
Кроме того, >>(a)=
.
Кроме того, >>(a)= (a)=0.
Следовательно, существуют точки y>0>[a,
x>0>),
y>1>[x>0>,
x>1>),
…, y>n>>+3>[x>n>>+2>,
x>n>>+3>)
такие, что функция (-1)i
[t
- >>(t)]
возрастает в точке y>i>,
(a)=0.
Следовательно, существуют точки y>0>[a,
x>0>),
y>1>[x>0>,
x>1>),
…, y>n>>+3>[x>n>>+2>,
x>n>>+3>)
такие, что функция (-1)i
[t
- >>(t)]
возрастает в точке y>i>,
 ,
что противоречит условию
,
что противоречит условию
 .
.
Равенство
 запишем в виде
запишем в виде
 >>tc>i>,
>>tc>i>,
 ,
,
где
 ,
,
 ,
с>0>
= 1.
,
с>0>
= 1.
Очевидно, что
последовательности u>0>,
…, u>k>,
 ,
образуют T>+>
- системы на [a,
b].
Из условия (k)(t)>0
для t[a,
b]
и
,
образуют T>+>
- системы на [a,
b].
Из условия (k)(t)>0
для t[a,
b]
и
 следует (см. [1]), что последовательности
–u>0>,
…,-u>k>
следует (см. [1]), что последовательности
–u>0>,
…,-u>k>
 ,
также образуют T>+>
- системы. Следовательно, выполнены
условия мажоризационной теоремы (см.
[4]) и функция >>
- >
,
также образуют T>+>
- системы. Следовательно, выполнены
условия мажоризационной теоремы (см.
[4]) и функция >>
- > >не
может иметь n+1
строгих перемен знака.
>не
может иметь n+1
строгих перемен знака.
Пусть функция f(t) имеет k строгих перемен знака на [a, b]. Наряду с множествами B>i>(f) строгого знакопостоянства рассмотрим множества P>0>(f)=(-, infB>1>(f)], P>i>(f)=[supB>i>>-1>(f), infB>i>>+1>(f)],
 , P>k>(f)=[supB>k>>-1>(f),
+).
, P>k>(f)=[supB>k>>-1>(f),
+).
Зафиксируем ФР
 .
Рассмотрим два класса функций
.
Рассмотрим два класса функций
{>>>>
- > >:[0,1]}
и {>>>>
- >
>:[0,1]}
и {>>>>
- > >:[0,1]}.
>:[0,1]}.
Число (число ) назовем: параметром первого типа, если функция >> (>>) имеет n+2 строгих перемен знака (в этом случае на последнем множестве строго знакопостоянства функция >> (>>) отрицательна (положительна)); параметром второго типа, если функция >> (>>) имеет n+1 строгих перемен знака, причем на последнем множестве строгого знакопостоянства она отрицательна; параметром третьего типа, если функция >> (>>) имеет n+1 перемен знака, причем на последнем множестве строгого знакопостоянства она положительна.
Каждому [0,1] ([0,1]) сопоставим набор из n+3 множеств X>0>(), …, X>n>>+2>() (Y>0>(), …, Y>n>>+2>()) следующим образом. Если () есть:
параметр первого типа, то
X>i>()=P>i>(>>),
 (Y>i>()=P>i>(>>),
(Y>i>()=P>i>(>>),
 );
);
параметр второго типа, то
X>i>()=P>i-1>(>>),
 ,
X>0>()=(-,
infB>0>(>>)],
,
X>0>()=(-,
infB>0>(>>)],
(Y>i>()=P>i>(>>),
 ,
Y>n+2>()=(supB>n+1>(>>),
+));
,
Y>n+2>()=(supB>n+1>(>>),
+));
параметр третьего типа, то
X>i>()=P>i>(>>),
 ,
X>n>>+2>()=[supB>n>>+1>(>>),
+)),
,
X>n>>+2>()=[supB>n>>+1>(>>),
+)),
(Y>i>()=P>i>>-1>(>>),
 ,
Y>0>()=(-,
infB>0>(>>)]).
,
Y>0>()=(-,
infB>0>(>>)]).
Таким образом:
(-1)n-i>>(t)0
при
tIntX>i>(),
 ,
(1)
,
(1)
(-1)n-i>>(t)0
при
tIntY>i>(),
 .
.
При этом ни для какого i не существует интервала X, для которого выполнено строгое включение XIntX>i>() и (-1)n-i>>(t)0 при tX. Ни для какого i не существует интервала YIntY>i>() и (-1)n-i>>(t)0 при tY.
Заметим также, что X>i>(0)=Y>i>>+1>(0), X>i>>+1>(1)=Y>i>(1).
Определение 2. Отображение Z(): [0, 1]Z()R1 непрерывно, если из >i>0, x>i>x0, где 0, >i> [0, 1], x>i>Z(>i>), i1, следует x0Z(0).
Лемма 2. Отображения
X>i>(),
Y>i>(),
 непрерывны.
непрерывны.
Доказательство.
Пусть >j>,
j.
Обозначим через
 границы отрезка X>i>(>j>).
Определим a>0>=-.
Возьмем произвольную точку a>1>
сгущения последовательности {a>1>(j)}>j>>>>1>.
Пусть для удобства
границы отрезка X>i>(>j>).
Определим a>0>=-.
Возьмем произвольную точку a>1>
сгущения последовательности {a>1>(j)}>j>>>>1>.
Пусть для удобства
 .
Проделаем ту же операцию с последовательностями
{a>i>(j)}>j>>>>1>,
.
Проделаем ту же операцию с последовательностями
{a>i>(j)}>j>>>>1>,
 и {b>i>(j)}>j>>>>1>,
и {b>i>(j)}>j>>>>1>,
 .
Положим
b>n+2>=+.
.
Положим
b>n+2>=+.
Итак,
 ,
,
 ,
,
 (2)
(2)
причем -=a>0><a>1>b>0>a>2>b>1>…a>n+1>b>n>a>n+2>b>n+1><b>n+2>=+.
Из
(1) и (2) следует, что для
 .
.
(-1)n-i>>(t)0 (3)
при t(a>i>, b>i>), если a>i>b>i>.
Из (3) и
 следует, что a>i>b>i>,
следует, что a>i>b>i>,
 ,
так как в противном случае функция >>
имело бы не более n
строгих перемен знака, что противоречит
лемме 1. Отсюда и из определения X>i>()
следует [a>i>,
b>i>]X>i>(),
,
так как в противном случае функция >>
имело бы не более n
строгих перемен знака, что противоречит
лемме 1. Отсюда и из определения X>i>()
следует [a>i>,
b>i>]X>i>(), .
Для любого i
из x>j>[a>i>(j),
b>i>(j)]
и x>j>x0
вытекает, что x0[a>i>,
b>i>].
Следовательно, x0X>i>().
.
Для любого i
из x>j>[a>i>(j),
b>i>(j)]
и x>j>x0
вытекает, что x0[a>i>,
b>i>].
Следовательно, x0X>i>().
Непрерывность отображений Y>i>() доказывается аналогично.
§ 3 Доказательство теоремы
В случае
 утверждение
теоремы очевидно.
утверждение
теоремы очевидно.
Пусть
 .
.
Лемма 3. Для любого
ФР
 и любой точки [a,
b]
существует ФР
и любой точки [a,
b]
существует ФР
 такая, что >v>(t)>>(t)
(>v>(t)>>(t))
в некоторой окрестности точки .
такая, что >v>(t)>>(t)
(>v>(t)>>(t))
в некоторой окрестности точки .
Доказательство. Если
не существует такого i,
0in+2,
что n-1
четно и Y>i>(0),
то в некоторой окрестности точки
имеет место >0>0.
В этом случае положим
 .
.
Пусть существует i такое, что n-i четно и Y>i>(0).
Случай I,
in+2.
a)
Предположим, что Y>i>(1).
Пусть
 .
Согласно лемме 2, Y>i>().
В силу сделанного предположения, <1
и, следовательно, существует
последовательность {>j>}>j>>>>1>
такая, что Y>i>(>j>)
и >j>.
Пусть для некоторого >l>
не существует такого k,
что n-k
четно и Y>k>(>l>).
Тогда
.
Согласно лемме 2, Y>i>().
В силу сделанного предположения, <1
и, следовательно, существует
последовательность {>j>}>j>>>>1>
такая, что Y>i>(>j>)
и >j>.
Пусть для некоторого >l>
не существует такого k,
что n-k
четно и Y>k>(>l>).
Тогда
 в
некоторой окрестности точки .
В этом случае полагаем
в
некоторой окрестности точки .
В этом случае полагаем
 .
Если же для всех >j>,
j1,
существует k>j>
такие, что n-k>j>
четны и
.
Если же для всех >j>,
j1,
существует k>j>
такие, что n-k>j>
четны и
 ,
то существует m,
mi,
такое, что n-m
четно и Y>m>(>j>)
для бесконечного числа элементов
последовательности {>j>}.
По лемме 2 Y>m>().
Так как n-i
и n-m
четны, то mi-1,
mi+1.
Вместе с mi
это противоречит включению Y>i>().
,
то существует m,
mi,
такое, что n-m
четно и Y>m>(>j>)
для бесконечного числа элементов
последовательности {>j>}.
По лемме 2 Y>m>().
Так как n-i
и n-m
четны, то mi-1,
mi+1.
Вместе с mi
это противоречит включению Y>i>().
б) Предположим, что Y>i>(1)=X>i>>+1>(1). Пусть inf{X>i>>+1>()}. Согласно лемме 2, X>i>>+1>(). Если , то X>i>>+1>(0)=Y>i>>+2>(0). Это противоречит условию X>i>>+1>(). Поэтому и дальнейшее рассмотрение аналогично приведенному в а).
Случай II, i=n+2. а) При Y>n>>+2>(1) доказательство аналогично доказательству пункта а) случая I.
б) Пусть Y>n>>+2>(1).
Так как Y>n>>+2>(1)Y>n>>+1>(1),
то Y>n>>+1>(1).
Точка
не может совпадать с левым концом отрезка
Y>n>>+1>(1),
так как в этом случае множества Y>n>>+1>(1)
и Y>n>>+2>(1)
совпадают, что невозможно. Так как
Y>n>>+1>(1)
и не совпадает с левым концом отрезка
Y>n>>+1>(1),
то >1>(t)0
в некоторой окрестности точки .
В этом случае полагаем
 .
.
Итак, доказано
существование такой ФР
 ,
что >>->>
в некоторой окрестности точки .
Случай >>->>
рассматривается аналогично.
,
что >>->>
в некоторой окрестности точки .
Случай >>->>
рассматривается аналогично.
Теорема следует из леммы 3 и утверждения:
 >>()
и
>>()
и
 >>(+0)
достижимы. Докажем последнее.
>>(+0)
достижимы. Докажем последнее.
Пусть d= >>()
. Пусть последовательность ФР
>>()
. Пусть последовательность ФР
 ,
i,
такова, что
,
i,
такова, что  .
Выберем подпоследовательность
последовательности {>i>},
слабо сходящуюся к некоторой ФР
.
Выберем подпоследовательность
последовательности {>i>},
слабо сходящуюся к некоторой ФР
 . Покажем, что >>d.
Для произвольного >0
выберем <
такое, что >>->><
и -
точка непрерывности >>.
Существует номер N
такой, что для любого j>N
выполнено неравенство >
. Покажем, что >>d.
Для произвольного >0
выберем <
такое, что >>->><
и -
точка непрерывности >>.
Существует номер N
такой, что для любого j>N
выполнено неравенство > >()->>()<,
из которого следует, что >>()
- >
>()->>()<,
из которого следует, что >>()
- > >()<,
j>N.
Так как >
>()<,
j>N.
Так как > >()
>
>()
> >(),
то >>()
- >
>(),
то >>()
- > >()<,
откуда следует >>(
- d.
Последнее неравенство влечет >>d.
>()<,
откуда следует >>(
- d.
Последнее неравенство влечет >>d.
Глава 2 О чебышевской экстремальной задаче на [0, )
В настоящей работе на конкретных классах функций распределения (ФР) даны два подхода к решению чебышевской экстремальной задачи на [0, ).
Чебышевская экстремальная задача. Пусть - выпуклый класс ФР на [0, ), системы u>0>1 на [0, ) функций образуют T>+>-системы на [0, ).
Положим (1in, ):
 ,
,
 ,
,
 - моментное пространство класса
относительно системы
- моментное пространство класса
относительно системы
 .
.
Пусть
 .
.
Найти
 ,
где
,
где
 .
.
10. Первый подход заключается в урезании справа класса в точке x>0, наложении условий, при которых задача на «урезанном» классе >х> решается, и в переносе предельным переходом x решения на класс .
Для любого x>0 введем подкласс класса : >х>={:x+0)=1}.
Очевидно, для любых x>1><x>2>
 (1)
(1)
Предположим, что для любого x>0 >х >- индексационный с дефектом n класс ФР на [0, x] ([5]).
Примерами таких
классов служат: класс всех ФР на [0, ),
класс ФР вогнутых на [0, ),класс
ФР
на [0, ),
удовлетворяющих при 0x<y<
неравенству
 ,
L>0
и т. д.
,
L>0
и т. д.
Перечисленные выше классы являются нижними индексационными ([2]), т. е. для них выполнено включение
 (
( -замыкание
множества XRn),
-замыкание
множества XRn),
где I>i>- - множество всех ФР, имеющих индекс i- в .
Кроме того, для этих
классов справедливо включение
 ,
и следовательно,
,
и следовательно,
 (2)
(2)
Лемма 1.
 .
.
Доказательство.
Пусть
 .
Из выпуклости множества
.
Из выпуклости множества
 следует, что точка
следует, что точка
 является внутренней точкой некоторого
(n+1)-мерного
симплекса, лежащего в
является внутренней точкой некоторого
(n+1)-мерного
симплекса, лежащего в
 ,
т. е. существуют векторы
,
т. е. существуют векторы
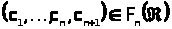 ,
и числа >>>0,
…, >n>>0,
>n>>+1>>0
такие, что
,
и числа >>>0,
…, >n>>0,
>n>>+1>>0
такие, что
 .
.
Из (2) следует
существование последовательностей
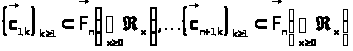 ,
таких, что
,
таких, что
 .
.
Тогда для достаточно больших k выполнено равенство
 ,
,
где
 ,
,
 .
.
Следовательно,
 .
.
Из леммы 1 следует,
что
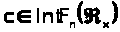 для достаточно больших x.
Так как класс >x>
является индексационным на [0, x],
то ([5])
для достаточно больших x.
Так как класс >x>
является индексационным на [0, x],
то ([5])
 ,
,
 ,
,
где
 ,
,
 (
( )
– ФР с нижним (верхним) индексом n+1
в классе >x>.
)
– ФР с нижним (верхним) индексом n+1
в классе >x>.
Так
как ФР
 имеет индекс (n+1)-
в
и
имеет индекс (n+1)-
в
и
 ,
то
,
то
 .
.
Из (1) следует, что
 .
.
Вид экстремальных
ФР
 и
и
 для рассматриваемых классов имеется в
[5].
для рассматриваемых классов имеется в
[5].
20. Второй подход продемонстрируем на примере класса >0> всех ФР на
Лемма 2. Если u>0>,
u>1>,
…, u>n>
– T>+>-система
на ,
то для всех i
и j
существуют пределы
 .
.
Доказательство. Из определения T>+>-системы следует, что для произвольных i, j и чисел функции u>j>(t) и u>j>(t)+u>j>(t) обращаются в нуль более, чем в n+1 точках.
Пусть х – наибольшее решение уравнения u>j>(t)=0. Рассмотрим уравнение
u>j>(t)+u>j>(t)=0, t>x. (3)
Уравнение
 (u>i>(t)0,
t>x)
имеет не более (n+1)
решений на (x,
)
при любых .
(u>i>(t)0,
t>x)
имеет не более (n+1)
решений на (x,
)
при любых .
Пусть
 ,
,
 .
.
Допустим, что
 не существует, т. е. А<B.
не существует, т. е. А<B.
Введем последовательности {t>i>}>i>>>>1>, {>i>}>i>>>>1>, удовлетворяющие условиям:
а) t>k>>k> при k;
б)
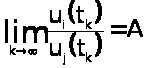 ,
,
 ;
;
в) t>1><>><t>2><>><…<t>m><>m><… .
Пусть c(A, B).
Из-за непрерывности
функции
 на (x,
)
уравнение
на (x,
)
уравнение

имеет бесконечное множество решений на (x, ).
Выберем 0j>0>n
так, чтобы
 для всех
для всех
 и обозначим
и обозначим
 .
.
Пусть число t>0>
таково, что
 при t>t>0>.
при t>t>0>.
Рассмотрим функцию

Пусть
 ,
,
 ,
,
 .
.
Легко видеть, что системы v>0>, v>1>, …, v>n> и v>0>, v>1>, …, v>n>, являются T>+>-системами на [0, ).
Предположим, что эти системы являются T>+>-системами также на [0, ], т. е. для любых 0t>0><t>1><…<t>n>>-1><t>n><
 ,
,
 ,
,
где
 .
.
Через
 обозначим множество ФР >0>,
для которых интегралы
обозначим множество ФР >0>,
для которых интегралы
 ,
,
 ,
абсолютно сходятся.
,
абсолютно сходятся.
Пусть
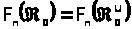 - моментное пространство класса
- моментное пространство класса
 относительно системы
относительно системы
 .
.
Рассмотрим класс
непрерывных слева и неубывающих на [0,
)
функций
 .
.
Имеем
 ,
т. е.
,
т. е.
 .
.
Заметим, что отображение
 является взаимно однозначным, причем
является взаимно однозначным, причем
 .
.
Таким образом,
 - множество всех неубывающих, непрерывных
слева функций ограниченной вариации
на [0, ).
- множество всех неубывающих, непрерывных
слева функций ограниченной вариации
на [0, ).
Пусть
 .
.
Необходимо найти
 .
(4)
.
(4)
Из равенств (>0>U)


следует, что задача (4) эквивалентна следующей.
Найти
 ,
(5)
,
(5)
где
 - множество функций
- множество функций
 ,
удовлетворяющих равенствам
,
удовлетворяющих равенствам
 ,
,
 ,
,
 .
.
Таким образом, задача в классе >0> сведена к задаче (5), решение которой приведено, например, в [3].
Именно для любого


 ,
,
где
 -
ступенчатая функция, имеющая положительные
скачки в точках
-
ступенчатая функция, имеющая положительные
скачки в точках
 при нечетном n
и в точках
при нечетном n
и в точках
 при четном n,
при четном n,
 -
ступенчатая функция, имеющая положительные
скачки в точках
-
ступенчатая функция, имеющая положительные
скачки в точках
 при нечетном n
и в точках
при нечетном n
и в точках
 при четном n.
при четном n.
Из приведенных выше рассуждений следует, что
 ,
,
 ,
,
где
 ,
,
 ,
,
-
величина скачка функции
 в точке .
в точке .
Литература
Крейн М.Г., Нудельман А.А. Проблема моментов Маркова и экстремальные задачи. – Москва: Наука, 1973.
Таталян К.Р. Экстремальные задачи проблемы моментов на классах распределений. – Дисс. на соиск. ученой степени кандидата физ.-мат. наук. Москва, МИЭМ, 1988.
Карлин С., Стадден В. Чебышевские системы и их применение в анализе и статистике. – Москва: Наука, 1976.
Даниэлян Э.А., Таталян К.Р. О проблеме моментов на мажоризируемых классах. – Ереван: Межвуз. сб. научн. трудов “Прикладная математика”, № 7, 1988.
Манукян В.Р. О проблеме моментов для индексационных классов распределений. – Ереван: ДАН РА, том XCI, № 4, 1990.