Статистические расчеты (работа 1)
Министерство образования и науки Украины
Донбасская государственная машиностроительная академия
Контрольная работа по дисциплине
«Статистика»
2009
Задача №1
Имеются следующие данные о рабочих одного из участников механического цеха:
Таблица 1 – Исходные данные
|
№ рабочего |
Возраст, лет |
Месячная зарплата, грн |
№ рабочего |
Возраст, лет |
Месячная зарплата, грн |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
24 |
180,0 |
11 |
19 |
100,0 |
|
2 |
24 |
220,0 |
12 |
37 |
260,0 |
|
3 |
44 |
390,0 |
13 |
28 |
190,0 |
|
4 |
45 |
310,0 |
14 |
30 |
210,0 |
|
5 |
44 |
260,0 |
15 |
27 |
210,0 |
|
6 |
50 |
300,0 |
16 |
36 |
310,0 |
|
7 |
25 |
240,0 |
17 |
41 |
330,0 |
|
8 |
36 |
250,0 |
18 |
28 |
250,0 |
|
9 |
54 |
390,0 |
19 |
35 |
280,0 |
|
10 |
29 |
250,0 |
20 |
25 |
280,0 |
Для выявления зависимости между возрастом рабочих и оплатой их труда произведите их группировку по возрасту, образовав 5 групп с равными интервалами. По каждой группе и в целом по совокупности рабочих подсчитайте: 1) число рабочих; 2) среднюю заработную плату; 3) средний возраст. Результаты представьте в виде таблицы. Сделайте выводы.
Решение
Для группировки используем следующий алгоритм:
Определим размах вариации
 .
.
Определим величину интервала
 .
.
Таким образом, получаем следующие интервалы: 19-25; 25-32; 32-39; 39-46, 46-54.
Группировка по возрасту показана в таблице 2.
Таблица 2 – Группировка рабочих по возрасту
|
№ подгруппы |
Возрастной интервал, годы |
№ рабочего в списке |
Возраст, лет |
Месячная зарплата, грн |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
19-26 |
1 |
24 |
180,0 |
|
2 |
24 |
220,0 |
||
|
7 |
25 |
240,0 |
||
|
11 |
19 |
100,0 |
||
|
20 |
25 |
280,0 |
||
|
2 |
26-33 |
10 |
29 |
250,0 |
|
14 |
30 |
220,0 |
||
|
15 |
27 |
210,0 |
||
|
18 |
28 |
240,0 |
||
|
3 |
33-40 |
8 |
36 |
290,0 |
|
12 |
37 |
280,0 |
||
|
13 |
28 |
190,0 |
||
|
16 |
36 |
300,0 |
||
|
19 |
35 |
280,0 |
||
|
4 |
40-47 |
3 |
44 |
390,0 |
|
4 |
45 |
320,0 |
||
|
5 |
44 |
260,0 |
||
|
17 |
41 |
330,0 |
||
|
5 |
47-54 |
6 |
50 |
310,0 |
|
9 |
54 |
390,0 |
Таблица 3 – Средняя заработная плата и средний возраст по возрастным группам
|
№ подгруппы |
Возрастной интервал, годы |
Число рабочих, чел. |
Средняя заработная плата, грн. |
Средний возраст, годы. |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
До 26 |
5 |
204,0 |
23,4 |
|
2 |
26-33 |
4 |
230,0 |
28,5 |
|
3 |
33-40 |
5 |
268,0 |
34,4 |
|
4 |
40-47 |
4 |
325,0 |
43,5 |
|
5 |
Свыше 47 |
2 |
350,0 |
52,0 |
Средняя заработная плата по группам определялась суммированием заработной платы отдельных рабочих (графа 4 таблицы 2) и делением суммы на количество рабочих, попавших в данную возрастную подгруппу (графа 3 таблицы 2). Аналогично определялся средний возраст рабочих по подгруппам.
Средняя заработная плата по совокупности определялась суммированием заработной платы отдельных рабочих (графа 5 таблицы 2) и делением суммы на общее количество рабочих n =20. Аналогично определялся средний возраст рабочих по подгруппам.
Вывод.
Таким образом, как видно из таблицы 3, с увеличением возраста рабочих средняя заработная плата повышается.
Задача №2
Имеются следующие данные о размерах затрат на гривну товарной продукции на предприятиях города:
Таблица 4
|
Затраты на гривну товарной продукции |
Число предприятий, шт |
Товарная продукция, млн. грн. |
Середина
|
|
1 |
2 |
3 |
4 |
|
До 85 |
8 |
11 |
82,5 |
|
85-90 |
10 |
22 |
87,5 |
|
90-95 |
5 |
9 |
92,5 |
|
95-100 |
4 |
5 |
97,5 |
|
Итого |
27 |
47 |
Вычислить: 1) средний размер затрат на гривну товарной продукции; 2) средний объем товарной продукции на одно предприятие. Сделать выводы.
Решение
Рассчитывается середина интервала для каждой группы предприятий. для чего определяется интервал, который равен 5. Срединные значения интервалов представлены в табл.4.
Средний размер затрат на гривну товарной продукции определяется по формуле средней арифметической взвешенной.
 ,
,
Где
 - суммарные затраты по всем
группам предприятий;
- суммарные затраты по всем
группам предприятий;
 - количество предприятий.
- количество предприятий.
 .
.
Т.о. средний размер затрат на гривну товарной продукции равен 88,426.
Аналогично определяем средний объем товарной продукции на одно предприятие в млн.грн. В этом случае
 - заданная в условии товарная
продукция по группам предприятий;
- заданная в условии товарная
продукция по группам предприятий;
 - число предприятий, попавших в
данную группу.
- число предприятий, попавших в
данную группу.
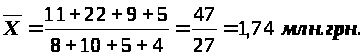
Задача №3
Имеются следующие данные о производстве продукции промышленного предприятия за 2004 – 2009 г.г. (в сопоставимых ценах, млн. грн.):
|
2004 г. |
8,2 |
2007 г. |
9,7 |
|
2005 г. |
8,5 |
2008 г. |
10,5 |
|
2006 г. |
8,6 |
2009 г. |
10,8 |
Исчислить аналитические показатели ряда динамики продукции предприятия за 2004 – 2009 г.г.: абсолютные приросты, темпы роста и темпы прироста, абсолютное значение 1% прироста, а также средние обобщающие показатели ряда динамики.
Решение
Таблица 5 – Основные показатели динамики продукции предприятия
|
Годы |
Производство продукции, млн.грн. |
Абсолютные приросты, млн.грн. |
Темпы роста, % |
Темпы прироста, % |
Абсолютное значение 1% прироста, млн.грн. |
|||
|
С предыдущ. годом |
С 2004г. |
С предыдущ. годом |
С 2004г. |
С предыдущ. годом |
С 2004г. |
|||
|
2004 |
8,2 |
- |
- |
- |
100,00 |
0,00 |
- |
- |
|
2005 |
8,5 |
0,3 |
0,4 |
103,66 |
103,66 |
3,66 |
3,66 |
0,082 |
|
2006 |
8,6 |
0,1 |
0,9 |
101,18 |
104,88 |
1,18 |
4,88 |
0,085 |
|
2007 |
9,7 |
1,1 |
1,5 |
112,79 |
118,29 |
12,79 |
18,29 |
0,086 |
|
2008 |
10,5 |
0,8 |
2,1 |
108,25 |
128,05 |
8,25 |
28,05 |
0,097 |
|
2009 |
10,8 |
0,3 |
2,8 |
102,86 |
131,71 |
2,86 |
31,71 |
0,105 |
|
Итого |
56,3 |
2,6 |
- |
- |
- |
- |
- |
- |
Показатель абсолютного прироста определяется по формуле
 - по сравнению
с предыдущим годом (графа 3);
- по сравнению
с предыдущим годом (графа 3);
 - по сравнению
с предыдущим годом (графа 4),
- по сравнению
с предыдущим годом (графа 4),
где 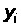 – показатель i-го года;
– показатель i-го года;
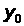 – показатель
базового года
– показатель
базового года
Темпы роста определяются по формуле
 (графа 5) или
(графа 5) или
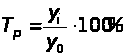 (графа 6).
(графа 6).
Темпы прироста определяются по формуле
 (графа 7) или
(графа 7) или
 (графа 8).
(графа 8).
Показатель абсолютного значения одного процента прироста
 или
или
 (графа 9) .
(графа 9) .
Средний уровень ряда в случае равноотстоящих уровней во времени определяется по формуле средней взвешенной простой

Средний абсолютный прирост
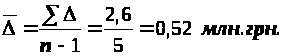
Среднегодовой темп роста
 .
.
Среднегодовой темп прироста

Задача №4
Имеются следующие данные о продаже в городе молока на колхозных рынках и в государственной торговле:
Таблица 6 – Структура продаж молока
|
Место продажи |
Средняя цена за 1 л, коп |
Продано, тыс. л. |
||
|
Базисный период |
Отчетный период |
Базисный период |
Отчетный период |
|
|
В государственной торговле |
80 |
90 |
450 |
840 |
|
На колхозном рынке |
85 |
95 |
320 |
350 |
|
Итого |
770 |
1190 |
Вычислить: 1) индекс цен переменного состава; 2) индекс цен постоянного состава; 3) индекс структурных сдвигов. Покажите зависимость исчисленных индексов. Поясните полученные результаты.
Решение
Индекс цен переменного состава представляет собой отношение средних цен в разных периодах
 ,
,
где  ,
,
 - цены на молоко соответственно в отчетный
и базисный период;
- цены на молоко соответственно в отчетный
и базисный период;
 - объемы
продаж соответственно в отчетный и
базисный период.
- объемы
продаж соответственно в отчетный и
базисный период.
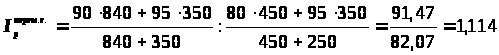
Индекс цен структурного сдвига служит для оценки изменения структуры реализации продукции
 .
.
Индекс цен постоянного состава, не учитывающий изменение структуры:
 .
.
Указанные индексы связаны соотношением
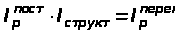 ;
;
1,123·0,993 = 1,114.
Из индекса переменного состава видно, что средняя цена поднялась в отчетном периоде на 11,4% (111,4-100).
Из индекса структуры делаем вывод, что за счет структурных изменений цена снизилась на 0,7% (100-99,3).
Из значения индекса постоянного состава заключаем, что если бы не было структурных изменений в реализации продукции, то цена повысилась бы на 11%.
Задача №5
Имеются следующие данные о норме расхода сырья на единицу изделия:
Таблица 7 – Нормы расхода сырья на единицу изделия
|
Расход сырья, г |
Изготовлено изделий, шт. |
Середина интервала |
|
До 20 |
10 |
19 |
|
20-22 |
13 |
21 |
|
22-24 |
55 |
23 |
|
24-26 |
15 |
25 |
|
Свыше 26 |
7 |
27 |
|
Итого |
100 |
Определить: 1) средний расход сырья на одно изделие; 2) среднее линейное отклонение; 3) дисперсию и среднее квадратическое отклонение; 4) коэффициент вариации. Сделайте выводы.
Решение
1) Средний расход сырья на одно изделие определяется по формуле средней арифметической взвешенной
 ,
,
где 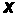 - значение середины интервала для каждого
диапазона расхода сырья;
- значение середины интервала для каждого
диапазона расхода сырья;
 - количество изделий, изготовленных
с указанным расходом сырья.
- количество изделий, изготовленных
с указанным расходом сырья.
 .
.
2) Среднее линейное отклонение определяется по формуле


3) Дисперсия определяется по формуле

 .
.
4) Среднеквадратическое отклонение определяем по формуле
 .
.
5) Коэффициент вариации
 .
.
Т.о., можно сделать вывод об однородности представленной совокупности данных.
Задача №6
Для определения срока службы металлорежущих станков проведено 10%-е выборочное обследование по методу случайного бесповторного отбора, в результате которого получены следующие данные:
Таблица 8
|
Срок службы станков, лет |
Середина интервала, лет |
Число станков, шт. |
|
До 4 |
3 |
15 |
|
4-6 |
5 |
20 |
|
6-8 |
7 |
40 |
|
8-10 |
9 |
20 |
|
Свыше 10 |
11 |
5 |
|
Итого |
100 |
Определить: с вероятностью 0,997 предельную ошибку выборки и пределы, в которых ожидается средний срок службы металлорежущих станков.
Решение
Сначала необходимо найти середины интервалов. Затем на основании имеющегося распределения определим выборочные среднюю и дисперсию.
 ,
,
где 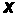 - значение середины интервала для каждого
срока службы;
- значение середины интервала для каждого
срока службы;
 - количество станков, отработавших
указанное количество лет.
- количество станков, отработавших
указанное количество лет.
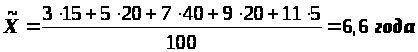
Дисперсия определяется по формуле
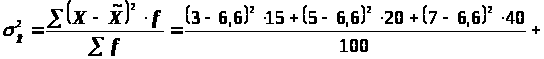
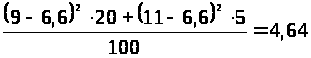 .
.
При р = 0,997 t = 3.
Общий объем выборки
 .
.
Тогда предельная ошибка выборки при бесповторном отборе определяется, как
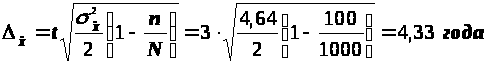 .
.
Следовательно, пределы генеральной средней
 .
.
Т.о., с вероятностью 0,997 можно утверждать лишь то, что средний срок службы станков лежит от 2,3 до 10,9 года.
Задача №7
По данным задачи 1 для выявления тесноты связи между возрастом рабочих и оплатой труда вычислить коэффициент детерминации.
Решение
Опираясь на данные таблиц 2 и 3 сформируем таблицу 9.
Таблица 9 – Средняя заработная плата по возрастным группам
|
№ подгруппы |
Возрастной интервал, годы |
Количество рабочих, получающих заработную плату, чел. |
Итого |
Середина интервала |
||
|
До 200 грн. |
200-300 грн. |
Свыше 300 грн. |
||||
|
1 |
До 25,2 |
2 |
3 |
0 |
5 |
22,5 |
|
2 |
25,2-32,4 |
0 |
4 |
0 |
4 |
29,5 |
|
3 |
32,4-39,6 |
0 |
4 |
1 |
5 |
36,5 |
|
4 |
39,6-46,8 |
0 |
1 |
3 |
4 |
43,5 |
|
5 |
Свыше 46,8 |
0 |
0 |
2 |
2 |
50,5 |
|
Итого |
2 |
12 |
6 |
20 |
Коэффициент детерминации определяется по формуле:
 ,
,
где  - внутригрупповая дисперсия,
- внутригрупповая дисперсия,
 - общая дисперсия.
- общая дисперсия.
Средние значения по группам
 ;
;
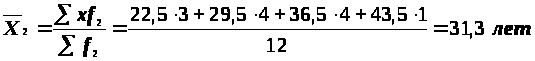 ;
;
 ;
;
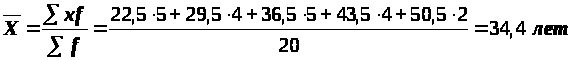 .
.
Внутригрупповая дисперсия
 51.7
51.7
Общая дисперсия
 .
.
 .
.
Коэффициент детерминации
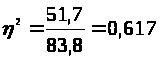 .
.
Эмпирическое корреляционное отношение
 .
.
Т.о. можно говорить о достаточно сильной зависимости возраста работников цеха и их заработной платой.
Список использованных источников
Практикум по теории статистики:Учеб пособие/Под ред. Р.А. Шмойловой. - М:Финансы и статистика, 2001.-416с.
Теория статистики:Учеб пособие/Под ред. Р.А. Шмойловой. - М:Финансы и статистика, 2001.- 560с.