Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца

Министерство образования и науки республики Казахстан

Северо-Казахстанский государственный университет

им. М. Козыбаева

Факультет информационных технологий

Кафедра математики

Курсовая работа

"Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца"

Петропавловск, 2007

Аннотация

В данной курсовой работе исследованы свойства некоторых семейств конечномерных пространств и доказаны интерполяционные теоремы для этих классов пространств.

Содержание

Введение

1. Основные понятия и некоторые классические теоремы теории интерполяции

2. Общие свойства интерполяционных пространств

3. О норме и спектральном радиусе неотрицательных матриц

4. Некоторые интерполяционные свойства семейств конечномерных пространств

Заключение

Список использованной литературы

Введение

Теория интерполяции функциональных пространств как самостоятельная ветвь функционального анализа сформировалась за последние 40-45 лет. Она играет все возрастающую роль в анализе и его приложениях. Центральной темой теории является проблема интерполяции линейных операторов. Эта проблема тесно связана с задачей построения совокупности "промежуточных" пространств – арены, на которой действуют "промежуточные" операторы. Основополагающий вклад в теорию был сделан Эл.-Л. Лионсом, А.П. Кальдероном и С.Г. Крейном. При этом не следует, конечно, забывать, что исследованием названных авторов предшествовали (и стимулировали их) классические теоремы Рисса и Марцинкевича об интерполяции линейных операторов в пространствах l>p>.

Теория интерполяция также применяется в других областях анализа (например, в теории уравнений с частными производными, численном анализе, теории аппроксимации). Рассматривают два существенно различных интерполяционных метода: метод вещественной интерполяции и метод комплексной интерполяции. Модельными примерами для этих методов служат доказательства теоремы Марцинкевича и теоремы Рисса-Торина соответственно. Один из самых ранних примеров интерполяции линейных операторов был предложен Шуром. Шур сформулировал свой результат для билинейных форм, или вернее для матриц, соответствующих этим формам. В 1926 году М. Рисс доказал первую версию теоремы Рисса-Торина с ограничением p≤q, которое как он показал, существенно в случае, когда в качестве скаляров берутся вещественные числа. Основным рабочим инструментом Рисса было неравенство Гельдера. Но в 1938 году Торин привел совершенно новое доказательство и смог устранить ограничение p≤q. В то время как Рисс пользовался вещественными скалярами и неравенством Гельдера, Торин использовал комплексные скаляры и принцип максимума.

1. Основные понятия и некоторые классические теоремы теории интерполяции

Пусть (u,μ) – пространство с мерой μ, которую будем всегда предполагать положительной. Две рассматриваемые функции будем считать равными, если они отличаются друг от друга лишь на множестве нулевой μ-меры. При этом обозначим через l>p>(u,dμ) или просто (l>p>(dμ), l>p>(u) или l>p>) лебегово пространство всех скалярнозначных μ-измерных функций f и u, для которых величина

конечна, здесь 1≤p<∞.

В случае, когда p=∞, пространство l>p> состоит из всех μ-измеримых ограниченных функций. В этом случае

Пусть T - линейное отображение пространства l>p>=l>p>(u,dμ) в пространство l>q>=l>q>(v,dν). Это означает, что T(αf+βg)=αT(f)+βT(g).

Если к тому же T- ограниченное отображение, то есть если величина конечна, то пишут T: lplq.

Число μ называется нормой отображения T. Справедливы следующие известные теоремы:

Теорема 1.1 (интерполяционная теорема Рисса-Торина)

Предположим, что и что T: с нормой μ>0> и T : с нормой μ>1>.

Тогда T: → с нормой μ, удовлетворяющей неравенству 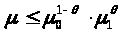(*), при условии, что 0<θ<1 и ; .

Неравенство (*) означает, что μ как функция от θ логарифмически выпукла, то есть lnμ – выпуклая функция.

Доказательство теоремы приведено в [1].

Для скалярнозначной μ-измерной функции f, принимающей почти всюду конечные значения, введем функцию распределения m(σ,f) по формуле

Ясно, что m(σ,f) представляет собой вещественнозначную функцию от σ, определенную на положительной вещественной полуоси . Очевидно, что m(σ,f) – невозрастающая и непрерывная справа функция. Кроме того,

при 1≤p<∞

и .

Используя функцию распределения m(σ,f), введем теперь слабые l>p>-пространства, обозначаемые через . Пространства , 1≤p<∞, состоит из всех функций f , таких что

В предельном случае p=∞, положим .

Заметим, что не является нормой при 1≤p<∞.

Действительно, ясно, что

Применяя неравенство , заключаем, что

Последнее означает, что представляет собой так называемое квазинормированное векторное пространство. (В отличие от нормированных пространств, где выполняются неравенство треугольника , в квазинормированных пространствах имеет место лишь "квази-неравенство треугольника" для некоторого k≥1.) Однако, при p>1 в пространстве можно ввести норму, при наделении которой оно становится банаховым пространством.

Теорема 1.2 (Интерполяционная теорема Марцинкевича)

Пусть p>0>≠p>1> и

T: с нормой ,

T: с нормой .

Положим ; , и допустим, что p≤q.

Тогда T: →, с нормой μ, удовлетворяющей неравенству .

Эта теорема, напоминает теорему Рисса-Торина, но отличается от нее во многих важных отношениях.

Во-первых, здесь скаляры могут быть как вещественными, так и комплексными, в то время как в теореме Рисса-Торина обязательно нужно, чтобы скаляры были комплексными. Во-вторых здесь имеется ограничение p≤q. Наиболее важная особенность состоит в том, что в предпосылках теоремы пространства и заменены на более широкие пространства и .

Таким образом, теорема Марцинкевича может оказаться применимой в тех случаях, где теорема Рисса-Торина уже не работает.

2. Общие свойства интерполяционных пространств

Пусть A - векторное пространство над полем вещественных или комплексных чисел. Оно называется нормированным векторных пространством, если существует вещественнозначная функция (норма) , определенная на A, удовлетворяющая условием.

1) , причем

2) (λ-скаляр)

3) .

Пусть A и B – два нормированных векторных пространства. Отображение T из A в B называется ограниченным линейным оператором, если

, и .

Ясно, что всякий ограниченный линейный оператор непрерывен.

Пусть A>0> и A>1> – топологических векторных пространства. Говорят, что

A>0> и A>1 >совместимы, если существует отделимое топологическое векторное пространство U, такое, что A>0> и A>1>, являются подпространствами. В этом случае можно образовать сумму A>0> + A>1>, и пересечение A>0>∩A>1>. Сумма состоит из всех aU, представимых в виде a=a>0>+a>1>, где a>0>A, и a>1>A,

Справедлива следующая лемма

Лемма 2.1. Пусть A>0> и A>1>-совместимые нормированные векторные пространства. Тогда

A>0>∩A>1>, есть нормированное векторное пространство с нормой

>>

A>0> + A>1>, также представляет собой нормированное векторное пространство с нормой

>>

При этом если A>0> и A>1> – полные пространства, то A>0>∩A>1> и A>0> + A>1> также полны.

Дадим некоторые важные определения:

Категория σ состоит из объектов A,B,C…., и морфизмов R,S,T,…. между объектами и морфизмами определено трехместное отношение T: A↷B.

Если T: A↷B и S: B↷C, то существует морфизм ST, называемый произведением (или композицией) морфизмов S и T, такой, что ST: A↷ C.

Операция взятия произведения морфизмов удовлетворяет закону ассоциативности: T(SR)=(TS)R. далее, для всякого объекта A из σ существует морфизм I=I>A>, такой, что для любого морфизма T: A↷A TI=IT=T

Через σ>1> обозначим категорию всех совместимых пар пространств из σ.

Определение 2.1. Пусть =(A>0>,A>1>)-заданная пара из σ>1>. Пространство A из σ будем называть промежуточным между A>0> и A>1> (или относительно ), если имеют место непрерывные вложения.

.

Если, кроме, того T: ↷ влечет T: A ↷ A, то A называется интерполяционным пространством между A>0> и A>1>.

Более общим образом, пусть и - две пары из σ>1>. Тогда два пространства A и B из σ называются интерполяционными относительно и соответственно и T: ↷ влечет T: A↷ B.

Если выполнено

,

В этом случае, говорят, что A и B равномерные интерполяционные пространства.

Определение 2.2 Интерполяционные пространства A и B называются пространствами типа θ (0≤θ≤1), если

В случае с=1 говорят, что A и B - точные интерполяционные пространства типа θ.

3. О норме и спектральном радиусе неотрицательных матриц

Хорошо известно, что проблема нахождения нормы линейного оператора, спектрального радиуса оператора являются трудной проблемой и в конечномерном случае. В то же время, иногда важно не вычисляя нормы оператора знать, как она изменится в случае некоторого преобразования.

В данной работе изучается влияние распределения ненулевых элементов неотрицательной матрицы на норму соответствующего оператора и спектрального радиуса.

Определим пространство как множество всех наборов вида

a=(a>1>, a>2>,…, a>N>)

с нормой

.

Множество Q={(k,l):k,l=1,…,N} назовем решеткой размерности N x N. Любое множество Q>0>={(k>i>,l>j>): , } будет являться подрешеткой размерности r x m.

Спектральный радиус линейного оператора в конечномерном пространстве определяется следующим образом:

r(A)=,

где >k>- собственные значения оператора A.

Пусть m ≤ N, d>1>,…,d>m> - положительные числа. Через D>m> обозначим множество неотрицательных матриц А, ненулевые элементы которых принимают значения d>1>,…,d>m>. Через P(A) обозначим множество индексов соответствующих положительным элементам. Пусть AD>m>. Если D={(k>i>,l>j>), i=1,…,q, j=1,…,p} подрешетка, содержащая P(A), то для соответствующего оператора А

Как видно из этого определения, от перестановки строк и столбцов матрицы норма не меняется.

Пусть даны положительные числа d>1>,…,d>m> и натуральное число m < N2.

Будем исследовать следующие вопросы:

Как расположить числа d>1>,…,d>m> в решетке Q, чтобы норма линейного оператора A>Q> соответствующего решетке (матрице) Q была максимальной?

Пусть в неотрицательной решетке Q m положительных элементов. Как расположить (m+1)-ый элемент, чтобы норма линейного оператора A>Q>> >соответствующей полученной решетке была максимальной?

Как расположить числа d>1>,…,d>m> в решетке Q, чтобы спектральный радиус был минимальным (максимальным)?

Справедливы следующие теоремы:

Теорема 3.1 Пусть d>1>,…,d>m> положительные числа, D>m>> >- класс неотрицательных матриц, ненулевые элементы которых принимают значения d>1>,…,d>m>. Если m ≤ N, Q>0 >-произвольная подрешетка размерности 1 m, то

.

Доказательство. Воспользуемся определением и неравенством Коши-Буняковского, получаем

Неравенство в обратную сторону очевидно.

Теорема доказана.

Данное утверждение говорит о том, что если ненулевых элементов меньше либо равно N, то своего максимума норма достигается когда все ненулевые элементы расположены в одной строке или в одном столбце.

Теорема 3.2 Пусть d>1>=…=d>m>=d, то есть D>m>> >– множество всех матриц, имеющие m ненулевых элементов, которые равны числу d. Q>0 >-произвольная решетка, симметричная относительно главной диагонали размерности nn, где n=min{r: r2 ≥ m}. Тогда

,

где [m1/2] - целая часть числа m1/2.

Доказательство. Из свойства спектрального радиуса имеем для AD>m>

.

Пусть Q>1 >-подрешетка, также симметричная относительно главной диагонали размерности . Тогда для AD>m>, Q>1>P(A)Q>0> имеет место представление

А=А>1>+А>0>, где А>1>,А>0>D>m>, Р(А>1>)=Q>1>, P(A>0>)Q>1>\Q>0>.

Учитывая, что матрицы А>0> и А>1> неотрицательны, получаем

,

поэтому r(A>0>)≤r(A).

С другой стороны А>1> – симметричная матрица и следовательно

.

Таким образом,

.

Теорема доказана.

Теорема 3.3 Пусть множество GQ, где Q - решетка размерности nn таково, что, если (k,l)G, то (l,m),(n,k)G для всех n,m{1,2,…,N}.

Тогда, если P(A)G, то r(P(A))=0.

Доказательство. Не трудно проверить, что для матрицы А с ненулевыми элементами из G (т.е. P(A)G) имеет место равенство А2=0, т.е. А – нильпотентная матрица индекса 2 и следовательно у нее единственное собственное значение 0.

Теорема доказана.

Теорема 3.4 Пусть AD>m>. Пусть Q>0> -минимальная подрешетка содержащая P(A), (Q>0>P(A)) такая, что в каждой строке и в каждом столбце находится хотя бы один элемент соответствующий нулевому элементу матрицы A.

Пусть A>d> – матрица, полученная из матрицы A добавлением элемента со значением d>0 в одно из свободных мест, тогда

Доказательство.

Так как норма оператора не зависит от перестановки строк и столбцов матрицы, то можно считать, что решетка A>0>={(i,j), i=1,…,l; j=1,…,m} расположена в левом верхнем углу матрицы A. Пусть добавлен еще один ненулевой элемент d с координатами (i>0>,j>0>) вне решетки Q>0>. Возможны три случая:

    1 ≤ i>0 >≤ l, j>0 >> m;

    i>0 >> l, 1 ≤ j>0 >≤ m;

    i>0 >> l, j>0 >> m.

Рассмотрим первый случай. Не уменьшая общности положим, что этот ненулевой элемент соответствует индексу (1, m+1). По условию теоремы в каждой строке и в каждом столбце имеется хотя бы один нулевой элемент и мы можем предположить, что a>1>>m>=0. Получаем:

Используя неравенства

,

имеем:

Пусть z>1>=x>1>, z>2>=x>2>,…,z>m>= и

,

тогда

где элемент 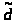имеет координаты (1,m).

Следовательно

Рассмотрим второй случай. Пусть добавленный ненулевой элемент соответствует индексу (l+1,1). Учитывая, что в каждой строке и в каждом столбце решетки есть хотя бы один ненулевой элемент и то, что от перестановки строк норма матрицы не меняется, мы можем предположить, что a>l>>1>=0. Аналогично первому случаю имеем:

.

Используя неравенства

,

получаем:

.

Пусть z>1>=y>1>, z>2>=y>2>,…,z>m>= и

,

тогда

где элемент 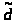имеет координаты (l,1). Следовательно

Рассмотрим последний случай. Не уменьшая общности положим, что этот ненулевой элемент соответствует индексу (l+1, m+1). В этом случае нужно учесть, что от перестановки строк и столбцов норма матрицы не изменится, поэтому можно положить, что a>lm>=0. Рассуждая также, как и в предыдущих случаях, получаем:

где элемент 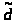имеет координаты (l,m).

Теорема доказана. Аналогичные задачи для интегральных операторов были рассмотрены в работах [1], [5].

4. Некоторые интерполяционные свойства семейств конечномерных пространств

Пусть 1 ≤ p < ∞, 1 ≤ q ≤ ∞. Определим семейство конечномерных пространств:

где невозрастающая перестановка последовательности . Обозначим через –множество всех непустых подмножеств из {1,2,...N} Пусть M , 1 ≤ p < ∞, 1 ≤ q ≤ ∞, множество M назовем сетью.

Определим семейство конечномерных пространств

|e| - количество элементов множества e.

При q=∞ положим

Данные пространства являются конечномерными аналогами сетевых пространств, введенных в [1].

Будем говорить что {AN} ↪ {BN} если существует константа c, такая что для любого , где c не зависит от .

Лемма 4.1 Пусть 1 ≤ q <q>1>≤ ∞, 1 ≤ p ≤ ∞, . Тогда имеет место вложение

↪

то есть

где с не зависит от выбора N.

Доказательство. Пусть

(1)

то есть ↪

Теперь рассмотрим случай, когда 1 ≤ q <q>1>< ∞, и воспользуемся неравенством (1)

Лемма доказана.

Лемма 4.2 Пусть 1≤p<p>1><∞, 1≤q,q>1>≤∞. Тогда имеем место вложение

↪

Доказательство.

Согласно условию леммы, нам достаточно доказать вложения при p < p>1 :>

↪

Получаем:

Лемма доказана.

Лемма 4.3 Пусть 1<p<∞, 1≤q≤∞, M= . Тогда

Равенства понимаются с точностью до эквивалентности норм, причем константы не зависят от.

Доказательство. Сначала докажем соотношение:

(2)

Заметим, что

Поэтому

Теперь покажем обратное неравенство. Пусть . Учитывая выбор имеем.

~

~

Заметим, что

Согласно (2) получаем:

то есть ↪.

Докажем обратное включение. Пусть Введем следующие обозначения:

Тогда

.

Пусть для определенности

.

Возможны следующие случаи:

.

В первом случае получаем, что

.

Во втором случае , следовательно . Представим , тогда . Здесь и далее - целая часть числа .

Получаем

Заметим, что существует такое, что

Положим Тогда .

.

Таким образом, получаем

Из того, что

Имеем

То есть . Следовательно ↪ где соответствующие константы не зависят от N.

Лемма доказана.

Для пары пространств определим интерполяционные пространства аналогично [5] .

Пусть , тогда

где

При q=∞

Лемма 4.4 Пусть , d>1. Тогда

Справедлива следующая

Теорема 4.1 Пусть ≤p>0><p>1><∞, 1<q>0>,q>1>≤∞, M – произвольная сеть. Тогда

↪

где

Доказательство.

Учитывая, что ↪нам достаточно, доказать следующее вложение

↪

Пусть Рассмотрим произвольное представление a=a>0>+a>1>, где

тогда

(3)

Так как представление a=a>0>+a>1> произвольно, то из (3) следует

Где Рассматривая норму элемента в пространстве и применяя

лемму 4.4 , получаем:

Теорема доказана.

Теорема 4.2 Пусть 1≤p>0><p>1><∞, 1<q>0>,q>1>≤∞, Тогда имеет место равенство

Это равенство понимается в смысле эквивалентности норм с константами, не зависящими N.

Доказательство. По теореме 4.1 и того, что является обобщением пространств Лоренца нам достаточно доказать следующее вложение:

↩

.

Определим элементы и следующим образом

, тогда .

Заметим что

(4)

где

(5)

где

Тогда

Из (4) и (5) имеем:

Оценим отдельно каждое из слагаемых последнего равенства, используя неравенство Гельдера:

~

где .

Таким образом, получаем, что Аналогично рассмотрим второе слагаемое:

~

~

~

Таким образом, получаем

где c не зависит от .

Теорема доказана.

Теорема 4.3 Пусть - матрица , тогда

~

Причем соответствующие константы не зависят от

Доказательство.

Воспользуемся эквивалентными представлением нормы и неравенством о перестановках, получим

~

где - невозрастающая перестановка последовательности

Применим неравенство Гельдера

Учитывая лемму 3, имеем

Обратно, пусть e произвольное множество из M>1>, , где

Тогда

В силу произвольности выбора e из M>1> получаем требуемый результат.

Следствие. Пусть - матрица

p>0><p>1>, q>0><q>1>, тогда

Доказательство. Из теоремы 3 следует, что

Воспользуемся интерполяционными теоремами 1,2, получаем

то есть

С другой стороны по лемме 1 и теореме 3 имеем

,

Следствие доказано.

Заключение

В данной курсовой работе приведены и доказаны некоторые свойства конечномерных пространств, а именно пространств Лоренца и сетевых пространств.

Полученные результаты могут быть полезны для студентов, магистрантов, аспирантов и преподавателей. Кроме того, данный материал может быть использован для чтения спецкурсов и спецсеминаров.

Список использованной литературы

    Берг Й., Лефстрем Й. Интерполяционные пространства. Введение. М.: Мир, 1980.

    Гохберг И.Ц., Крейн М.Г. Введение в теорию линейных несамосопряженных операторов. М.: Наука, 1965.

    Костюченко А.Г., Нурсултанов Е.Д. Об интегральных операторах в пространствах. Фундаментальная и прикладная математика. Т.5. №2, 1999. С. 475-491.

    Костюченко А.Г., Нурсултанов Е.Д. Теория управления катастрофами. //Успехи математических наук, 1998. Т.53. Выпуск 2.

    Нурсултанов Е.Д. Сетевые пространства и неравенства типа Харди-Литтлвуда //Матем.сборник.-1998.-Т.189, №3.-С.83-102.

    Таджигитов А.А. О зависимости нормы матрицы от взаимного расположения ее элементов. // Материалы Международной научной конференции "Современные проблемы теории функций и их приложения", Саратов, Россия, 2004, с. 177-178.

    Таджигитов А.А. О норме и спектральном радиусе неотрицательных матриц. //Материалы Международной научно-практической конференции "Современные исследования в астрофизике и физико-математических науках", Петропавловск, 2004, с. 104-107.

    Таджигитов А.А. Интерполяционные свойства конечномерных пространств. //Международная научная конференция студентов, аспирантов и молодых ученых "Ломоносов 2005", Астана, 2005, с. 41-42.