Дифференциальные уравнения (работа 4)
Министерство образования РФ
Московский авиационный институт
(государственный технический университет)
Филиал "Восход"
Кафедра МиПОИС
Курсовая работа
по курсу: Дифференциальные уравнения
Студент гр. ДА 2-40
Воронцов О. В.
Байконур 2005 г.
1. Теоретическая часть
Дифференциальные уравнения, приводящиеся к однородным
Дифференциальные уравнения, которые приводятся к однородным, имеют вид:
Возможны три случая:
Когда C>1>=C>2 >=0
Когда
Когда
Вводятся новые переменные u и υ так, чтобы правая часть исходного уравнения в этих переменных была однородной функцией нулевого порядка. А именно, делается замена x=u+h, y= υ+k и подбираются постоянные h и k таким образом, чтобы в правой части исходного уравнения после подстановки пропали свободные члены. При подстановке x=u+h, y= υ+k в дробь приравниваются нулю свободные члены числителя и знаменателя, то есть записываются два равенства:
Определитель данной системы
линейных алгебраических уравнений:
,
не равен нулю по условию, поэтому система
имеет единственное решение, то есть
существует единственная пара чисел h
и k,
такая что при подстановке x=u+h,
y=
υ+k
правая часть исходного уравнения
принимает вид
,
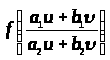а само уравнение:
.
Полученное уравнение является однородным
2. Практическая часть
Задача 1. Найти общий интеграл дифференциального уравнения:
Решение:
– дифференциальное уравнение с разделяющимися переменными
Разделим переменные:
Проинтегрируем выражение:
Ответ:
Задача 2. Найти общий интеграл дифференциального уравнения:
Решение:
Следовательно, исходное уравнение является однородным.
Пусть
Произведём замену в исходном уравнении:
- дифференциальное уравнение с
разделяющимися переменными
Разделим переменные:
Проинтегрируем а затем пропотенцируем выражение:
Но
Ответ:
Задача 3. Найти общий интеграл:
Решение:
- дифференциальное уравнение,
приводящееся к однородному
Введём новые элементы:
,
где h и k должны удовлетворять уравнениям:
откуда
Таким образом:
откуда
Подставляя это в исходное уравнение, получим
Или
Сделаем подстановку:
-
дифференциальное уравнение с разделяющимися переменными
Упростим левую часть выражения
1+z=A(z-1)+Bz
Z1: 1=A+B A=-1
z0: 1=-A B=2
Проинтегрируем уравнение (**)
ln|z|–2ln|z–1|=ln|U|+C
Пропотенцируем и подставим значение z в выражение
Упрощая данное выражение, получим:
Ответ:
Задача 4. Найти решение задачи
Коши:
Решение:
–
линейное уравнение
Воспользуемся методом Бернулли:
a)
Разделим переменные:
Проинтегрируем а затем пропотенцируем данное выражение:
б)
Разделяя переменные, подставляя значение υ и интегрируя выражение получим:
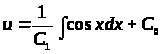
Следовательно:
Найдём значение С>2>
y|>п>>/4>=1/2
Ответ:
Задача 5. Решить задачу Коши:
Решение:
- линейное уравнение
Воспользуемся методом интегрирующего множителя:
Ответ:
Задача 6. Найти решение задачи
Коши:
,
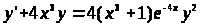y(0)=1
Решение:
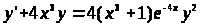- уравнение Бернулли
Подёлим данное уравнение на (:y2):
Произведём замену и подставим её в исходное уравнение:
z=y-1
Следовательно:
- линейное уравнение
Воспользуемся методом Бернулли:
Откуда:
Найдём значение С>2>
Следовательно:
Ответ:
Задача 7. Найти общий интеграл дифференциального уравнения:
Решение:
- дифференциальное уравнение в полных дифференциалах
Следовательно, левая часть
уравнения является полным дифференциалом
некоторой функции
(*)
Интегрируем по x первое из уравнений (*), при этом считаем, что С является функцией от y:
Дифференцируя полученное, имеем:
Но
Откуда:
Следовательно:
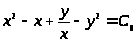
Ответ:
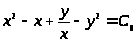
Задача 8. Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку М.
Решение:
Чтобы решить данное дифференциальное уравнение необходимо построить семейство изоклин, показать на них угол наклона касательных и построить интегральные кривые таким образом, чтобы они пересекали изоклины под соответствующим углом:
Откуда
В результате получим следующий график:
Задача 9. Найти линию, проходящую
через точку М>0>
и обладающую тем свойством, что в любой
точке М нормальный вектор
с концом на оси ординат имеет длину
равную а и образует угол с положительным
направлением оси ординат. М>0>(6;4),
a=10
Решение:
Подставляя значения функции в точке M найдём значение С:
Ответ:
Задача 10. Найти общее решение дифференциального уравнения:
Решение:
- дифференциальное уравнение
третьего порядка
Пусть
Подставив в исходное уравнение, получим:
Проинтегрируем и поделим на х данное выражение:
Следовательно:
Разделяя переменные и вновь интегрируя, получим:
Повторяем процедуру в третий раз и получаем искомое выражение для y
Ответ:
Задача 11. Найти общее решение дифференциального уравнения:
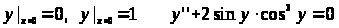
Решение:
Данное уравнение не содержит х в явном виде
Предположим, что
откуда
Тогда исходное уравнение будет выглядеть так:
Разделим переменные и проинтегрируем выражение:
Но.
Тогда
Однако:
.
Поэтому разделим переменные и
проинтегрируем выражение:
Выясним значение С>2>:
Следовательно:
Ответ:
Задача 12. Найти общее решение дифференциального уравнения:
Решение:
- НЛДУ четвёртого порядка
Решение будет записано в виде:
Запишем однородное линейное дифференциальное уравнение (ОЛДУ):
Составим и решим для ОЛДУ характеристическое уравнение:
k4-3k3+3k2-k=0
k>1>=0
k3-3k2+3k-1=0
k>2>=1
по методу Горнера:
1 -3 3 -1
1 1 -2 1 0
k3-2k2+1=0
k>3,4>=1
Общее решение будет равно:
Найдём частное решение:
6A-2Ax-B=2x
Откуда:
Ответ:
Задача 13. Найти общее решение дифференциального уравнения:
Решение:
- НЛДУ с постоянными коэффициентами
Составим ОЛДУ и решим соответствующее характеристическое уравнение
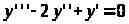
Решение НЛДУ запишется в виде:
Общее решение:
Найдём частное решение дифференциального уравнения:
Подставим найдённое в исходное уравнение и выразим коэффициенты
=>
Частное решение:
Решение дифференциального уравнения:
Ответ:
Задача 14. Найти общее решение дифференциального уравнения
Решение:
- НЛДУ с постоянными коэффициентами
Общее решение
Найдём частное решение:
Подставим найдённое в исходное уравнение и выразим неизвестные коэффициенты:
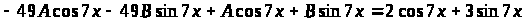
Частное решение уравнения:
=
Ответ:
=
Задача 15. Найти общее решение
дифференциального уравнения:
Решение:
По определению гиперболического синуса:
Найдём общее решение
Найдём частное решение:
Подставив в исходные уравнения, найдём значения коэффициентов:
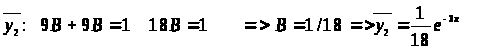
Ответ:
Задача 16. Решить задачу Коши:
,
,
Решение:
- НЛДУ
Общее решение запишем в виде
Запишем ОЛДУ и найдём корни его характеристического уравнения:
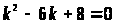
Общее решение имеет вид:
Найдём решение частное:
,
где С>1> и С>2>– решения системы дифференциальных уравнений
По теореме Крамера:
Интегрируя выражения, получим:
Следовательно, решение будет выглядеть так:
Найдём значения С>1> и С>2>
Ответ:
Задача 17. Решить систему дифференциальных уравнений
Решение:
Составим матрицу системы:
Составим характеристическое уравнение det(A-λE)=0, то есть:
Найдём собственные векторы
1)
2)
Запишем общее решение системы уравнений
Отсюда получаем:
Ответ:
Задача 18. Найти кривые, у которых точка пересечения любых касательных с осью абсцисс имеет абсциссу, вдвое меньшую абсциссы точки касания.
Решение:
Но
=>
Разделим переменные:
Проинтегрируем и пропотенцируем выражение:
Ответ: