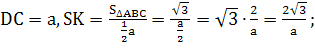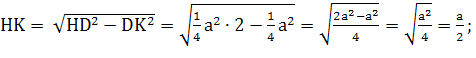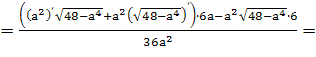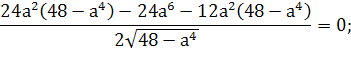Элементы алгебры и геометрии
Контрольная работа
«Элементы алгебры и геометрии»
Вариант 9
Задание № 19
Решить систему трех уравнений с тремя неизвестными при помощи определителей.
Найдем определитель матрицы А:
Δ(А) =
=
= 2 ∙ 1 ∙6 + (-3) (-2) ∙3 + 1 ∙ 1 ∙ (-2) – 1 ∙ 1 ∙ 3 – (-3) ∙ 1 ∙ 6 – 2 (-2) ∙ (-2) =
= 12 + 18 – 2 – 3 + 18 – 8 = 48 – 13 = 35
Δ(А) = 35
Найдём Δ>1>, Δ>2>, Δ>3 >
Δ>1 >=
=
= 3 ∙ 1 ∙ 6 + (-3) (-2) ∙ 0 + 1 ∙ 4 ∙(-2) – 0 ∙1 ∙ 1 – 4 ∙ (-3) ∙ 6 – 3 (-2) (-2) =
= 18 + 0 – 8 – 0 + 72 – 12 = 90 – 20 = 70
Δ>2 >(А) =
=
= 2 ∙ 4 ∙ 6 + 3 ∙ (-2) ∙ 3 + 1 ∙ 1 ∙ 0 – 3 ∙ 4 ∙ 1 – 1 ∙ 3 ∙ 6 – 2 ∙ 0 ∙ (-2) =
= 48 – 18 + 0 – 12 -18 – 0 = 0
Δ>3 >=
=
= 2 ∙ 1 ∙ 0 + (-3) 4 ∙ 3 + 3 ∙ 1 ∙(-2) – 3 ∙1 ∙ 3 – 1 ∙ (-3) ∙ 0 – 2 ∙ (-2) 4 =
= 0 – 36 – 6 – 9 + 0 + 16 = – 20 – 15 = – 35
Найдем корни:
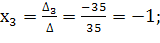
Ответ: 2; 0; –1
Задание № 40
Исследовать данную систему уравнений на совместность и решить её, если она совместна.
Запишем матрицу А и найдем ранг матрицы А:
Поменяем местами первую и вторую строки:
Первую строку умножим на 3 и вычтем из неё вторую, первую умножим на 5 и вычтем из неё третью:
Вычтем из второй строки – третью:
Ранг матрицы
Запишем расширенную матрицу
Найдем определитель расширенной матрицы. Поменяем местами первую и вторую строки:
Умножим первую строку на 3 и вычтем из неё вторую, умножим первую строку на 5 и вычтем из неё третью:
Вычтем из второй строки третью:
Ранг расширенной матрицы
Ранг расширенной матрицы системы не равен рангу матрицы системы, значит система несовместна (не имеет решений).
Задание № 54
Даны координаты точек А (х>1>;у>1>) и В (х>2>;у>2>) и радиус окружности R, центр которой находится в начале координат.
Требуется:
1) составить каноническое уравнение эллипса, проходящего через данные точки А и В;
2) найти полуоси, фокусы и эксцентриситет этого эллипса;
3) найти все точки пересечения эллипса с данной окружностью;
4) построить эллипс и окружность.
Решение:
Общий вид канонического уравнения эллипса:
Подставим координаты точек А и В в общее уравнение:
Подставляем найденные переменные в общее уравнение эллипса:
Полуоси:
Точки пересечения данного эллипса с окружностью R=8, найдем решив систему уравнений:
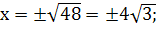
Получили четыре точки пересечения эллипса с окружностью:
4.
Задание № 69
Дано: вершины пирамиды АВСD
Записать векторы
в системе орт и найти их модули:
А (3; 3; –3); В (7; 7; –5); С (5; 14; –13); D (3; 5; –2).
= (7 – 3; 7 – 3; –5 + 3) = (4; 4; –2)$
;
=
= 6;
= (5 – 3; 14 – 3; –13 + 3) = (2; 11; –10);
= 2i + 11j – 10k;
= 15;
= (3 – 3; 5 – 3; –2 + 3) = (0; 2; 1);
=
=
Найти
угол между векторами
и
:
Найти
проекцию вектора
на вектор
:
Найти площадь грани АВС:
=
;
Найти объем пирамиды ABCD:
=
=
Задание № 93
Даны координаты точек А, В, С, М:
А (5; 4; 1); В (–1; –2; –2); С (3; –2; 2); М (–5; 5; 4).
1.Найти уравнение плоскости Q, проходящей через точки А, В, С:
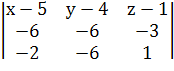= 0;
= 0;
(x – 5)( – 6 – 18) – (y – 4)( – 6 – 6) + (z – 1)(36 – 12) = 0;
– 24(x – 5) + 12(y – 4) + 24(z – 1) = 0;
– 2(x – 5) + (y – 4) + 2(z – 1) = 0;
–2x + 10 + y – 4 + 2z – 2 = 0;
–2x + y + 2z + 4 = 0 – уравнение плоскости Q.
2.Составить каноническое уравнение прямой, проходящей через точку М перпендикулярно плоскости Q:
Подставим координаты точки М (–5; 5; 4) и коэффициенты общего уравнения плоскости Q (–2; 1; 2) в каноническое уравнение прямой:
3.Найти точки пересечения полученной прямой с плоскостью Q и с координатными плоскостями хОу, уОz, xOz: пусть
Где t – некоторый параметр, тогда уравнения прямой можно записать так:
Подставим данные выражения в уравнение плоскости Q и найдем параметр t:
Подставим значение параметра t в уравнения и найдем координаты точки пересечения:
Итак, координаты точки P,
точки пересечения полученной во втором
пункте прямой и плоскости Q:
Р
.
Р>1> – точка пересечения прямой с с хОу: z = 0;
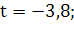
P>1> (2,6; 1,2; 0).
P>2> – точка пересечения прямой с уОz: x = 0;
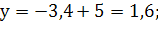
P>2> (0; 1,6;
2,8).
Р>3> - точка пересечения прямой с xOz: y = 0;
;
P>3> (0,5; 0;
1,5).
Найти расстояние от точки М до плоскости Q:
т.к. прямая МР перпендикулярна плоскости Q, точка Р принадлежит плоскости Q, то расстояние между точками М и Р и будет расстоянием от точки М до плоскости Q.
Производная и дифференциал
Задание № 114
Найти пределы:
Разложим на множители и числитель и знаменатель:
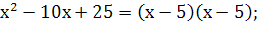
Задание № 135
Функция у задана различными аналитическими выражениями для различных областей изменения аргумента х.
Найти точки разрыва функции, если они существуют.
Данная функция определена и непрерывна
в интервалах (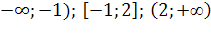
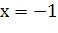При
и
меняется аналитическое выражение
функции и только в этих точках функция
может иметь разрывы.
Определим односторонние пределы в
Т.к. односторонние пределы в
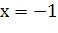не совпадают, значит разрыв I рода.
Определим односторонние пределы в
точке:
Т.к. односторонние пределы в точке
совпадают, значит функция в точке
непрерывна.
2. Найти скачок функции в точке разрыва:
точка
разрыва
Задание № 198
Найти приближенное значение указанных величин с помощью дифференциалов соответствующих функций.
или
Задание № 156
Найти производные
пользуясь формулами дифференцирования:
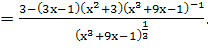
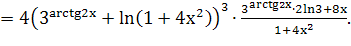
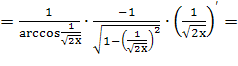
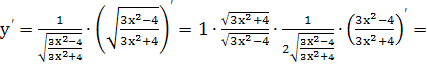
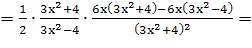
Задание №240
Исследовать функцию методами дифференциального исчисления.
Начертить график.
План исследования:
1.найти область существования функции;
2.исследовать на непрерывность, найти точки разрыва и её односторонние пределы в этих точках;
3. исследовать на четность, нечетность;
4. найти точки экстремума, интервалы возрастания, убывания функции;
5. найти точки перегиба, интервалы выпуклости и вогнутости;
6.асимптоты, если они есть;
7. построить график.
Задание № 272
Требуется поставить палатку в форме
правильной четырехугольной пирамиды
с заданной боковой поверхностью
.
Каковы должны быть размеры палатки
(сторона а и высота h) чтобы
вместимость палатки была наибольшей.
Решение:
Вместимость палатки – это объем палатки.
Объем правильной пирамиды находится
по формуле
где а – сторона квадрата (основание
пирамиды), h – высота
пирамиды.
Выразим высоту пирамиды через сторону квадрата:
