Числа "е" та "пі"

КУРСОВА РОБОТА

з дисципліни

„Вища математика”

за темою

Числа «е» та «пі»

ЗМІСТ

ВСТУП

РОЗДІЛ І ОСОБЛИВІ ЧИСЛА МАТЕМАТИКИ „π.” ТА „е”

1.1 Сутність та історична поява чисел „π.” та „е”

1.2 Визначення понять ірраціональності та трансцендентності чисел

1.3 Доведення ірраціональності та трансцендентності числа „π”

1.4 Доведення ірраціональності та трансцендентності числа „е”

РОЗДІЛ ІІ НАБЛИЖЕНЕ ОБЧИСЛЕННЯ ЧИСЛА „π”

2.1 Методи наближеного обчислення числа „π” за допомогою числових рядів

2.2 Методи наближеного обчислення числа „π” за допомогою розкладу в нескінченні ланцюгові дроби

РОЗДІЛ ІІІ НАБЛИЖЕНЕ ОБЧИСЛЕННЯ ЧИСЛА „е”

3.1 Методи наближеного обчислення числа „е” за допомогою числових рядів

3.2 Методи наближеного обчислення числа „е” за допомогою розкладу в нескінченні ланцюгові дроби

ВИСНОВКИ

СПИСОК ВИСКОРИСТАНОЇ ЛІТЕРАТУРИ

ВСТУП

Сучасна математика в багатьох задачах оперує підмножиною дійсних чисел, що складається з підмножин раціональних і ірраціональних чисел, тобто з чисел які можна представити у вигляді кінцевого алгебраїчного дробу й чисел, та які не можна представити у вигляді кінцевого алгебраїчного дробу. Особливою підмножиною ірраціональних чисел є трансцендентні числа такі числа, які не є коренем ніякого багаточлена із цілими коефіцієнтами.

Існування і явні побудови дійсних трансцендентних чисел обґрунтував французький учений Ж.Ліувілль на основі заміченого їм факту: ірраціональні алгебраїчні числа не допускають «дуже сильних» наближень раціональними числами. Французький учений Е.Борель встановив, що «майже всі» ірраціональні числа трансцендентні.

Усім, хто вперше стикнувся з математикою в школі, відомо про 2 особливих числа:

π – число, рівне відношенню довжини окружності до її діаметра;

та е – основу натуральних логарифмів.

Зазначені числа входять у множину формул математики, фізики, хімії, біології, а також економіки. Це свідчить про те, що вони відбивають деякі самі загальні закони природи.

Хоча ще з кінця 16 в., тобто з тих пор, як сформувалися самі поняття раціональних і ірраціональних чисел, багато вчених були переконані в тім, що  число ірраціональне, але тільки в 1766 німецький математик Іоганн Генріх Ламберт (17281777), ґрунтуючись на відкритій Ойлером залежності між експонентною й тригонометричною функціями, строго довів це – „Число  не може бути представлене у вигляді простого дробу, як не були б великі чисельник і знаменник”.

Також, хоча ще в середині 18 століття виникла гіпотеза про трансцендентність чисел і інших, доказ цього довго не вдавалося одержати. Трансцендентність числа е довів французький учений Ш.Ерміт в 1873 році, а у 1882 році професор Мюнхенського університету Карл Луіз Фердінанд Ліндеман (1852–1939) використовуючи результати, отримані французьким математиком Ш.Ермітом, довів, що  – число трансцендентне, тобто воно не є коренем ніякого алгебраїчного рівняння a>n>xn + a>n–>>1>xn–1+ … + a>1>x + a>0> = 0 с цілими коефіцієнтами. Цей доказ поставив крапку в історії найдавнішої математичної задачі „про квадратуру кола”. Тисячоріччя ця задача не піддавалася зусиллям математиків, вираження «квадратура кола» стало синонімом нерозв'язної проблеми. А вся справа виявилася в трансцендентній природі числа .

У даній курсовій роботі розглядається сучасні доведення ірраціональності і трансцендентності чисел π і е, а також розглядаються історичні та сучасні методи наближеного обчислення їх за допомогою рядів і за допомогою ланцюгових дробів.

РОЗДІЛ І

ОСОБЛИВІ ЧИСЛА МАТЕМАТИКИ „π” ТА „е”

1.1 Сутність та історична поява чисел „π” та „е”

Письмова історія числа  починається з єгипетського папірусу, датуємого приблизно 2000 роком до нашої ери, але воно було відомо ще древнім людям. Число  звернуло на себе увагу людей ще в ті часи, коли вони не вміли письмово викладати ні своїх знань, ні своїх переживань, ні своїх спогадів. З тих пір як перші натуральні числа 1,2,3,4,…стали нерозлучними супутниками людської думки, допомагаючи оцінювати кількості предметів або їхні довжини, площі або об'єми, люди познайомилися із числом . Тоді воно ще не позначалося однією з букв грецького алфавіту і його роль грало число 3. Неважко зрозуміти, чому числу  приділяли так багато уваги. Виражаючи величину відносини між довжиною окружності і її діаметром, воно з'явилося у всіх розрахунках пов'язаних із площею кругу або довжиною окружності. Але вже в далекій давнині математики досить швидко й не без подиву виявили, що число 3 не зовсім точно виражає те, що тепер відомо як число  (пі). Безумовно, до такого висновку могли прийти тільки після того, як до ряду натуральних чисел додалися дробові або раціональні числа. Так єгиптяни одержали результат: .. Індуси в VVI століттях користувалися числом ,, китайці числом , а ще [21].

Позначення числа  походить від грецького слова ("окружність"). Уперше це позначення використовував в 1706 році англійський математик У.Джонс, але загальноприйнятим воно стало після того, як його (починаючи з 1736 року) став систематично вживати Леонард Ойлер. У кінці 18 століття І.Ламберт і А.Лежандр установили, що  ірраціональне число, а у 1882 році Ф.Ліндеман довів, що воно трансцендентне, тобто не може задовольняти ніякому алгебраїчному рівнянню із цілими коефіцієнтами.

Протягом усього існування числа , аж до наших днів, велася своєрідна "погоня" за десятковими знаками числа . Леонардо Фібоначі близько 1220 року визначив три перші точні десяткові знаки числа . В 16 столітті Андріан Антонис визначив 6 таких знаків. Франсуа Вієтт (подібно Архімедові), обчислюючи периметри вписаних і описаного 322 216багатогранників, одержав 9 точних десяткових знаків. Андріан Ван Ромен таким же способом одержав 15 десяткових знаків, обчислюючи периметри 1 073 741 824багатогранників. Лудольф Ван Келень, обчислюючи периметри 32 512 254 720багатогранників, одержав 20 точних десяткових знаків. Авраам Шарп одержав 72 точних десяткових знаків числа . В 1844 році З.Дазе обчислює 200 знаків після коми числа , в 1847 році Т.Клаузен одержує 248 знаків, в1853 Ріхтер обчислює 330 знаків, у тім же 1853 року 440 знаків одержує З.Дазе, а у цьому ж році У.Шенкс одержує 513 знаків. З появою ЕОМ кількість вірних знаків десяткових знаків різко зростає [21]:

1949 рік — 2 037 десяткових знаків (Джон фон Нейман, ENIAC),

1958 рік — 10 000 десяткових знаків (Ф.Женюи, IBM704),

1961 рік — 100 000 десяткових знаків (Д.Шенкс, IBM7090),

1973 рік — 10 000 000 десяткових знаків (Ж.Гийу, М.Буйе, CDC7600),

1986 рік — 29 360 000 десяткових знаків (Д.Бейли, Cray2),

1987 рік — 134 217 000 десяткових знаків (Я.Канада, NEC SX2),

1989 рік — 1 011 196 691 десяткових знаків (Д.Гудновски й Г.Гудновски, Cray2+IBM3040)"

При обчисленні вірних десяткових знаків числа  користувалися різними способами, деякі, як і Архімед обчислювали периметри вписаних і описаних nбагатогранників, але пізніше стали вдаватися до допомоги рядів. Так Лейбниц обчислював  за допомогою ряду [26]:

Шарп застосував ряд [21]:

Л.Ойлер за допомогою ряду [24]:

Джон Валлис ( 16161703) знайшов нескінченний добуток, за допомогою якого можна обчислити число  (пі), у вигляді [25]:

Число́ пі (позначається ) –математично визначається в Евклідовій геометрії як відношення довжини кола до його діаметру .

Грецька літера пі.

або як площа круга одиничного радіусу.

Довжина кола дорівнює , якщо його діаметр 1

Рис.1.1. Геометричне трактування числа

Історія числа е (основа експонентної функції).

e — математична константа, основа натурального логарифма, трансцендентне число. Іноді число e називають числом Ойлера або числом Непера [22]. Позначається рядковою латинською буквою «e». Чисельне значення:

e = 2,718 281 828 459 045 235 360 287 471 352 662 497 757

Число e може бути визначено декількома способами [22].

    Через бескінечну межу:

(друга чудова межа).

Як сума ряду:

або .

Як єдине число a, для якого виконується

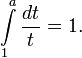
Як єдине позитивне число a, для якого вірно (похідна функції дорівнює самій функції)

Число з'явилося порівняно недавно. Його іноді називають "неперовим числом" на честь винахідника логарифмів шотландського математика Джона Непера ( 15501617) [22], однак це необґрунтовано, тому що немає твердих підстав для твердження, що Непер мав про число е чітке позначення. Уперше математично обгрунтоване позначення числа "е" увів Леонард Ойлер (17071783). Він також обчислив точні 23 десяткові знака цього числа після коми, використавши подання числа е у вигляді нескінченного числового ряду [24]:

,

отримане Данилом Бернулі( 17001782). В 1873 році Ерміт довів трансцендентність числа е. Л.Ойлер одержав чудовий результат, що зв'язує числа е,  :

Йому належить і заслуга визначення функції для комплексних значень z, що поклало початок математичному аналізу в комплексній області теорії функцій комплексного змінного. Ойлером були отримані наступні формули:

Клас логарифмів по основі е, називаються натуральними й позначаються як . Експоненціальна функція з основою е має особливий характер – всі похідні функції дорівнюють самій функції:

1.2 Визначення понять ірраціональності та трансцендентності чисел

Для того щоб довести ірраціональність і транcцендентність чисел і 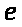приведемо з початку деякі визначення, теореми й приклади ірраціональних і трансцендентних чисел [9], [11], [20].

Множина дійсних чисел містить у собі підмножину всіх раціональних чисел, тобто чисел, які можна представити у вигляді кінечного дробу, а всі інші дійсні числа називають ірраціональними.

Означення 1.2.1. Дійсне число називається ірраціональним, якщо воно відмінно від всіх раціональних чисел, тобто якщо при всіх цілих і .

Існування ірраціональних чисел було доведено ще грецькими математиками. Ірраціональність числа була відома ще в V столітті до нашої ери математикам пифагорівскої школи, а доказ цього часто приписується Піфагору, хоча точно невідомо, чи було воно побудовано їм самим або кимнебудь із його учнів. Оскільки множину всіх раціональних чисел можна обчислити, основну масу дійсних чисел становлять ірраціональні числа.

Розглянемо найпростіші методи, які дозволяють установлювати ірраціональність деяких класів чисел. На перший погляд здається невиправданим те, що задача доказу ірраціональності якогонебудь дійсного числа а ставиться до теорії чисел, однак включення такої проблематики в теорію чисел стає відразу ясним, якщо поставити це питання в наступній формі: довести, що не існує цілих чисел і , таких, що .

Дамо спочатку одну теорему, що встановлює ірраціональність досить широкого класу дійсних чисел, які зустрічаються особливо часто в шкільних курсах алгебри й геометрії.

Теорема 1.2.1 Нехай багаточлен із цілими коефіцієнтами, дійсне число корінь . Тоді або ціле, або ірраціональне число.

Доведення. 0ціле число, тому ми розглянемо тільки випадок . Припустимо, що не є ірраціональним числом , тобто що раціональне число де й цілі , . Підставляючи в рівняння й домножуючи обидві частини його на , одержуємо:

Із цього співвідношення безпосередньо видно, що є дільником (позначається, як ). Оскільки , то умови й можуть бути тільки при , тобто ціле.

Приклад 1.2.1 Якщо натуральне число відмінно від всіх степеней цілих чисел, то ірраціональне число.

Дійсно, є корінь рівняння . Якщо число не є цілим, то згідно теореми 1.2.1. воно ірраціональне. Наприклад ірраціональне число, тому що послідовність квадратів цілих чисел має вигляд 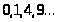і жоден із цих квадратів не дорівнює . Число ірраціональне , тому що послідовність позитивних кубів цілих чисел має вигляд і жоден з них не дорівнює .

Ірраціональність деяких дійсних числі можна встановити за допомогою критеріїв, сформульованих у наступних двох теоремах.

Теорема 1.2.2. Якщо раціональне число, то існує таке що для будьякого раціонального дробу буде справедлива нерівність :

(1.2.1)

Доведення. Нехай , де .Візьмемо . Для будьякого раціонального дробу буде >, >а отже, ціле число , і тоді

Теорема 1.2.3.Якщо для будьякого позитивного числа існує хоча б одна пара цілих чисел , таких ,що то ірраціональне число.

(1.2.2)

Доведення. Якби було раціональним, то по теоремі (1.2.2) найшлося б , таке, що для будьякого дробу виконувалася б нерівність (1.2.1), а це суперечить тому, що відповідно до наших умов для цього існує таке, що має місце нерівність (1.2.2). Припущення, що раціональне число, привело нас до протиріччя, значить ірраціональне.

Приклад 1.2.2. Довести ірраціональність числа :

Візьмемо довільне й виберемо настільки великим, щоб було .Покладемо,

, .

і цілі числа . При таких і

,

так, що ірраціональне.

Теорема 1.2.4. Якщо при деякому розкладанні в систематичний дріб з підставою системи числення рівним , містить як завгодно довгі кінцеві ланцюжки , що складаються з однієї й тої ж цифри, то ірраціональне число.

Інакше кажучи , якщо в розкладанні

для кожного найдуться , причому й , те ірраціональне.

Доведення. Якби було раціональним, то розкладання в систематичний дріб з підставою було б періодичним. Таке розкладання не може мати однієї цифри в періоді, тому що для незліченної множини . Припущення ж, що період складається з декількох цифр, також суперечить нашим умовам , тому що в цьому випадку не могли б існувати ланцюжка з однієї цифри довжиною більше, ніж число цифр у періоді.

Приклад 1.2.3.Число , записуєме в десятковій системі счислення у вигляді

іраціональне.

Введемо визначення трансцендентності чисел.

Означення 1.2.2 Будьяке неалгебраїчне число називається трансцендентним.

Таким чином, називається трансцендентним числом, якщо не існує жодного багаточлена із цілими коефіцієнтами, коренем якого є , тобто для всіх , при будьякому комплексі цілих, не рівних одночасно нулю чисел маємо

1.3 Доведення ірраціональності та трансцендентності числа „π”

Доведемо ірраціональність і транcцендентність числа .

Теорема 1.3.1.Число ірраціональне.

Доведення. Припустимо, що раціонально, тобто , де й натуральні числа. При збільшенні величина ; тому можна знайти таке . що виконується нерівність

(1.3.1)

Розглянемо для такого функцію

(1.3.2)

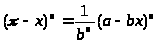Заміняючи через і розкладаючи по ступенях , можна представити у вигляді:

(1.3.3)

так що . Якщо рівність 1.3.3 продифференціювати разів, де , то одержимо:

Біноміальний коэфициент ціле число, так що цілі числа.

З рівності 1.3.2 видно, що , так що диференцируючи, одержуємо для всіх

, і отже,

, цілі числа.

Інтегруючи вроздріб, одержуємо:

(1.3.4)

тому що наступна похідна тотожно дорівнює нулю.

З рівності (1.3.4) одержуємо:

(1.3.5)

де ціле число.

Оскільки в інтервалі подінтегральна функція позитивна, то інтеграл у лівій частині (1.3.5) більше нуля й . З іншого боку, з рівності (1.3.2) видно, що при маємо:

і оскільки , то при нашім виборі маємо:

тобто .

Припущення, що раціонально, привело нас до протиріччя, отже , ірраціональне.

Теорема доведена.

Ірраціональність числа була доведена вперше в 1761 році французьким математиком Ламбертом. Доказ Ламберта заснований на застосуванні безперервних дробів.

π — трансцендентне число, це означає, що воно не може бути коренем багаточлена із цілими коефіцієнтами. Трансцендентність числа π була доведена в 1882 році професором Кьонінгзбергського, а пізніше Мюнхенського університету Ліндеманом. Доказ спростив Феликс Клейн в 1894 році.

Для того щоб довести трансцендентність числа π доведемо спочатку три допоміжних твердження.

Лема 1.3.1. При будьякому цілому позитивному й будьякому , має місце рівність

(1.3.6)

де

Доведення. Скористаємося розкладанням функції в ряд

Із цього розкладання треба, щоб

де

Тому що

Лема доведена.

Лема 1.3.2 Нехай

де

Тоді

(1.3.7)

де

(1.3.8)

(1.3.9)

Покладаючи в рівності (1.3.6) , одержимо

Помноживши ці рівності, відповідно, на й склавши, одержимо рівність (1.3.7).

Лема 1.3.3. Сума й добуток двох алгебраїчних чисел є числами алгебраїчними (і притім цілими алгебраїчними, якщо такими є доданки й множники).

Доведення. Дійсно нехай алгебраїчне число, що є коренем рівняння ого ступеня з раціональними коефіцієнтами й інших корінів цього рівняння й нехай – алгебраїчне число , що є коренем рівняння ой ступеня з раціональними коефіцієнтами , а – інших корінів цього рівняння.

Добуток всіх різниць виду, мабуть, є багаточленом, одним з корінів якого є . Отже, нам досить переконатися в тім, що коефіцієнти цього багаточлена суть раціональні числа. Але ці коефіцієнти суть симетричні функції від аргументів і аргументів . Застосовуючи двічі теорему про симетрію функції (“Якщо симетрична функція є багаточленом і корінь рівняння те де багаточлен. Зокрема, якщо коефіцієнти багаточлена цілі числа , то коефіцієнти багаточлена теж цілі числа ” [9], ми переконаємося в справедливості нашого твердження про добуток алгебраїчних чисел. Аналогічно доводиться твердження про суму

Тепер перейдемо до доказу самої теореми, що транcцендентне число.

Теорема. транcцендентне число.

Доведення. Нехай алгебраїчне число . На підставі леми 1.3.3 число теж алгебраїчне й отже, є корнем рівняння виду

(1.3.10)

з цілими коефіцієнтами. Нехай корінь цього рівняння , одним з них є . Тому що , то

(1.3.11)

Розкривши дужки в лівій частині цієї рівності , одержимо

(1.3.12)

Позначимо через ті з показників, які відмінні від нуля , а через інші. Приєднавши відповідні доданки в лівій частині (1.3.12) до першого, можемо записати рівність (1.3.12) у вигляді

(1.3.13)

де ціле позитивне число.

Числа суть цілі алгебраїчні числа, тому згідно лемі (1.3.3) цілими алгебраїчними числами є й числа

Дуже важливо помітити , що якщо симетричний багаточлен із цілими коефіцієнтами , те ціле число

Дійсно, якщо

то буде також

тому що кожна із сум, що коштують у правій частині другої рівності, відрізняється від відповідної суми першої рівності, що складаються або рівними або утримуючого цього числа як множники, а числа дорівнюють нулю.

Вираз в правій частині останньої рівності є симетричним багаточленом відносно й отже , відносно . На підставі теореми [20]: “Якщо симетричний багаточлен із цілими коефіцієнтами й корінь уранения із цілими коефіцієнтами, тj ціле число ” , треба, щоб було цілим числом.

Покладемо в рівності (1.3.7) , послідовно , і складемо результати , помноживши попередньо перші з них на .Одержимо на підставі (1.3.13)

(1.3.14)

Якщо ми доведемо, що для деякого багаточлена рівність (1.3.14) неможлива, якщо алгебраїчні числа, то тим самим буде доведена трансцендентність .

Покладемо

(1.3.15)

де просте число, що залишається поки невизначеним. Багаточлен (1.3.15) можна представити у видах

(1.3.16)

Перше з рівностей (1.3.16) безпосередньо отримане з рівності (1.3.15), якщо в правій його частині розкрити дужки. При цьому одержимо

Добуток у правій частині симетричний й тому ціле число. Такі ж, легко зміркувати є й числа .

Друге з рівностей (1.3.16) виходить із рівності (1.3.15) якщо записати його у вигляді

і звільнитися від квадратних дужок. Аналогічно виходить третє з рівностей (1.3.16) і так далі. Важливо помітити, що …є багаточленами із цілими коефіцієнтами відносно

Легко підрахувати, що

(1.3.17)

(1.3.18)

Сума

є симетричним багаточленом із цілими коефіцієнтами й тому є цілим числом. Це число, через (1.3.13) , ділиться на .

Ми будемо вважати більшим кожного із цілих чисел . Тоді

буде цілим числом, яке не ділится на , тому що таким буде перший доданок у правій частині, у той час, як інші доданки будуть цілими числами, що діляться на . Таким чином, сума, що визначена в першій частині рівності (1.3.14), при нашому виборі числа , є цілим числом, що не ділиться на , тобто є відмінним від нуля цілим числом.

Повернемося до розгляду суми

З рівності (1.3.9) , першої рівності (1.3.16) і того , що

легко доглянути, що буде по модулі меншим одиниці, при досить великому .

Таким чином, права частина рівності (1.3.14) є сумою цілого, відмінного від нуля, числа й числа, по модулі меншого одиниці. Така сума не може рівнятися нулю й тому рівності (1.3.14), при нашім виборі й , неможливі. Цим і завершений доказ трансцендентності числа .

Теорема доведена.

1.4 Доведення ірраціональності та трансцендентності числа „е”

Доведемо ірраціональність і трансцендентність числа .

Теорема 1.4.1.Число ірраціональне.

Доведення. Припустимо, що , де й натуральні числа.Відомо, що

Із треба, що () – було ціле число, тоді цілим буде й число [9]

Ми одержуємо звідси ,

Тобто між 0 і 1 лежить ціле число. Припущення, що раціональне, привело нас до протиріччя, значить ірраціональне.

Теорема доведена.

Другий шлях доказу ірраціональності e [23].

Припустимо, що раціонально. Тоді , де  — ціле, а  — натуральне, звідки

Множачи обидві частини рівняння на , одержуємо

Переносимо в ліву частину:

Всі доданки правої частини цілі, отже:

 — ціле

Але з іншої сторони

Знов одержуємо протиріччя.

Трансцендентність була доведена тільки в 1873 році французьким математиком Шарлем Ермітом [22].

Теорема 1.4.2. Число трансцендентно.

Доведення. Припустимо, що корінь багаточлена із цілими коефіцієнтами так що

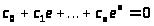(1.4.1)

Позначимо через найбільшу з абсолютних величин коефіцієнтів , так що при всіх маємо .

При заданому функція при збільшенні прагне до нуля й, оскільки існують які завгодно більші прості числа, ми можемо вибрати просте число так , що будуть одночасно виконуватися умови:

Розглянемо функцію ступеня

Інтегруючи вроздріб , знаходь :

Продовжимо цей процес, поки не дійдемо до похідної порядку , рівної тотожно нулю. Одержимо :

(1.4.2)

де ( до похідної порядку ).

Підставляючи в (1.4.2) замість число й множачи на ,, маємо:

(1.4.3)

Надаючи значення та складаючи при рівності (1.4.3) і беручи до уваги , що через тотожність (1.4.2) права частина виходить рівною нулю, знаходимо:

(1.4.4)

Розкладання по ступенях має вигляд :

, (1.4.5)

де цілі числа. Одержуємо:

,

а є ціле число, оскільки просте й , не ділиться на ;

, як легко бачити з (1.4.4), цілі числа, що діляться на ;

являє собою суму цілого числа , що не ділиться на , і інші цілі числа, кратні , так що не є дільником. Оскільки , те буде також не є дільником .

Розкладання по ступенях , де , має вигляд

(1.4.6)

де всі коефіцієнти цілі числа.

Диференціюючи (1.4.6), легко бачити, що при всіх таких :

ціле число , що ділиться на .

У сумі

перший доданок не ділиться на , а всі інші доданки діляться на , так що ціле число , що не ділиться на , і , таким чином, відмінне від нуля.

Ціле число, відмінне від нуля, має модуль, більший або дорівнюючий одиниці, так що .

Оцінимо тепер величину зверху. Згідно (1.4.4.):

У всіх інтегралах, що входять в , величина пробігає значення, що не виходять за межі сегмента , а при таких справедлива нерівність:

так , що при всіх маємо

що суперечить отриманій раніше нерівності .

Таким чином, припущення, що алгебраїчне число, привело нас до протиріччя; отже, неалгебраїчне число, тобто трансцендентне число.

Теорема доведена.

РОЗДІЛ ІІ

НАБЛИЖЕНЕ ОБЧИСЛЕННЯ ЧИСЛА „π”

2.1 Методи наближеного обчислення числа „π” за допомогою числових рядів

Число з'являється не тільки при рішенні геометричних задач. Із часу Ф.Віета (1540–1603) розвідка меж деяких арифметичних послідовностей, що встановлені простими законами, приводило до того ж числа . У зв'язку із цим у визначенні числа брали участь майже всі відомі математики: Ф.Віет, Х.Гюйгенс, Дж.Валліс, Г.В.Лейбніц, Л.Ойлер [21]. Вони одержували різні вирази для у вигляді нескінченного добутку, суми ряду, нескінченного дробу.

Наприклад, в 1593 Ф.Виет (15401603) вивів формулу [21]

В 1665 Джон Валліс (16161703) довів, що [21]

,

Або

.

Ця формула має його ім'я. Для практичного знаходження числа вона мало придатна, але корисна в різних теоретичних міркуваннях. В історію науки вона ввійшла як один з перших прикладів нескінченних добутків.

Готфрид Вільгельм Лейбниц (16461716) в 1673 установив наступну формулу [21]:

яка представляє число /4 як суму ряду. Однак цей ряд сходиться дуже повільно. Щоб обчислити з точністю до десяти знаків, треба було б, як показав Ісаак Ньютон, знайти суму 5 млрд чисел і затратити на це біля тисячі років безперервної роботи.

Леонарду Ойлеру належать і інші гарні формули рядів повільної східності, що включають [21]:

,

,

.

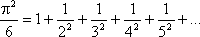В останній формулі в чисельнику розташовані всі прості числа, а знаменники відрізняються від них на одиницю, причому знаменник більше чисельника, якщо той має вигляд 4n + 1, і менше в противному випадку.

Лондонський математик Джон Мэчин (16801751) в 1706, застосовуючи формулу [21]

одержав вираження

arctg 1 = 4 arctg – arctg .

Підстановка в нього arctg 1 = і рядів для arctg x

(arctg x = ) приводить до формули

,

яка дотепер уважається однієї із кращих для наближеного обчислення . Щоб знайти ті ж десять точних десяткових знаків, буде потрібно всього кілька годин ручного рахунку. Сам Джон Мэчин обчислив з 100 вірними знаками.

Скористаємося відомим рядом для арктангенса [21]:

(2.1.1)

Якщо взяти, то , і ми одержимо ряд

(2.1.2)

уже придатний для обчислення/

Скористаємось формулою додавання для арктангенса

(2.1.3)

і вибираючи в якості і якінебудь два правильні дроби , що задовольняють співвідношенню

або (2.1.4)

будемо мати

(2.1.5)

Наприклад, поклавши , одержимо ряд

(2.1.6)

Існують, однак, ряди, ще більш ефективні для розрахунку числа .

Покладемо тоді

Через близькість цього числа до , ясно, що кут близький до .

Поклавши:

, будемо мати :

так що

Звідси

це формула Мєшина (J.Machin).

Обчислимо по ній число з 7ю знаками після коми. Для цього досить тих членів формули, які фактично виписані. Тому що обидва ряди – типу рядів Лейбниця, то виправлення в зменшуваному й від'ємнику на відкидання невиписаних членів, відповідно, будуть:

і

Збережені члени (2.6) перетворимо у десяткові дроби, округляючи їх ( за правилом доповнення ) на восьмому знаку. Обчислення зведені в таблицю ( у дужках указує знак виправлення):

З огляду на всі виправлення, маємо:

так що

Отже , остаточно причому всі виписані знаки вірні.

C допомогою того ж ряду для arctg x і формули

 = 24 arctg + 8 arctg + 4 arctg

значення числа було отримано на ЕОМ з точністю до ста тисяч десяткових знаків. Такого роду обчислення становлять інтерес у зв'язку з поняттям випадкових і псевдовипадкових чисел. Статистична обробка впорядкованої сукупності зазначеної кількості знаків показує, що вона має багато рис випадкової послідовності. А так виглядає 101 знак числа без округлення:

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679.

2.2 Методи наближеного обчислення числа „π” за допомогою розкладу в нескінченні ланцюгові дроби

Згідно [2] для наближеного розрахунку числа  побудований наступний ланцюговий дріб:

(2.2.1)

(послідовність неповних часток така: 3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1, 15, 3, 13,...)

Знайдемо підходящі для практичних розрахунків дроби використовуючи вищенаведений ланцюговий дроб:

а потім складемо таблицю для обчислення наступних дробів за допомогою рекуррентного правила:

Степінь дробу (за числом в ланцюгі)

3 (1)

7(2)

15(3)

1(4)

Чисельник дробу

3

22

333

355

Знаменник дробу

1

7

106

113

Одержуємо підходящі дроби й . Наближення , рівне , було відомо ще Архімедові [21], а наближенням користувався Андріан Меций ще наприкінці 16 сторіччя [21] . Перше наближення дуже зручно тим, що знаменник 7 дуже невеликий.У другому дробі при порівняно невеликому знаменнику виходить наближене значення з високою точністю.

Щоб оцінити цю точність, використовуємо формулу [4]

(2.2.2)

У нашім випадку , а

Виходить,

тобто точність отриманої відповіді перевищує . Обертаючи дріб у десятковий, одержуємо:

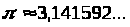
РОЗДІЛ ІІІ

НАБЛИЖЕНЕ ОБЧИСЛЕННЯ ЧИСЛА „е”

3.1 Методи наближеного обчислення числа „е” за допомогою числових рядів

Обчислимо число з точністю до з використанням ряду [20]. Запишемо ряд для :

(3.1.1)

Ця рівність має місце для кожного . При

(3.1.2)

Насамперед установимо, яким треба взяти число для здійснення необхідної точності. Якщо покласти наближене , то помилка буде

тому що є прогресія, знаменник якої дорівнює (сума прогресси дорівнює , де її перший член, а знаменник).

Для здійснення необхідної точності треба, щоб , тобто . Уже при дана нерівність задовольняється , тому що . Але тому що обіг членів розкладання для в десятковий дріб і при цьому їхнє округлення послужить джерелом нової погрішності, то в запас точності візьмемо .

Оборотні члени розкладання в десятковий дріб використовуємо, округляючи їх за правилом доповнення на сьомому знаку. Тоді похибка кожного члена по абсолютній величині не більше , а вся похибка – не більше , тому що перші три члени розкладання обчислюються точно , і будемо мати:

таким чином, похибка на відкидання всіх членів розкладання, починаючи з (дванадцятий член розкладання), не перевершує , а похибка на округлення не більше . Звідси виходить, що загальна погрішність за абсолютним значенням дорівнює сумі

Але тоді число знаходиться між числами й , тобто . Отже, можна покласти . Значення з 19 знаками після коми є [22]:

3.2 Методи наближеного обчислення числа „е” за допомогою розкладу в нескінченні ланцюгові дроби

Згідно [9] для наближеного розрахунку числа побудований наступний ланцюговий дріб.

Теорема 3.2.1

(3.2.1)

Доведення . Визначимо як суму ряду:

.

Цей ряд сходиться при будьяких значеннях ; однак ми будемо розглядати тільки значення , що лежать в інтервалі .

Легко перевірити , що має місце тотожність

(3.2.2)

Дійсно, коефіцієнт при в лівій частині рівності (3.2.2) дорівнює

а в правій частині рівності (3.2.2) він дорівнює

,

так що (3.2.2) вірне.

Позначимо через . Зокрема, оскільки

То

З тотожності рівності (3.2.1) при одержуємо:

(3.2.3)

Оскільки позитивно, рівність (3.2.3) показує , що при всіх

, , тобто й послідовність співвідношень (3.2.2) при

дає розкладання в ланцюговий дріб:

(3.2.4)

Теорема доведена.

Тепер розкладемо в ланцюговий дріб число [2].

Теорема.3.2.2

(3.2.5)

(послідовність неповних часток така: 2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 14, 1, 1, 16, 1,...) , тобто елементи розкладання в ланцюговий дріб мають вигляд:

Доведення. Позначимо підходящі дроби до правої частини (3.2.4) через , а підходящі дроби до (3.2.3) через . Доведемо , що

Беручи до уваги значення елементів ланцюгового дробу (3.2.4) , маємо:

Звідки знаходимо:

Аналогічне співвідношення маємо й для , так що

(3.2.6)

Доведемо індукцією по , що

(3.2.7)

З (3.2.3) і ( 3.2.4) безпосередньо обчислюємо , так що співвідношення (3.2.7) вірно для всіх з номерами, меншими ніж , де , тобто зокрема

тоді , використовуючи рівності (3.2.6) , одержуємо:

Згідно за принципом повної математичної індукції равенство (3.2.6) вірно для всіх .

Зовсім аналогічно доводиться, що

Розглядаючи тепер межу відносини величин і , знаходимо:

тобто

Оскільки ланцюговий дріб у правій частині (3.2.5) сходиться, ми будемо мати також, що взагалі, а це доводить теорему.

Теорема доведена.

ВИСНОВКИ

У даній роботі було викладено суть і історичне поява чисел і .Так само були уведені поняття ірраціональних і трансцендентних чисел.

Число – відношення довжини окружності до її діаметра, – величина постійна й не залежить від розмірів окружності. Число, що виражає це відношення, прийнято позначати грецькою буквою (від «perijereia» – окружність, периферія). Це позначення стало вживаним після роботи Леонарда Ойлера, що ставиться до 1736, однак уперше воно було вжито Вільямом Джонсом (16751749) в 1706. Як і всяке ірраціональне число, воно представляється нескінченним неперіодичним десятковим дробом: = 3,141592653589793238462643… Потреби практичних розрахунків, що ставляться до окружностей і круглих тіл, змусили вже в далекій давнині шукати для наближень за допомогою раціональних чисел.

У даній роботі ми довели ірраціональність і трансцендентність чисел і . Так само ми показали як можна розкласти числа й за допомогою ряду й за допомогою ланцюгового дробу.

Нескінченні ланцюгові дроби можуть бути використані для рішення алгебраїчних і трансцендентних рівнянь, для швидкого обчислення значень окремих функцій.

Математиками виведена формула, яка пов’язує числа е и π, т. н. «інтеграл Пуассона» або «інтеграл Гаусса»

доводячи світове значення чисел е и π, на основі яких описуються процеси у багатьох науках та природних явищах.

У сучасності ланцюгові дроби знаходять все більше застосування в обчислювальній техніці, тому що дозволяють будувати ефективні алгоритми для рішення ряду задач на ЕОМ.

Так, дуже швидко працюють обчислювальні алгоритми, засновані на формулах Рамануджана

і братів Чудновських

В 1997 році Дейвід Х. Бейлі, Пітер Боруейн і Саймон Плуфф відкрили спосіб швидкого обчислення довільної двійкової цифри числа π без обчислення попередніх цифр, заснований на формулі

Невирішені проблеми сучасної математики у розділі теорії чисел:

Невідомо, чи є числа π і e алгебраїчно незалежними;

Невідомо, чи є суми та комбінації чисел: π + e, π − e, πe, π / e, πe, ππ трансцендентними;

Дотепер нічого не відомо про нормальність числа ; невідомо навіть, які із цифр 09 зустрічаються в десятковому поданні числа  нескінченну кількість разів.

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

1. Арнольд И.В. Теория чисел. М.: Учпедгиз, 1939. 287 с.

2. Арнольд В.И. Цепные дроби. М.: МЦМНО, 2000. 40 с.

3. Ангилейко И.М. Бесконечные ряды. – Минск: Издво „Высшая школа”, 1964 – 143 с.

4. Бескид Н.М. Цепные дроби // Научнопопулярный журнал „Квант”. М.:МЦМНО, № 1, 1970

5. Беркович Е. Мировые константы π и e в природе // Журнал «7 искусств», № 1, декабрь 2009 – http://7iskusstv.com, 2010

6. Болтянский В. Экспонента // Научнопопулярный журнал „Квант”. М.:МЦМНО, № 3, 1984

7. Бородін О.І. Теорія чисел.К.: Радянська школа, 1965. 262 с.

8. Бохан К.А. и др. Курс математического анализа т.II. М.: Просвещение 1972.

9. Бухштаб А.А. Теория чисел. М.: Просвещение, 1966. – 384 с.

10. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Издво „Наука” – „Физматлит”, 1979. – 664 с.

11. Дринфельд Г.И. Трансцендентность чисел  и e Харьков, Издательство Харьковского госуниверситета, 1952. – 79 с.

12. Звонкин А. Что такое  // Научнопопулярный журнал „Квант”. М.:МЦМНО, № 11, 1978

13. Канторович А.В.,Крылов В.И. Приближенные методы высшего анализа. М.: Изд. Физикоматематической литературы, 1962. 708 с.

14. Крылов В.И. Вычислительные методы : учебное пособие / В.И.Крылов, В.В.Бобков, П.И.Монастырный. – М.: „Наука”, 1976. Т.1. – 304 с.

15. Крылов В.И. Вычислительные методы : учебное пособие / В.И.Крылов, В.В.Бобков, П.И.Монастырный. – М.: „Наука”, 1977. Т.2. – 399 с.

16. Кузьмин Е., Ширшов А. О числе е. // Научнопопулярный журнал „Квант”. М.:МЦМНО, № 8, 1979

17. Кымпан Ф. История числа . М.: Наука, Гл. ред. физ.мат. лит.,1987. – 239 с.

18. Марков А. Доказательство трансцендентности числа  (невозможность квадратуры круга) Санкт Петербург, Типография Императорской академии наук, 1883. – 74 с.

19. Марчук Г.И. Методы вычислительной математики. Схемы, таблицы. – М.: « Наука», 1977. 456 с.

    Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. – М.: „Наука”, 1970. – Т.2. – 800 с.

    http://ru.wikipedia.org/wiki/Пи _Число математическая константа, выражающая отношение длины окружности к длине её диаметра, 2010

    http://ru.wikipedia.org/wiki/e_Число математическая константа, основание натурального логарифма, трансцендентное число. 2010

    http://www.new_numerolog.ru Трансцендентные числа е и пи,2010

    http://ru.wikipedia.org/wiki Ленард Эйлер, математик, 2010

    http://ru.wikipedia.org/wiki Джон Валлис, математик, 2010

    http://ru.wikipedia.org/wiki Лейбниц та ряди, математик, 2010

    http://formula.co.ua/blog/about Число пі, 2010