Теория случайных функций (работа 2)
Московский Государственный Институт Электроники и Математики
(Технический Университет)
КОНТРОЛЬНАЯ РАБОТА
по теме “Теория случайных функций“
Студент: Айдаров Д.А.
Вариант: 2.4.5.б
Преподаватель: Попка А.И.
Шымкент 2009
Дано: Восстанавливаемая, резервированная система (5,1) с КПУ, вероятность срабатывания КПУравна .
Время невыхода из строя (т.е. безотказной работы) основного элемента распределено экспоненциально с параметром .
Время восстановления вышедшего из строя элемента распределено экспоненциально с параметром .
Тип резервирования - ненагруженный.
Для описания состояния системы введем двумерный случайный процесс (t) = ((t), (t)) с координатами, описывающими:
- функционирование элементов
(t) {0, 1, 2} - число неисправных элементов;
- функционирование КПУ
(t) {0,1} - 1 - 1, если исправен, 0 - если нет.
Так как времена безотказной работы и восстановления имеют экспоненциальное распределение, то в силу свойств экспоненциального распределения, получим, что (t) - однородный Марковский процесс.
Определим состояние отказа системы:
Система отказывает либо если переходит в состояние 2 процесса (t) (т.е. отказ какого-либо элемента при количестве резервных элементов, равным нулю), либо если находится в состоянии 0 процесса (t) (т.е. отказ какого-либо элемента и отказ КПУ).
Таким образом, можно построить граф состояний системы:
|
> |
|
> |
 >
>
|
|
-




















 П
П>
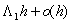 >
>
-
>
 >
>>
 >
>
0 - состояние, при котором 0 неисправных элементов, т.е. состояние (t) = (0, (t))
1 - состояние, при котором 1 неисправный элемент, т.е. состояние (t) = (1, 1)
П - состояние, при котором либо 2 неисправных элемента, либо 1 неисправный элемент и неисправный КПУ, т.е. композиция состояний (t) = (1, 1), (t) =(2, 0) - поглощающее состояние.
Найдем интенсивности переходов.
Так как выход из строя каждого из элементов - события независимые, то получим:
вероятность выхода из строя элемента: 1-exp(-5h) 5h + o(h)
вероятность восстановления элемента: 1-exp(-h) h + o(h)
>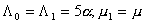 >
>
Пусть >
 >
>
Получим систему дифференциальных уравнений Колмогорова:
>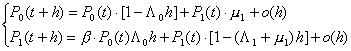 >
>
>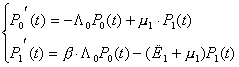 >
>
Пусть >
 >,
>,
т.е. применим преобразование
Лапласа к >
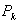 >.
>.
Т.к. >
 >,
то, подставляя значения интенсивностей,
получаем:
>,
то, подставляя значения интенсивностей,
получаем:
>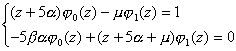 >
>
> >
>
> >
>
> >корни
>
>корни
>
 >
>
Представляя каждую из полученных функций в виде суммы двух правильных дробей, получаем:
> >
>
Применяя обратное преобразование
Лапласа, получаем выражения для функций
>
 >:>
>:> >
>
> >
>
Искомая вероятность невыхода системы из строя за время t:
> >
>
Где
> >,
>,
> >
>
Итак,
> >
>
Где
> >
>
Определим теперь среднее время жизни такой системы, т.е. MT (T - время жизни системы):
> >
>
>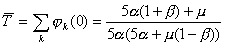 >
>
 >
> >
>