Линейная модель множественной регрессии (работа 1)
Задание 1
Линейная модель множественной регрессии ЛММР
Этап. Постановочный.
На постановочном этапе осуществляется определение конечных целей модели (прогноз, имитация, сценарий развития, управление) набор участвующих в ней факторов и показателей, их роль.
Пусть конечная цель модели - имитация поведения РТС индекса в зависимости цены акций.
Обозначим:
у - РТС индекс,
х1 - цена акции,
х2 - цена акции.
Этап. Априорный
На априорном этапе выполняется предметный анализ эконометрической сущности изучаемого явления, формирование и формализации априорной информации относящейся к природе исходных статистических данных и случайных составляющих.
Предмодельный анализ сущности изучаемого явления (используемой методики расчета РТС индекса), а также то, что обе акции входят в список, утвержденный для его расчета, позволяют сделать вывод о вероятности линейной зависимости поведения у от поведения х1 и х2.
Предположим, что х1 и х2 - неслучайные переменные, а у - случайная переменная.
Этап. Параметризация на этапе параметризация выполняется моделирование 3, т.е. выбор общей модели вида, состава, формы входящих в нее связей.
Анализ, проведенный на этапах 1,2 и сделанные предположения позволяют выбрать для наших целей модель вида:
В качестве рабочей гипотезы принимаем допущение о взаимности и гомоскедастичности регрессионных остатков l.
Этап. Информационный.
На информационном этапе выполняется сбор необходимой статистической информации, регистрация значений участвующих в модели факторов и показателей на различных временных и пространственных интервалах функционирования явления.
Наши данные приведены по итогам торгов в Российской торговой системе на 18.00 последовательно по датам торгов за октябрь 2003г. (данные с www.rbc.ru).
|
№ наблюдения |
Дата |
РТС индекс (посл) |
Цена акции ЛукОйл (посл), USD |
Цена акции НорНикель ГМК (посл), USD |
|
1 |
01.10 03 |
574,11 |
20,66 |
49,00 |
|
2 |
02.10 03 |
589,50 |
21,52 |
49,80 |
|
3 |
03.10.03 |
594,26 |
22,40 |
50,25 |
|
4 |
06.10.03 |
597,11 |
22,52 |
52,10 |
|
5 |
07.10.03 |
609,60 |
23,62 |
54,94 |
|
6 |
08.10.03 |
627,74 |
24,10 |
60,40 |
|
7 |
09.10.03 |
626,89 |
23,30 |
61,70 |
|
8 |
10.10.03 |
621,40 |
22,95 |
59,40 |
|
9 |
13.10.03 |
621,34 |
22,83 |
60,40 |
|
10 |
14.10 03 |
642,01 |
23,45 |
65,00 |
|
11 |
15.10.03 |
629,49 |
22,70 |
61,50 |
|
12 |
16.10.03 |
640,08 |
23,00 |
63,10 |
|
13 |
17.10.03 |
643,24 |
23,80 |
60,50 |
|
14 |
20.10.03 |
644,48 |
23,24 |
60,25 |
|
15 |
21.10 03 |
619,24 |
22,67 |
58,25 |
|
16 |
22.10 03 |
595,68 |
21,88 |
57,10 |
|
17 |
23.10.03 |
588,73 |
21,65 |
55,50 |
|
18 |
24.10 03 |
594,91 |
21,83 |
56,50 |
|
19 |
27.10.03 |
531,85 |
20,40 |
53,75 |
|
20 |
28.10.03 |
565,47 |
21,00 |
56,55 |
|
21 |
29.10.03 |
537,22 |
21, 20 |
55,95 |
|
22 |
30.10.03 |
512,37 |
19,25 |
53,00 |
|
23 |
31.10 03 |
508,94 |
20, 20 |
51,55 |
Визуальный анализ данных позволяет сделать вывод об изменении тенденции в рассматриваемом периоде. При графическом отображении значений РТС индекса данное изменение хорошо заметно:
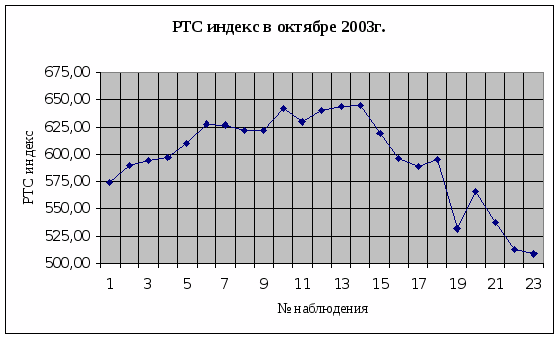
Построим, оценим качество и сравним графически три варианта модели:
по всей выборке,
за период возрастания индекса (первые 14 наблюдений),
за период убывания индекса (последние 10)
А также сделаем вывод о справедливости следующего априорного утверждения: модели 2,3 описывают исходные данные лучше, чем модель 1.
Этап. Идентификация модели
На этапе идентификации выполняется статистический анализ модели и, прежде всего статистическое оценивание неизвестных параметров.
В нашем случае имеется пространственная выборка объема k=23 (14 - для периода возрастания, 10 убывания). Число объясняющих переменных n=2. Матрица Х модели будет составлена из 3 столбцов размерности 23 (14,10) каждый. При этом в качестве первого столбца используется вектор из одних единиц, столбцы 2 - 3 представляют собой столбцы х1 и х2.
Подставляя соответствующие значения в формулу рассчитаем МНК - оценки для параметров А.
по всей выборке
|
23 |
510,1700 |
1306,5000 |
|
|
|
510,1700 |
11344,4995 |
29032,7645 |
|
1306,5000 |
29064,5645 |
74660,5000 |
|
Обратная |
16,9368 |
-0,6252 |
-0,0533 |
|
|
-0,8478 |
0,0549 |
-0,0065 |
|
0,0336 |
-0,0104 |
0,0035 |
|
13715,6600 |
|
|
|
305186,0672 |
|
781955,1640 |
|
-152,2248 |
|
|
А = |
33,8819 |
|
-0,0526 |
Y=-152,2248+33,8819*X1-0,0526*X2
за период возрастания индекса (первые 14 наблюдений)
|
14 |
320,0900 |
808,3500 |
|
|
|
320,0900 |
7329,1023 |
18527,9690 |
|
808,3500 |
18527,9690 |
47050,7575 |
|
Обратная |
58,3597 |
-3,1314 |
0,2305 |
|
|
-3,1314 |
0, 1983 |
-0,0243 |
|
0,2305 |
-0,0243 |
0,0056 |
|
8661,2500 |
|
|
|
198238,8637 |
|
501570,9840 |
|
295,8791 |
|
|
А= |
6,1272 |
|
3,1641 |
Y=295,8791+6,1272*X1+3,1641*X2
за период убывания индекса (последние 10)
|
10 |
213,3200 |
558,4000 |
|
|
|
213,3200 |
4563,2348 |
11936,8055 |
|
558,4000 |
11936,8055 |
31239,8050 |
|
Обратная |
56,1080 |
1, 1991 |
-1,4611 |
|
|
1, 1991 |
0,4902 |
-0, 2088 |
|
-1,4611 |
-0, 2088 |
0,1059 |
|
5698,8900 |
|
|
|
122039,6387 |
|
319214,1000 |
|
-309,1111 |
|
|
А = |
24,5941 |
|
6,3460 |
Y=-309,1111+24,5941*X1+6,3460*X2
Согласно первому уравнению, при увеличении цены акции ЛукОйл на 1 дол., РТС индекс возрастает на 33,8819 пункта; при увеличении цены акции НорНикель ГМК на 1 дол. уменьшится на 0,0526 пункта.
Согласно второму уравнению, при увеличении цены акции ЛукОйл на 1 дол., РТС индекс возрастет на 6,1272 пункта; при увеличении цены акции НорНикель ГМК на 1дол. возрастает на 3,1641 пункта.
Согласно третьему уравнению, при увеличении цены акции ЛукОйл на 1 дол., РТС индекс возрастет на 24,5941 пункта; при увеличении цены акции НорНикель ГМК на 1 дол. возрастает на 6,3460 пункта.
Этап. Верификация модели
На этапе верификации модели выполняется сопоставление модельных и реальных данных. Проверка адекватности модели, оценка точности модельных данных.
Проблема верификации заключается в решении вопроса о том, можно ли рассчитывать, что использование построенной модели даст результаты достаточно совпадающие с реальностью.
Наиболее распространенный подход верификации эконометрической модели - это ретроспективные расчеты.
Все исходные статистические данные за n - периодов времени делятся на две части:
обучающая выборка размерности n - j
экзаменующая выборка j
По данным обучающей выборки строится модель
С помощью модели осуществляется прогноз на j следующих периодов
Сравниваются прогнозные значения с реальными из экзаменующей выборки. Проводится анализ, оценивается точность
Проверка общего качества уравнения регрессии
Первый показатель - стандартная ошибка оценки Y.
Второй показатель - коэффициент детерминации, он характеризует долю общей вариации результирующего признака объясненную поведением выборочной функции регрессии.
При росте числа регрессоров значение R2 возрастает, однако качество описание исходных данных регрессионного уравнения может при этом не улучшиться, чтобы устранить этот подобный эффект проводят корректировку этого показателя на число регрессоров.
Проверка статистической значимости коэффициентов
Рассчитываются ошибки коэффициентов регрессии, для этого строятся ковариационные матрицы оценок. На главной диагонали матрицы стоят квадраты ошибок коэффициентов.
k - количество наблюдений
n - количество регрессий
Рассчитывается t - статистики Стьюдента
Определяется табличное значение t - статистики при числе степеней свободы k-n-1 и уровня значимости α/2. Сравнивается табличное и расчетное значение и делается вывод.
Далее рассчитаем показатели для оценки качества уравнений:
По всей выборке Y=-152,2248+33,8819*X1-0,0526*X2
|
k-n-1 |
20 |
|
Yср |
596,3330 |
|
σ2 - дисперсия |
312,1648 |
|
σ - станд. ош. |
17,6682 |
|
R2 |
0,8330 |
|
R2 кор. |
0,8163 |
|
5287,0816 |
-195,1602 |
-16,6290 |
|
|
С>А> = |
-264,6435 |
17,1410 |
-2,0345 |
|
10,5032 |
-3,2577 |
1,0872 |
|
бА0 = |
72,7123 |
tА0 = |
-2,0935 |
|
|
бА1 = |
4,1402 |
tА1 = |
8,1837 |
|
|
бА2 = |
1,0427 |
tА2 = |
-0,0504 |
По 14 наблюдениям Y=295,8791+6,1272*X1+3,1641*X2
|
k-n-1 |
11 |
|
Yср |
618,6607 |
|
σ2 - дисперсия |
51,3048 |
|
σ - станд. ош. |
7,1627 |
|
R2 |
0,9136 |
|
R2 кор. |
0,8979 |
|
2994,1340 |
-160,6574 |
11,8244 |
|
|
С>А> = |
-160,6574 |
10,1736 |
-1,2461 |
|
11,8244 |
-1,2461 |
0,2886 |
|
бА0 = |
54,7187 |
tА0 = |
5,4073 |
|
|
бА1 = |
3,1896 |
tА1 = |
1,9210 |
|
|
бА2 = |
0,5372 |
tА2 = |
5,8894 |
По 10 наблюдениям
Y=-309,1111+24,5941*X1+6,3460*X2
|
k-n-1 |
7 |
|
Yср |
569,8890 |
|
дисперсия |
192,9140 |
|
станд. Ош. |
13,8893 |
|
R2 |
0,9297 |
|
R2корр |
0,9096 |
|
10824,0152 |
231,3212 |
-281,8637 |
|
|
С>А> = |
231,3212 |
94,5720 |
-40,2710 |
|
-281,8637 |
-40,2710 |
20,4320 |
|
бА0 = |
104,0385273 |
tА0 = |
-2,9711 |
|
|
бА1 = |
9,724814036 |
tА1 = |
2,5290 |
|
|
бА2 = |
4,52017947 |
tА2 = |
1,4039 |
Проанализируем значения полученных показателей:
Значения R2 и R2 кор. близки к 1, т.е. качество подгонки хорошее.
Проверяя статистическую зависимость коэффициентов, проверяем гипотезу Н>0>: а>j> =0 (полученные коэффициенты статистически не значимы, их отличие от нуля случайно). Коэффициент а>j> значим (Н>0> отвергается). Если |t>A>расч|>tтабл. то гипотеза Н>0> отклоняется при значении а>j> не случайно отличается от нуля и сформировался под влиянием систематически действующего фактора.
Зададимся уровнем значимости 0,01, тогда при числе степеней свободы k-n-1=20 (11, 7 соответственно), табличное значение t - статистики Стьюдента t>0,005; 20>=2,845; t>0,005; 11>=3, 206; t>0,005; 7>=3,499.
Тогда при уровне значимости 0,01 (с вероятностью 0,99) статистически значимым являются (т.е. не случайно отличаются от 0, сформировались под влиянием систематически действующего фактора); в модели 1: а>0>, а>2>; в модели 2: а>0>, а>2>; в модели 3: а>0>, а>1>. (можно заметить, что для незначимых коэффициентов величина ошибки соответствующего коэффициента велика, превышает половину величины коэффициента).
Априорное утверждение относительно того, что модели 2 и 3 описывают исходные данные лучше, чем модель 1, подтвердилась. Действительно, значение R2 и R2кор. моделей 2 и 3 выше, чем модели 1, а стандартные ошибки оценки ниже. Вывод о справедливости утверждения можно сделать в результате сравнения соответствующих графиков.
Задание 2
Привести пример по одному примеру, иллюстрирующему практическое использование моделей каждого из следующих типов:
ЛММР
РМ с переменной структурой (фиктивные переменные)
Нелинейные РМ
Модели временных рядов
Системы линейных одновременных уравнений
1. ЛММР
Предположим, что по ряду регионов множественная регрессия величины импорта на определенный товар у относительно отечественного производства х>1>, изменения запасов х>2> и потребления на внутреннем рынке х>3> оказалась следующей
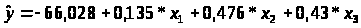
при этом среднее значение для рассматриваемых признаков составили
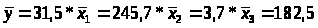
на основе данной информации могут быть найдены средние значения по совокупности показатели эластичности
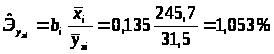
т.е. с ростом величины отечественного производства на 1% размер импорта в среднем по совокупности регионов возрастет на 1,053% при неизменных запасах и потребления семей.
2. РМ с переменной структурой (фиктивные переменные)
Проанализируем зависимость цен двухкомнатной квартиры от ее полезной площади. При этом в модель могут быть введены фиктивные переменные, отражающие тип дома: "хрущевка", панельный кирпичный.
При использовании трех категорий домов вводятся две фиктивные переменные: z>1> и z>2>.
Пусть переменная z>1> принимает значение 1 для панельного дома и 0 для всех типов домов; переменная z>2> принимает значение 1 для кирпичных домов и 0 для остальных; тогда переменные z>1> и z>2> принимают значение 0 для домов типа "хрущевки".
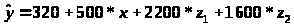
"хрущевки"
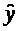=320+500*х
панельные
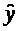=2520+500*х
кирпичные
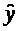=1920+500*х
В рассматриваемом примере за базу сравнения цены взяты дома "хрущевки" для которых z>1>= z>2>=0
Параметр при z>1>=2200 означает, что при одной и той же полезной площади квартиры цена ее в панельных домах в среднем на 2200 дол. выше чем в "хрущевках". Соответственно параметр при z>2> показывает, что в кирпичных домах цена выше в среднем на 1600дол. при неизменной величине полезной площади по сравнению указанным типам домов.
3. Нелинейные РМ
Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении эластичности спроса от цен широко используется степенная функция:
y=а*хb*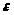
y - спрашиваемое количество,
xb - цена,
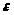- случайная ошибка.
4. Модели временных рядов
Имеются следующие данные о величине дохода на одного члена семьи и расходы на товар А.
|
Показатель |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
|
Расходы на товар А, руб. |
30 |
35 |
39 |
44 |
50 |
53 |
|
Доход на одного члена семьи, % к 1985г. |
100 |
103 |
105 |
104 |
115 |
118 |
Ежегодные абсолютные приросты определяем по формулам
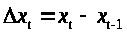
Расчеты можно представить в виде таблицы
-
y>t>
x>t>
30
-
100
-
35
5
103
3
39
4
105
2
44
5
104
4
50
6
115
6
53
3
118
5
Значение у не имеют четко выраженной тенденции они варьируют вокруг среднего уровня, что означает наличие в ряде динамики линейного тренда, аналогичный вывод можно сделать и по ряду х.
Системы линейных одновременных уравнений
Модель вида
y - валовый национальный доход
y>-1> - валовый национальный доход предшествующего года,
С - личное потребление,
D - конечный спрос (помимо личного потребления)
Информация за 9 лет о приросте всех показателей дана в таблице.
-
Год
D
y>-1>
У
С
1
-6,8
46,7
3,1
7,4
2
22,4
3,1
22,8
30,4
3
-17,3
22,8
7,8
1,3
4
12,0
7,8
21,4
8,7
5
5,9
21,4
17,8
25,8
6
44,7
17,8
37,2
8,6
7
23,1
37,2
35,7
30
8
51,2
35,7
46,6
31,4
9
32,3
46,6
56,0
39,1
ИТОГО
167,5
239,1
248,4
182,7
Для данной модели была получена система приведенных уравнений
