Дифференциальные уравнения с запаздывающим аргументом
1. Определения
Дифференциальные уравнения с запаздывающим аргументом вида
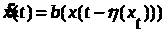 (1)
(1)
где
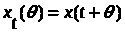 ,
,
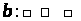 ,
,
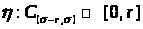 ,
называются дифференциальными уравнениями
с запаздыванием, зависящим от состояния,
а именно с сосредоточенным запаздыванием.
,
называются дифференциальными уравнениями
с запаздыванием, зависящим от состояния,
а именно с сосредоточенным запаздыванием.
Если заданы начальные данные в виде
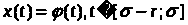 (2)
(2)
То имеет смысл определить понятие решения, начинающегося в точке σ с функции φ, или, короче, начинающегося в φ.
В дальнейшем будем рассматривать только решения, удовлетворяющие условию Липшица, поэтому следует дать следующее определение:
Def
1.Функция
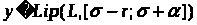 называется решением системы (1), (2) на
отрезке
называется решением системы (1), (2) на
отрезке
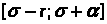 , если она удовлетворяет следующим
условиям:
, если она удовлетворяет следующим
условиям:
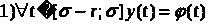
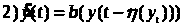 на отрезке
на отрезке
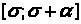 .
.
Естественно возникает вопрос о существовании и единственности такого решения.
Для начала сделаем некоторые обозначения.
a)
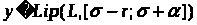
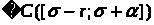 есть функция, определенная на отрезке
есть функция, определенная на отрезке
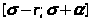 и удовлетворяющая условию Липшица с
константой L,
то есть
и удовлетворяющая условию Липшица с
константой L,
то есть
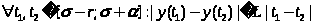 ;
;
b)
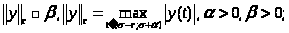
c)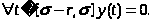
Def
2.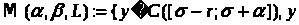 удовлетворяет условиям a),b),c)}
удовлетворяет условиям a),b),c)}
2. Полезная лемма
Lemma
1:
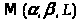 -выпуклое,
замкнутое, ограниченное множество в
пространстве непрерывных на отрезке
-выпуклое,
замкнутое, ограниченное множество в
пространстве непрерывных на отрезке
 функций.
функций.
Proof:
1)Выпуклость:
a)Выберем
произвольные функции
 ,
тогда
,
тогда
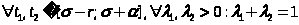
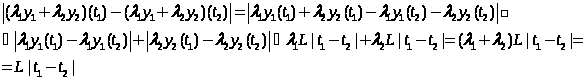
b)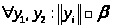
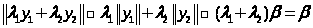 ;
;
c)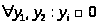 на
отрезке
на
отрезке
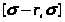
 на
том же отрезке для любых
на
том же отрезке для любых
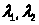 .
.
2)Ограниченность:
Множество
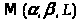 определено так, что все элементы этого
множества лежат в шаре радиуса
определено так, что все элементы этого
множества лежат в шаре радиуса
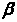
3)Замкнутость:
Возьмем последовательность функций такую, что
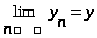 ,
,
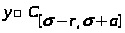 .
.
a)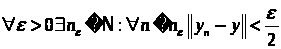
Возьмем
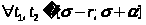 тогда
тогда
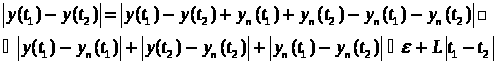
Так как это верно при любом
 ,
то получаем, что предельная функция
удовлетворяет условию Липшица с
константой L.
,
то получаем, что предельная функция
удовлетворяет условию Липшица с
константой L.
b) По
теореме Кантора
 равномерно на отрезке.
равномерно на отрезке.
Предположим, что при этом
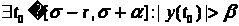 (для
простоты доказательства предположим
что
(для
простоты доказательства предположим
что
 ,
если
,
если
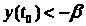 ,
рассуждения проводятся аналогично)
,
рассуждения проводятся аналогично)
Возьмем
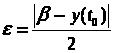 ,
тогда, так как для любого положительного
,
тогда, так как для любого положительного
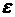 и любого
и любого
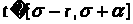 выполнено
выполнено
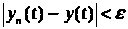 ,
то выполнено и для данных
,
то выполнено и для данных
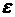 и t.
Получим:
и t.
Получим:
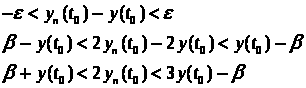
Так как по предположению
 ,
то получаем что
,
то получаем что
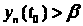 ,
а это невозможно, так как
,
а это невозможно, так как
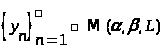 .
Противоречие показывает, что предельная
функция ограничена по норме той же
константой
.
Противоречие показывает, что предельная
функция ограничена по норме той же
константой
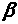 .
.
c)

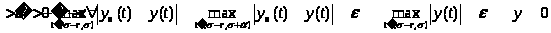
на отрезке
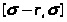 .
.
Видим, что выполнение условий
a,b,c
равнозначно тому что
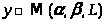 ,
то есть множество
,
то есть множество
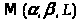 замкнуто.
замкнуто.
Лемма доказана полностью.
3. Существование и единственность решения
Для доказательства теоремы о существовании и единственности липшицевого решения нам потребуется некоторые понятия и важные теоремы, доказательства которых можно, например, найти в книге Кадеца [3].
Def 2. Оператор Т называется вполне непрерывным (компактным), если Т непрерывен и Т отображает любое ограниченное множество в предкомпактное.
Def
3. Семейство Ф
функций φ, определенных
на
 называется равномерно ограниченным,
если
называется равномерно ограниченным,
если
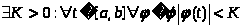
Def
4.Семейство Ф
функций φ, определенных на
 ,
называется равностепенно непрерывным,
если
,
называется равностепенно непрерывным,
если
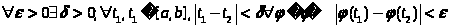
Теорема 1.(Арцела)
Для того чтобы семейство Ф
непрерывных, определенных на отрезке
 функций было предкомпактом в
функций было предкомпактом в
 ,
необходимо и достаточно, чтобы это
семейство было равномерно ограниченным
и равностепенно непрерывным.
,
необходимо и достаточно, чтобы это
семейство было равномерно ограниченным
и равностепенно непрерывным.
Теорема 2.(Шаудера, принцип неподвижной точки)
Если U-замкнутое
ограниченное выпуклое подмножество
пространства Банаха X
оператор
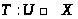 вполне непрерывен, то Т имеет в U
по крайней мере одну неподвижную точку.
вполне непрерывен, то Т имеет в U
по крайней мере одну неподвижную точку.
Именно на теореме Шаудера основано доказательство теоремы о существовании и единственности решения.
Теорема 3.(существование и единственность решения системы (1).(2))
Пусть система (1),(2) такая что:
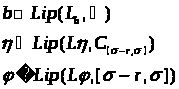
Тогда
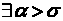 такая что на отрезке
такая что на отрезке
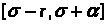 существует решение системы (1),(2),
удовлетворяющее условию Липшица, и оно
единственно.
существует решение системы (1),(2),
удовлетворяющее условию Липшица, и оно
единственно.
Замечание. Для
простоты возьмем
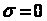 ,
для других значений теорема доказывается
аналогично, или сводится к этому случаю
заменой переменных.
,
для других значений теорема доказывается
аналогично, или сводится к этому случаю
заменой переменных.
Доказательство: Проинтегрировав уравнение (1), увидим, что решение должно удовлетворять условию:
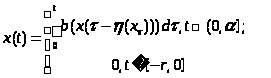
Обозначим
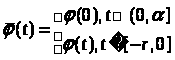
и будем искать решение в виде
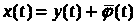
Где
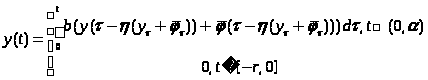
Определим оператор
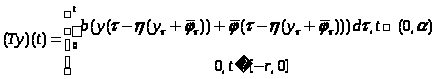 ,
,
Который действует из
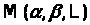 в себя, действительно, возьмем произвольный
элемент
в себя, действительно, возьмем произвольный
элемент
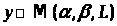
Проверим, удовлетворяет ли образ условию Липшица: возьмем
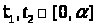
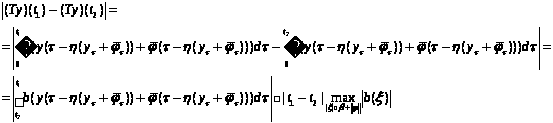
При

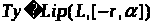
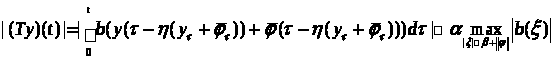
При
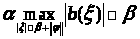 выполнено
выполнено
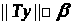 .
.
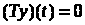 при
при
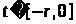 по определению оператора.
по определению оператора.
Выполнение условий a,b,c
означает что
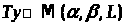 .
.
Для этого необходимо подобрать
параметры
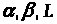 так, чтоб одновременно выполнялись
условия:
так, чтоб одновременно выполнялись
условия:
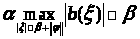 (3)
(3)
 (4)
(4)
Покажем, что оператор Т осуществляет непрерывное отображение:
Возьмем последовательность
 такую что
такую что
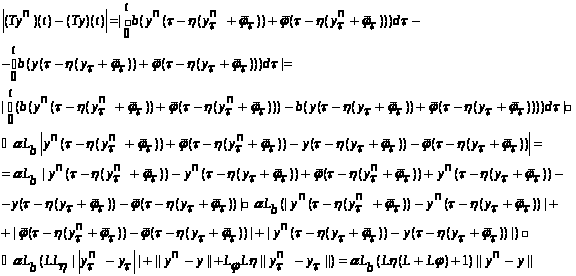
Оценка выполнена на всем интервале,
величина
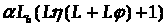 положительна и конечна, отсюда следует,
что при |
положительна и конечна, отсюда следует,
что при |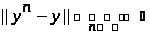
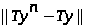 также стремится к нулю, а значит
оператор Т
переводит сходящиеся последовательности
в сходящиеся, а значит он непрерывен.
также стремится к нулю, а значит
оператор Т
переводит сходящиеся последовательности
в сходящиеся, а значит он непрерывен.
Компактность оператора будем
доказывать по теореме Арцела, так как
образ оператора лежит в пространстве
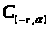 с соответствующей нормой.
с соответствующей нормой.
1)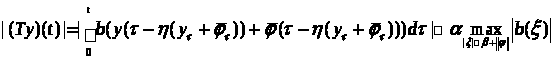 ,
,
правая часть не зависит ни от t, ни от y, значит образ оператора – равномерно ограниченное семейство функций.
2)
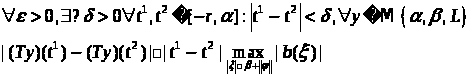
Выбирая
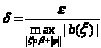 получаем что образ оператора есть
равностепенно непрерывное семейство
функций.
получаем что образ оператора есть
равностепенно непрерывное семейство
функций.
А значит, образ множества
 предкомпакт, а оператор Т
вполне непрерывен.
предкомпакт, а оператор Т
вполне непрерывен.
Так как множество
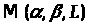 ограничено, выпукло и замкнуто, а оператор
Т компактен
и действует из этого множества в себя,
то по теореме Шаудера существует по
крайней мере одна неподвижная точка
ограничено, выпукло и замкнуто, а оператор
Т компактен
и действует из этого множества в себя,
то по теореме Шаудера существует по
крайней мере одна неподвижная точка
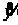 из этого множества.
из этого множества.
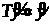 ,
а это значит, что
,
а это значит, что
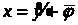 - решение системы (1),(2).
- решение системы (1),(2).
Единственность:
Предположим, что при выполнении
условий теоремы x
и y
– решения системы (1),(2) на интервале
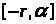 .
.
При
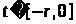 оба решении совпадают с начальными
данными, а значит равны между собой. На
интервале
оба решении совпадают с начальными
данными, а значит равны между собой. На
интервале
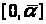 оценим модуль разности функций,
являющимися решениями.
оценим модуль разности функций,
являющимися решениями.
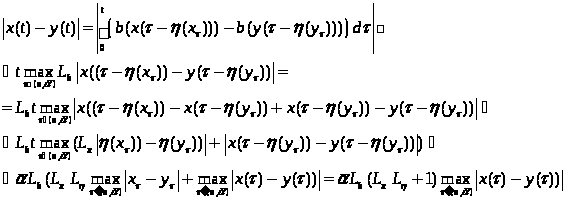
Эта оценка верна для произвольного t отсюда немедленно следует, что
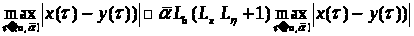 ,
,
Выбирая
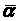 таким малым, чтоб
таким малым, чтоб
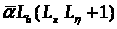 было меньше 1, получаем что
было меньше 1, получаем что
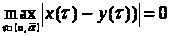 ,
а значит на
,
а значит на
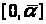
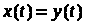 .
Последовательно строя интервалы длинной
.
Последовательно строя интервалы длинной
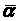 закончим доказательство теоремы.
закончим доказательство теоремы.
4.Пример неединственности (Winston)
Для уравнения
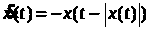 с начальными данными
с начальными данными
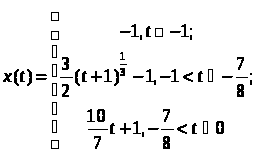
для малых положительных t существует два различных решения:
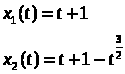
Действительно, проверим, удовлетворяют ли эти функции уравнению:

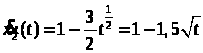
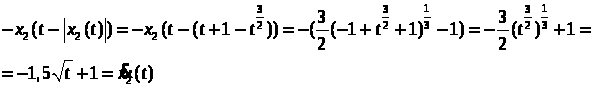
Значит, система имеет два различных
решения. Это происходит потому что при
малых t
аргумент
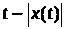 оказывается в окрестности -1, а при этих
значениях начальные данные недостаточно
гладки, не выполнено условие Липшица.
оказывается в окрестности -1, а при этих
значениях начальные данные недостаточно
гладки, не выполнено условие Липшица.
Список использованной литературы
[1] HALE J. K. Theory of functional differential equations. –Berlin; Heidelberg; New York: Springer, 1977.
[2] Резуненко А.В. Краткое введение в обыкновенные дифференциальные уравнения с запаздывающим аргументом. Харьков-2004.
[3] Кадец В.М. Курс функционального анализа. Харьков-2006.
[4] I.D.Chueshov. Introduction to the Theory of Infinite-Dimensional Dissipative Systems . «Аста»-2002.
[5] Д. Хенри. Геометрическая теория полулинейных параболических уравнений. Москва. «Мир»-1985.
[6] Колмогоров А.Н. Фомин С.В. Элементы теории функций и функционального анализа 1976