Визначення та обчислення довжини дуги плоскої кривої в декартових та полярних координатах. Площа поверхні
Наукова робота на тему:
Визначення та обчислення довжини дуги плоскої кривої в декартових та полярних координатах. Площа поверхні
План
Довжина дуги кривої в декартових і полярних координатах
Площа поверхні
Площа поверхні обертання
Площа циліндричної поверхні
Довжина дуги
Це питання для кривої,
заданої рівнянням
 ,
вже розглядалося в раніш.
Там була знайдена формула
,
вже розглядалося в раніш.
Там була знайдена формула
> >
(10.9)
>
(10.9)
Якщо крива задана параметрично, тобто у вигляді
> >
то
>
то
> >
(10.10)
>
(10.10)
Для просторової кривої, що задана параметрично
> >,
>,
довжина дуги обчислюється за формулою
> >
(10.11)
>
(10.11)
аналогічно формулі (10.10). Виведення цієї формули базується на розгляді елемента дуги, кінці якої збігаються з кінцями діагоналі паралелепіпеда, а саме, діагональ є хордою елемента дуги.
У випадку задання кривої в полярній системі координат
> >
,
>
,
Матимемо
> >
(10.12)
>
(10.12)
Пропонується вивести цю формулу, узявши до уваги, що рівняння кривої в полярних координатах можна записати як параметричні з параметром q :
> >
>
>
>
 >
>
і використавши формулу (10.10).
Приклад 1. Обчислити довжину кривої, заданої рівнянням
Розв‘язок. Досить обчислити довжину дуги, що обмежує зверху заштриховану на рис.10.7 фігуру, а потім помножити її на 8. Користуючись формулою (10.12), одержимо
> >
>
Площа поверхні
Площа поверхні обертання
Довжина дуги, що обмежує смужку зверху (рис.10.9),
> >
>
Ця дуга в разі обертання утворить поверхню обертання, Тоді площа поверхні цього конуса нескінченно малої висоти
Нескінченно малою вищого порядку нехтуємо і в результаті одержимо
> >
>
Звідки
> >
(10.7)
>
(10.7)
Площа циліндричної поверхні
На рис. 10.10 зображено циліндричну поверхню з твірними, паралельними осі. Нехай ця поверхня задана рівняннями
> >
>

Рис.10.9 Рис.10.10
Виділивши смужку так, як показано на рис. 10.10 , знайдемо її площу
> >
>
>
 >
(10.8)
>
(10.8)
Зауваження 1. При одержанні формул (10.1) – (10.2), (10.4) – (10.8) виділені елементи фігур вважалися прямокутниками (див. рис. 10.1, 10.4,10.5), сектором з центральним кутом (рис. 10.2), тонким циліндричним шаром (рис. 10.3), що не вплинуло на остаточний результат, бо такі заміни реальних фігур здійснюються нехтуванням нескінченно малих величин вищих порядків. Цей факт можна було б строго довести.
Приклад.
Еліпс із великою піввіссю >
 >
і малою піввіссю >
>
і малою піввіссю >
 >
робить один оберт навколо великої осі
і вдруге – навколо малої осі. Визначити
поверхню обертання еліпса в кожному з
двох випадків.
>
робить один оберт навколо великої осі
і вдруге – навколо малої осі. Визначити
поверхню обертання еліпса в кожному з
двох випадків.
Розв‘язок. Досить розглянути лише половину еліпса:
> >
>
В результаті обертання навколо великої осі одержимо за (11.7)
> >
>
> >
>
де - ексцентриситет еліпса.
За допомогою підстановки
>
 >матимемо
>матимемо
> >
>
У випадку обертання навколо малої осі для обчислення поверхні обертання одержуємо інтеграл
>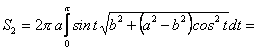 >
>
>
 >
>
В обох випадках поверхня еліпсоїда виразилась через елементарні функції.