Елементи комбінаторики. Початки теорії ймовірностей
ЕЛЕМЕНТИ КОМБІНАТОРИКИ
§ 1. Основні принципи комбінаторики
Досить поширеними є задачі, в яких треба знайти або число можливих розміщень предметів, або число способів, якими можна здійснити деякий вибір, тощо. Такі задачі називають комбінаторними, а галузь математики, яка вивчає теорію скінченних множин, комбінаторикою. Найпростіші задачі комбінаторики вимагають підрахунку числа підмножин заданої множини. Основними принципами (правилами) комбінаторики є принцип суми і принцип добутку.
Принцип суми. Якщо множина A містить п елементів, а множина В - т елементів і А ∩ В = Ø, то множина A U В містить п + т елементів.
Справді, елементи множини А занумеруємо від 1 до п. Серед них немає елементів з множини В, оскільки А ∩ В = 0. Отже, коли ми переходимо до підрахунку елементів, що належать множині В, то починаємо з номера п +1. Далі буде номер п + 2, п + 3 , ..., п + т, оскільки в множині В за умовою т елементів. Цим усі елементи множини A U В буде вичерпано, вони дістануть номери від 1 до п + т.
Правило суми можна сформулювати ще й так: якщо якийсь вибір А можна здійснити п способами, а другий вибір В можна здійснити т способами, то вибір А або В можна здійснити п + т способами.
Принцип суми за індукцією поширюється на к множин.
Принцип добутку. Нехай маємо дві множини:
А={a>1>, а>2>, ..., a>n>}, В={b>1> b>2>, ..., b>n>}.
Тоді множина всіх можливих пар
С={(а>i>, b>i>)ا i=1, 2, ..., п; j = 1, 2, ..., m} містить п-т елементів.
Розіб'ємо множину С на множини
С={(а>1>, b>1>), (а>1>, b>2>), …, (а>1>, b>m>) }
С={(а>2>, b>1>), (а>2>, b>2>), …, (а>2>, b>m>) }
…………………………………
С={(а>n>, b>1>), (а>n>, b>2>), …, (а>n>, b>m>) }
Неважко помітити, що множини С>1>, С>2>, ..., С>n>, попарно не перетинаються і C = C>l> UC>2> U … UC>n>. Оскільки кожна з підмножин С>1>, С>2>, ..., С>n>, містить т елементів, то за принципом суми число елементів в об'єднанні їх дорівнює п • т.
Правило добутку можна сформулювати ще й так: якщо якийсь вибір А можна здійснити п різними способами, а для кожного з цих способів деякий другий вибір В можна здійснити т способами, то вибір А і В у вказаному порядку можна здійснити п • т способами.
Приклад 1. З міста А у місто Б веде 6 шляхів, а з міста Б у місто В 4 шляхи (рис. 298). Скількома шляхами можна проїхати з містам у місто В1 Вибравши один із шести шляхів з міста А у місто Б, далі можемо вибрати шлях від Б до В чотирма способами. Тому на підставі правила добутку дістанемо 6 • 4 = 24.


Приклад 2. До міста А, Б і В додамо ще одне місто Г і кілька нових шляхів (рис. 299). Скількома маршрутами тепер можна дістатися з міста А у місто В?
Розглянемо два випадки: шлях проходить через місто Б або через місто Г. Для кожного з цих випадків за правилом добутку неважко під-| рахувати кількість маршрутів (для першого - 24, для другого - 6). За правилом суми маємо остаточно: 24 + 6 = 30. Отже, загальна кількість маршрутів 30.
Приклад 3. У крамниці продають 5 склянок, 3 блюдця і 4 ложки. Скількома способами можна купити два предмети з різними назвами?
Можливими є три випадки: перший - купують склянку з блюдцем, другий - склянку з ложкою, третій - блюдце і ложку. У кожному з цих випадків за правилом добутку неважко підрахувати кількість можливих варіантів: 15, 20 і 12. За правилом суми маємо остаточно: 15 + 20 + 12 = 47.
Сформулюємо тепер принцип (правило) добутку у загальному вигляді.
Нехай треба виконати одну за одною k дій. Якщо першу дію можна виконати n, способами, другу - п>2> способами,..., k-ту- п>k>> >способами, то всі k дій разом можуть бути виконані n способами, де п = п>2>•п>2> • ... • п>k>.
§ 2. Перестановки
Нехай треба підрахувати число способів, за якими можна розмістити в ряд n предметів. Якщо дані предмети розглядати як елементи множини то кожне розміщення є скінченною множиною, елементи якої записано у певному порядку.
Скінченні множини, для яких істотним є порядок елементів, називаються впорядкованими. Вказати порядок розміщення елементів у скінченній множині з п елементів означає поставити у відповідність кожному елементу даної множини певне натуральне число від 1 до п .
Дві впорядковані множини називаються рівними, якщо вони складаються з тих самих елементів і однаково впорядковані. З цього випливає, що множини (а, b, с) і (b, с, а) - це різні впорядковані множини.
Означення. Будь-яка впорядкована множина, що складається з п елементів, називається перестановкою з п елементів.
Перестановки з п елементів складаються з одних і тих самих елементів, а відрізняються одна від одної лише порядком.
Наприклад, з елементів множини А = {1, 2, 3} можна утворити шість перестановок: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1).
Число перестановок у множині з п елементів позначають Р>п> .
Доведемо, що
Р>п>=n!, (1)
де п! = 1•2• ... •п .
Для доведення застосуємо метод математичної індукції.
1. Якщо п = 1, маємо Р>п> =1 = 1!; тобто формула (1) виконується.
2. Припустимо, що для n = 1 рівність Р>к> = k! виконується (п і k - натуральні числа).
Доведемо, що для п = k +1 виконуватиметься рівність
Р>k>>+1>=(к + 1)!
На перше місце можемо поставити будь-який з k + 1 елементів множини. Тоді k місць, які залишилися, можна задавати будь-якою перестановкою з k елементів. Число таких перестановок Р>k> . Таким чином, перестановку з k + 1 елемента даної множини можна розглядати як пару: на першому місці - елемент множини, на другому - перестановка з k елементів, що залишились (таких перестановок Р>k>). На підставі принципу добутку число всіх перестановок (всіх таких пар)
Р>k>>+1>=(к + 1) Р>k> , (1)
З формули (2) дістаємо
Р>k>>+1>=(к + 1) Р>k> = Р>k> • (к + 1) =k! • (k+1)=1•2•…•k• (k+1)=(k+1)!
Приклад 1. Скількома способами можна розмістити в один ряд червону, синю, чорну та зелену фішки?
Р>4> = 4! = 1•2•3•4 = 24.
Приклад 2. Скількома способами можна розмістити за столом 10 чоловік?
Р>10>=10! = 1•2•3•4•5•6•7•8•9•10 = 3628800.
§ 3. Розміщення
Нехай деяка множина складається з п різних елементів.
Означення. Розміщеннями з п елементів по k називаються підмножини, що мають k елементів, вибраних з даних п елементів і розміщених у певному порядку (k<п).
Розміщення можуть відрізнятися одне від одного або самими елементами, або порядком їх розміщення.
Наприклад, нехай маємо три елементи: 1, 2, 3. Тоді розміщення з трьох елементів по два мають вигляд: (1, 2), (1, 3), (2, 1), (3, 1), (2, 3), (З, 2). Розміщення (1, 2) і (2, 1) відрізняються лише порядком. Вони утворюють два різних числа 12 та 21. Розміщення (1, 2) і (1, 3) відрізняються самими елементами. Вони утворюють два різних числа 12 і 13.
Кількість розміщень з даних п елементів по k позначають через Аk>n>, = k < п.
Доведемо, що
Аk>n> = n(n-1)(n-2)...(n-(k-1)). (1)
Якщо множина містить п елементів, то при утворенні розміщень по одному елементу таких розміщень буде п (стільки, скільки елементів у множині). Отже, Аk>n> = п.
Утворимо тепер розміщення з п елементів по два. Для цього візьмемо п розміщень по одному елементу і до кожного розміщення допишемо кожний з решти п -1 елементів даної множини. Таким чином, Аk>n> = n(n-1).
Застосуємо метод математичної індукції. Припустимо, що для А2>n> правильною є формула (1). Розміщення з п елементів по k + і можна розглядати як пару: на першому місці будь-яке розміщення з п елементів по k (їх кількість Аk>n> ), на другому - будь-який елемент з решти п - k елементів. За правилом добутку дістанемо
А> >>n> k +1= А> >>n> k (n-k). (2)
Користуючись формулою (1), маємо
А> >>n> k +1=п(п-1)(п-2)...(п-(k-і))(п-k) = = n(n - 1)(n - 2)...(n- (k -1))(n-(k +1-1)).
Оскільки

то формулу (1) можна записати ще так:
 .
(3)
.
(3)
Приклад 1. Скількома способами можна вибрати з 10 кандидатів три особи на три різні посади?
Для розв'язування задачі треба знайти число розміщень з 10 елементів по три. Отже, за формулою (1) маємо
A3>10> =10•9•8 = 720.
Приклад 2. Скільки трицифрових чисел з різними цифрами можна утворити з цифр 0, 1, 2, 3, 4?
Загальна кількість трицифрових чисел з різними цифрами є кількістю
розміщень з 5 елементів по три, тобто А3>5> = 5 • 4 • 3 = 60. Проте із загальної кількості чисел треба відкинути числа, що починаються з нуля. Таких чисел стільки, скільки можна утворити розміщень з чотирьох цифр по два без нуля, тобто А2>4> =4•3 = 12. Отже, шукана кількість трицифрових чисел дорівнює 60 - 12 = 48 .
§ 4. Комбінації
Означення. Будь-яка підмножина з k елементів даної множини, яка містіть п елементів, називається комбінацією з п елементів по k.
З одного елемента можна утворити тільки одну комбінацію. З двох елементів а і b можна утворити дві комбінації по одному елементу і тільки одну комбінацію з двох елементів.
З трьох елементів a, b, c можна утворити такі комбінації:
{a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}.
Комбінації з п елементів даної множини по k можна також розглядати як розміщення з п елементів по k, які відрізняються принаймні одним елементом. Виникає запитання, як визначити кількість комбінацій з n елементів по k. Число комбінацій з п по k позначається Сk>n> . Доведемо, що
 .
(1)
.
(1)
Розглянемо множину, яка складається з п елементів, і комбінації, які складаються з k елементів. Всього комбінацій Сk>n>. Якщо з кожної такої комбінації утворити всі можливі перестановки (їх буде Р>k> = k!), то дістанемо всі можливі розміщення з п елементів по к, тобто число Аk>n>. Отже,
Аk>n>> >= Р>k> •Сk>n> , (2)
звідки

Зауважимо, що за означенням покладають 0! = 1. Тому неважко помітити, що С1>1>=1 і Сn>n> = 1.
Приклад. Збори з 30 осіб вибирають трьох делегатів на конференцію. Скількома способами це можна зробити?
Із множини у 30 осіб
треба вибрати підмножину з трьох осіб.
Це можна
зробити
 способами .
способами .
§ 5. Властивості комбінацій

Числа





 і т.д. зручно записати у вигляді такої
трикутної таблиці:
і т.д. зручно записати у вигляді такої
трикутної таблиці:

Обчисливши значення кожного символу, дістанемо

Таку таблицю називають
трикутником
Паскаля. На
«бічних сторонах» цього трикутника
стоять одиниці, а "всередині", за
властивістю 2, кожне число дорівнює сумі
двох чисел, що стоять над ним: 2=1+1; 3=1+2;
4=1+3; 6=3+3 і т.д. Ця властивість дає можливість
виписувати послідовно рядки трикутника
Паскаля, не обчислюючи перед цим значення
символів
 .
.
§ 6. Біном Ньютона
З алгебри відомо формули скороченого множення:
(a + b)2 =a2 +2ab + b2,
(а + b)3= а3 + 3a2b + 3ab2 + b2.
Коефіцієнти в правих частинах цих формул збігаються відповідно з другим і третім рядками трикутника Паскаля. Чи буде зберігатись ця закономірність для 4-го, 5-го і т.д. степеня суми?
Щоб відповісти на це запитання, розглянемо вираз (1 + х)п , де п -натуральне число. Запишемо цей вираз як добуток співмножників:

Розкривши у правій частині дужки, дістанемо многочлен, який можна розмістити за степенями букви х. До цього многочлена ввійдуть усі степені х з показниками від 0 (вільний член) до п. Щоб записати цей многочлен, треба знайти його коефіцієнти. Нехай ціле число k задовольняє нерівності 0 < k < n. З'ясуємо, який коефіцієнт має степінь хк. Цей коефіцієнт дорівнює кількості подібних членів виду хk, які дістанемо, розкривши дужки. Щоб дістати хk, беремо в k дужках другий доданок, а в інших п - k дужках перший доданок, і перемножуємо їх. Такий вибір можна здійснити Сk>п> способами. Отже, розкривши дужки, матимемо Сk>п> подібних членів виду хk. Після зведення подібних членів дістанемо відповідний член Сk>п> xk. Залишається надати k всіх можливих значень k = 0, 1, 2, ..., п, і члени додати. Таким чином, можна записати:

або, використовуючи символ суми,

Нарешті, розглянемо вираз (а + b)п . Подамо його у вигляді

Якщо позначити
 = х,
то за формулою (2) дістанемо
= х,
то за формулою (2) дістанемо

або

Формула (3) називається формулою бінома Ньютона.
Розгорнутий вигляд формули (3):

З формули (4) видно, що її коефіцієнти - це рядки трикутника Паскаля.
Поклавши у формулі (4) а = b = 1, дістанемо

Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}.
ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ
§ 1. Про предмет теорії ймовірностей
До цього часу розглядалися задачі, в яких результат дії був однозначно визначеним. Проте в житті, у тому числі й в економічній діяльності, виникає потреба розглядати задачі, в яких результат дії не визначається однозначно. Якщо, наприклад, підкинути один раз кубик, не можна передбачити, як саме він упаде. Проте при багаторазовому підкиданні може встановитися певна закономірність. Те саме стосується і процесу обробки якої-небудь деталі. Розміри різних деталей будуть відхилятися від деякої певної величини. Ці відхилення мають випадковий характер, адже розміри щойно виготовленої деталі не дають змоги точно визначити розміри наступної деталі. Проте якщо розглядати партії з великої кількості деталей, то середнє арифметичне розмірів виготовлених деталей у різних партіях є приблизно однаковим.
Подібного роду закономірності і вивчає теорія ймовірностей.
Принципових змін зазнає і сама постановка задачі. Нас вже цікавить не результат конкретного досліду, а те, що саме дістаємо після багаторазового повторення цього досліду.
Теорія ймовірностей вивчає закономірності масових випадкових подій. Вона є основою для вивчення статистичних даних, своєрідним містком між математичним і статистичним аналізами. Нарешті, теорія ймовірностей знаходить широке застосування у задачах економічного характеру. Наведемо приклади.
1. Скільки треба прокласти телефонних ліній до обласного (районного) центру при організації телефонного зв'язку в області (районі)?
Це чисто імовірнісна задача. Адже завчасно не можна передбачити, скільки викликів і в який проміжок часу надійде до центру. Якщо телефонних ліній прокласти замало, то до центру дуже важко буде зателефонувати. Якщо ж їх прокласти забагато, то витрати на організацію телефонного зв'язку будуть надмірними, що є економічно невигідним.
2. Фірма виготовляє телевізори на трьох заводах А, В, С. їй відомо, який процент продукції на кожному заводі становить брак. Фірма хоче визначити ймовірність того, що бракований телевізор виготовлено, скажімо, на заводі Л.
3. Підприємство, яке виробляє продукти споживання, знає, який процент мешканців міста складають жінки і який - мешканці, чий річний заробіток перевищує 6 тис. грн. Підприємство на розвиток своєї ринкової стратегії хоче знати, який процент мешканців міста складають жінки. чий річний заробіток перевищує 6 тис. грн.
§ 2. Основні поняття теорії ймовірностей
Випробуванням (або дослідом) називається експеримент, який можна проводити в однакових умовах будь-яку кількість разів. Результат випробування називається подією або наслідком.
Наприклад, підкидання монети - випробування, поява на ній "герба" -подія. Виготовлення деталей - випробування, поява бракованої деталі -подія.
Події позначають великими буквами латинського алфавіту А, В, С, ....
Означення 1. Випадковою подією називається подія, яка може відбутися або не відбутися під час здійснення певного випробування.
Наприклад, виграш у суперника при грі у шахи, поява бракованого виробу при серійному їх випуску - випадкові події.
Означення 2. Масовими називаються однорідні події, що спостерігаються за певних умов і можуть бути відтворені необмежену кількість разів.
Масовими вважають і ті події, для яких відповідні випробування не можна відтворити, але є можливість спостерігати аналогічні випробування у великій кількості. Наприклад, виклик телефонної станції, прихід суден далекого плавання в порт призначення.
Подія, яка при кожному випробуванні обов'язково відбувається, називається вірогідною. Наприклад, якщо в урні лише білі кулі, то при кожному випробуванні обов'язково вийматиметься тільки біла куля.
Подія, що не може відбутися при жодному випробуванні, називається неможливою. Наприклад, поява чорної кулі, якщо в урні лише білі, є неможливою подією.
Означення 3. Сукупність подій утворює повну групу подій, якщо внаслідок випробування хоч одна з цих подій напевно відбудеться (наприклад, поява 1, 2, 3, 4, 5, 6 очок під час кидання грального кубика).
Якщо повна група складається з двох подій, то такі події називаються протилежними і позначаються А і Ặ.
Означення 4. Події А>1 >, А>2 >, ... , А>п> називаються попарно несумісними у даному випробуванні, якщо ніякі дві з них не можуть відбутися разом.
Поява 1, 2, 3, 4, 5, 6 очок під час одного кидання грального кубика - приклад множини з шести несумісних подій.
Події А>1>, А>2>, ... , А>п> можуть бути рівноможливими. Під рівноможливими розуміють такі події, кожна з яких не має ніяких переваг у появі частіше за іншу під час багаторазових випробувань, що проводяться за однакових умов.
Найважливішим поняттям теорії ймовірностей як галузі математики є поняття ймовірності випадкової події.
Ймовірність - числова характеристика появи випадкової події за певної умови, яка може бути відтворена необмежену кількість разів. Розглянемо поняття ймовірності грунтовніше.
§ 3. Класична ймовірність
Нехай маємо 100 деталей, з яких 97 стандартних і 3 браковані. Дослід полягає в тому, що навмання беруть одну деталь. Не можна наперед сказати, якою буде взята деталь - стандартною чи бракованою. Оскільки ми можемо вибирати лише одну яку-небудь деталь, то поява стандартної чи бракованої деталі - випадкові події, які утворюють повну групу з 100 несумісних і рівноможливих подій. З цих 100 випробувань появі стандартної деталі сприяють 97 наслідків, а появі бракованої- 3 наслідки. Нехай А -подія, яка полягає у виборі стандартної деталі, а В - бракованої. Тоді числа 97/100 і 3/100 характеризують можливість здійснення відповідно події А чи В. Ці числа називають ймовірностями подій А і В і позначають

Означення. Ймовірністю випадкової події називають відношення кількості наслідків випробувань, які сприяють появі цієї події, до загальної кількості всіх рівноможливих несумісних наслідків, які утворюють повну групу подій.
Позначають
 (1)
(1)
де п - загальна кількість всіх рівноможливих результатів експерименту;
т - кількість результатів експерименту, сприятливих для події А.
Розглянуте означення ймовірності називають класичним. Із класичного означення ймовірності випливають такі властивості:
1. Ймовірність кожної
події А є
невід'ємним числом, що не перевищує
одиниці. Справді, число т
випробувань,
сприятливих для події А,
справджує
нерівності 0 < т
< п , звідки
 тобто
тобто

2. Ймовірність неможливої події V дорівнює нулю: P(V) = 0 . Дійсно,
за формулою (1)

Приклад 1. У коробці міститься шість однакових занумерованих куль. Довільно по одній виймають усі кулі. Знайти ймовірність того, що номери вийнятих куль зростатимуть.
Позначимо через А подію, ймовірність якої треба знайти. Наслідками випробувань є перестановки з шести елементів. Отже, число всіх можливих випадків п = Р>6> =6! = 720. Для події А сприятливим є лише один наслідок випробування, тобто т = 1. Тому

Приклад 2. Набираючи номер телефону, абонент забув останні три цифри і, пам'ятаючи що всі вони різні, набрав їх навмання. Знайти ймовірність того, що набрано потрібний номер телефону.
Нехай А - подія, ймовірність якої треба знайти. У цьому випадку п = А3>10>, т = 1. Тоді

Приклад 3. Партія з 10 деталей має 7 стандартних. Знайти ймовірність того, що серед вибраних навмання шести деталей чотири стандартні.
Нехай А - подія, ймовірність якої треби знайти. У цьому випадку п = C6>10>. Щоб знайти число наслідків випробувань, в яких чотири стандартні деталі, діємо так: вибираємо ці 4 деталі із загальної їх кількості. Це можна зробити С>7>4 способами. Решту 6-4 = 2 нестандартних деталей можна вибрати С>3>2 способами. За правилом добутку число наслідків випробувань, що сприяють появі події А, буде т = С>7>4 · С>3>2 . Шукана ймовірність дорівнює

§ 4. Статистична ймовірність
Нехай виконуються випробування, які можна повторити будь-яку кількість разів, і нехай при багаторазовому повторенні випробування події, які відбулися в попередніх випробуваннях, ніяк не впливають на події, що відбудуться у даному випробуванні.
Якщо проведено п
однакових
випробувань і
· т - число
випробувань, в яких відбулася подія А,
то відношення
 називають відносною
частотою події
А у проведеній
серії випробувань. Таким чином, відносна
частота події А
визначається
формулою
називають відносною
частотою події
А у проведеній
серії випробувань. Таким чином, відносна
частота події А
визначається
формулою

Теорія ймовірностей розглядає лише такі події, для яких характерна властивість стійкості відносних частот. Ця властивість полягає в тому, що відносна частота події А при великій кількості випробувань мало відрізняється від деякого числа.
Нехай маємо таблицю, де наведено результати дослідів, пов'язаних із підкиданням симетричної монети:
Число підкидань 4040 2048 0,5069
Число появ "герба" 12000 6019 0,5016
Відносна частота 24000 12012 0,5005
Тут відносні частоти відхиляються від числа 0,5 тим менше, чим більша кількість випробувань. Проте число 0,5 є класичною ймовірністю випадання "герба" при одному підкиданні симетричної монети.
Як бачимо, означення класичної ймовірності не вимагає, щоб випробування насправді виконувались: означення відносної частоти вимагає, щоб випробування були фактично виконані. Іншими словами, класичну ймовірність обчислюють до досліду, а відносну частоту - після досліду.
Проте класична ймовірність має обмежене застосування, оскільки далеко не завжди в реальних умовах можна виділити рівноможливі випадки у скінченній кількості.
Якщо підкидати несиметричну монету (із зміщенням від геометричного центра ваги), то відносні частоти появи "герба" так само мають властивість групуватися навколо певного числа р при збільшенні кількості випробувань. Проте число р нам невідоме, бо монета не є симетричною і для кожної монети воно буде своїм.
Прийнято вважати це невідоме число р статистичною ймовірністю появи "герба" при підкиданні несиметричної монети.
Означення. Ймовірністю події А називається невідоме число р, навколо якого зосереджується значення відносної частоти події А при зростанні числа випробувань.
Щойно наведене означення ймовірності називають статистичним. Отже,
Р>п>(А)≈Р(А) = р, (2)
де Р(А) - ймовірність події А; Р>п>(А) - відносна частота; п -кількість випробувань.
Наближена рівність (2), яка виражає властивість стійкості відносних частот, є однією з найважливіших закономірностей масових випадкових подій.
Приклад. Із 1000 довільно вибраних деталей приблизно 3 браковані. Скільки бракованих деталей приблизно буде серед 2100 деталей?
Позначимо через А подію, коли навмання взята деталь бракована. Тоді відносна частота

Якщо серед 2100 деталей виявиться х бракованих, то ймовірність події А

Оскільки Р>п>
(А) ≈ Р(А),
то
 ,
звідки х =
6.
,
звідки х =
6.
§ 5. Зв'язок теорії ймовірностей з теорією множин
Множину всіх можливих наслідків випробування називають основним простором або простором елементарних подій (наслідків) і позначають Q. Наслідок позначають со.
Випадковою подією (наслідком) називається будь-яка підмножинаЛ простору Q, тобто будь-яка множина наслідків. Наслідки, які утворюють подію А, називають сприятливими для А (соє А). Подія А настає тоді і тільки тоді, коли настає елементарна подія (наслідок), сприятлива для А.
Тому теорія ймовірностей і теорія множин мають багато спільного. Втім, в них йдеться про одне й те саме різними словами, що видно з такої таблиці:

Приклад. Підкидають два гральних кубики. Подія А - сума очок, які з'явились, дорівнює 10; подія В - принаймні один раз з'явиться шістка. Опишіть простір елементарних подій та події A U В і А ∩ В.
Простір елементарних подій, або множину можливих наслідків випробування, можна записати як набір усіх можливих впорядкованих пар чисел від 1 до 6 (кожну із шести граней першого кубика можна розглядати у парі з будь-якою гранню другого кубика). Отже,
Ω = {(1; 1), (1; 2),...(1; 6), (2; 1), ..., (6; 5), (6; 6)}.
Всього за правилом добутку маємо 6 • 6 = 36 елементів.
Подію А задаємо переліком елементів, які її складають:
А = {(4; 6), (5; 5), (6; 4)}.
Аналогічно
В={(6; 1), (6; 2), (6; 3), (6; 4), (6; 5), (6; 6), (1; 6), (2; 6), (3; 6), (4; 6), (5; 6)}.
Об'єднання A U В - подія, яка полягає в тому, що відбудеться хоча б одна з подій А або В. Тому A U В означає, що або сума очок на гранях, які випали, дорівнює 10, або принаймні один раз з'явиться шістка.
Оскільки елементи (4; 6) і (6; 4) входять одночасно ідо А, ідо В, то
A U B = ((5; 5)}U B.
Подія А ∩ В складається з двох елементів, які входять і до А, і до В:
A ∩ B = {(4; 6), (6; 4)}.
§ 6. Геометричні ймовірності
Класичне означення ймовірності ґрунтується на тому, що випробування має скінченну кількість наслідків. Проте є досліди, які мають нескінченну кількість наслідків.
Наприклад, нехай на площині міститься область Ω. і в ній міститься інша область А (рис. 300).

Припустимо, що в область Ω навмання кидають точку. Як визначити ймовірність того, що кинута точка потрапить до області А? Природно вважати, що ймовірність попадання точки до області А пропорційна площі цієї області і не залежить від розміщення та форми цієї області.
Підмножини області Ω, які мають площу, називатимемо в такому разі випадковими подіями. Якщо А - випадкова подія, то вважатимемо, що
 (1)
(1)
де S(A) – площа A, S(Ω.) -площа Ω.
Ймовірності, що подаються як відношення площ областей (довжин відрізків, об'ємів тіл), називають ще геометричними ймовірностями.
Приклад 1. Знайти ймовірність того, що навмання взята точка з круга радіуса R належатиме квадрату, вписаному в коло, яке обмежує круг (рис. 301).

За означенням геометричної ймовірності маємо

де S>1> - площа квадрата AВCD; S - площа круга радіуса R.
Оскільки АВ2 = 2R2, то S>1> = 2R2. Тому

На перший погляд здається, що геометричні ймовірності є мало корисними для застосувань. Проте це не так. Багато задач, серед яких і ті, що висуваються практикою, врешті-решт зводяться до відшукання ймовірності попадання точки в деяку область.
Приклад 2 (задача Бюффона). Нехай на площині проведено паралельні прямі так, що відстань між сусідніми прямими дорівнює 2а. На площину навмання кидають голку завдовжки 2l, l<а. Яка ймовірність того, що голка перетне якусь із цих прямих?
Положення голки
однозначно визначається величиною кута
де та відстанню від середини голки до
найближчої прямої (рис. 302). Отже, можна
взяти за простір Ω
елементарних
наслідків прямокутник
 ,
0<у<а. Оскільки
з ΔACBD
= ВС = ABsinx
= lsinx,
то голка перетне
пряму тільки тоді, коли у
< d,
тобто
,
0<у<а. Оскільки
з ΔACBD
= ВС = ABsinx
= lsinx,
то голка перетне
пряму тільки тоді, коли у
< d,
тобто
 (2)
(2)
Точки, координати яких
задовольняють нерівності (2), утворюють
фігуру, заштриховану на рис. 303. Згідно
з рівністю (1) площа цієї фігури, поділена
на площу прямокутника, і буде дорівнювати
шуканій імовірності. Площа прямокутника
 .
Площа
заштрихованої фігури
.
Площа
заштрихованої фігури


Формула (3) є корисною при розв'язуванні багатьох задач. Зокрема, користуючись цією формулою, можна наближено обчислити число п. Справді, з формули (3) маємо
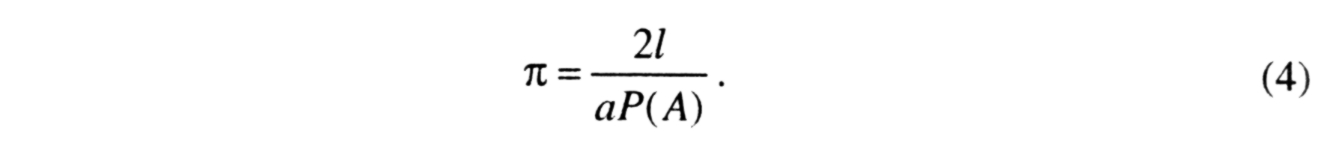
Нехай голку кинуто п
разів і т
разів вона
перетнула пряму. При досить великих п
віднось Тому
при досить великих п
відносна
частота
 як завгодно мало відрізняється від
імовірності Р(А).
Тому
як завгодно мало відрізняється від
імовірності Р(А).
Тому

Під час проведення випробувань голку було кинуто 5000 разів, причому найближчу пряму вона перетнула 2532 рази. Довжина голки була 36 мм, відстань між паралельними прямими 45 мм. Отже,

§ 7. Теорема про додавання ймовірностей несумісних подій
Розглянемо спочатку приклад.
Припустимо, що в урні містяться 5 білих, 3 чорних, 2 червоних і 7 синіх куль. Знайдемо ймовірність того, що з урни вийняли кулю білого або чорного кольору.
Нехай подія А - поява білої кулі, В - поява чорної кулі, С = A U В -поява білої або чорної кулі. Оскільки події С сприяють 8 наслідків, а число усіх куль в урні дорівнює 17, то Р(С) = Р(А U В) = 8/17 .
Цю ж імовірність можна знайти інакше: Р(А) =5/17, Р(В) = 3/17, отже, Р{А) + Р(В) = 8/17. Таким чином, Р(А U B) = Р(А) + Р(В).
Теорема 1. Якщо події А і В несумісні (А ∩ В = 0 ), то
Р(А U В) = Р(А) + Р{В). (1)
Нехай із числа п усіх рівно можливих наслідків m>1> результатів є сприятливими для події А, а т>2> - для події В. Оскільки події А і В несумісні, то поява події А виключає появу події В і навпаки, тому число випробувань, сприятливих для події A U В, дорівнює m>1 >+ т>2>. Звідси на основі класичного означення ймовірності дістаємо

що й треба було довести.
Наслідок 1. Якщо події А>1>, А>2>, ..., А>n> попарно несумісні (тобто A>i> ∩ A>j> = 0 при і ≠ j, i,j = 1, 2, ..., п), то

Формула (2) є узагальненням формули (1).
Наслідок 2. Ймовірність протилежної до А події А дорівнює

Справді, оскільки A U А = Ω, (Ω - простір елементарних подій) і P(Ω) = 1, то за теоремою 1 маємо

звідки і дістаємо (3).
Наслідок 3. Якщо попарно несумісні події А>1>, А>2>, •...• А>n> утворюють повну групу, то сума ймовірностей цих подій дорівнює 1.
Оскільки А>1> U А>2> U • … • U А>n>> >= Ω і P(Ω) = 1, то за формулою (2) маємо
P(А>1>)+P( А>2>) +...+ P(А>n>)=1. (4)
Приклад 1. У лотереї розігруються 1000 білетів, з них на один припадає виграш 5000 грн., на 10 білетів - виграш по 1000 грн, на 50 білетів - виграш 200 грн, на 100 білетів - виграш 50 грн. Решта білетів невиграшні. Знайти ймовірність виграшу на один білет не менш як 200 грн.
Позначимо події: А - виграш не менш як 200 грн, А>1> - виграш 200 грн, А>2> - виграш 1000 грн, A>3> - виграш 5000 грн.
Подія А виражається через об'єднання трьох несумісних подій А>1>, А>2>, А>3>, тобто А = А>1> U А>2> U А>3>. За теоремою 1 дістанемо
P(A)=P(А>1>)+P( А>2>) +.P(А>3>),
або
P(A)= 0,050+ 0,010+ 0,001 = 0,061.
Приклад 2. При прийманні партії підлягає перевірці половина виробів. Умовами приймання передбачається не більше, ніж 2 % бракованих виробів. Визначити ймовірність того, що партію з 100 виробів, яка містить 5 % браку, буде прийнято.
Оскільки 2 % від 50 дорівнює одиниці, то через А позначимо подію, яка полягає в тому, що під час перевірки не отримано жодного бракованого виробу, а через В - лише один бракований виріб. Партію з 100 виробів, яка містить 5 % браку (тобто 5 бракованих виробів), буде прийнято за умови, що має місце або подія А, або подія В. Події А і В є несумісними. Тому за формулою (1) шуканою є ймовірність події C = A U B.
Із 100 виробів 50 можна вибрати C50>100>) способами. Із 95 небракова-них виробів 50 можна вибрати C50>95> способами. Тому

Приклад 3. Для виготовлення деталі придатними є валики з діаметром 11,99 - 12,20 мм. Автомат виготовляє 1 % валиків, діаметр яких менший від 11,99 мм, і 2 % - діаметр яких більший за 12,20 мм. Яка ймовірність того, що навмання взятий з виробленої партії валик буде непридатний для виготовлення деталі?
Нехай А - подія, ймовірність якої треба визначити. Тоді Ặ - подія, яка полягає в тому, що навмання взятий валик придатний.
За формулою (3) знаходимо

§ 8. Теорема додавання ймовірностей довільних подій
Теорема. Якщо А i В - довільні події, то

Якщо події А і В несумісні, то Р(А ∩ В) = Ø, і правильність формули (1) випливає з рівності (1) § 7.

Віднявши від рівності (4) рівність (2), знаходимо
Р(А) + Р(В) = Р(А US)- P(A ∩ В),
звідки і випливає рівність (1).


Приклад 2. У групі 30 учнів. З них 12 вивчають німецьку мову, 15 - англійську, 5 - англійську і німецьку, а решта - інші мови. Яка ймовірність того, що навмання вибраний учень вивчає англійську або німецьку?
Позначимо події: А - навмання вибраний учень вивчає німецьку мову; В - навмання вибраний учень вивчає англійську мову. За умовою n(A) = 12, п(В) = 15. Події А і В є сумісними, оскільки А ∩ В≠Ø і n (А ∩ В) = 5 (рис. 305). Тоді

§ 9. Умовні ймовірності
Часто одна подія А впливає на можливість появи іншої події. В цьому випадку події А і В називають залежними. Нехай, наприклад, з урни, в якій 15 білих і 10 чорних куль, навмання виймають послідовно одну за одною дві кулі. Розглянемо події: А - перша куля біла, В - друга куля біла. Зрозуміло, що Р(А) = 15/25=3/5. Якою буде ймовірність події В?
Якщо подія А відбулася, то серед 24 куль, що залишилися, білих 14 і Р(В) =14/24=7/12; якщо ж подія А не відбулася (перша куля виявилася чорною), то Р{В) =15/24= 5/8.
Отже, ймовірність появи події В залежить від здійснення події А, тобто А і В - залежні події. У такому випадку кажуть, що ймовірність появи події В умовна.
Означення. Нехай А і В - довільні події. Умовною ймовірністю Р(В/А) події В називають ймовірність події B, знайдену в припущенні, що подія А вже відбулася.
Теорема. Якщо A i В- довільні події, причому Р(А) ≠ 0, то
Р(АПВ) = Р(А)-Р(В/А). (1)
Нехай для події А сприятливими є т рівноможливих наслідків випробування із загальної їх кількості п, а для події А ∩ В – k (рис. 306). Тоді

Проте якщо подія А відбулася, можливі лише ті т наслідків випробування, які є сприятливими для події А, причому k з них очевидно є сприятливими для події В. Отже,

З умови Р(А) ≠ 0 випливає, що т = 0.
Другу з рівностей (2), враховуючи першу з них і рівність (3), можна записати у вигляді

що й треба було довести.
Доведену теорему називають теоремою множення ймовірностей для двох подій. Помінявши місцями А і В, дістанемо другий запис цієї теореми:


Приклад. На заводі 96% телевізорів визнаються придатними. У кожній партії з 100 придатних телевізорів у середньому 75 є першого сорту. Знайти ймовірність того, що телевізор, взятий з такої партії, є першого сорту.
Подія А - телевізор є придатним, подія В - телевізор є першого сорту. Шуканою величиною є Р(А ∩ В), оскільки для того, щоб телевізор був першого сорту, треба, щоб він одночасно був і придатним (подія А), і першого сорту (подія В). За умовою Р(A) = 0,96, Р(В/А) = 0,75. Отже,
Р(А ∩В) = Р(А) • Р(В І А) = 0,96 • 0,75 = 0,72.
§ 10. Теорема про множення ймовірностей незалежних подій
Означення 1. Події А і В називаються незалежними, якщо настання однієї з подій не впливає на ймовірність настання другої події.
З цього означення випливає, що незалежні події - це такі дві рівності:
Р(А/В) = Р(А), Р(В/А) = Р(В). (1)
Теорема. Ймовірність одночасної появи двох незалежних подій дорівнює добутку ймовірностей цих подій.
Оскільки Р(А ∩В) = Р(А/В) • Р(В), то, враховуючи рівність (1), дістаємо
Р(А ∩ В) = Р(А) • Р(В). (2)
Навпаки, неважко довести, що виконання рівності (2) означає незалежність подій А і В. Справді, оскільки

то відповідно до означення умовної ймовірності праву частину цього виразу можна замінити на Р(А/В), тобто Р(А) = Р(А/В). Аналогічно дістаємо Р(В) = Р(В /А). Отже, рівність (2) гарантує незалежність подій.
Означення 2. Кілька подій називаються незалежними в сукупності, якщо будь-яка з них не залежить від будь-якої сукупності решти.
Для незалежних у сукупності подій має місце рівність

Формула (3) є узагальненням формули (2) на випадок будь-якої скінченної кількості незалежних у сукупності подій.
На практиці для перевірки незалежності подій рідко використовують означення. Частіше виходять з інтуїтивних міркувань, пов'язаних з характером випробування. Так, при підкиданні двох монет очевидно, що поява якої-небудь сторони на одній з них не впливає на умови підкидання іншої. Тому випадання будь-яких сторін на кожній з них є незалежними подіями.
Приклад 1. Імовірність безвідмовної роботи верстата протягом зміни дорівнює 0,9. Знайти ймовірність безвідмовної роботи двох верстатів протягом зміни.
Подія А - безвідмовна робота протягом зміни першого верстата, В -другого. Припускаючи, що події А і В є незалежними, за формулою (1) знайдемо

Приклад 2. Робітник обслуговує чотири однакових верстата. Ймовірність того, що будь-який верстат протягом години потребує уваги робітника, дорівнює 0,6. Припускаючи, що виходи з ладу будь-якого верстата ніяк не пов'язані між собою, знайти ймовірність того, що протягом години: а) усі чотири верстати потребують уваги робітника; б) жоден з верстатів не потребує уваги робітника.
а) Позначимо через А>1>, А>2>, А>3>, А>4> події, які полягають в тому, що протягом години потребують уваги робітника відповідно перший, другий, третій, четвертий верстати. Події А>1>, А>2>, A>3>, А>4> є незалежними. Тому за формулою (3) дістанемо

б) Імовірність того, що протягом години верстат (будь-який) не потребуватиме уваги робітника, знайдемо за правилом відшукання ймовірності протилежної події:


§11. Формула повної ймовірності
Припустимо, що подія A може настати тільки разом з однією із попарно несумісних подій H>1>, H>2>,... Н>п>, які утворюють повну групу подій (рис. 307).
Теорема. Ймовірність події A, яка може настати лише за умови появи однієї із попарно несумісних подій Н>1>, H>2>, ... Н>п>, які утворюють повну групу, визначається за формулою
Р(А) = Р(А/Н>1>)·Р(Н>1>) + Р(А/Н>2>) ·Р(Н>2>) + ...+ Р(А/Н>п>) ·Р(Н>п>). (1)
Якщо подія А відбулася разом з однією із подій H>1>, H>2>,... Н>п>, то це означає, що відбулася одна із попарно несумісних подій A∩H>1>, A∩ H>2>,... A∩Н>п>. Отже,

Тому, застосовуючи теорему про додавання ймовірностей несумісних подій, дістаємо

За теоремою множення довільних подій маємо

Підставивши рівність (3) у рівність (2), дістаємо рівність (1). Формулу (1) називають формулою повної ймовірності.
Приклад 3. Із першого автомата на конвеєр надходить 20 % деталей, з другого - 30 %, з третього - 50 %. Перший автомат дає в середньому 0,2 % бракованих деталей, другий - 0,3 %, третій - 0,1 %. Яка ймовірність того, що на конвеєр надійшла бракована деталь?
Позначимо події: Н>1> - дана деталь виготовлена першим автоматом, H>2> - дана деталь виготовлена другим автоматом, H>3> - дана деталь виготовлена третім автоматом, А - деталь, що надійшла на конвеєр, бракована.
За умовоюP(Н>1>) = 0,2; Р(H>2>) = 0,3; Р( Н>3>) = 0,5; Р(А/Н>1>) = 0,002; Р(А/Н>2>) = 0,003; Р(А/Н>3>) = 0,001.
За формулою повної ймовірності
P(А) = 0,002-0,2 + 0,003-0,3 + + 0,0010,5 = 0,0018.

§ 12. Імовірності гіпотез. Формула Байєса
Нехай подія А може настати за умови появи однієї з попарно несумісних подій H>1>, H>2>,... Н>п>, які утворюють повну групу. Через те, що заздалегідь невідомо, яка з цих подій настане, їх називають гіпотезами. Ймовірність появи події А визначається за формулою повної ймовірності.
Припустимо, що проведено випробування, внаслідок якого відбулася подія А. Виникає питання: як змінились (за умови того, що подія А вже відбулася) ймовірності гіпотез? Відповідь на це питання дає така теорема.
Теорема Байєса. Нехай H>1>, H>2>,... Н>п> - повна група попарно несумісних подій. Тоді

За теоремою множення довільних подій

Ліві частини рівностей (2) і (3) є однаковими. Тому рівними будуть і праві частини цих рівностей, тобто

звідки

Оскільки за формулою повної ймовірності

то, підставивши рівність (5) у рівність (4), дістанемо рівності (1).
Формули (1) називають формулами Байсса. Формули Байєса дають змогу переоцінити ймовірність гіпотез H>1>, H>2>,... Н>п> після того, як проведено випробування, внаслідок якого відбулася подія А. При цьому ймовірності Р(Н>k>) називають апріорними ( a priori - до досліду), а ймовірності Р(Н>k> / А) - апостеріорними (a posteriori - після досліду).
Приклад. У групі з 10 учнів, які прийшли на екзамен, 3 підготовлені відмінно, 4 - добре, 2 - посередньо і 1 - погано. Екзаменаційні білети містять 20 питань. Відмінно підготовлений учень у змозі відповісти на всі 20 питань, добре підготовлений - на 16, посередньо - на 10, погано - на 5. Учень, якого викликали, відповів на три довільно поставлених питання. Знайти ймовірність того, що цей учень підготовлений: а) відмінно; б) погано, х
Позначимо: А - учень відповів на три питання. Гіпотези: Н>1> - учень, підготовлений відмінно, H>2> - учень, підготовлений добре, H>3> - учень, підготовлений посередньо, H>4> - учень, підготовлений погано.
Ймовірності гіпотез до екзамену

§ 13. Повторні випробування. Формула Бернуллі
Коли виконуються послідовні випробування, то за результатом кожного з них може відбутися або не відбутися деяка подія A.
Нехай проводиться п випробувань (одноразових експериментів), причому ймовірність настання події А у кожному випробуванні Р(А) = р і не залежить від результатів інших випробувань. Такі випробування називаються незалежними. Оскільки ймовірність настання події А в одному випробуванні дорівнює p, то ймовірність її ненастання Р(Ặ) = 1 - р = q.
Знайдемо ймовірність того, що при п випробуваннях подія А настане рівно k разів (0<k<п). Виконавши п послідовних випробувань, матимемо різні комбінації результатів. Ті комбінації результатів, в яких подія відбудеться к разів, називатимемо сприятливими.
Визначимо ймовірність Р однієї сприятливої комбінації. Сприятливою комбінацією є добуток п незалежних у сукупності подій: k появ події Ặ і п - k появ події Ặ. Отже, за теоремою про ймовірність добутку подій, незалежних у сукупності, дістанемо, що ймовірність однієї сприятливої комбінації дорівнює

Здійснення складної події, яка полягає в тому, що подія А настає рівно k разів, рівносильна появі принаймні однієї сприятливої комбінації. Іншими словами, така складна подія є сумою всіх сприятливих комбінацій. Проте сприятливі комбінації попарно несумісні. Тому за теоремою про додавання ймовірностей попарно несумісних подій дістанемо ймовірність появи події А k разів при п випробуваннях:

де N - кількість усіх можливих комбінацій.
Залишається визначити N. Розглянемо спочатку приклад.
Нехай п = 3, k = 2. Сприятливими тут є такі комбінації результатів випробувань, коли з трьох випробувань подія А відбувається двічі. Позначатимемо появу події А знаком "+", а появу події Ặ знаком "-". Тоді сприятливі комбінації можна зобразити у вигляді рядків такої таблиці:
|
1 |
2 |
3 |
|
- |
- |
- |
|
+ |
+ |
- |
|
+ |
- |
+ |
|
- |
+ |
+ |
Очевидно, сприятливих комбінацій може бути стільки, скільки різних рядків у цій таблиці, а їх буде стільки, скількома способами можна розмістити два знаки "+" у трьох клітинках, тобто треба кожного разу з трьох клітинок вибрати дві. Очевидно, це можна зробити C3>2>способами. Отже, у цьому разі буде C3>2> сприятливі комбінації результатів випробувань.
Повернемося до загального випадку. Кількість усіх можливих сприятливих комбінацій N = Ck>n> . Підставивши це у формулу (2), матимемо

Формулу (3) називають ще формулою Бернуллі.
Приклад 1. Імовірність виготовлення стандартної деталі дорівнює 0.95. Яка ймовірність того, що серед десяти деталей: а) лише одна нестандартна; б) не більше однієї нестандартної?
а) Нехай подія А полягає в тому, що серед десяти деталей лише одна нестандартна. Тоді маємо п = 10, k = 1, р = 0,05 . За формулою (3)

б) Нехай подія В полягає в тому, що серед десяти деталей не більше однієї нестандартної. Тоді

За умовою шукана ймовірність Р = Р(А U В). Події А і В несумісні, тому Р = Р(А) + Р(В). Отже,

Приклад 2. Що більш імовірно: виграти у рівного собі гравця в шахи 4 партії з 8 чи 3 партії з 5? Нічиї виключаються. Позначимо першу подію А, другу - В. Тоді маємо

Отже, Р(В)>Р(А).
Набір чисел Р>п>(k), де k = 1, 2, ..., п, називається біноміальним розподілом. Він залежить від двох параметрів: п, р.
Властивості:

2) Р>n> (k) спочатку зростають до якогось найбільшого значення, а спадають:

Найімовірніше число успіхів λ в схемі Бернуллі задовольняє нерівності

Приклад 3. Гральний кубик підкидають 35 разів. Яке найімовірніше число появи грані з одним очком?

Отже, дістали два значення: λ = 5 , λ = 6.
§ 14. Граничні теореми Бернуллі
При досить великій кількості випробувань n безпосереднє обчислення ймовірності Р>п> (k) за формулою Бернуллі ускладнюється. Для спрощення обчислень Р>п>(k) запропоновано ряд наближених формул.
Теореми, в яких наводяться такі формули, називаються граничними теоремами схеми Бернуллі.
Локальна теорема Лапласа. Якщо ймовірність р появи події А у кожному випробуванні стала (0<р<1), то ймовірність Р>п>(k) того, що подія А з'явиться k разів у п незалежних випробуваннях, наближено дорівнює (тим точніше, чим більше п)

Значення функції φ(x) знаходять за таблицями (див. додатки, табл. 4).

Деякі властивості функції φ (x):
1) визначена на всій числовій осі;
2) парна, тобто φ (-x) = φ (x)

Графік функції Гаусса наведено на рис. 308.
Приклад 1. Знайти ймовірність того, що з 500 висіяних насінин не зійде 130, якщо схожість насіння оцінюється ймовірністю 0,75.


Графік функції Лапласа наведено на рис. 309.
Приклад 2. Ймовірність появи події в кожному зі 100 незалежних випробувань дорівнює р = 0,8. Знайти ймовірність того, що подія з'явиться не менш як 70 разів.
Вимога, щоб подія з'явилася не менше, ніж 70 разів, означає, що подія може з'явитися або 70 разів, або 71 раз, ... , або 100 разів. Отже, в даному випадку покладемо k>1>, =70, k>2> =100 і скористаємося інтегральною теоремою Лапласа. Тоді

За таблицею значень Ф(х) знаходимо Ф(-2,5) = -Ф(2,5) = -0,4938; Ф(5) = 0,5 . За формулою (2) дістанемо

Теорема Пуассона. Якщо в схемі Бернуллі пр = λ - стала, то

Застосовується теорема при пр < 10 у вигляді наближеної формули для великих значень п (не менше кількох десятків) та малих р ( р < 0,1):

Пуассона.
Приклад 3. Молокозавод відправив у магазин 500 пакетів молока. Ймовірність пошкодження пакета при транспортуванні дорівнює 0,002. Знайти ймовірність того, що при транспортуванні буде пошкоджено пакетів: 1) три; 2) менше трьох; 3) більше трьох; 4) хоча б один.
Число п = 500 велике, ймовірність р = 0,002<0,1, події (пошкодження пакетів) незалежні; тому можна скористатися формулою Пуассона (3).
1) λ = пр = 500 · 0.002 = 1. Ймовірність того, що буде пошкоджено,

2) ймовірність того, що буде пошкоджено менше трьох пакетів,

3) події "пошкоджено більше трьох пакетів" та "пошкоджено не більше " є протилежними, тому
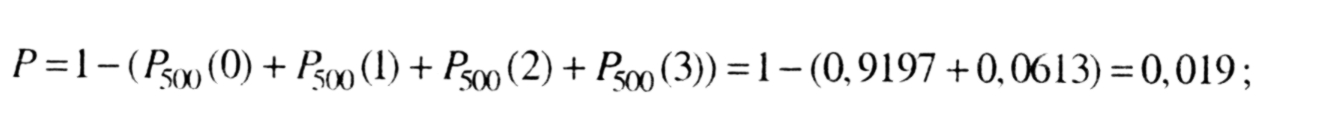
4) подія "пошкоджено хоча б один пакет " є протилежною до події "жоден пакет не пошкоджено." Тому шукана ймовірність того, що буде пошкоджено хоча б один пакет, дорівнює

§ 15. Випадкові величини
Одним із основних понять теорії ймовірностей є поняття випадкової величини, з яким пов'язане уявлення про результати деякого випробування, що полягає у вимірюванні певної числової величини. Величина, яка цікавить дослідника, може набувати різних значень залежно від випадкових обставин. Прикладами випадкових величин можуть бути кількість очок, що випадають на грані гральної кості, кількість викликів, що надходять протягом певного протяжку часу, кількість новонароджених за добу в деякій місцевості, час безвідмовної роботи приладу, дальність польоту ракети тощо. Якщо в результаті експерименту величина набуває лише одного можливого числового значення, заздалегідь невідомого і обумовленого випадковими причинами, то її називають випадковою. Отже, випадкова величина є числом, яке ставиться у відповідність кожному можливому наслідку експерименту.
Означення 1. Випадковою величиною називається числова функція, визначена в просторі елементарних подій.
Означення 2. Випадкова величина називається дискретною, якщо її значення можна записати у вигляді послідовності (скінченної або нескінченної).
Випадкові величини позначаються великими латинськими літерами X, Y, Z, а їх значення відповідними малими літерами.
Якщо випадкова величина X набуває значень х>1>,х>2>, ... , х>п> з відповідними ймовірностями р>1>,р>2>, … , р>n>, то говорять, що задано закон розподілу ймовірностей випадкової величини. Закон розподілу дискретної випадкової величини зручно записувати у вигляді таблиці:
|
X |
х>1> |
Х>2> |
… |
Х>n> |
|
P |
р>1> |
р>2> |
… |
р>n> |
де р>к> = P(x = x>k>)>0, k = 1,...,n .
Враховуючи, що в одному випробуванні випадкова величина набуває лише одного можливого значення, зробимо висновок, що події X =х>1>, X =х>2>, ... , X = х>п> утворюють повну групу, а тому

Означення 3. Дві випадкової величини називаються незалежними, якщо закон розподілу однієї з них не залежить від того, яких можливих значень набуває інша випадкова величина. У противному разі випадкові величини залежні.
Наведемо деякі приклади дискретних випадкових величин та їх розподілів.
1. Рівномірний дискретний розподіл: випадкова величина набуває п різних значень з імовірністю 1/n кожне.
2. Біноміальний розподіл.
3. Розподіл Пуассона.
4. Геометричний розподіл: проводяться незалежні випробування з імовірністю успіху р.
X- кількість спроб до першої появи події A, тобто до успіху; q = 1- р. Закон розподілу подається таблицею:
|
X |
0 |
1 |
2 |
… |
n |
… |
|
p>i> |
p |
qp |
q2p |
… |
qnp |
… |
5. Гіпергеометричний розподіл. Нехай в партії N виробів, із них п -бракованих. N -п - якісних. Навмання вибирають k виробів. Знайти закон розподілу величини X - кількість бракованих виробів серед k.

Приклад 1. Вибираємо навмання одне з натуральних чисел від 1 до 10 і підраховуємо кількість його натуральних дільників X. Знайти закон розподілу випадкової величини X.
Складемо спочатку таблицю кількості дільників натуральних чисел:
|
Ω |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
X |
1 |
2 |
2 |
3 |
2 |
4 |
2 |
4 |
3 |
4 |
Вибір будь-якого числа від 1 до 10 є рівноможливим, тому ймовірність його вибору дорівнює 0,1. Об'єднавши результати, що відповідають однаковій кількості дільників, і додавши їх імовірність, знайдемо закон розподілу X:
|
X |
1 |
2 |
3 |
4 |
|
р |
0,1 |
0,4 |
0.2 |
0,3 |
Контроль: 0,1 + 0,4 + 0,2 + 0,3 = 1.
Закон розподілу повністю характеризує дискретну випадкову величину, але він може бути невідомим; тоді корисними є деякі сталі величини, які дають уявлення про випадкову величину. Такі сталі величини називають числовими характеристиками випадкових величин. Серед числових характеристик особливе значення має математичне сподівання.
Означення 4. Математичним сподіванням ( або середнім значенням ) дискретної випадкової величини X називається число, яке дорівнює сумі добутків усіх її можливих значень на відповідні ймовірності:

Нехай випадкова величина може набувати значень x>1>, .x>2>, ... , х>п> і всі її значення однаково ймовірні. Тоді ймовірність кожного з них р = 1/p .
Математичне сподівання цієї випадкової величини

Отже, в даному разі математичним сподіванням випадкової величини є середнє арифметичне всіх її можливих значень. У загальному випадку математичне сподівання випадкової величини не буде середнім арифметичним всіх її можливих значень. Проте в деякому розумінні його можна розглядати саме так. Справа в тому, що в задачах практичного спрямування закон розподілу випадкової величини є невідомим. Тому виконують велику кількість випробувань або спостережень, кожне з яких відбувається у приблизно однакових умовах. Таку сукупність спостережень називають вибіркою із значень, яких набуває дана величинах
Нехай у вибірці з п спостережень за випадковою величиною X ця величина п>1> разів набувала значення х>1>, … ; п>2> разів - значення х>2>,... ; n>k> разів-значення x>k>, причому п>1> + п>2> +... + n>k>> >= n. Тоді сума всіх значень, які спостерігались, дорівнює x>1>n>1 >+ x>2>n>2> +... + x>k>n>k>. Величина

називається вибірковим середнім.
п. Зауважимо, що відношення n>1>/n є відносною частотою значення х>1>, n>2>/n є відносною частотою значення х>2>, n>k>/n є відносною частотою значення х>k>, причому відношення n>1>/n, n>2>/n,…, n>k>/n змінюються від вибірки до вибірки.
Проте за достатньо великої кількості спостережень п маємо наближені рівності

Це означає, що математичне сподівання наближено дорівнює (тим точніше, чим більше число спостережень) вибірковому середньому.
Властивості математичного сподівання:

Точку з координатою М(Х) називають центром розсіяння ймовірностей. Випадкову величину X – М(Х) називають відхиленням. Різні випадкові величини можуть мати одне й те саме математичне сподівання. Тому виникає потреба розглянути ще одну числову характеристику для вимірювання ступеня розсіяння випадкової величини навколо її математичного сподівання.
Означення 5. Дисперсією випадкової величини називається математичне сподівання квадрата відхилення цієї випадкової величини.
Позначається дисперсія D(X). Отже,

Поряд з дисперсією розглядають також характеристику, яка вимірюється в тих самих одиницях, що і випадкова величина.
Означення 6. Середнім квадратичним відхиленням випадкової величини X називається корінь квадратний з її дисперсії:

Приклад 2. Знайти числові характеристики випадкової величини, яку розглянуто у прикладі 1:

Теорема (формула обчислення дисперсії). Дисперсія випадкової величини X дорівнює різниці між математичним сподіванням квадрата і квадратом математичного сподівання цієї випадкової величини:

де x>1>, .x>2>, ... , х>k> різні значення випадкової величини, що спостерігаються; n>1>, n>2>, ... , n>k> - їхні частоти; п = n>1> +п>2> +... + п>k> - загальна кількість спостережень; х - вибіркове середнє. Величину S називають вибірковим середнім квадратичним, або стандартним відхиленням.
§ 16. Закон великих чисел
У цьому параграфі розглянемо теореми про поводження суми великої кількості випадкових величин. Виявляється, що за деяких порівняно загальних умов сумарна поведінка досить великої кількості випадкових величин майже втрачає випадковість і набуває закономірності. Наприклад, відносна частота події наближено дорівнює її ймовірності при достатньо великій кількості випробувань, середнє арифметичне незалежних спостережень випадкової величини при великій кількості спостережень наближено дорівнює математичному сподіванню цієї величини. Тому під законом великих чисел в теорії ймовірностей розуміють теореми, в кожній з яких йдеться про наближення середніх характеристик великого числа випробувань до деяких певних сталих. При доведенні теорем, які об'єднують єдиною назвою "закон великих чисел", а також при розв'язуванні багатьох практичних задач використовують таку нерівність:

де ε >0 - довільне число.
Нерівність (1) називають нерівністю Чебишова. Нерівність Чебишова дозволяє оцінити ймовірність відхилень значень випадкової величини від свого математичного сподівання.
Теорема Чебишова (закон великих чисел). Нехай Х>1>,Х>2>, ... , Х>п>, ... - послідовність попарно незалежних випадкових величин, що задовольняють такі умови:

Перейшовши до границі при n → ∞ в нерівностях (4), дістанемо рівність (2), яка означає, що середнє арифметичне значень попарно незалежних випадкових величин, коли кількість доданків нескінченно зростає, є збіжним за ймовірністю до середнього арифметичного їх математичних сподівань.

Для практичного використання теорему Чебишова можна тлумачити так: коли попарно незалежні випадкові величини мають однакове математичне сподівання і обмежені дисперсії, то для досить великих п з будь-якої точністю має місце наближена рівність

Практичне значення теореми Чебишова можна ілюструвати таким прикладом. Нехай за допомогою вимірювального приладу багато разів вимірюється значення деякої фізичної величини, причому результат кожного вимірювання не залежить від результатів решти. Послідовні результати вимірювань - це випадкові величини Х>1>,Х>2>, ... , Х>п>. Вимірювання виконується без систематичних (одного знаку) похибок. Це означає, що математичні сподівання усіх випадкових величин є однаковими і дорівнюють істинному значенню шуканого виміру а, тобто M(X>i>) =а(і =1, 2,...,n).
Якщо прилад дає можливість вимірювати з певною точністю, то це означає, що дисперсії результатів вимірювання є обмеженими. Отже, виконуються умови теореми Чебишова, а тому згідно з формулою (5) маємо

Таким чином, обчислюючи середнє арифметичне значень вимірювань, з великою ймовірністю можна вважати, що це середнє арифметичне результатів як завгодно мало відрізняється від істинного значення вимірюваної фізичної величини.
Як наслідок, з теореми Чебишова можна отримати наступне твердження.
Теорема Бернуллі. Нехай k - кількість успіхів у п випробуваннях Бернуллі, а р (0< р<1) - ймовірність успіху в кожному випробуванні. Тоді для довільного ε > 0 виконується рівність

Рівність (6) можна тлумачити так: коли виконується багато незалежних випробувань, то з імовірністю, що відносна частота появи події (число k/n) мало відрізняється від імовірності p події А.
У багатьох випадках на практиці число p буває невідомим. Із теореми Бернуллі випливає, що відносну частоту появи події А (число k/n) при достатньо великому п можна взяти за ймовірність події. Теорема Бернуллі є найпростішою формою закону великих чисел.