Основные задачи вычислительной математики
Основные задачи вычислительной математики. Теория погрешностей. Приближённое вычисление значений функций заданных аналитически. Оценка погрешности вычислений.
Работа современного инженера, физика и любого другого исследователя связана с моделированием сложных процессов, происходящих в разных областях знаний и деятельности человека. Зачастую, моделирование является средним звеном в разработке проекта и его внедрения в производство. Процесс проектирования можно представить схематически: (рис 1).
Осознание потребности
Разработка проекта
Построение модели
Изучение свойств модели
Внедрение в производство







Итерационный цикл
Доработка проекта


рис 1.
Для исследования свойств построенной математической модели, в большинстве случаев, не удаётся аналитически решить задачу. Поэтому, вступают в силу методы вычислительной математики, которые позволяют решение каждой задачи довести до числового результата и оценить точность производимых вычислений.
При работе с приближёнными величинами приходится решать следующие задачи:
а) давать математические характеристики точности приближённых величин;
б) оценивать точность результата, когда известна точность исходных данных;
в) находить точность исходных данных, обеспечивающую заданную точность результата;
г) согласовывать точность исходных данных с тем, чтобы не затрачивать излишней работы при отыскании или вычислении одних данных, если другие данные слишком грубы;
а)
Определение: абсолютная погрешность -
это абсолютная величина разности между
точным значением величины
 и её приближённым значением
и её приближённым значением
 :
:
 (1.1)
(1.1)
Здесь следует различать два случая:
точное
значение числа
 нам известно, что на практике очень
редко, тогда пользуемся формулой (1.1).
нам известно, что на практике очень
редко, тогда пользуемся формулой (1.1).
Пример
1: а=5.129 а*=5.128, тогда
 ;
;
-
точное значение числа
 неизвестно, тогда вводят понятие
предельной абсолютной погрешности.
неизвестно, тогда вводят понятие
предельной абсолютной погрешности.
Определение: предельной абсолютной погрешностью приближённого числа называют всякое число, не меньшее абсолютной погрешности этого числа.
Таким
образом, если
 - предельная абсолютная погрешность
приближённого числа
- предельная абсолютная погрешность
приближённого числа
 ,
то
,
то
 (1.2)
(1.2)
отсюда следует, что
 (1.3)
(1.3)
Значение предельной абсолютной погрешности, обычно, подбирается интуитивно по смыслу задачи.
Пример
2: Определить предельную абсолютную
погрешность числа
 ,
заменяющего число
,
заменяющего число
 ,
точное значение которого нам неизвестно.
,
точное значение которого нам неизвестно.
Так
как мы знаем, что
 ,
то можем утверждать:
,
то можем утверждать:
 (1.4)
(1.4)
и,
следовательно,
 ,
т.е. можем сказать, что
,
т.е. можем сказать, что
 (1.5)
(1.5)
Понятия абсолютной погрешности и предельной абсолютной погрешности, хотя и дают представление о точности вычислений, однако не всегда достаточны.
Например: если при измерении длины стержней получены результаты: <l1 и l2>, то, несмотря на совпадение предельных абсолютных погрешностей, качество первого измерения выше второго, т.к. если погрешность близка по величине от самого приближённого числа, то точность этого измерения недостаточна. Изданного примера понятно, что для оценки качества измерения, нам нужна абсолютная погрешность, приходящаяся на единицу длины. Такая погрешность носит название относительной погрешности.
Определение:
относительной погрешностью
 приближённого числа
приближённого числа
 называется отношение абсолютной
погрешности
называется отношение абсолютной
погрешности

 этого числа к модулю соответствующего
точного числа
этого числа к модулю соответствующего
точного числа

 :
:
 (1.6)
(1.6)
Поскольку
точное значение величины
 нам часто не известно, то рассмотрим
понятие предельной относительной
погрешности
нам часто не известно, то рассмотрим
понятие предельной относительной
погрешности
 .
.
Определение:
предельной относительной погрешностью
 данного приближённого числа
данного приближённого числа
 называется всякое число, не меньшее
относительной погрешности этого числа:
называется всякое число, не меньшее
относительной погрешности этого числа:
 (1.7)
(1.7)
Отсюда следует, что
 (1.8)
(1.8)
т.е.
 (1.9)
(1.9)
но, как известно:
 (1.10)
(1.10)
Сопоставление
формул (1.9) и (1.10) даёт соотношение между
предельной абсолютной
 погрешностью и предельной относительной
погрешностью
погрешностью и предельной относительной
погрешностью
 :
:
 (1.11)
(1.11)
Из
этой формулы иногда выражают
 и пишут:
и пишут:
 (1.12)
(1.12)
Рассмотрим примеры:
Пример
3: Вес 1 дм3
воды при
 равен
равен
 г.
Определить предельную относительную
погрешность результата взвешивания.
г.
Определить предельную относительную
погрешность результата взвешивания.
Решение:
очевидно, что предельная абсолютная
погрешность
 г. и
г. и
 ,
следовательно:
,
следовательно:
 (1.13)
(1.13)
Пример
4: При определении газовой постоянной
для воздуха, получили
 .
Зная, что относительная погрешность
этого значения
.
Зная, что относительная погрешность
этого значения
 ,
найти пределы, в которых заключается
R.
,
найти пределы, в которых заключается
R.
Решение:
имеем:
 ,
тогда
,
тогда
 ,
т.е.
,
т.е.
 (1.14)
(1.14)
Теперь займёмся изучением распространения погрешностей из-за арифметических действий.
б)
Рассмотрим функцию
 ,
пусть значения переменных
,
пусть значения переменных
 ,
вычислены приближённо, где
,
вычислены приближённо, где
 соответствующие абсолютные погрешности.
соответствующие абсолютные погрешности.
Нас
интересует абсолютная и относительная
погрешности вычисленных значений
функции
 .
.
По
определению видно, что абсолютная
погрешность функции
 имеет вид:
имеет вид:
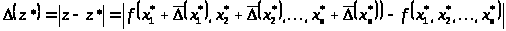
обычно
 ,
поэтому, раскладывая в ряд Тейлора,
можно ограничиться лишь линейными
членами по
,
поэтому, раскладывая в ряд Тейлора,
можно ограничиться лишь линейными
членами по
 .
Получаем:
.
Получаем:
 (1.15)
(1.15)
Отсюда получаем оценку:
 (1.16)
(1.16)
Тогда для предельных абсолютных погрешностей имеем:
 (1.17)
(1.17)
Разделив
обе части (1.17) на
 ,
получаем предельную относительную
погрешность при вычислении функции
,
получаем предельную относительную
погрешность при вычислении функции
 ,
в точке
,
в точке
 :
:
 (1.18)
(1.18)
Или записывая более компактно:
 (1.19)
(1.19)
Эту формулу можно переписать в виде:
 (1.20)
(1.20)
в) Рассмотрим частные случаи:
1.
Пусть
 .
Изучим абсолютные и относительные
погрешности суммы.
.
Изучим абсолютные и относительные
погрешности суммы.
Решение: т.к.
 (1.21)
(1.21)
то из (1.17) получаем
 (1.22)
(1.22)
Также из (1.18) получаем:
 (1.23)
(1.23)

2.
Пусть,
 .
Изучим абсолютные и относительные
погрешности разности
.
Изучим абсолютные и относительные
погрешности разности

Решение:
 ;
;
 ,
поэтому из (1.17) имеем
,
поэтому из (1.17) имеем
 (1.24)
(1.24)
А из (1.18) получаем:
 (1.25)
(1.25)
Ясно,
что если
 и
и
 близкие друг к другу числа, то
близкие друг к другу числа, то
 очень малое число, т.е. абсолютная
погрешность разности будет очень большим
числом. Поэтому при вычислениях, где
это возможно, нужно избегать вычитания
близких друг к другу чисел.
очень малое число, т.е. абсолютная
погрешность разности будет очень большим
числом. Поэтому при вычислениях, где
это возможно, нужно избегать вычитания
близких друг к другу чисел.
Например,
если нам нужно вести вычисления по
формуле:
 - объём между двумя сферами, где
- объём между двумя сферами, где
 - очень малое число. Здесь лучше избавиться
от вычитания и пользоваться аналогичной
формулой
- очень малое число. Здесь лучше избавиться
от вычитания и пользоваться аналогичной
формулой
 ,
тем самым, обходя вычитание близких
чисел, которое может быть больше
относительной погрешности вычислений.
,
тем самым, обходя вычитание близких
чисел, которое может быть больше
относительной погрешности вычислений.
3. Изучим погрешности произведения чисел.
 (1.26)
(1.26)
 (1.27)
(1.27)
отсюда очевидно, что
 (1.28)
(1.28)
 (1.29)
(1.29)
Таким образом, при умножении приближённых чисел, относительные погрешности складываются.
4. Рассмотрим погрешности деления чисел.
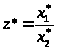 (1.30)
(1.30)
 ,
,
 (1.31)
(1.31)
Поэтому
 (1.32)
(1.32)
 (1.33)
(1.33)
Из вышеизложенных частных случаев следует, что при вычислениях на ЭВМ:
нет смысла производить округление перед сложением (т.к. увеличим погрешность);
при вычитании надо всячески избегать разности близких чисел;
если вычисляем произведение чисел с k верными знаками, то в результате будем иметь не менее k-1 верных знаков;
при делении действуют те же правила, что и при умножении, но надо избегать деления на малое число (близкое к нулю).
Вышеизложенная
теория погрешностей основана на
допущении, что
 -погрешности
настолько малы, что их квадратами можем
уже пренебрегать (на этом основано
«обрезание» формулы Тейлора).
-погрешности
настолько малы, что их квадратами можем
уже пренебрегать (на этом основано
«обрезание» формулы Тейлора).
Поэтому все введённые формулы теряют силу, если эти условия нарушены. В таких случаях нужно использовать и квадратичные члены, чтобы получить более точную теорию.
Но надо учитывать, что в этом случае формулы значительно усложняются.
В заключение рассмотрим числовой пример:
Пример
5: Найти предельные абсолютную и
относительную погрешности объёма шара
 ,
если
,
если
 см.,
см.,
 .
.
Решение:
 ;
;
имеем:
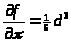 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 (1.34)
(1.34)
 (1.35)
(1.35)
Упражнение:
вывести формулы предельной абсолютной
и относительной погрешностей для функции
 ,
а далее для многочлена
,
а далее для многочлена
 и рациональной функции.
и рациональной функции.
Пример
6: Найти сумму приближённых чисел:
 и
и
 .
.
Решение:

 ,
т.е.
,
т.е.
 .
.
Пример
7: Найти относительную погрешность
разности чисел
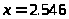 и
и
 ,
если
,
если
 ,
,
т.е.
если

Решение:

Именно поэтому избегают вычитания приближённых значений близких друг к другу чисел.
Пример
8: Найти произведение чисел, если все
знаки верные:
 и
и
 .
.
Решение:
 ,
т.к.
,
т.к.
 и
и
 ,
,
то имеем
 и
и

следовательно
 ,
т.е.
,
т.е.

Окончательно
имеем:
 .
.
Пример
9: Расстояние между двумя пунктами по
прямой равно
 км.
км.
За
какое время звук распространится от
одного пункта до другого в воздухе и по
рельсам, если скорость звука в воздухе
 м/с, а в стали
м/с, а в стали
 м/с?
м/с?
Решение:  (с.);
(с.);  (с.)
(с.)

 ,
,
т.е.
 (с.)
(с.)
 (с.)
(с.)
 (с.)
(с.)
 (с.)
(с.)