Применение методов дискретной математики в экономике
Министерство образования и науки РФ
Государственное образовательное учреждение высшего профессионального образования
«Тихоокеанский Государственный Университет»
Институт экономики и управления
Кафедра Экономическая кибернетика
Специальность 080116 Математические методы в экономике
ПРИМЕНЕНИЕ МЕТОДОВ ДИСКРЕТНОЙ
МАТЕМАТИКИ В ЭКОНОМИКЕ
Курсовая работа по дисциплине
«Дискретная математика»
КР. 030590198
Выполнила:
Студентка группы ММО-31
Рязанова А.В.
Руководитель работы:
Пазюк К. Т.
Хабаровск – 2005
Реферат
Курсовая работа содержит пояснительную записку на 33 листах формата А4, включающую 6 таблиц, 13 рисунков, 9 литературных источников.
БУЛЕВА ФУНКЦИЯ, ВЫСКАЗЫВАНИЯ, ЛОГИЧЕСКИЕ ОПЕРАЦИИ, ТАБЛИЦЫ ИСТИННОСТИ, ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА, КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА, ПОЛИНОМ ЖЕГАЛКИНА, ПРОИЗВОДНАЯ ЛОГИЧЕСКОЙ ФУНКЦИИ, ГРАФ, «ЖАДНЫЙ» АЛГОРИТМ, АЛГОРИТМ ДЕЙКСТРА, ЗАДАЧА КОММИВОЯЖЁРА, НЕЧЕТКОЕ МНОЖЕСТВО, КОНКУРЕНТОСПОСОБНОСТЬ, НЕЧЕТКОЕ ОТНОШЕНИЕ ПРЕДПОЧТЕНИЯ, АЛЬТЕРНАТИВА, СТЕПЕНЬ НЕДОМИНИРУЕМОСТИ
Объект исследования данной курсовой работы: дискретные системы, методы дискретной математики и их применение в области экономики.
Цель работы – ознакомиться с максимально широким кругом понятий дискретной математики и выявить ее основные методы, которые могут использоваться в экономике. Раскрыть взаимосвязь понятий, их внутреннюю логику. Научиться правильно формулировать экономические задачи.
В курсовой работе были рассмотрены и применены: методы математической логики: метод построения таблицы истинности, нахождение полинома Жегалкина методом неопределенных коэффициентов, метод нахождения производных, метод нахождения конъюнктивной и дизъюнктивной нормальной формы; методы теории графов: «жадный» алгоритм, алгоритм Дейкстра, венгерский метод решения задачи коммивояжера; методы теории нечетких множеств: метод многокритериального выбора альтернатив на основе нечеткого отношения предпочтения.
Содержание
Введение
1 Применение логических функций
1.1 Применение методов дискретной математики в экономике
1.2 Практическое применение методов математической логики
2 Применение теории графов
2.1 Практическое применение жадного алгоритма
2.2 Применение алгоритма Дейкстры
2.3 Задача коммивояжера
3 Практическое применение теории нечетких множеств
Заключение
Список использованных источников
Введение
В данной курсовой работе содержится три основных раздела: применение математической логики экономике; применение теории графов в экономике и применение отношения нечеткого предпочтения.
Первая часть данной работы посвящена применению методов дискретной математике и математическому моделированию в экономике и математической логике, где рассматриваются логические операции и преобразование логических функций, приведение функций к дизъюнктивной и конъюнктивной нормальной форме, построение таблицы истинности, нахождение полинома Жегалкина для заданной функции и её производных по одной и двум переменным.
Во второй части подробно рассматривается применение жадного алгоритма, алгоритма Декстры, и задачи коммивояжера на конкретных примерах. Во всех этих задачах требуется найти оптимальный (в данном случае минимальный) маршрут. Большинство понятий, излагаемых в данной главе, широко известны, потому что графы, благодаря своей наглядности и универсальности стали использоваться в экономике. Теория графов широко применяется при решении задач управления производством и экономикой в целом.
В третьей части рассматривается многокритериальный выбор альтернатив на основе нечеткого отношения предпочтений. В курсовой работе показано, как элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости.
1. применение Логических функций
1.1 Применение методов дискретной математики в экономике
При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом рассмотрения в дискретной математике. К ним относятся методы, основанные на теоретико-множественных представлениях, графы, алгоритмы формальные системы, математическая логика.
В экономике существует множество отраслей, использующих методы дискретной математики. Это и эконометрика, и логистика, и математическое моделирование. Так, в эконометрике булевские переменные применяются в исследовании регрессионных моделей с переменной структурой и в построении регрессионных моделей по неоднородным данным. В этом случае рассматривается лишь одно уравнение регрессии, куда вводятся булевские переменные, которые характеризуют изучаемый фактор. Данный метод удобен для выявления зависимости модели от некоторого фактора.
Теория графов широко используется в логистике для описания потоков, задания маршрутов. Так схему дорог удобнее представить в виде ориентированного графа, и известными нам методами выбрать кратчайший путь. В настоящее время, прокладывая маршрут, нельзя не брать во внимание и пропускную способность магистралей, интерпретируя маршруты в графы, можно получить экономически выгодное решение.
При помощи теории нечетких множеств, методом нечеткого предпочтения, можно выбрать конкурентоспособный товар или услугу. Поэтому, данная теория применяется в маркетологии, при исследовании рынков различных экономических благ.
1.2 Практическое применение методов математической логики
Всякая логическая функция «n»
переменных может быть задана таблицей,
в левой части которой перечислены все
2n
наборов значений переменных (то есть
всевозможных наборов двоичных векторов
длины «n»), а в правой части приведены
значения функции на этих наборах. При
любом фиксированном упорядочении
наборов значений переменных логическая
функция «n»
переменных полностью определена
вектор-столбцом своих значений, то есть
вектором длины 2n.
Поэтому число различных логических
функций «n»
переменных будет
 .
В самом деле, для одного набора значений
своих переменных (строка левой части
таблицы) значение функции может быть
либо 1, либо 0 (две возможности). Число же
возможных различных наборов аргументов
функции, как уже отмечалось равно 2n,
поэтому число различных логических
функций будет
.
В самом деле, для одного набора значений
своих переменных (строка левой части
таблицы) значение функции может быть
либо 1, либо 0 (две возможности). Число же
возможных различных наборов аргументов
функции, как уже отмечалось равно 2n,
поэтому число различных логических
функций будет /1/.
/1/.
Заданием в данном пункте является построение таблицы истинности для следующего высказывания:
 ,
,
Высказыванием называется повествовательное предложение, о котором можно сказать в данный момент, что оно истинно или ложно, но не то и другое одновременно. “Истинность” или “ложность” предложения – это истинностное значение высказывания. Каждому высказыванию сопоставляется переменная, равная 1, если высказывание истинно, и равная 0, если оно ложно. Эти высказывания будут считаться простыми. Из простых высказываний с помощью логических связок могут быть построены составные высказывания. В таблице 1 приведены некоторые логические связки, используемые при задании данной функции (1).
Таблица 1-Логические связки
|
Название |
Обозначение |
|
Конъюнкция |
|
|
Импликация |
|
|
Сумма по модулю два |
|
|
Штрих Шеффера |
| |
|
Отрицание |
|
|
Дизъюнкция |
|
|
Стрелка Пирса |
|
Правильно построенные составные высказывания называются (пропозиционарными) формулами. Истинностное значение формулы определяется через истинностные значения её составляющих в соответствии с единой таблицей истинности (таблица 2).
Таблица 2-Истиностные значения формул высказывания
|
Х>1> |
Х>2> |
X>1> X>2> |
X>1> X>2> |
X>1> X>2> |
X>1> X>2> |
X>1> |
X>1> X>2> |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
Для того чтобы составить таблицу истинности для формулы, необходимо выполнить последовательность всех логических операций.
 ,
(1)
,
(1)
После последовательного выполнения всех логических операций составляется таблица истинности для данной функции
Таблица 3- Таблица истинности функции (1)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
x |
y |
z |
& |
> |
|
|
> |
> |
> |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
Приведение функции к конъюнктивным и дизъюнктивным нормальным формам. Конъюнктивным (дизъюнктивным) одночленом от переменных а>1>, а>2>, а>3>,…,а>n> называется конъюнкция (дизъюнкция) этих переменных или их отрицаний. Формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных произведений (конъюнктивных одночленов), называется дизъюнктивной нормальной формой (ДНФ) данной формулы. Формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных произведений (дизъюнктивных одночленов), называется конъюнктивной нормальной формой (КНФ) данной формулы /2/. Справедливы следующие теоремы: любая булева функция, тождественно не равная нулю, представима и притом единственным образом в виде ДНФ по формуле:
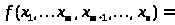 V
V (2)
(2)
Любая булева функция, тождественно не равная единице представима и притом единственным образом в виде КНФ.

 (3).
(3).
Любая булева функция представима формулой, в которую входит только конъюнкция, дизъюнкция и отрицание /2/.
Искомая ДНФ для функции (1) имеет вид:

Искомая КНФ для функции (1) будет иметь следующий вид:

В расчетах ДНФ и КНФ использована методика /2/.
Построение полинома Жегалкина.
Представление булевой функции над базисом {0,1,v,} называется полиномом Жегалкина.
Таким образом, всякая булева функция представима в виде:


где ∑ - сложение по модулю два, знак · обозначает конъюнкцию/7/.
Для функции f(x,y,z)(1) полином Жегалкина имеет вид:
P(x, y, z)=>0>1>1>x>2>y>3>z>4>xy>5>xz>6>yz>7>xyz> >
Метод неопределенных коэффициентов заключается в том, что путем последовательной подстановки переменных x, y, z и соответственно значений функции при этих переменных, из таблицы 1 в данный полином (4), строится система уравнений:
0 =>0>1>1>0>2>0>3>0>4>00>5>00>6>00>7>000
=>0>1>1>0>2>0>3>0>4>00>5>00>6>00>7>000
0=>0>1>1>0>2>0>3>1>4>00>5>01>6>01>7>001
1=>0>1>1>0>2>1>3>0>4>01>5>00>6>10>7>010
0=>0>1>1>0>2>1>3>1>4>01>5>01>6>11>7>011
0=>0>1>1>1>2>0>3>0>4>10>5>10>6>00>7>100
0=>0>1>1>1>2>0>3>1>4>10>5>11>6>01>7>101
0=>0>1>1>1>2>1>3>0>4>11>5>10>6>10>7>110
0=>0>1>1>1>2>1>3>1>4>11>5>11>6>11>7>111
По свойству суммы по модулю два находится :
>0>=0, >1>=0, >2>=1, >3>=0, >4>=1, >5>=0, >6>=1, >7>=1
Полином Жегалкина будет иметь вид:
(x, y, z) = y xy yz xyz> >
Правильность построения полинома проверяется таблицей истинности:
Таблица 4 - Таблица истинности для полинома Жегалкина
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
x |
y |
z |
x&y |
|
y&z |
|
x&y&z |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Дифференцирование функции нескольких переменных.
Производной булевой функции
(xn)
по совокупности переменных
переменных
 называется функция:
называется функция:


На основе данной формулы (5) находится производная по одной переменной x


Для данной функции (1) производная по формуле (6) принимает вид:


Таблица 5 - Производная ∂⁄∂x для формулы(7)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
x |
y |
z |
|
& |
> |
|
|
> |
> |
> |
> |
|
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
Вектор значений функции (7) имеет вид:

Производная по двум переменным находится также по формуле (5):


Для данной функции (1) производная принимает вид:


Таблица 6 - Производная ∂2⁄∂(x;y) для формулы(9)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
x |
|
|
& |
> |
|
|
> |
> |
> |
> |
|
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
Вектор значений функции (6) имеет вид:

2. Применение теории графов
2.1 Практическое применение жадного алгоритма
На территории некого города N размещены заводы и магазины, в которые поставляется продукция с этих заводов. В результате разработки были определены возможные трассы для прокладки коммуникаций и оценена стоимость их создания для каждой трассы. Стоимость прокладки коммуникаций для трассы между заводом №1 и магазином удобрений составляет 15 у.е., между заводом №1 и заводом №3 – 85 у.е., между заводом №1 и хлебозаводом – 20 у.е. Между магазином №1 и заводом №2 составит 25 у.е., между магазином №1 и обувной фабрикой – 65 у.е. Стоимость прокладки коммуникаций для трассы, соединяющей хлебозавод и магазин №2 - 5 у.е., между хлебозаводом и кафе – 50 у.е., между заводом №2 и кафе - 20 у.е., между магазином №2 и продуктовым магазином - 20 у.е., между продуктовым магазином и обувной фабрикой - 25 у.е, между продуктовым магазином и кафе – 35 у.е., между обувной фабрикой и магазином №3 - 15 у.е, между обувной фабрикой и аптекой – 40 у.е., между кафе и аптекой - 10 у.е., между магазином №3 и торговым центром - 20 у.е., между аптекой и заводом №3 составит 30 у.е, между аптекой и торговым центром – 45 у.е., между заводом №3 и торговым центром, - 25 у.е. Необходимо, чтобы коммуникации связали все объекты, затраты на прокладку данных коммуникаций должны быть минимальны.
Для удобства записи вводятся следующие обозначения:
V>1 >– завод №1, V>2 >– магазин №1, V>3 >– хлебозавод, V>4 >–завод №2, V>5 >– магазин №2 V>6 >–продуктовый магазин, V>7 >– обувная фабрика, V>8 >–кафе, V>9 >– магазин №3, V>10 >– аптека, V>11 >–завод №3, V>12 >– торговый центр.
Если создать графическую интерпретацию данной модели, то видно что получился граф с 12 вершинами и 18 ребрами.

Рисунок 1– Графическая интерпретация задачи о оптимальной структуре сети
Из вышесказанного следует, что данную экономическую задачу можно решить с помощью теории графов. Требуется найти дерево покрытия минимального веса. Задача решается с помощью разновидности «жадного» алгоритма, алгоритма Краскала.
Пусть имеется конечное множество Е, |E|=18, весовая функция w: ER+ и семейство ℇ⊂ 2Е. Требуется найти ХЕ, такое что :
Пусть Е – непустое конечное множество, w: ER+ - функция, ставящая в соответствие каждому элементу е этого множества неотрицательное действительное число w(e) – вес элемента е. Для Х Е вес w(Х)определим как сумму весов всех элементов множества Х:

где

Другими словами, необходимо выбрать в данном семействе непустое подмножество наименьшего веса.
Сопоставим каждому пункту сети вершину графа G. А каждому ребру этого графа сопоставим число, равное стоимости строительства соответствующей коммуникации: (рисунок 1).
Примером жадного алгоритма служит алгоритм Краскала /3/.
Существует теорема, которая утверждает, что алгоритм Краскала всегда приводит к ребру, имеющему минимальный вес.
Согласно алгоритму Краскала, выбирается ребро минимального веса. В данном случае это будет ребро е>1> = {3,5}, получаем граф Т>1>.
Строится граф Т>2> = Т>1> + е>2>, где е>2> - ребро, имеющее минимальный вес среди ребер, не входящих в Т>1> и не составляющий циклов с ребрами Т>1>, е>2 >{8,10}.
Т>3> = Т>2> + е>3>, где е>3> = {7,9}.
Т>4> = Т>3> + е>4>, где е>4> = {1,2}.
Т>5> = Т>4 >+ е>5>, где е>5> = {1,3}.
Т>6> = Т>5> + е>6>, где е>6> = {5,6}.
Т>7> = Т>6> + е>7>, где е>7> = {4,8}.
Т>8> = Т>7> + е>8>, где е>8> = {9,12}
Т>9> = Т>8> + е>9>, где е>9> = {2,4}.
Т>10> = Т>9 >+е>10>, где е>10> = {6,7}.
Т>11> = Т>10> + е>11>, где е>11> = {11,12}.
Найдено минимальное дерево покрытия взвешенного графа, следовательно, найдена и оптимальная структура сети, где общая стоимость затраченная на прокладку коммуникаций составит:

и это минимальная сумма затрат из всех возможных. При прокладке коммуникационной сети, соединяющей все данные пункты затрачивается 200 у.е.

Рисунок 2 – Решение задачи о оптимальной структуре сети
Коммуникации проложат между следующими пунктами: аптека – кафе - завод №2 – магазин №1 - завод №1 – хлебозавод – магазин №2 - продуктовый магазин – обувная фабрика – магазин №3 – торговый центр.
2.2 Применение алгоритма Дейкстры
Фирме, занимающейся перевозкой скоропортящихся товаров, необходимо доставить товар из Суйфэньхе в Хабаровск, причем маршрутов, по которым можно произвести доставку несколько. Расстояние между Суйфэньхе и городом 2 составляет 15 км, между Суйфэньхе и городом 3 – 20 км, между Суйфэньхе и городом 11 – 85 км. Между городом 2 и городом 4 - 25 км, между городом 2 и городом 7 - 65 км. Между городом 3 и городом 5 составляет 5 км, между городом 3 и городом 8 - 50 км. Между городом 4 и городом 8 - 20 км. Между городом 5 и городом 6 - 20 км. Между городом 6 и городом 7 - 25 км, между городом 6 и городом 8 - 35 км. Между городом 7 и городом 9 - 15 км, между городом 7 и городом 10 - 40 км. Между городом 9 и городом 12 - 20 км. Между городом 10 и городом 11 - 30 км, между городом 10 и городом 12 - 45 км. Между городом 11 и городом 12 - 25 км. Требуется найти кратчайший путь из Суйфэньхе в Хабаровск
Строится граф G, в котором город Суйфэньхе обозначается цифрой 1, Хабаровск - 12. Остальные пункты маршрута обозначаются цифрами 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. Каждому ребру графа сопоставляется число, которое будет равняться расстоянию между пунктами. Требуется найти минимальный маршрут. Алгоритм Дейкстры находит кратчайший путь между двумя вершинами в графе /3/. Следовательно, можно воспользоваться им, при решении данной экономической задачи.

Рисунок 3– Графическая интерпретация задачи о нахождении минимального маршрута доставки
Если вершина v лежит на кратчайшем пути от начальной вершины к конечной, то T[v] – длина кратчайшего пути от начальной вершины к конечной.

С помощью алгоритма Дейкстры находится единственный минимальный маршрут, соединяющий вершины 1и 12 графа G (рисунок 3).
Пусть вершина – номер 1 – начальная вершина. Для неё назначается постоянный ярлык L(к) = 0. Конечной вершиной будет считаться вершина номер 1. Рассматриваются вершины, смежные с вершиной 12, и назначим им временные ярлыки: L(2) = 25 , L(3) = 20 , L(11) = 85.
Нужно выбирать вершину с самым маленьким ярлыком – это вершина номер 3, и её ярлык L(3) = 20 становится постоянным.
Повторяя этот процесс для вершины номер 3, вершинам присваиваются временные ярлыки: L(5) = 5 , L(8) = 50.
Среди всех временных ярлыков минимальный будет у L(5) = 5. Этот ярлык становится постоянным.
С вершиной 5 смежна только вершина 6. L(6) = 20.
Повторяя этот процесс для вершины номер 6, вершинам присваиваются временные ярлыки: L(7) = 25 , L(8) = 35.
Среди всех временных ярлыков минимальный будет у L(7) = 25. Этот ярлык становится постоянным.
Повторяя процесс, рассматриваются вершины, смежные с вершиной 7. Это 2, 9 и 10. Для которых временные ярлыки будут: L(2) = 65, L(9) = 15, L(10) = 40. Находится наименьший временный ярлык. Он будет у: L(9) = 20.
С вершиной 9 смежна только вершина 12. L(12) = 20.
Теперь, когда дерево сформировано, мы можем определить самый короткий путь от 1 до 12. Этот путь дерева, соединяющий вершины 1 и 12. И он проходит через вершины 3, 5, 6, 7 и 9. Длина этого пути - L(v') = 20 + 5 + + 20 + 25 + 15 + 20 = 105 (км.).

Рисунок 4 - Решение задачи о нахождении минимального маршрута доставки
Маршрут из города Суйфэньхе в Хабаровск, при котором время доставки товара будет наименьшим, включает город 3, город 5, город 6, город 7 и город 9.Длина маршрута составит 105 километров.
2.3 Задача коммивояжера
Коммивояжер желает посетить 6 городов. Они соединены сетью дорог
Расстояние между городом 1 и городом 2 составляет 6 км, между городом 1 и городом 3 - 7 км, между городом 1 и городом 4 - 20 км, между городом 1 и городом 5 - 12 км, между городом 1 и городом 6 - 10 км. Расстояние между городом 2 и городом 3 составляет 5 км, между городом 2 и городом 4 - 7 км, между городом 2 и городом 5 - 9 км, между городом 2 и городом 6 - 16 км. Расстояние между городом 3 и городом 4 составляет 4 км, между городом 3 и городом 5 - 10 км, между городом 3 и городом 6 - 12 км. Расстояние между городом 4 и городом 5 составляет 3 км, между городом 4 и городом 6 - 15 км. Расстояние между городом 5 и городом 4 составляет 6 км, между городом 5 и городом 6 - 4 км, между городом 6 и городом 3 - 11 км, между городом 6 и городом 5 - 21 км. Коммивояжёр должен посетить все 6 городов по одному разу, вернувшись в тот, с которого начал. Требуется найти такой маршрут движения, при котором суммарное пройденное расстояние будет минимальным
Данную задачу можно решить венгерским методом, методом совершенного паросочетания. Для этого требуется построить матрицу А, отображающую длину между городами: a>ij> – расстояние от города i до города j (i ≠j), если i = j, то ставится ∞ ,так как дороги не существует.
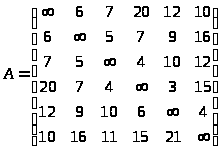
Строится приведенная матрица с целью получения в каждой строке и столбце не меньше одного кратчайшего маршрута (нулевого приведенного значения). Для этого в каждой строке матрицы А от каждого элемента отнимается значение минимального элемента этой строки:

Вычисляется коэффициент приведения, равный сумме всех минимальных элементов матрицы А, которые вычитали из строк и столбцов:
К>пр> = 6 +5 + 4 + 3 + 4 + 10 = 32
Вычисляются коэффициенты значимости для каждого занулившегося элемента, где a>ij> – элементы приведенной матрицы.

К>12> = 1 + 1 = 2
К>23 >= 2
К>34> = 1 + 2 = 3
К>45> = 5 К>61> = 2
К>56> = 2 + 4 = 6
Из приведенной матрицы нужно вычеркнуть строку и столбец, содержащие элемент с максимальным коэффициентом значимости. В данном случае таким элементом является а>56>: коэффициент значимости равен 6. Для элемента а>56> установим значение1: а>56> = 1.

Коэффициент значимости:
К>12> = 2
К>23> = 2
К>45> = 5
К>61> = 2
К>34> = 3
5) а>45> = 1
Коэффициент значимости:

К>12> = 2
К>61> = 2
К>34> = 3
К>23 >= 2
а>45> = 1
Коэффициент значимости:

К>12> = 7
К>61> = 7
К>23 >= 2
а>12 >= 1, а>61> = 1
а>23> = 1
Таким образом, в маршрут вошли ребра: {5,6}, {4,5}, {3,4}, {1,2}, {6,1}, {2,3}. Все вершины (города) соединились. Длина маршрута составляет w({5,6}) + w({4,5}) + w({3,4}) +w({1,2}) + w({2,3}) = 4 + 3 + 4 + 6 + 10 + 5 = 32. Путь коммивояжера включает расстояния между городами {1,2},{2,3},{3,4},{4,5},{5,6},{6,1}, и имеет длину 32.
3. Практическое применение теории нечетких множеств
Под конкурентоспособностью понимают комплекс потребительских, стоимостных и социальных характеристик товара (изделия), определяющих его успех на данном рынке, т. е. способность данного товара быть обмененным на деньги на конкретном рынке в условиях широкого предложения к обмену других товаров-аналогов. Конкурентоспособность — это степень соответствия совокупности свойств объекта ценностной системе рынка. Границы понятия конкурентоспособность непрерывно расширяются, переходя от конкурентоспособности изделия к конкурентоспособности предприятий и даже государств. Конкурентоспособность обеспечивается высоким технологическим уровнем и качеством, соответствием требованиям и стандартам стран-импортеров, фирм-покупателей, высоким уровнем технологического обслуживания, патентной чистотой и патентной защитой, приемлемой ценой, льготными условиями платежа и т. д. Фирме, занимающейся реализацией компьютеров, необходимо из шести предложенных марок ноутбуков ASUS L8400, ASUS T9, FUJITSU – SIEMENS LIFEBOOK B, IRU NOVIA 1012DVD, COMPAQ EVO N610C, INTEL JS2310 выбрать модель с оптимальным набором характеристик (дисплей с большим количеством точек, процессор с высокой тактовой частотой, большой объем оперативной памяти, жесткий диск с большим объемом памяти, долгий срок автономной работы, маленький вес, низкая стоимость, большой гарантийный срок ). Известно, что ноутбук ASUS L8400 обладает следующими качествами: дисплей 14.5 точек, процессор 1 ГГц, память 256 Мбайт, жесткий диск 20 Гбайт, привод DVD-ROM, время автономной работы 2,7 часа, вес 2.9 кг, цена 1.5 тыс. долларов США, гарантийный срок 3 года. Ноутбук ASUS T9 обладает следующими качествами: дисплей 14.1 точек, процессор 0.8 ГГц, память 128 Мбайт, жесткий диск 15 Гбайт, привод DVD-ROM, время автономной работы 2.5 часа, вес 2.1кг, цена 1.16 тыс. долларов США, гарантийный срок 2 года. Ноутбук FUJITSU–SIEMENS LIFEBOOK B: дисплей 10.4 точек, процессор 0.7 ГГц, память 256 Мбайт, жесткий диск 30 Гбайт, привод CD-RW, время автономной работы 2.4 часа, вес 1.6кг, цена 2 тыс. долларов США, гарантийный срок 2.5 года. Ноутбук IRU NOVIA 1012DVD: дисплей 12.0 точек, процессор 1.06 ГГц, память 128 Мбайт, жесткий диск 20 Гбайт, привод DVD-CDRW, время автономной работы 2.5 часа, вес 1.7 кг, цена 1.48 тыс. долларов США, гарантийный срок 1 год. Ноутбук COMPAQ EVO N610C: дисплей 14.0 точек, процессор 1.6 ГГц, память 256 Мбайт, жесткий диск 40 Гбайт, привод DVD-CDRW, время автономной работы 2.4 часа, вес 2.1 кг, цена 2 тыс. долларов США, гарантийный срок 3 года. Ноутбук INTEL JS2310: дисплей 14.0 точек, процессор 1.12 ГГц, память 256 Мбайт, жесткий диск 25 Гбайт, привод CD-RW, время автономной работы 2.5 часа, вес 1.9 кг, цена 1.37 тыс. долларов США, гарантийный срок 1 год. Данная задача может быть решена с помощью метода нечеткого отношения предпочтения /3/. Задачу выбора определенной марки ноутбука с учетом наиболее важных критериев качества рассмотрим на примере анализа альтернатив: a>1> – ASUS L8400, a>2 >– ASUS T9, a>3> – FUJITSU–SIEMENS LIFEBOOK B, a>4> – IRU NOVIA 1012DVD, a>5> - COMPAQ EVO N610C, a>6> – INTEL JS2310. Для оценки альтернатив используем девять критериев качества, где, на основе данных об основных характеристиках ноутбуков задаются множества значений, которые могут принимать различные характеристики: F>1>- дисплей (от 10 до 15 тыс. точек.), интерес представляет дисплей с большим количеством точек; F>2>- процессор (от 0,6 до 1,7 ГГц), предпочтение отдается процессору с большей тактовой частотой; F>3>- память (от 120 до 300 Мбайт), интерес представляет ноутбук с большим объемом памяти; F>4>- жесткий диск (от 10 до 45 Гбайт), предпочтение отдается жесткому диску с большим объемом памяти; F>5>- привод (от 1 до 10 баллов), предпочтение составляет большее количество баллов; F>6>- время автономной работы (от 2 до 3,5 часов), предпочтительнее большее количество часов автономной работы; F>7>- вес (от 1 до 3 кг), интерес составляет ноутбук с меньшим весом; F>8>- стоимость (от 1 до 3 тыс. долларов США), предпочтение отдается ноутбуку с меньшей ценой;
F>9>- срок гарантии (от 0,5 до 3,5 лет), предпочтение отдается ноутбуку с большим гарантийным сроком.
Теперь на основании функций принадлежности всех альтернатив находятся их значения по девяти критериям /6/. Для функции принадлежности утверждения «величина х мала» рассчитывается по формуле:

1, 0 < х < а>1>
=
 ,
а>1>≤ х ≤ а>2
>(12)
,
а>1>≤ х ≤ а>2
>(12)
0, х> а>2>
Для функции принадлежности утверждения «величина х большая» рассчитывается по формуле:
0 , 0
< х < а>1>
, 0
< х < а>1>
=
 ,
а>1>≤ х ≤а>2
>(13)
,
а>1>≤ х ≤а>2
>(13)
1, х > а>2>
Для F>1> значение F>1> рассчитывается по следующей формуле
0 , 0
< х < 10
, 0
< х < 10
F>1>=
 ,
10 ≤х ≤ 15
,
10 ≤х ≤ 15
1, х > 15
μ>F>>1>={0.9/ а>1>; 0.8/ а>2>; 0.1/ а>3>; 0.4/ а>4>; 0.7/ а>5>; 0.7/ а>6>}

a>3>
a>4>
a>5>>,> a>6>
a>2>
a>1>
Рисунок 5– График функции принадлежности для F1
Для F>2> значение F>2> рассчитывается по следующей формуле
0 ,
0< х < 0,7
,
0< х < 0,7
F>2>=
 ,
0,6 ≤ х ≤ 1,7
,
0,6 ≤ х ≤ 1,7
1, х > 1,7
μ>F>>2>={0.6/ а>1>; 0.4/ а>2>; 0.3/ а>3>; 0.7/ а>4>; 0.9/ а>5>; 0.8/ а>6>}

a>3>
a>2>
a>1>
a>4>
a>6>
a>5>
Рисунок 6 - График функции принадлежности для F2
Для F>2> значение F>3> рассчитывается по следующей формуле
0 , 0
< х < 120
, 0
< х < 120
F>3>=
 ,
120 ≤ х ≤ 300
,
120 ≤ х ≤ 300
1, х > 300
μ>F>>3>={0.8/ а>1>; 0.4/ а>2>; 0.8/ а>3>; 0.4/ а>4>; 0.8/ а>5>; 0.8/ а>6>}

а>1>,а>3>,
а>5,>а>6>
a>2,>
a>4>
Рисунок 7 - График функции принадлежности для F3
Для F>4> значение F>4> рассчитывается по следующей формуле
0 , 0
< х < 10
, 0
< х < 10
F>4>=
 ,
10 ≤ х ≤ 45
,
10 ≤ х ≤ 45
1, х > 45
μ>F>>4>={0.3/ а>1>; 0.1/ а>2>; 0.6/ а>3>; 0.3/ а>4>; 0.9/ а>5>; 0.4/ а>6>}

a>3>
a>5>
a>3>
а>1>
а>4>
a>2>
Рисунок 8 - График функции принадлежности для F4
Для F>5> значение F>5> рассчитывается по следующей формуле

0, 0 < х < 1
F>5>=
 ,
1 ≤ х ≤ 10
,
1 ≤ х ≤ 10
1, х > 10
μ>F>>5>={0.5/ а>1>; 0.6/ а>2>; 0.3/ а>3>; 0.8/ а>4>; 0.8/ а>5>; 0.3/ а>6>}

Р
а>1>
а>4>
исунок 9 - График функции принадлежности для F5Для F>6> значение F>6> рассчитывается по следующей формуле
0 , 0
< х < 2
, 0
< х < 2
F>6>=
 ,
2 ≤ х ≤ 3.5
,
2 ≤ х ≤ 3.5
1, х > 3.5
μ>F>>6>={0.7/ а>1>; 0.3/ а>2>; 0.2/ а>3>; 0.3/ а>4>; 0.2/ а>5>; 0.3/ а>6>}

Рисунок 10 - График функции принадлежности для F6
Для F>7> значение F>7> рассчитывается по следующей формуле
1 ,
0 < х < 1
,
0 < х < 1
F>7>=
 ,
1 ≤ х ≤3
,
1 ≤ х ≤3
0, х > 3
μ>F>>7>={0.3/ а>1>; 0.5/ а>2>; 0.7/ а>3>; 0.8/ а>4>; 0.5/ а>5>;0.6/ а>6>}

а>1>
а>2>
а>5>
а>6>
а>3>
а>4>
Рисунок 11 - График функции принадлежности для F7
Для F>8> значение F>8> рассчитывается по следующей формуле
1 ,
0 < х < 1
,
0 < х < 1
F>8>=
 ,
1 ≤ х ≤ 3
,
1 ≤ х ≤ 3
0, х > 3
μ>F>>8>={0.6/ а>1>; 0.9/ а>2>; 0.5/ а>3>; 0.8/ а>4>; 0.5/ а>5>; 0.7/ а>6>}

Рисунок 12 - График функции принадлежности для F8
Для F>9> значение F>9> рассчитывается по следующей формуле
0 , 0
< х < 0.5
, 0
< х < 0.5
F>9>=
 ,
0.5 ≤ х ≤3,5
,
0.5 ≤ х ≤3,5
1, х > 3,5
μ>F>>9>={0.9/ а>1>; 0.6/ а>2>; 0.8/ а>3>; 0.4/ а>4>; 0.9/ а>5>; 0.4/ а>6>}

а>2>
а>1>
а>5>
а>4>
а>6>
а>3>
Рисунок 13 - График функции принадлежности для F9
На основе графиков функций принадлежности всех альтернатив по девяти критериям определены их конкретные значения.
По этим данным составим матрицы нечётких отношений предпочтения R1 ,…,R9, причём элементы этих матриц находятся по формуле (14):
 (14)
(14)
>R>>1
> >R>>2
>
>R>>2
>
>R>>3
> >R>>4
>
>R>>4
>
>R>>5
> >R>>6
>
>R>>6
>
>R>>7
> >R>>8
>
>R>>8
>
>R>>9
>
Задача выбора решается в соответствии с описанной выше процедурой, строится нечеткое отношение Q>1> = R>1> R>2 > … R>9>:
Q>1>=
Находится множество недоминируемых
альтернатив на множестве {A,
μ>Q>>1>}:
получаем множество
 НД=║1,1,1,1,1,1║
НД=║1,1,1,1,1,1║
Строится отношение Q>2>:
Коэффициенты w>k> относительной важности критериев по оценке автора работы имеют следующие значения:
W>1>=0,1; W>2>=0,15; W>3>=0,1; W>4>=0,15; W>5>=0,09; W>6>=0,1; W>7>=0,05; W>8>=0,2; W>9>=0,06.
Определяется нечёткое отношение Q>2>:
 (15)
(15)
>Q2>(a1,a2)= 0,1*0,1 + 0,15*0,2 + 0,1*0,4 + 0,15*0,2 + 0,09*0 + 0,1*0,2 + +0,05*0 + 0,2*0 + 0,06*0,2 = 0,142.
Аналогично вычисляем остальные элементы матрицы.
Q>2>=
Находится подмножество
недоминируемых альтернатив множества
{А,
 }:
}:
 (16)
(16)
по всем i и j (ij),Находится подмножество недоминируемых альтернатив множества {A, μ>Q>>2>}:
μ>Q>>2>н,д,(а>1>)=1- max{0; 0,162 – 0,079; 0,219 – 0,065;0,16 – 0,107; 0,09 – 0,172; 0,108 – 0,08}= 0,846
μ>Q>>2>н,д,(а>2>)=1- max{0,079 – 0,162; 0; 0,22 – 0,131; 0,078 – 0,108; 0,1 – 0,265; 0,068 – 0,15}= 0,911,
μ>Q>>2>н,д,(а>3>)=1- max{0,065 - 0,219; 0,131 – 0,22;0; 0,104 – 0,21; 0,01 – 0,246; 0,059 – 0,145}= 1
μ>Q>>2>н,д,(а>4>)=1- max{0,107 - 0,16; 0,108 – 0,078; 0,21 – 0,109;0;0,085 – 0,22; 0,075 – 0,08}= 0,899
μ>Q>>2>н,д,(а>5>)=1- max{0,172 – 0,09; 0,265 – 0,1; 0,246 – 0,01; 0,22 – 0,085; 0 ; 0,165 – 0,055}= 0,764
μ>Q>>2>н,д,(а>6>)=1- max{0,08 – 0,108; 0,15 – 0,068; 0,145 – 0,059; 0,08 – 0,075; 0,055 - – 0,165; 0 }= 0,914
В результате получается: μ>Q>>2>н,д,(>i>)=(0,846 0,911 1 0,899 0,764 0,914)
Результирующее множество недоминируемых альтернатив есть пересечение множеств μ>Q>>1>н,д, и μ>Q>>2>н,д,:
μ>Q>>1>н,д, μ>Q>>2>н,д,={(1 1 1 1 1 1) (0,846 0,911 1 0,899 0,764 0,914)}= =(0,846 0,911 1 0,899 0,764 0,914)
Следовательно, рациональным следует считать выбор альтернативы >3>, имеющей максимальную степень недоминируемости, равную 1.
Таким образом, с учетом всех перечисленных критериев и их относительной важности, наилучшим для фирмы, занимающейся реализацией компьютеров, будет выбор ноутбука модели FUJITSU–SIEMENS LIFEBOOK B.
Заключение
В данной курсовой работе были рассмотрены такие разделы дискретной математики как применение математической логики, теории графов и элементов теории нечётких множеств. Было рассмотрено на конкретных примерах, как алгоритмы дискретной математики применяются в сфере экономики, в частности, при решении проблемы выбора из нескольких альтернатив.
В первой части курсовой работы было рассмотрено применение методов дискретной математики и математического моделирования в экономике и математической логике, где рассматриваются логические операции и преобразование логических функций, приведение функций к дизъюнктивной и конъюнктивной нормальной форме, построение таблицы истинности, нахождение полинома Жегалкина для заданной функции и её производных по одной и двум переменным.
Во второй части на конкретных примерах рассматривается практическое применение теории графов в экономике. Были решены экономические задачи с использованием таких алгоритмов, как «жадный» (алгоритм Краскала) и алгоритма Дейкстры. Составлены математические модели данных алгоритмов. С помощью венгерского метода, было получено решение для задачи коммивояжера.
В третьей части решена задача, целью которой является выбор оптимальной альтернативы, из шести предложенных. Решение было получено посредством многокритериального выбора альтернатив на основе нечёткого отношения предпочтения. Данный способ весьма удобен для решения различных экономических задач. Для расчетов, в третьей части, использовался табличный редактор «Excel», в целях экономии времени, затрачиваемого на вычисления, а также для наибольшей точности расчетов.
Список использованных источников
Яблонский С.В. Введение в дискретную математику: Учеб. пособие / Под ред. В.А. Садовничего. – 3-е изд.; стер. – М.: Высшая школа, 2001. – 384 с.
Новиков Ф.А. Дискретная математика для программистов. СПб., Питер, 2002. 304 с.
Матюхина Л.Я. Математическое моделирование в экономике: методические указания к курсовой работе. Хабаровск, 2002. 20 с.
Белоусов А.И, Ткачев С.Б. Дискретная математика. М., Издательство МГТУ имени Н.Э. Баумана, 2003, 631 с.
Гаврилов С.П. Сапоженко А.А. Сборник задач по дискретной математике. – М.: Наука, 1978
Галкина В.А. Дискретная математика: комбинаторные методы оптимизации. М., Наука, 2003, 232с.
Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. М., Высшая школа, 2004, 128 с.
Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.
Свами М.Н., Тхуласираман К. Графы, сети и алгоритмы: Пер. с англ. – М.: Мир, 1984. – 455 с.
 >
>

 >
> >
> >
>
 >
>
