Нарисна геометрія
Нарисна геометрія
Вступ
Засновником «Нарисної геометрії» є видатний французький геометр кінця VXIII – початку XIX століття Гаспар Монж. У своєму класичному творі «Geometry descriptive» (Нарисна геометрія), який був опублікований у 1798 р., Г. Монж розробив загальну геометричну теорію, яка надає можливість на плоскому аркуші, який містить ортогональні проекції тривимірного тіла, вирішувати різні стереометричні задачі. Винайдений ним метод, метод ортогонального проеціювання на дві взаємно перпендикулярні площини проекцій, до цього часу залишається єдиним способом створення креслення.
Предметом «Нарисна геометрія» є викладення та обґрунтування методів побудови зображень просторових фігур на площини проекцій та розв’язання задач геометричного характеру за побудованими зображеннями. Нарисна геометрія є кращим засобом розвитку в людини просторового уявлення, без якого неможлива інженерна діяльність. Нарисна геометрія є теоретичною базою для складання креслення. Креслення – це своєрідна мова, за допомогою якої можна отримати зображення геометричних фігур на площини проекцій, застосовуючи лише точки, прямі та обмежений набір геометричних індексів, букв та цифр. Мова ця інтернаціональна, оскільки зрозуміла будь – якому інженеру, незалежно від того, на якій мові він розмовляє та в якій точці Земної кулі він живе.
1. Проекції точки
Будь-яку геометричну фігуру розглядають як множину точок, які їй належать. Тому проекції геометричної фігури на площини проекцій отримують шляхом проеціювання належних їй точок на площини проекцій.
Усі побудови, які виконуються у нарисній геометрії, базуються на методі проеціювання. Залежно від апарату проеціювання проекції поділяють на центральні та паралельні (рис. 1.1).
Центральною проекцією точки називають точку перетину променя, проведеного через задану точку простору (А, В), та центр проекцій S з площиною проекцій (П>1>). (рис. 1.1 а).
Центральне проеціювання найчастіше застосовують у архітектурі, в машинобудуванні застосовується паралельне проеціювання.

а) б)
Рисунок 1.1 – Методи проеціювання: а) центральне; б) паралельне
Залежно від напрямку проеціювання паралельне проеціювання поділяють на косокутне (напрямок проеціювання не перпендикулярний площині проекцій) та прямокутне (напрямок проеціювання перпендикулярний площині проекцій). Прямокутне проеціювання найчастіше називають ортогональним. Ортогональною проекцією точки називають точку перетину променя, проведеного через точку простору перпендикулярно площині проекцій, з площиною проекцій.
Як для центрального, так і для паралельного проеціювання справедливе твердження, що будь-якій точці простору відповідає одна єдина центральна (або паралельна) її проекція. Але при такому апараті проеціювання по центральній (або паралельній) проекції точки однозначно неможливо встановити її положення у просторі. Необхідно мати якусь допоміжну умову. Такою допоміжною умовою є проеціювання на дві площини проекцій.
1.1 Проекції точки на дві взаємно перпендикулярні площини проекцій
Щоб отримати ортогональні проекції точки на дві взаємно перпендикулярні площини проекцій, необхідно з точки простору (точка А) послідовно провести перпендикуляри до перетину їх з горизонтальною та фронтальною площинами проекцій (рис. 1.2).На рисунку 1.2 використані такі позначення: П>1> – горизонтальна площина проекцій; П>2 >– фронтальна площина проекцій; О – початок координат; Х, У, Z – осі координат; А – точка у просторі; А>1> та А>2> – відповідно горизонтальна та фронтальна проекції точки.
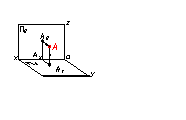
Рисунок 1.2 – Проекції точки на дві площини проекцій
Для побудови комплексного креслення або епюра Монжа (рис. 1.3) необхідно площину П>2 >залишити без змін, а площину П>1> розвернути на 900 вниз до суміщення з площиною П>2>. Послідовно виміряти та відкласти на відповідних осях абсцису, ординату та аплікату точки (рис. 1.3).

Рисунок 1.3 – Побудова епюра Монжа
1.2 Проекції точки на три взаємно перпендикулярні площини проекцій
Щоб отримати ортогональні проекції точки на три взаємно перпендикулярні площини проекцій, необхідно через точку простору послідовно провести перпендикуляри на горизонтальну, фронтальну та профільну площини проекцій (рис. 1.4). У перетині проведених перпендикулярів з кожною з площин проекцій одержують ортогональні проекції точки А: горизонтальну (А>1>), фронтальну (А>2>) та профільну (А>3>) проекції точок.

Рисунок 1.4 – Проекції точки на три площини проекцій
На рисунку 1.4 використані такі позначення: П>1>, П>2>, П>3> – відповідно горизонтальна, фронтальна та профільна площини проекцій; О – початок координат; Х, У, Z – осі координат; А – точка у просторі; А>1>, А>2>, А>3> – проекції точки А відповідно на П>1>, П>2>, П>3>.
Для побудови комплексного креслення (епюр Монжа) необхідно площину П>2 >залишити без змін, площину П>1> розвернути на 900 вниз, а площину П>3> розвернути на 900 на право до суміщення з площиною П>2> (рис. 1.5). Послідовно виміряти та відкласти на відповідних осях абсцису, ординату та аплікату точки А.

Рисунок 1.5 – Епюр Монжа
1.3 Основні властивості ортогонального проеціювання
Положення точки у просторі визначається трьома її координатами (X, Y, Z).
Горизонтальна проекція точки визначається її абсцисою (Х) та ординатою (У), фронтальна проекція точки – її абсцисою (Х) та аплікатою (Z), профільна проекція точки – її ординатою (У) та аплікатою (Z).
Наслідки:
Віддалення точки від площин проекцій визначається відповідними координатами:
координатою Х – від площини П>3>;
координатою У – від площини П>2>;
координатою Z – від площини П>1>.
Однойменні проекції точок знаходяться на одній лінії проеційного зв’язку, перпендикулярній до відповідної осі.
Положення точки у просторі визначається двома її проекціями, тому за двома проекціями точки завжди можна побудувати її третю проекцію.
Приклад 1 За двома проекціями точки А визначити її третю проекцію.

а) б) в)
Рисунок 1.6 – Побудова третьої проекції точки
За умовами задачі дані дві проекції точки: фронтальна та профільна (рис. 1.6а). Для побудови горизонтальної проекції точки А необхідно з фронтальної проекції точки провести лінію проеційного зв’язку, перпендикулярну до осі Х (рис. 1.6б), на якій відкласти ординату точки (рис. 1.6в), яка виміряється на профільній площині проекцій (відстань позначено двома штрихами).
Аналогічно можна побудувати фронтальну проекцію точки за її горизонтальною та профільною проекціями або профільну проекцію точки за горизонтальною та фронтальною проекціями.
2. Проекції прямої
Положення прямої у просторі визначається положенням двох точок, які їй належать. Тому для побудови комплексного креслення прямої достатньо мати проекції двох точок, які їй належать (рис. 1.7).
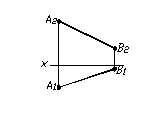
Рисунок 1.7 – Проекції прямої лінії
2.1 Положення прямої відносно площин проекцій
Залежно від положення прямої відносно площин проекцій прямі поділяють на прямі загального положення та особливого положення.
Прямими загального положення називають прям, не паралельні жодній з площин проекцій (рис. 1.7).
Прямі особливого положення поділяють на прямі рівня та прямі проеціювальні.
Прямі рівня – це прямі, які паралельні одній з площин проекцій. Залежно від того, якій площині проекцій пряма паралельна, їх поділяють на прямі горизонтального, фронтального та профільного рівня. На рисунку 1.8 наведені приклади прямих рівня: АВ – фронтальна пряма рівня, CD – горизонтальна пряма рівня, EF – профільна пряма рівня.

Рисунок 1.8 – Прямі рівня
Прямі проеціювальні (рис. 1.9) – це прямі, які паралельні одночасно двом площинам проекцій, тобто перпендикулярні до третьої, на яку вони проектуються у вигляді точки. Залежно від того, до якої площини проекцій прямі перпендикулярні, їх називають горизонтально-проеціювальними (відрізок EF), фронтально-проеціювальними (відрізок CD) та профільно-проеціювальними (відрізок AB).

Рисунок 1.9 – Прямі проеціювальні
Комплексне креслення (епюр Монжа) проеціювальних прямих наведене на рисунку 1.10.

Рисунок 1.10 – Комплексне креслення проеціювальних прямих
2.2 Визначення натуральної величини відрізка способом прямокутного трикутника
Аналізуючи
положення відрізків прямої відносно
площин проекцій, можна зробити висновок,
що лише у тому випадку, коли відрізок
прямої займає особливе положення, на
комплексному кресленні маємо натуральну
величину відрізка. Для прямих загального
положення на площини проекцій відрізок
прямої проектується із спотворенням.
При розв’язанні багатьох задач нарисної
геометрії досить часто виникає
необхідність мати натуральні величини
відрізків прямих ліній. Натуральну
величину відрізка, який займає загальне
положення, можна визначити способом
прямокутного трикутника (рис. 1.11).
Суть способу полягає в тому, що
натуральну величину відрізка (НВ)
визначають як гіпотенузу прямокутного
трикутника, у якого один катет – це
проекція відрізка на площину проекцій,
а другий – різниця відстаней кінців
відрізка від цієї площини проекцій.
Цей спосіб
проілюстрований на рисунку 1.11, де:
АВ – відрізок у просторі; А>1>В>1>
– горизонтальна проекція відрізка;
 Z
– різниця відстаней кінців відрізка
АВ від горизонтальної площини проекцій;
– кут нахилу відрізка АВ до горизонтальної
площини проекцій.
Z
– різниця відстаней кінців відрізка
АВ від горизонтальної площини проекцій;
– кут нахилу відрізка АВ до горизонтальної
площини проекцій.

Рисунок 1.11 – Визначення натуральної величини відрізка
На рисунку 1.12 (а та б) наведений приклад визначення натуральної величини відрізків та кутів нахилу їх до відповідних площин проекцій.

а) б)
Рисунок 1.12 – Визначення натуральної величини відрізка та кутів нахилу його до площин проекцій
3. Проекції площини
Існують шість способів завдання площини у просторі: трьома точками, які не належать одній прямій, прямою та точкою, яка не належить цій прямій, двома паралельними прямими, двома прямими, які перетинаються, геометричною фігурою (відтинання площини), слідами площини.
3.1 Способи завдання площини на комплексному кресленні
На комплексному кресленні площина може бути задана:
проекціями трьох точок, які не належать одній прямій (рис. 1.13);
проекціями прямої та точки, яка не належить цій прямій (рис. 1.14);

Рисунок 1.13 Рисунок 1.14
проекціями двох паралельних прямих (рис. 1.15);
проекціями двох прямих, які перетинаються (рис. 1.16);

Рисунок 1.15 Рисунок 1.16
проекціями відтинання площини (рис. 1.17);
слідами площини (рис. 1.18).
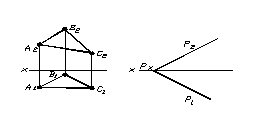
Рисунок 1.17 Рисунок 1.18
3.2 Положення площини відносно площини проекцій
Залежно від положення заданих площин відносно площин проекцій їх поділяють на площини загального положення та площини особливого положення.
Площинами загального положення називають площини, які не перпендикулярні до жодної з площин проекцій. Приклади площин загального положення наведені на рисунках 1.13 – 1.18.
Площини особливого положення поділяють на площини проеціювальні та площини рівня.
Якщо задана площина перпендикулярна до однієї з площин проекцій, то вона на неї проектується у вигляді відрізка. Такі площини називаються проеціювальними. Залежно від того, якій площині проекцій задані площини перпендикулярні, їх називають горизонтально – проеціювальними (рис. 1.19а), фронтально – проеціювальними (рис. 1.19б) та профільно-проеціювальними (рис. 1.19в).


а) б) в)
Рисунок 1.19 – Площини проеціювальні
Площини рівня – це площини, які перпендикулярні одночасно до двох площин проекцій, тобто паралельні третій площині проекцій, на яку вони проектуються у натуральну величину.
Залежно від того, якій площині проекцій задана площина паралельна, площини називають площинами горизонтального рівня (рис. 1.20а), фронтального рівня (рис. 1.20б) та профільного рівня (рис. 1.20в).



а) б) в)
Рисунок 1.20 – Площини рівня
3.3 Належність точки та прямої площині
1 Пряма належить площині, якщо вона проходить через дві точки, які їй належать (рис. 1.21а).
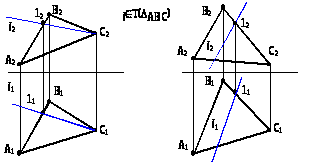
а) б)
Рисунок 1.21 – Належність прямої площині
2 Пряма належить площині, якщо вона проходить через точку, яка належить цій площині та паралельна прямій, яка знаходиться у площині (рис. 1.21б).
Точка належить площині, якщо вона знаходиться на прямій, належній площині. На рисунку 1.22а точка 1 належить площині трикутника АВС, оскільки точка належить стороні АВ трикутника АВС. На рисунку 1.22б точка 2 не належить площині трикутника АВС.

а) б)
Рисунок 1.22 – Належність точки прямій
3.4 Головні лінії площини
До прямих, які займають особливе положення, відносять горизонталі, фронталі, профільні прямі та прямі найбільшого нахилу до площин проекцій.
Горизонталями площини (h) називають прямі, які належать площині та паралельні горизонтальній площині проекцій. На рисунках 1.23а (площина задана прямою та точкою, яка не належить цій площині) та 1.23б (площина задана слідами) наведені приклади побудови горизонталей площин.
Побудову горизонталі починають з її фронтальної проекції (h>2>), оскільки вона паралельна осі Х>12.> Горизонтальну проекцію (h>1>) визначають по лініях проеційного зв’язку.

а) б)
Рисунок 1.23 – Побудова горизонталі площини
Фронталями площини (f) називають прямі, які належать площині та паралельні фронтальній площині проекцій. На рисунку 1.24а та б наведені приклади проведення фронталей площин, які задані різними способами.
Побудову фронталі починають з її горизонтальної проекції (f>1>), оскільки вона паралельна осі Х>12>, її фронтальну проекцію (f>2>) визначають по лініях проеційного зв’язку.
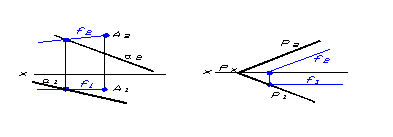
а) б)
Рисунок 1.24 – Побудова фронталі площини
Профільними прямими називають прямі, які належать площині та паралельні профільній площині проекцій.
Лініями найбільшого нахилу до площини проекцій називають прямі, які належать заданій площині та паралельні горизонталі, фронталі або профільній прямій. Лінії найбільшого нахилу до площин проекцій дають можливість визначати кути нахилу до відповідних площин проекцій.
4. Перетворення комплексного креслення
Аналізуючи положення прямих та площин стосовно площин проекцій зрозуміло що, лише у тому випадку, коли вони займають особливе положення (рисунки 1.8, 1.10, 1.20), на одній (або двох) площині проекцій матимемо натуральну величину. Якщо прямі чи площини займають загальне положення, натуральної величини бути не може. Для визначення натуральної величини розмірів площини чи відрізка існує кілька способів: заміна площин проекцій, обертання навколо проеціювальної осі, обертання навколо прямої рівня, плоскопаралельне переміщення.
Щоб визначити натуральну величину геометричного об’єкта, необхідно або змінити систему площин проекцій так, щоб об’єкт зайняв особливе положення, або розвернути сам об’єкт у просторі так, щоб він зайняв особливе положення стосовно існуючої системи площин проекцій.
4.1 Спосіб заміни площин проекцій
Суть способу полягає в тому, що положення геометричного об’єкта у просторі залишається незмінним, а одну з площин проекцій замінюють новою, яка створює з другою площиною проекцій нову систему взаємно перпендикулярних площин, відносно якої геометричний об’єкт займе особливе положення. Замін може бути декілька. Способом заміни площин можна розв’язувати багато позиційних та метричних задач нарисної геометрії.
Приклад 2 Визначити натуральну величину відрізка АВ.

Рисунок 1.25 – Визначення натуральної величини відрізка способом заміни площин проекцій
Для визначення натуральної величини відрізка необхідно ввести допоміжну площину проекцій П>4>, яка перпендикулярна до горизонтальної площини проекцій та паралельна відрізку АВ.
Площина П>4 >вводиться на будь – якій відстані від відрізка АВ. На комплексному кресленні достатньо провести нову вісь Х>14> паралельно горизонтальній проекції відрізка АВ та з А>1 >та В>1 >провести лінії зв’язку, перпендикулярні до осі Х>14, >на яких відкласти віддалення від горизонтальної площини проекцій, які вимірюються на площині П>2> (зроблені позначки однією та двома рисками). На рисунку 1.25 позначений кут нахилу (a) прямої АВ до горизонтальної площини проекцій – це буде кут між НВ прямої АВ та прямою паралельною осі Х>14>.
Щоб визначити кут нахилу прямої АВ до фронтальної площини проекцій, необхідно ввести площину, перпендикулярну до площини П>2> та паралельну відрізку АВ.
Приклад 3 Визначити натуральну величину трикутника АВС (рис. 1.26).

Рисунок 1.26 – Визначення натуральної величини трикутника способом заміни площин проекцій
Для розв’язання задачі двічі виконують заміну площин проекцій.
Перша заміна виконана таким чином, щоб трикутник перетворити у проеціювальну площину. Для цього необхідно нову вісь Х>14> провести перпендикулярно до горизонтальної проекції горизонталі (h>1>) – це ознака того, що трикутник перпендикулярний до нової площини проекцій (П>4>), на яку він проектується у відрізок.
Друга заміна виконана таким чином, щоб трикутник перетворити у площину рівня. Для досягнення цього необхідно нову вісь Х>45> провести паралельно відрізку, в який спроектувався трикутник АВС.
Відстані, які необхідно виміряти та відкласти від нових осей, позначені відповідними лініями.
4.2 Спосіб обертання навколо проеціювальної осі
Суть способу полягає в тому, що система площин проекцій залишається незмінною, а геометричний елемент змінює своє положення у просторі, займаючи особливе положення відносно площин проекцій. Усі точки геометричного об’єкта обертаються у площинах, паралельних тій площині проекцій, відносно якої вісь обертання перпендикулярна. Якщо вісь обертання перпендикулярна до горизонтальної площини проекцій, то на комплексному кресленні всі горизонтальні проекції точок геометричного об’єкта пересуваються по
колах, а фронтальні проекції – по прямих, паралельних осі Х.
Приклад 4 Визначити натуральну величину трикутника АВС (рис. 1.27).

Рисунок 1.27 – Визначення натуральної величини трикутника способом обертання навколо проеціювальної осі
Для визначення натуральної величини трикутника АВС необхідно провести горизонталь площини.
Першим обертанням трикутник переведено у проеціювальне положення. Обертання виконано навколо прямої, проведеної через точку А, перпендикулярної до площини П>1>.
Друге обертання виконано навколо прямої, проведеної через точку В, перпендикулярно до площини П>2>. Трикутник переведений у положення паралельності площині П>1>, тому горизонтальна проекція трикутника – це його натуральна величина.
Основним недоліком способу обертання навколо проеціювальної осі є накладання одного зображення на інше. При розв’язанні задач способом плоскопаралельного переміщення цього недоліку немає.
4.3 Спосіб плоскопаралельного перенесення
Суть способу полягає в тому, що система площин залишається незмінною, а геометричний об’єкт займає особливе положення відносно площин проекцій, що дає можливість розв’язувати позиційні та метричні задачі. Цей спосіб вважають винятковим способом обертання навколо проеціювальної осі. На комплексному кресленні одна з проекцій геометричного об’єкта, не змінюючи своїх розмірів, змінює своє положення відносно осі Х>12>. Тоді всі точки другої проекції пересуваються по прямих, паралельних осі Х>12>.
Приклад 5 Визначити натуральну величину відрізка АВ.

Рисунок 1.28 – Визначення натуральної величини відрізка способом плоско паралельного переміщення
У даному прикладі для визначення натуральної величини відрізка способом плоскопаралельного переміщення горизонтальну проекцію відрізка (А>1 >В>1>) розміщують на вільному місці креслення паралельно осі Х>12>. Фронтальна проекція відрізка АВ буде його натуральною величиною. Для її побудови необхідно з фронтальних проекцій точок А>2> та В>2> провести лінії, паралельні осі Х>12> до перетину з лініями проекційного зв’язку, проведених від горизонтальних проекцій цих точок.
Приклад 6 Визначити натуральну величину трикутника АВС.
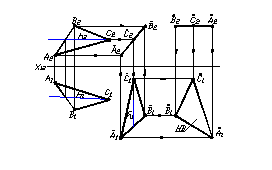
Рисунок 1.29 – Визначення натуральної величини трикутника способом плоскопаралельного переміщення
Щоб визначити натуральну величину трикутника АВС, необхідно спочатку перетворити площину загального положення в площину проеціювальну (у наведеному прикладі – фронтально – проеціювальну), а потім у площину рівня (на рисунку 1.29 – це площина горизонтального рівня). Для виконання таких перетворень перш за все необхідно провести горизонталь площини трикутника.
Щоб перетворити площину загального положення у площину фронтально проеціювальну, необхідно горизонтальну проекцію трикутника розмістити так, щоб горизонталь його стала перпендикулярна до осі Х. У цьому разі всі фронтальні проекції вершин трикутника будуть пересуватися паралельно осі Х до перетину з лініями зв’язку, проведеними з горизонтальних проекцій вершин трикутника АВС. На фронтальну площину проекцій трикутник проектується у вигляді відрізка прямої лінії.
Щоб перетворити площину фронтально-проеціювальну у площину горизонтального рівня, необхідно фронтальну проекцію трикутника (відрізок прямої) розмістити паралельно осі Х – тоді горизонтальні проекції вершин трикутника будуть пересуватися паралельно осі Х до перетину з відповідними лініями зв’язку. Горизонтальна проекція трикутника – це натуральна величина його.
5. Поверхні
Світ поверхонь багатогранний та різноманітний. Із усього різноманіття найбільш поширеними є багатогранники та поверхні обертання.
Багатогранниками називають поверхні, які обмежені площинами (гранями). До багатогранників відносять призми та піраміди (рис. 1.30).

Рисунок 1.30 – Багатогранники
Залежно від того, яка геометрична фігура є основою багатогранника, їх називають тригранними, чотиригранними, п’ятигранними призмами чи пірамідами.
Поверхні обертання утворені обертанням твірної (прямої або кривої лінії) навколо нерухомої осі. До поверхонь обертання відносять конус, циліндр, сферу, тор. На рисунку 1.31 наведені комплексні креслення конуса, циліндра, сфери та тора.

Рисунок 1.31 – Поверхні обертання
5.1 Точки на поверхнях
Для побудови проекції точки, яка належить поверхні, за заданою проекцією необхідно перш за все з’ясувати, якому елементу поверхні точка належить.
Якщо точка належить поверхні призми чи піраміди, то для побудови другої проекції точки достатньо провести лінії проекційного зв’язку. При побудові проекцій точок, які належать будь-якій поверхні, необхідно пам’ятати про видимість. Невидимі проекції точок позначають у дужках, наприклад, (А>1>) – горизонтальна проекція точки А невидима.
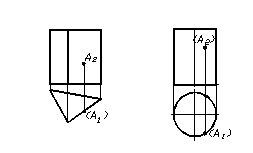
Рисунок 1.32 – Точки на поверхнях
На рисунку 1.32 наведені приклади побудови горизонтальних проекцій точок, які належать поверхням піраміди та циліндра. Задані фронтальні проекції точок. Для побудови горизонтальних проекцій точок необхідно провести лінії зв’язку на відповідні елементи поверхонь з урахуванням видимості. У наведених прикладах для поверхні призми фронтальна проекція точки А видна, її горизонтальна проекція – невидна. На поверхні циліндра – фронтальна та горизонтальні проекції точки А не видні.
Для визначення точок, які належать поверхням піраміди або конуса, необхідно виконати допоміжні побудови.
Якщо точка належить ребру піраміди, то для побудови другої проекції точки необхідно провести лінію зв’язку на відповідне ребро. У наведеному на рисунку 1.33а прикладі шукана точка D знаходиться на ребрі SC. За умовами задачі задана фронтальна проекція точки D. Для побудови її горизонтальної проекції достатньо провести лінію зв’язку на горизонтальну проекцію ребра SC.


а) б)
Рисунок 1.33 – Точки на поверхні піраміди
Якщо точка належить грані піраміди, то через задану точку у відповідній грані необхідно провести допоміжну пряму.
У наведеному прикладі задана фронтальна проекція точки R. Точка R належить грані SAC. Для побудови її горизонтальної проекції послідовно виконують такі дії:
через задану точку на грані SAC провести фронтальну проекцію допоміжної прямої SD;
побудувати горизонтальну проекцію допоміжної прямої (S>1>D>1>);
по лінії проеційного зв’язку визначити горизонтальну проекцію точки R на грані ASC.
5.2 Перетин поверхонь проеціювальними площинами
Якщо будь-яку геометричну поверхню перетнути проеціювальною площиною, то одна з проекцій лінії перетину очевидна – це відрізок прямої лінії, який збігається з проекцією проеціювальної площини. Другу проекцію лінії перетину будують за точками, які їй належать.
Якщо проеціювальна площина перетинає поверхню призми або циліндра, ніякі побудови не виконуються, а лише позначаються проекції лінії перетину. На рисунку 1.34 наведені приклади побудови проекцій лінії перетину призми та циліндра фронтально-проеціювальними площинами та визначена натуральна величина перерізів способом заміни площин проекцій (для призми) та способом плоскопаралельного переміщення (для циліндра).

а) б)
Рисунок 1.34 – Перетин призми та циліндра фронтально-проеціювальними площинами
Горизонтальна проекція фігури перерізу піраміди фронтально-проеціювальною площиною наведена на рисунку 1.35 Для її побудови проведені лінії проеційного зв’язку на відповідні ребра піраміди. Натуральна величина фігури перетину визначена способом плоскопаралельного переміщення.
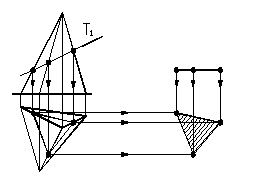
Рисунок 1.35 – Перетин піраміди фронтально-проеціювальною площиною
Фігура перерізу конуса фронтально-проеціювальною площиною залежить від положення січної площини відносно елементів конуса. На рисунку 1.36 наведені приклади побудови перерізів конуса фронтально-проеціювальними площинами.

Рисунок 1.36 – Переріз конуса проеціювальними площинами
При виконанні контурів машинобудівних креслень можливі варіанти, коли необхідно побудувати перетин складного тіла проеціювальною площиною (рис. 1.37а) та визначити натуральну величину перерізу. Пропоноване на рисунку 1.37а тіло складається із послідовно встановлених одну на одну шестигранної призми, циліндра та тригранної піраміди.


а) б)
Рисунок 1.37 – Переріз складного тіла фронтально-проеціювальною площиною
Для розв’язання цієї задачі необхідно перш за все побудувати профільну проекцію пропонованого тіла (рис. 1.37б) – вигляд зліва.
Переріз піраміди фронтально-проеціювальною площиною – чотирикутник 1234. Фронтальна проекція його – це відрізок, обмежений точками 1>2>≡2>2> та 3>2>≡4>2>, який визначається без зайвих побудов. Горизонтальну та профільну проекції чотирикутника одержують по лініях проеційного зв’язку, визначаючи точки на відповідних елементах піраміди: точки 1 та 2 належать ребрам, а 3 та 4 – основі піраміди. На рисунку 1.38а, б та в наведена поетапна побудова фігури перерізу піраміди заданою площиною.


а) б)

в)
Рисунок 1.38 – Побудова проекцій перерізу піраміди фронтально-проеціювальною площиною
Переріз циліндра даною площиною – еліпс, зрізаний з двох сторін прямими лініями, обмежений точками 5 – 10. Фронтальна проекція фігури перерізу (рис. 1.39) – відрізок, обмежений точками 5>2> ≡ 6>2> та 9>2 >≡ 10>2>. Горизонтальні проекції точок 5 – 10 знаходять по лініях проеційного зв’язку на горизонтальній проекції циліндра (коло). Профільні проекції точок 5 – 10 визначають по лініях проеційного зв’язку (рис. 1.39), проведених із точок 5>2>≡6>2>, 7>2>≡8>2> та 9>2>≡10>2>. Відстань точок від осі симетрії виміряють на горизонтальній площині та відкладають на відповідній ліній проеційного зв’язку. Шукані профільні проекції точок, належних фігурі перерізу, послідовно з’єднують плавною кривою лінією.

Рисунок 1.39 – Побудова проекцій перерізу циліндра фронтально-проеціювальною площиною
Фігура перерізу шестигранної призми заданою фронтально-проеціювальною площиною – чотирикутник, обмежений точками 11, 13, 14 та 12.
Фронтальна проекція фігури перерізу – це пряма лінія, яка обмежена точками 11>2> ≡ 12>2> та 13>2> ≡ 14>2> (рис. 1.40).
Горизонтальні проекції точок 11, 12, 13 та 14 визначені по лініях проекційного зв’язку в перетині з контуром горизонтальної проекції шестигранної призми (рис. 1.40).

Рисунок. 1.40 – Побудова проекцій фігури перерізу призми фронтально-проеціювальною площиною
Профільні проекції точок 11, 12, 13 та 14 одержують по лініях проеційного зв’язку на відповідних ребрах шестигранної призми (рис. 1.40). Так, точки 11 та 12 належать верхній основі призми, а точки 13 та 14 – бічним ребрам. Для визначення профільних проекцій точок 13 та 14 достатньо з фронтальних проекцій цих точок провести лінії зв’язку до перетину з відповідними ребрами. Для визначення положення профільних проекцій точок 11 та 12 необхідно з фронтальної проекції їх (точка 11>2> ≡ 12>2>) провести лінії зв’язку, на яких відкласти відстані, які виміряються на горизонтальній площині проекцій (на рисунку 1.40 це відстані від горизонтальної осі симетрії поверхні вниз та вверх відповідно до точок 13>1> та 14>1>).
Натуральну величину фігури перерізу пропонованої деталі заданою фронтально-проеціювальною площиною найпростіше визначити способом плоскопаралельного переміщення (рис. 1.41). Для цього фронтальну проекцію фігури перерізу – пряму лінію разом з точками 1>2> – 14>2>, які їй належать, розмістити на вільному місці креслення паралельно осі х. Горизонтальні проекції нового положення точок 1 –14 одержують в перетині ліній проеційного зв’язку, які проведені з нового положення фронтальної проекції фігури перерізу, з прямими, які проведені паралельно осі, з горизонтальних проекцій точок 1 – 14 (рис. 1.41).

Рисунок 1.41 – Визначення натуральної величини фігури перерізу поверхні фронтально-проеціювальною площиною
6. Побудова розгорток
У різних галузях техніки та будівництва при виготовленні виробів з листового матеріалу часто мають справу з розгортками поверхонь.
Одержують ці розгортки за допомогою послідовного суміщення елементів поверхні з площиною.
6.1 Побудова розгортки піраміди
Щоб побудувати розгортку тригранної піраміди, необхідно перш за все визначити натуральні величини ребер піраміди одним із способів перетворення комплексного креслення. Найпростіше це виконати способом плоскопаралельного переміщення. Для цього на вільному місці креслення розмістити, наприклад, горизонтальні проекції бічних ребер так, щоб вони стали паралельні осі Х. Зважаючи на те, що кожне ребро має спільну точку – вершину S, зручніше накладати одне ребро на інше (рис. 1.42). Натуральну величину ребер одержують на фронтальній площині проекцій у перетині ліній проеційного зв’язку, які проведені з кінців кожного ребра, з лініями, які проведені паралельно осі з кінців фронтальних проекцій ребер (рис. 1.42).
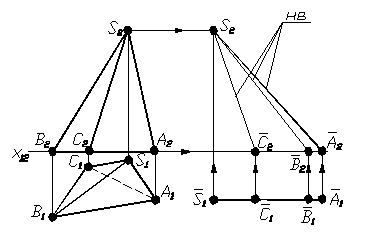
Рисунок 1.42 – Визначення натуральної величини ребер піраміди
Розгортку піраміди будують способом тріангуляції. Для цього з довільно вибраної точки S провести промінь, на якому відкласти натуральну величину будь-якого ребра (рис. 1.43а), наприклад, SA (натуральну величину виміряють на фронтальній площині проекцій).
Для побудови грані, наприклад ASB, необхідно визначити положення точки В за двома заданими А та S (рис. 1.43б)). Точку В визначають у перетині дуг, які проведені із точок А та S та дорівнюють натуральним величинам відповідно до сторони основи АВ (виміряються на горизонтальній площині проекцій, оскільки основа паралельна горизонтальній площині проекцій) та бічного ребра ВS, натуральна величина якого визначена на фронтальній площині проекцій.

а) б)
Рисунок 1.43 – Побудова грані SAB способом тріангуляції
Інші дві грані (SBC таSCA) бічної поверхні піраміди будують так само, як грань ASB (рис. 1.44).

Рисунок 1.44 – Розгортка бічної поверхні піраміди
Для завершення побудови повної розгортки піраміди необхідно до будь-якої грані, наприклад до грані ASB, добудувати трикутник основи (рис. 1.45).
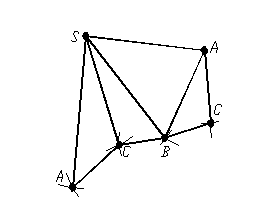
Рисунок 1.45 – Повна розгортка піраміди
6.2 Розгортка призми
Розгортка поверхні призми складається із розгортки бічної поверхні – це прямокутники, кількість яких залежить від форми основи призми, та двох основ (рис. 1.46).

Рисунок 1.46 – Розгортка призми
Кожний прямокутник має розміри сторін: висота призми, натуральна величина якої виміряється на фронтальній площині проекцій та відповідну сторону основи, натуральна величина якої виміряється на горизонтальній площині проекцій.
6.3 Розгортка циліндра
Розгортка циліндра складається з бічної поверхні, яка є прямокутником, одна сторона якого дорівнює висоті циліндра, а інша – довжині кола основи циліндра (2πR), та двох основ циліндра – кола радіусом R (рис. 1.47).

Рисунок 1.47 – Розгортка циліндра
При виконанні розгортки циліндра її поверхню апроксимують призмою. Для цього коло основи поділяють на кілька рівних частин (наприклад, на вісім). Тоді при побудові прямокутника бічної поверхні на горизонтальній прямій відкладають хорду кола стільки разів, на скільки частин поділене коло (рис. 1.48).
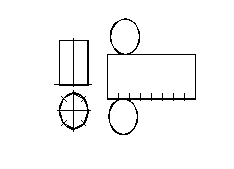
Рисунок 1.48 – Побудова розгортки циліндра
6.4 Розгортка конуса
Розгортка конуса складається з бічної поверхні, що є сектором кола, радіус якого дорівнює твірній, а кут визначається за формулою α = 3600R/l, та основи конуса.
При побудові розгортки конуса її поверхню найчастіше апроксимують поверхнею піраміди. Для цього основу поділяють на кілька рівних частин (на рисунку 1.49а – на вісім).
Прямий конус має однакові твірні, натуральною величиною яких є твірні, що обмежують фронтальну проекцію конуса (рис. 1.49а).
Нахилений конус має різні твірні. Натуральну величину мають твірні, що обмежують фронтальну проекцію конуса. Натуральну величину всіх інших твірних визначають способом обертання навколо проеціювальної осі (рис. 1.49б).

а) б)
Рисунок 1.49 – Визначення натуральних величин твірних конуса
Бічну поверхню розгортки нахиленого конуса будують способом тріангуляції.
6.5 Розгортка бічної поверхні складної поверхні
Доволі часто у інженерній практиці виникає необхідність будувати розгортки бічних поверхонь, що мають переходи від прямокутного контуру до кола та навпаки. На рисунку 1.50 зліва наведене креслення такого переходу, а справа – наочне зображення його.

Рисунок 1.50 – Зображення складної поверхні
Бічна поверхня пропонованого переходу складається із послідовно розміщених гранних поверхонь та поверхонь конуса. Поверхня симетрична, тому досить виконати половину розгортки бічної поверхні.
Для побудови половини трикутної грані (трикутника 123) необхідно на вільному місці креслення провести вертикальну лінію, на якій відкласти натуральну величину сторони трикутника, наприклад, 12 (фронтальна проекція відрізка 2>2>1>2> – натуральна величина). З точки 1 вправо відкласти під прямим кутом до 12 натуральну величину половини основи трикутника (натуральна величина відстані 13 виміряється на горизонтальній площині проекцій). Натуральні величини позначені на кресленні та розгортці відповідно однією та двома лініями. З’єднавши точки 1, 2 та 3, дістаємо половину трикутної грані (рис. 1.51) пропонованої поверхні.
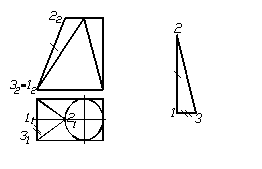
Рисунок 1.51 – Побудова елемента розгортки
Далі за трикутною гранню йде частина нахиленого конуса з вершиною у точці 3, першою твірною якого є сторона 23 трикутної грані.
Щоб побудувати розгортку конічної поверхні, необхідно розбити частину кола між точками 2 та А (основа конуса) на кілька частин (на рисунку 1.52 на три частини). Натуральна величина твірних 3С та 3В визначається способом обертання навколо проеціювальної осі, яка проходить через точку 3. Натуральна величина твірної 3А – це її фронтальна проекція. Розгортку конічної поверхні будують способом тріангуляції (рис. 1.52).
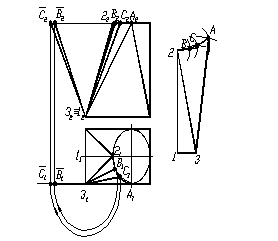
Рисунок 1.52 – Побудова розгортки конічної поверхні
Далі до розгортки необхідно додати трикутну грань 3А4, яка проектується у натуральну величину на фронтальну площину проекцій (рис. 1.53).


Рисунок 1.53 – Побудова розгортки гранної поверхні
Потім до розгортки додається конічна поверхня з вершиною у точці 4 (рис. 1.54).

Рисунок 1. 54 – Побудова розгортки конічної поверхні
Завершує побудову розгортки бічної поверхні половина трикутної грані 4F5, яка у натуральну величину проектується на профільну площину проекцій. На рисунку 1.55 наведена половина розгортки бічної поверхні пропонованої на рисунку 1.50 деталі.

Рисунок 1.56 – Розгортка складної поверхні
7. Аксонометрія
Аксонометрією називають зображення предмета разом з координатною системою, до якої він віднесений, на вибрану аксонометричну площину проекцій (рис. 1.56).
Залежно від напрямку проеціювання аксонометрію поділяють на косокутну та прямокутну.
Косокутною називають аксонометрію, коли напрямок проеціювання не перпендикулярний до заданої площини проекцій. Прямокутною називають аксонометрію, коли напрямок проеціювання перпендикулярний до заданої площини проекцій.

Рисунок 1.56 – Побудова аксонометричної проекції точки А
ГОСТ 2.317–68 встановлює п’ять типів аксонометричних проекцій: прямокутна ізометрія (рис. 1. 57а), прямокутна диметрія (рис. 1.57б), косокутна фронтальна ізометрія (рис. 1.57в), горизонтальна ізометрія (рис. 1.57 г.), фронтальна диметрія (рис. 1.57д).

Рисунок 1.57 – Типи аксонометричних проекцій
Найчастіше виконують прямокутну ізометрію деталей. Координатні осі ізометрії розміщені під кутом 1200, поетапна побудова яких наведена на рисунку 1.58.

Рисунок 1.58 – Поетапна побудова ізометричних осей
Для побудови ізометричної проекції точки досить виміряти на комплексному кресленні та послідовно відкласти на відповідних аксонометричних осях абсцису, ординату та аплікату заданої точки (рис. 1.59).

Рисунок 1.59 – Ізометрична проекція точки А
Ізометрія кола – це еліпс, велика та мала осі якого орієнтуються по-різному залежно від того, якій площині він належить або якій паралельний (рис. 1.60).

Рисунок 1.60 – Ізометрія кола
При побудові ізометрії кола слід пам’ятати про те, що велика вісь еліпса завжди перпендикулярна до відсутньої у даній площині осі, а мала вісь з нею збігається. При цьому, велика вісь еліпса дорівнює 1,22D, а мала – 0,71D.
Щоб виконати ізометрію деталі, пропонованої на рисунку 1.50, необхідно виконати контур нижньої основи – це прямокутник, а потім визначити положення верхньої основи – це коло, яке проектується у вигляді еліпса (рис. 1.61).
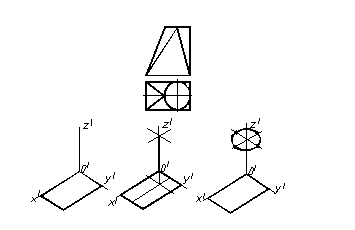
Рисунок 1.61 – Побудова ізометричних проекцій основ складної поверхні
На завершальному етапі побудови аксонометричної проекції пропонованої деталі необхідно з’єднати точки верхньої та нижньої основи – одержуємо ізометрію бічної поверхні (рис. 1.62а)). Потім необхідно видалити лінії невидимого контуру (рис. 1.632б).

а) б)
Рисунок 1.62 – Ізометрична проекція складної поверхні