Теория вероятности и математическая статистика (работа 3)
Московский авиационный институт
(технический университет)
Курсовая работа
Дисциплина: Теория вероятности и математическая статистика
Выполнил
студент группы Р 2/1
Истелюев Батырбек.
Ахтубинск-2004
Задания
Проверить выполнение теоремы Бернулли на примере электрической схемы.
Методом дискретных случайных величин смоделировать случайную величину, имеющую закон распределения Пуассона. Заполнить массив из 300 точек.
Критерием Колмогорова проверить, что данный массив имеет соответствующий закон распределения.
Краткая теория
В теории вероятности часто встречается такой характер приближения одних величин к другим, и для его описания введен специальный термин: «сходимость по вероятности».
Говорят, что величина X>n> сходится по вероятности к величине а, если при сколь угодно малом е вероятность неравенства │X>n>–a│<e с увеличением неограниченно приближается к единице. Применяя этот термин, можно сказать, что при увеличении числа опытов частота события не стремится к вероятности события, а сходится к ней по вероятности. Это свойство составляет содержание теоремы Бернулли.
Например, при бросании монеты 10 раз теоретически возможно, что все 10 раз появится герб, т.е частота появлений будет равна 1; при 1000 бросаниях такое событие возможно, но приобретает меньшую вероятность; при еще большом количестве бросаний вероятность становится на столько мала, что это событие можно считать практически неосуществимым.
Теорема Я. Бернулли: при увеличении количества опытов, частота появлений событий сходится по вероятности к вероятности этого события.
Теорема Я. Бернулли утверждает устойчивость частоты при постоянных условиях опыта. Но при изменяющихся условиях опыта аналогичная устойчивость также существует. Теорема, устанавливающая свойство устойчивости частот при переменных условиях опыта, называется теоремой Пуассона.
Закон Пуассона.
Рассмотрим случайную величину Х, которая может принимать целые, неотрицательные значения: 0,1,2,…,m,…
Говорят, что эта СВ Х распределена по закону Пуассона, если вероятность того, что она примет определенное значение m, выражается формулой:
P>m>=(am/m!)*e-a (m=0,1,2…), a – некоторая положительная величина называемая параметром закона Пуассона.
Ряд распределения СВ Х, распределенный по закону Пуассона, имеет вид:
-
xm
0
1
2
…
m
…
pm
e-a
(a/1!)*e-a
(a2/2!)*e-a
…
(am/m!)*e-a
…
Математическое ожидание данного распределения случайной величины равно параметру закона Пуассона а: m>x>=a; Дисперсия также равна этому параметру: D>x>=a. Таким образом дисперсия случайной величины, распределенной по закону Пуассона равна ее математическому ожиданию и равна параметру а.
Это свойство применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина Х, распределена по закону Пуассона, для этого определяют из опыта статистические характеристики: математическое ожидание и дисперсию. Если их значения близки, то гипотеза является правдоподобной.
Дискетной называется случайная величина, возможные значения которой есть отдельные изолированные числа (т.е. между двумя возможными соседними значениями нет возможных значений), которые эта величина принимает с определенными вероятностями. Другими словами, возможные значения дискретной случайной величины можно перенумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (в последнем случае множество всех возможных значений называют счетным).
Законом распределения называют перечень ее возможных значений и соответствующих им вероятностей.
Критерий А.Н. Колмогорова.
В качестве меры расхождения между теоретическим и статистическим распределениями Колмогоров рассматривает максимальное значение модуля разности между статистической функцией распределения F* (x) и соответствующей теоретической функцией распределения F(x) :
D=max│F*(x)–F(x)│.
Основанием для выбора в качестве расхождения величины D является простота ее вычисления. Вместе с тем она имеет достаточно простой закон распределения. Колмогоров доказал, что, какова бы ни была функция распределения F(x) непрерывной случайной величины X, при неограниченном возрастании числа независимых наблюдений n вероятность неравенства
D√n≥ λ стремится к пределу P(λ)=1–∑>k>>=-∞>∞(-1)k e-2∙k^(2)∙λ^(2) значения Р(λ) можно найти по таблице, зная λ.
Задание №1
Проверить выполнение теоремы Бернулли на примере электрической схемы:
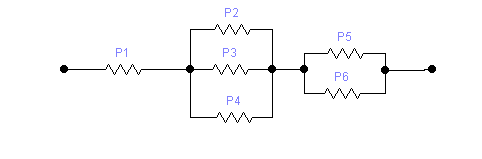
Пусть вероятность того, что каждый элемент данной схемы не выйдет из строя, равна:
Р>1>=0,6; Р>2>=0,4; Р>3>=0,5; Р>4>=0,7; Р>5>=0,3; Р>6>=0,8.
Программа, полученная в среде PASCAL:
Program Shema;
Uses CRT;
Var a:array[1..6] of integer;
p,x:array[1..6] of real;
m,n,i,j,c:integer;
R,S,B:real;
BEGIN
CLRSCR;
p[1]:=0.6;p[2]:=0.4;p[3]:=0.5;p[4]:=0.7;p[5]:=0.3;p[6]:=0.8;
n:=1000;
c:=0;
while n<=25000 do begin
m:=0;
for i:=1 to n do begin
for j:=1 to 6 do begin
x[j]:=random;
if x[j]<p[j] then a[j]:=1 else a[j]:=0;
end;
if a[1]*(a[2]+a[3]+a[4])*(a[5]+a[6])>=1 then m:=m+1;
end;
R:=m/n;
writeln('кол-во опытов=',n:5,' P=',R:5:3);
S:=S+R;
n:=n+1000;
inc(c);
end;
S:=S/c;
writeln;
writeln('Вероятность безотказной работы=', s:4:5);
writeln;
B:=p[1]*(1-(1-p[2])*(1-p[3])*(1-p[4]))*(1-(1-p[5])*(1-p[6]));
writeln('Вероятность работы(2-ой способ) =' , B:4:5);
readln;
END.
Результаты работы:
кол-во опытов= 1000 P=0.476
кол-во опытов= 2000 P=0.480
кол-во опытов= 3000 P=0.474
кол-во опытов= 4000 P=0.463
кол-во опытов= 5000 P=0.476
кол-во опытов= 6000 P=0.470
кол-во опытов= 7000 P=0.467
кол-во опытов= 8000 P=0.463
кол-во опытов= 9000 P=0.473
кол-во опытов=10000 P=0.476
кол-во опытов=11000 P=0.468
кол-во опытов=12000 P=0.466
кол-во опытов=13000 P=0.462
кол-во опытов=14000 P=0.472
кол-во опытов=15000 P=0.473
кол-во опытов=16000 P=0.464
кол-во опытов=17000 P=0.469
кол-во опытов=18000 P=0.474
кол-во опытов=19000 P=0.471
кол-во опытов=20000 P=0.472
кол-во опытов=21000 P=0.467
кол-во опытов=22000 P=0.464
кол-во опытов=23000 P=0.468
кол-во опытов=24000 P=0.466
кол-во опытов=25000 P=0.469
Вероятность безотказной работы=0.46972
Вероятность работы(2-ой способ) =0.46956
Вывод: по результатам видно, что вероятность безотказной работы цепи, при большом количестве опытов, сходится к общей вероятности безотказной работы этой цепи, значит, частота событий при большом числе опытов приближается к вероятности этого события, о чем говорит теорема Бернулли.
Задание №2
Смоделировать массив из 300 дискретных случайных величин, имеющий закон распределения Пуассона.
Программа:
Program Puasson;
Uses CRT;
Const a=5; d=15; n=300;k=d+1;
Var i,j,w:word;sums,ran:real;
xmin,xmax,mx,Dx,Rx,Sx,Ex,Sk,h:real;
s,al:array[0..d] of real;
x:array[1..n] of byte;
function Pwr(x,p:real):real;
Begin
randomize;
if x>0 then pwr:=exp(p*ln(x))
else pwr:=0;
end;
function fact(x:word):real;
var i:word;
f:real;
Begin
f:=1
if x>0 then for i:=1 to x do f:=f*i;
fact:=f;
end;
Function f(m:word):real;
begin
if m>=0 then f:=pwr(a,m)*exp(-a)/fact(m)
else f:=0;
end;
begin
sums:=0;
for i:=1 to d do begin
s[i]:=f(i);sums:=sums+s[i];
end;
for i:=0 to d do begin al[i]:=0;
for j:=0 to i do al[i]:=al[i]+s[j]/sums;
end;
for w:=1 to n do begin
ran:=random;
for i:=0 to d do begin
if al[i]>ran then begin
x[w]:=i;break;
end;
end;
end;
writeln;
writeln('Массив,полученный по закону распределения Пуассона:');
writeln;
mx:=0;
for i:=1 to n do begin
write(x[i]:2,' ');
mx:=mx+x[i]/n;
end;
Dx:=0;
Sk:=0;
xmin:=x[1];
xmax:=xmin;
for i:=1 to n do begin
Dx:=Dx+sqr(x[i]-mx)/(n-1);
if xmin>x[i] then xmin:=x[i];
if xmax<x[i] then xmax:=x[i];
end;
SX:=sqrt(Dx);
writeln;
Rx:=d;
h:=Rx/k;
Ex:=-3;
for i:=1 to n do begin
Sk:=Sk+((x[i]-mx)*(x[i]-mx)*(x[i]-mx))/(sqr(dx)*sqr(dx)*sqr(dx));
Ex:=Ex+((x[i]-mx)*(x[i]-mx)*(x[i]-mx)*(x[i]-mx))/(sqr(dx)*sqr(dx)*sqr(dx)*sqr(dx))
end;
writeln('Интервал значений случайной величины:',xmin:0:3,'-',Xmax:0:3);
writeln('математическое ожидание=',mx:0:3);
writeln('Дисперсия=',Dx:0:3);
writeln('Среднее квадротическое отклонение=',Sx:0:3);
writeln('Скошенность=',Sk:0:3);
writeln('Эксцесс=',Ex:0:3);
readln;
END.
Результат работы:
Массив, полученный по закону распределения Пуассона:
2 4 5 3 8 5 5 6 5 4 3 1 6 8 7 2 8 8 7 3
8 4 4 1 5 4 2 4 3 4 1 5 7 4 6 3 3 7 4 7
6 5 4 7 2 7 4 10 5 4 4 7 6 5 4 3 4 5 7 5
2 2 3 11 7 7 6 8 4 5 8 7 9 3 6 5 3 3 6 5
7 6 2 5 1 2 6 6 4 2 13 6 5 5 2 3 9 3 7 7
2 7 6 4 3 4 1 7 6 4 5 4 4 4 5 2 5 4 3 6
3 4 4 5 7 4 4 7 6 3 8 5 7 5 4 3 4 5 6 9
2 4 8 6 8 7 6 3 5 9 2 4 8 1 7 1 4 6 6 7
2 2 3 3 3 4 3 3 1 6 7 4 8 2 3 7 5 5 6 4
6 4 9 10 4 6 4 7 4 7 3 2 3 6 9 3 4 5 6 10
5 10 7 9 5 3 4 7 6 5 7 2 3 7 6 4 5 10 3 6
7 10 3 7 5 5 5 7 7 4 5 2 5 2 9 2 5 8 4 4
5 7 5 6 5 5 4 1 3 5 5 6 9 3 5 3 5 2 13 7
7 5 1 5 3 9 7 5 3 5 5 8 7 4 10 5 5 8 7 8
7 3 4 7 8 4 2 7 7 2 3 4 6 7 4 7 4 5 7 2
Интервал значений случайной величины:1.000-13.000
математическое ожидание=5.093
Дисперсия=4.941
Среднее квадротическое отклонение=2.223
Скошенность=0.104
Эксцесс=-2.934
Задание №3:
Критерием Колмогорова проверить, что данный массив, полученный во втором задание, имеет соответствующий закон распределения.
Статистическая обработка полученного массива.
По полученному массиву построим таблицу:
-
X
0
1
2
3
4
5
6
7
8
9
10
11
12
13
M
0
10
26
39
53
54
33
48
17
10
7
1
0
2
где, M – количество точек.
Таблица статистических вероятностей:
-
X
0
1
2
3
4
5
6
7
8
9
10
11
12
13
P(x)
0
0,033
0,0867
0,13
0,1767
0,18
0,11
0,16
0,0567
0,0333
0,2333
0,0033
0
0,0067
Таблица статистических значений функции:
|
X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
F(x) |
0 |
0,033 |
0,12 |
0,25 |
0,4267 |
0,6067 |
0,7167 |
0,8767 |
0,933 |
0,9667 |
0,99 |
0,9933 |
0,9933 |
1 |
Теоретическая обработка
Таблица теоретических вероятностей:
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
P*(x) |
0,00674 |
0,034 |
0,084 |
0,14 |
0,175 |
0,175 |
0,146 |
0,104 |
0,065 |
0,036 |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
0,018 |
0,00824 |
0,00343 |
0,00132 |
4,7*10^(-4) |
1,57*10^(-4) |
4,92*10^(-5) |
1,46*10^(-5) |
4*10^(-6) |
1,05*10^(-6) |
2,64*10^(-7) |
F(X)=P(X<x), значит таблица теоретических значений функции распределения выглядит так:
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
F*(x) |
0,00674 |
0,04 |
0,125 |
0,265 |
0,44 |
0,616 |
0,762 |
0,867 |
0,932 |
0,968 |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
0,986 |
0,995 |
0,998 |
0,999 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Находим максимальный модуль разности между F(x) и F*(x), она равна
D=│F(6)–F*(6)│=│0,7167–0,762│=0,0453.
Найдем λ=D*√n=0,0453*√300=0,78462.
Вероятность P(λ)=1–∑>k>>=-∞>∞(-1)k e-2∙k^(2)∙λ^(2) равна(при λ=0,78462 из табл)=0,544.
Вывод: Значение вероятности не малое, т.е.>критического значения 0.1, значит гипотезу можно считать правдоподобной.