Теория вероятностей и математическая статистика (работа 5)
Министерство высшего образования Украины
Национальный Технический Университет Украины
“Киевский политехнический институт”
Кафедра автоматизированных систем обработки информации и управления
К о н т р о л ь н а я р а б о т а
по дисциплине :
“ Теория вероятностей и математическая статистика”
Вариант № 24
Выполнил студент гр. ЗІС - 91
ІІI курса факультета ФИВТ
Луцько Виктор Степанович
2009г.
Задача 1
Бросаются две игральные кости. Определить вероятность того, что:
а) сумма числа очков не превосходит N;
б) произведение числа очков не превосходит N;
в) произведение числа очков делится на N.
Исходные данные: N=18.
Решение задачи:
Вероятностью случайного события А называется отношение числа равновозможных элементарных событий, благоприятствующих этому событию, к числу всех равновозможных элементарных событий пространства Е, определяемого данным испытанием.
|
Р(А) = |
m |
|
n |
где: n – число всех равновозможных элементарных событий, вытекающих из условий данного испытания;
m - число равновозможных событий, которые благоприятствуют событию А.
а) при сумме числа очков (N = 18), не превосходящих N:
n = 36;m = 36
|
Р(А) = |
36 |
= |
1 ; |
||
|
36 |
б) при произведении числа очков, не превосходящих N:
n = 28;m = 36
|
Р(А) = |
28 |
= |
7 |
0,778 ; |
||
|
36 |
9 |
в) при произведении числа очков, делящихся на N:
n = 3;m = 36
|
Р(А) = |
3 |
= |
1 |
0,083 . |
|
|
36 |
12 |
Ответы:
а) Р(А) = 1 ;
б) Р(А) = 7/9 0,778 ;
в) Р(А) = 1/12 0,083.
Задача 2
Имеются изделия четырех
сортов, причем число изделий i-го сорта
равно
=1,
2, 3, 4. Для контроля наудачу берутся т
изделий. Определить вероятность того,
что среди них т>1>
первосортных, т>2>,
т>3> и т>4>
второго, третьего и четвертого сорта
соответственно
.
Исходные данные: n>1 >= 3; n>2 >= 1; n>3 >= 6; n>4 >= 2;m>1 >= 2; m>2 >= 1; m>3 >= 3; m>4 >= 1.
Решение задачи.
Определяем количество способов нужной комбинации:
С = С>n1> m1 x С>n2> m2 x С>n3> m3 x С>n4> m4 = С>3> 2 x С>1> 1 x С>6> 3 x С>2> 1 ;
Определяем количество всех возможных способов:
С = С>n1+n2+n3+n4> m1+m2+m3+m4 = С>12> 7 ;
3) Определяем вероятность Р согласно условия задачи:
Р = |
С>3> 2 x С>1> 1 x С>6> 3 x С>2> 1 |
= |
3 х 1 х |
4 х 5 х 6 |
х 2 |
= |
|
2 х 3 |
||||||
|
С>12> 7 |
8 х 9 х 10 х 11 х 12 |
|||||
|
2 х 3 х 4 х 5 |
|
= |
3 х 5 |
= |
5 |
0,15 |
||
|
9 х 11 |
33 |
Ответ: Р = 5/33 0,15 .
Задача 3
Среди п лотерейных билетов
k выигрышных. Наудачу взяли т билетов.
Определить вероятность того, что среди
них
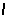выигрышных.
Исходные данные: n = 8; l = 3; m = 5; k = 4.
Решение задачи.
|
k=4 |
|||||||||||||||
|
|
|||||||||||||||
|
n=8 |
|||||||||||||||
Общее число случаев, очевидно, равно С>n> m , число благоприятных случаев С>k> l x С>n-k> m-l , откуда:
|
Р(А) = |
С>k> l x С>n-k> m-l |
= |
С>4> 3 x С>8-4> 5-3 |
= |
3 |
0, 4286 . |
|
С>n> m |
С>8> 5 |
7 |
Ответ: Р(А) = 3/7 0, 4286 .
Задача 7
В круге радиуса R наудачу появляется точка. Определить вероятность того, что она попадает в одну из двух непересекающихся фигур, площади которых равны S>1> и S>2>. Исходные данные:R =14; S>1> = 2,6; S>2> = 5,6.
Решение задачи
|
|
||||||||
|
R S>1> |
||||||||
|
|
P(A) = |
S |
. |
|||||
|
S>2> |
R2 |
|||||||
|
P(A>1>) = |
S>1> |
= |
2,6 |
0,0042246 ; |
||||
|
R2 |
3,14 x 142 |
|
P(A>2>) = |
S>2> |
= |
5,6 |
0,0090991 ; |
||||
|
R2 |
3,14 x 142 |
|
P(A) = |
S>1>+ S>2> |
= |
2,6 + 5,6 |
= |
8,2 |
0,013324 . |
||
|
R2 |
3,14 x 142 |
615,44 |
Ответ: Р(А) 0,013324 .
Задача 8
В двух партиях k>1> и k>2> % доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них:
а) хотя бы одно бракованное;
б) два бракованных;
в) одно доброкачественное и одно бракованное?
Исходные данные: k>1> = 81; k>2> = 37.
Решение задачи
События А и В называются независимыми, если выполняется соотношение:
Р(А/В) = Р(А) / Р(В) .
Для любых событий А и В имеет место формула:
Р(А+В) = Р(А) + Р(В) – Р(АВ) .
Обозначения:
Событие А – выбрали бракованное изделие из 1-й партии (1 – k>1>) ;
Событие B – выбрали бракованное изделие из 2-й партии (1 – k>2>) .
События А и В – независимые.
а) Р(А+В) = Р(А) + Р(В) – Р(АВ) = (1 – k>1>) + (1 – k>2>) – (1 – k>1>)(1 – k>2>) =
= 0,19 + 0,63 – 0,19 х 0,63 0,82 – 0,12 0,70 .
б) Вероятность пересечения двух независимых событий равна произведению вероятностей этих событий:
Р(АВ) = Р(А) х Р(В) = (1 – k>1>)(1 – k>2>) = 0,19 х 0,63 0,12 .
в
)
Р = Р(А) х Р(В) + Р(В) х Р(А) =
(1 – k>1>)k>2>
+ (1 – k>2>)k>1>
=
= 0,19 х 0,37 + 0,63 x 0,81 0,07 + 0,51 0,58 .
Ответы:
а) 0,70;
б) 0,12;
в) 0,58.
Задача 9
Вероятность того, что цель поражена при одном выстреле первым стрелком р>1> вторым — р>2> . Первый сделал n>1>, второй — n>2> выстрелов. Определить вероятность того, что цель не поражена.
Исходные данные: p>1> = 0,33; p>2> = 0,52; n>1> = 3; n>2> = 2.
Решение задачи.
Обозначения:
А – вероятность непоражения цели при одном выстреле первым стрелком (1 – р>1>) ;
В – вероятность непоражения цели при одном выстреле вторым стрелком (1 – р>2>) ;
Р – цель не поражена в результате общего количества испытаний.
Р = (1 – р>1>)n1 x (1 – р>2>)n2 = (1 – 0,33)3 x (1 – 0,52)2 = 0,673 x 0,482 0,30 x 0,23 0,069 0,07 .
Ответ: 0,07 .
Задача 12
Из 1000 ламп n>i>
принадлежат i-й партии, i=1, 2, 3,
.
В первой партии 6%, во второй 5%, в третьей
4% бракованных ламп. Наудачу выбирается
одна лампа. Определить вероятность
того, что выбранная лампа — бракованная.
Исходные данные: n>1> = 350; n>2> = 440.
Решение задачи
Рассмотрим три гипотезы:
Н>1> – выбор лампы из первой партии;
Н>2> – выбор лампы из второй партии;
Н>3> – выбор лампы из третьей партии;
а также событие А – выбор бракованной лампы.
Учитывая то, что Н>1>, Н>2>, Н>3> – полная группа попарно несовместимых событий, причем Р(Нi) 0, i = 1,2,3, то для любого события А имеет место равенство (формула полной вероятности):
|
3 |
||
Р(А) = |
P(H>i>) x P(A/H>i>) . |
|
|
i=1 |
Тогда:
P(H>1>) = 350/1000 = 7/20 ;
P(H>2>) = 440/1000 = 11/25 ;
P(H>3>) = 210/1000 = 21/100 .
Р(А) = 7/20 х 0,06 + 11/25 х 0,05 + 21/100 х 0,04 = 42/2000 + 55/2500 + 84/10000 = 514/10000 = 0,0514 .
Ответ: Р(А) = 0,0514 .
Задача 18
На каждый лотерейный
билет с вероятностью p>1>
может выпасть крупный выигрыш, с
вероятностью р>2>.
— мелкий выигрыш и с вероятностью р>3>
билет может оказаться без выигрыша,
.
Куплено n билетов. Определить вероятность
получения n>1>
крупных выигрышей и n>2>
мелких.
Исходные данные: n = 14; n>1> = 5; n>2> = 4;p>1> = 0,25; p>2> = 0,35.
Решение задачи
Для решения данной задачи используем формулу для полиномиального распределения вероятностей, т.к. события – является ли і-тый билет выигрышным (и насколько) или невыигрышным – независимы (для разных і):
|
P>n>(m>1>,m>2>,…,m>k>) = |
n! |
p>1>m1 p>2>m2 … p>k>mk . |
|
m>1>! m>2>!…m>k>! |
В задаче: А>1> – билет оказался с крупным выигрышем;
А>2> – билет оказался с мелким выигрышем;
А>3> – билет оказался без выигрыша.
|
Р>14>(5,4,5) = |
14! |
х (0,25)5 х (0,35)4 х (0,4)5 = |
6х7х8х9х10х11х12х13х14 |
х |
|
5! 4! 5! |
2х3х4х2х3х4х5 |
х 0,0009765 х 0,015 х 0,01024 = 2 х 7 х 9 х 11 х 13 х 14 х 0,0009765 х 0,015 х
х 0,01024 0,0378.
Ответ: Р 0,0378 .
Задача 19
Вероятность «сбоя» в работе телефонной станции при каждом вызове равна р. Поступило п вызовов. Определить вероятность m «сбоев».
Исходные данные: m = 9; N = 500; p = 0,01.
Решение задачи
q = 1 – p = 1 – 0,01 = 0,99 .
Так как n – большое число (n = N = 500), а npq 5, т.е. npq < 9 , то применяем формулы Пуассона:
|
Р>n>(m) |
am |
e-a , a = np . |
|
m! |
Подсчет вручную дает следующие результаты:
|
Р>n>(m) |
59 |
х |
1 |
|
58 |
х |
1 |
|
|
2х3х4х5х6х7х8х9 |
е5 |
2х3х4х6х7х8х9 |
2,75 |
|
|
390625 |
|
390625 |
0,03751 . |
||
|
72576 х 143,5 |
10 413 862 |
Но, при известных а = 5 и m = 9 результат формулы Пуассона следует брать из таблицы III, где
Р>n>(m) 0,03627 .
Ответ: Р>n>(m) 0,03627 .
Задача 20
Вероятность наступления некоторого события в каждом из n независимых испытаний равна р. Определить вероятность того, что число т наступлений события удовлетворяет следующему неравенству.
Варианты 22—31:
Исходные данные: n = 100; P = 0,3; k>1> = - ; k>2> = 40.
Решение задачи
Вероятность Р>n>(m) того, что в результате этих n опытов событие А произойдет m раз (наступит m успехов), определяется по формуле Бернулли:
P>n>(m) = C>n>mpmqn-m, m = 0,1,2,…,n (1)
где q = 1 – p – вероятность наступления противоположного события А при единичном испытании.
Совокупность чисел, определяемых формулой (1), называется биномиальным распределением вероятностей.
При больших значениях п (порядка десятков, сотен) для биномиального распределения применяют следующие приближенные формулы:
(2)
где:
(3)
где:
(4)
(5)
(6)
Формула (2) основана на локальной теореме Муавра—Лапласа, (3) — на интегральной теореме Муавра—Лапласа, (5) и (6) — на формуле Пуассона. Асимптотику Муавра—Лапласа [формулы (2) и (3)] рекомендуется применять в случае, когда npq>9. В противном случае более точные результаты дает асимптотика Пуассона [формулы (5) и (6)].
З а м е ч а н и е 1. Приближенная формула (3) остается в силе и в том случае, когда входящие в нее неравенства являются строгими.
З а м е ч а н и е 2. Вычисления по формулам (2), (3), (5), (6) выполняются с использованием таблиц I—IV соответственно (см. приложение).
В данной задаче n = 100, т.е. n – число большое.
npq = 21, следовательно npq > 9.
При этом q = 1 – p = 0,7 ;np = 30 .
Наши рассуждения приводят к тому, что данную задачу следует решать с помощью формул Муавра-Лапласа, а именно с помощью формулы (3).
Тогда:
|
k>2> – np |
|
40 – 30 |
|
10 |
2,18 . |
||
|
npq |
4,58 |
4,58 |
|
k>1> – np |
|
0 – 30 |
|
-30 |
- 6,55 . |
||
|
npq |
4,58 |
4,58 |
P>n>(m k>2>) Ф(х>2>) – Ф(х>1>) Ф(2,18) – Ф(- 6,55) Ф(2,18) + Ф(6,55)
0,48537 + 0,5 0,98537 .
Ответ: P>n>(m 40) 0,98537 .
Задача 21
Дана плотность распределения р (х) случайной величины . Найти параметр , математическое ожидание М дисперсию D, функцию распределения случайной величины вероятность выполнения неравенства х>1 >< < х>2>
Варианты 17-24:
Исходные данные: a = -1,5; b = 1; x>1> = -1; x>2> = 1.
Решение.
Р(х) = |
|
, х [-1,5, 1], |
|
0, x [-1,5, 1]. |
Найдем . Должно выполняться соотношение:F>>(+) = 1;
|
p(x)dx = 1; |
dx = 1; |
x |
1 |
= 1; |
*(1+1,5) = 1; |
= |
1 |
=2/5 . |
|
|
-1,5 |
2,5 |
||||||||
|
- |
-1,5 |
|
1 |
|||||||
|
Найдем: М = |
х 2/5 dx = |
2 х2 |
1 |
= |
1/5 (1-2,25) = |
-1,25 |
= -0,25 . |
|
5 2 |
-1,5 |
5 |
|||||
|
-1,5 |
|
1 |
||||
|
Найдем: D = М2 – (М)2 = |
2/5 x2 dx – 0,0625 = 2/5 |
x3 |
1 |
- 0,0625 = |
|
3 |
-1,5 |
|||
|
-1,5 |
= 2/5 (1/3 + 3,375/3) – 0,0625 = 0,4 * 1,4583 – 0,0625 = 0,5833 – 0,0625 = 0,5208 .
|
|
0 , |
x < -1,5; |
||||||
|
x |
x |
|||||||
|
Найдем: F>> (x)= |
p(х) dx = |
dt , |
-1,5 x < 1; |
|||||
|
- |
-1,5 |
|||||||
|
1 , |
x 1 . |
|||||||
|
x |
x |
|||||||
|
dt = |
t |
= |
x + 1,5 = |
2/5x + 0,6 . |
||||
|
-1,5 |
-1,5 |
Найдем: P{-1<<1} = F>> (1) - F>> (-1) = 1 – (-2/5 + 0,6) = 7/5 – 3/5 = 4/5 .
Ответы: 1) = 2/5; 2) М = - 0,25; 3) D = 0,5208; 4) F>> (x) = 0,4x + 0,6; 5) P{-1<<1} = 4/5.
Список использованной литературы
Феллер В. Введение в теорию вероятностей и ее приложения. В 2-х томах. Т.1: Пер.с англ. - М.: Мир, 1994. – 528 с.
Вентцель Е.С. Теория вероятностей: Учеб.для вузов. – 6-е изд.стер. – М.: Высш.шк., 1999. – 576 с.
Сборник задач по теории вероятностей, математической статистике и теории случайных функций. Под редакцией А.А. Свешникова. – М.: Наука, 1998. – 656 с.
Лютикас В.С. Факультативный курс по математике: Теория вероятностей. – М.: Просвещение, 1998. – 160 с.