Теория вероятностей (работа 6)
Содержание
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Список используемой литературы
Задание 1
Найти общее решение дифференциального уравнения первого порядка:
.
Решение:
Преобразуем уравнение и разделяя переменные, получим уравнение с разделенными переменными:
Интегрируем его и получаем общее решение данного уравнения
Ответ: Общее решение данного уравнения
Задание 2
Найти общее решение дифференциального уравнения первого порядка:
.
Решение:
Вводим замену
→
Так как одну
из вспомогательных функций можно взять
произвольно, то выберем в качестве
какой-нибудь частный интеграл уравнения
.
Тогда для отыскания
получим
уравнение
.
Итак, имеем систему двух уравнений:
Далее
Проверка:
верное тождество. Ч. т.д.
Ответ:
Задание 3
Найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям:
,
Решение:
Общее решение данного уравнения
ищется по схеме:
Находим общее
решение
однородного уравнения. Составим
характеристическое уравнение
и
Общее решение имеет вид:
,
где
Находим частное
решение
.
Правая часть уравнения имеет специальный
вид. Ищем решение
,
т.е.
Найдем производные первого и второго порядков этой функции.
|
-2 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
→
→
→
Т.о. частное решение
Общее решение
Используя данные начальных условий, вычислим коэффициенты
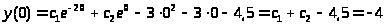
Получим систему двух уравнений:
→
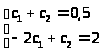
Искомое частное решение:
Ответ:
Задание 4
В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в мягком переплете. Библиотекарь взял 2 учебника. Найти вероятность того, что оба учебника в мягком переплете.
Решение:
Пусть имеется множество N элементов, из которых M элементов обладают некоторым признаком A. Извлекается случайным образом без возвращения n элементов. Вероятность события, что из m элементов обладают признаком А определяется по формуле:
(N=6, M=3, n=2, m=2)
Ответ:
Задание 5
Дана вероятность
появления события A в каждом из
независимых испытаний. Найти вероятность
того, что в этих испытаниях событие A
появится не менее
и
не более
раз.
Решение:
Применим интегральную формулу Муавра-Лапласа
Где
и
Ф (x)
- функция Лапласа
,
обладает свойствами
10.
- нечетная, т.е.
20.
При
,
значения функции представлены таблицей
(табулированы) для
Так
Ответ:
Задание 6
Задан закон распределения дискретной случайной величины X (в первой строке указаны возможные значения величины X, во второй строке даны вероятности p этих значение).
|
X>i> |
8 |
4 |
6 |
5 |
|
p>i> |
0,1 |
0,3 |
0,2 |
0,4 |
Найти:
1) найти
математическое ожидание
,
2) дисперсию
;
3) среднее
квадратичное отклонение
.
Математическое ожидание (ожидаемое среднее значение случайной величины):
Дисперсия (мера рассеяния значений случайной величины Х от среднего значения а):
.
Второй способ вычисления дисперсии:
где
.
Среднее квадратичное отклонение (характеристика рассеяния в единицах признака Х):
→
Ответ:
Математическое
ожидание
Дисперсия
Среднее
квадратичное отклонение
Задание 7
Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно 0,25 мм. Стандартными считаются детали, размер которых заключен между 199,5 мм и 200,5 мм. Найти процент стандартных деталей.
Решение:
Таким образом, процент стандартных деталей составляет 95,45%
Ответ: Стандартных деталей 95,45%.
Список используемой литературы
Горелова Г.В. Теория вероятностей и математическая статистика в примерах и задачах с применением MS Excel. /Под ред. Г.В. Гореловой, И.А. Кацко. - Ростов н/Д: Феникс, 2006. - 475 с.
Ковбаса С.И., Ивановский В.Б. Теория вероятностей и математическая статистика: Учебное пособие для экономистов. - СПб.: Альфа, 2001. - 192 с.
Кочетков Е.С., Смерчинская С.О., Соколов В.В. Теория вероятностей и математическая статистика: Учебник. - М.: ФОРУМ, 2008. - 200 с.
Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник. - М.: ЮНИТИ-ДАНА, 2007. - 551 с.
Пехлецкий И.Д. Математика. / Под ред. И.Д. Пехлецкого. - М.: Издательский центр "Академия", 2003. - 421с.
Пугачев В.С. Теория вероятностей и математическая статистика: Учебное пособие. - М.: ФИЗМАТЛИТ, 2002. - 496 с.