Системы, эквивалентные системам с известным типом точек покоя
Министерство образования Республики Беларусь
Учреждение образования Гомельский государственный
университет имени Франциска Скорины
Математический факультет
Кафедра Дифференциальных уравнений
Курсовая работа
«Системы, эквивалентные системам с известным типом точек покоя»
Гомель 2005
Реферат
Курсовая работа состоит из 14 страниц, 2-х источников.
Ключевые слова: вложимая система, с известным типом точек покоя, первый интеграл дифференциальной системы, отражающая функция, класс систем эквивалентных системе с известным типом точек покоя, непрерывно дифференцируемая функция.
Целью курсовой работы является исследование системы с известным типом точек покоя, нахождение первого интеграла системы, применение теоремы об эквивалентности дифференциальных систем.
Содержание
Введение
Определение вложимой системы. Условия вложимости
Общее решение системы
Нахождение первого интеграла дифференциальной системы и условия его существования
Отражающая функция
Применение теоремы об эквивалентности дифференциальных систем
Заключение
Список использованных источников
Введение
В курсовой работе рассматривается вложимая система с изаестным типом точек покоя. Как известно система является вложимой, если любая компонента этой системы вложима, т.е. система вложима тогда и только тогда, когда множество её решений является подмножеством множества решений некоторой линейной стационарной системы.
В 1–2 м пунктах рассматривается вложимая система, с известным типом точек покоя. Далее проверяем являются ли x и y общим решением нашей системы уравнений.
Во 3-м мы находим первый интеграл системы и проверяем выполнение тождества.
В 4-м пункте применяем теорему об эквивалентности дифференциальных систем.
1. Определение вложимой системы. Условия вложимости
Рассмотрим дифференциальную систему
D.
(1)
Будем называть i-ю
компоненту x
системы (1) вложимой, если для любого
решения x(t)=(x
(t),…,
x
(t)),
t
,
этой системы функция x
t,
является квазимногочленом. Таким образом
i-я
компонента системы (1) вложима тогда и
только тогда, когда для каждого решения
x(t)
этой системы существует линейное
стационарное уравнение вида
,
(2)
для которого
является решением.
Вообще говоря, порядок
и коэффициенты уравнения (2) зависят от
выбора решения
.
В частном случае, когда компонента
любого решения
системы (1) является одновременно и
решением некоторого, общего для всех
решений
уравнения (2), компоненту
системы
(1) будем называть сильно вложимой в
уравнение (2).
2. Общее решение системы
Рассмотрим вложимую систему
(1)
(b>0
и а-постоянные) с общим решением
,
если с
0;
x=0,
y=at+c,
если с=0, где постоянные с, с,
с
связаны соотношением с
(b+c
+c
)=a,
имеет два центра в точках
и
.
Решение:
Подставим общее решение
в нашу систему (1) получим
=
=c(ccosct-csinct)=
a-
Для краткости распишем знаменатель и преобразуем
x+y+b=
=
=a+c(csinct+ccosct)
a-
Получаем, что x и y являются общим решением системы.
3. Нахождение первого интеграла дифференциальной системы и условия его существования
Рассмотрим систему
=
f
(t,
x),
x=
(x,…,
x),
(t,
x)
(1)
с непрерывной в области D
функцией f.
Дифференцируемая функция U
(t,
x),
заданная в некоторой подобласти G
области D,
называется первым
интегралом системы
(1) в области G,
если для любого решения x(t),
t,
системы (1), график которого расположен
в G
функция U
(t,
x(t)),
t,
постоянна, т.е. U
(t,
x(t))
зависит только от выбора решения x(t)
и не зависит от t.
Пусть V
(t,
x),
V:G
R,
есть некоторая функция. Производной от
функции V в
силу системы (1) назовем функцию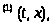 V
V
R,
определяемую
равенством
V
(t,
x(t))
t.
Лемма 1.
Для любого решения
x(t),
t,
системы (1), график которого расположен
в G,
имеет место тождество
V
t.
Без доказательства.
Лемма 2.
Дифференцируемая
функция U
(t,
x),
U:GR,
представляет
собой первый интеграл системы (1) тогда
и только тогда, когда производная U
в силу системы (1) тождественно в G
обращается в нуль.
Необходимость. Пусть U (t, x) есть первый интеграл системы (1). Тогда для любого решения x(t) этой системы, применяя лемму 1 будем иметь тождества
U
Откуда при t=t
получим равенство U(t
справедливое при всех значениях t
и x(t).
Необходимость доказана.
Достаточность.
Пусть
теперь U
при всех (t,
x)
Тогда для любого решения x(t)
системы (1) на основании леммы1
будем иметь тождества
а с ним и достаточность.
Из определения
первого интеграла следует, что постоянная
на G
функция также является первым интегралом
системы (1). Первый интеграл U
(t,
x)
будем называть на G,
если при всех (t,
x)
выполняется неравенство.
Функцию U(x) будем называть стационарным первым интегралом системы (1), если она не зависит от t и является первым интегралом системы (1).
Найдем первый интеграл нашей системы:
Возведем в квадрат и выразим с
y
Положим
,
получим
Проверим, что функция
– это первый интеграл системы (1), т.е.
проверим выполнение тождества
(2)
Найдем производные по t, x, y
После выше сделанных
преобразований получаем, что функция
– это первый интеграл системы (1),
2) Положим
,
т.е.
,
где
,
Q
3) Проверим выполнение тождества:
(3), где
Преобразуем (3).
[в
нашем случае
]
=
=
[учитывая
все сделанные обозначения] =
=
=
=
[ввиду
того, что
которое
в свою очередь как мы уже показали есть
тождественный ноль]
Таким образом, тождество (3) истинное.
4. Отражающая функция
Определение. Рассмотрим систему
(5)
cчитая,
что правая часть которой непрерывна и
имеет непрерывные частные производные
по
.
Общее решение в форме Коши обозначено
через
).
Через
обозначим
интервал существования решения
.
Пусть
Отражающей
функцией
системы (5) назовём дифференцируемую
функцию
,
определяемую формулой
Для отражающей функции справедливы свойства:
для любого решения
системы
(5) верно тождество
для отражающей функции F любой системы выполнены тождества
3) дифференцируемая
функция
будет отражающей функцией системы (5)
тогда и только тогда, когда она
удовлетворяет системе уравнений в
частных производных
и начальному условию
5. Применение теоремы об эквивалентности дифференциальных систем
Получаем
где
-
любая нечетная непрерывная функция.
Наряду с дифференциальной
системой
(1)
рассмотрим возмущенную
систему
(2), где
-
любая непрерывная нечетная функция.
Известно по [3], что дифференциальная
система
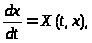
(3)
эквивалентна возмущенной системе
(4), где
непрерывная
скалярная нечетная функция удовлетворяющая
уравнению
Так как выше уже
показано, что функция
где
{есть первый интеграл} удовлетворяет
этому уравнению, то справедлива следующая
теорема.
Теорема1.
Система
(1) эквивалентна системе
(2) в смысле совпадения отражающей
функции.
Так как система
(1) имеет две особые точки, в каждой из
которых находится центр, то и система
(2) имеет центры в этих точках.
Заключение
В данной курсовой работе рассмотрена вложимая система с известным типом точек покоя, проверено удовлетворение общего решения нашей системе, найдены первый интеграл и проверено выполнение тождества, затем с помощью теоремы 1 доказана эквивалентность дифференциальных систем. Сформулированы определения вложимой системы, первого интеграла, отражающей функции и общие свойства отражающей функции. Cформулирована теорема при помощи которой мы доказали эквивалентность нашей системы с дифференциальной системой.
Список использованных источников
Мироненко В.И. Линейная зависимость функций вдоль решений дифференциальных уравнений. – Мн., Изд-во БГУ им. В.И. Ленина, 1981, 50 – 51 с.
Мироненко В.И. Отражающая функция и периодические решения дифференциальных уравнений. – Мн.: изд-во «Университетское», 1986, 11,17 – 19 с.
Мироненко В.В. Возмущения дифференциальных систем, не изменяющие временных симметрий. 2004 г.