Сингулярные интегралы
Федеральное агентство по образованию
Государственное муниципальное образовательное учреждение
высшего профессионального образования
Вятский государственный гуманитарный университет
(ВятГГУ)
Математический факультет
Кафедра математического анализа и методики преподавания математики
Выпускная квалификационная работа
Сингулярные интегралы.
Выполнила:
студентка V курса
математического факультета
Сколова Ирина Юрьевна
____________________
Научный руководитель:
старший преподаватель кафедры математического анализа и МПМ
Гукасов Артур Константинович
____________________
Рецензент:
кандидат физико-математических наук, доцент
Подгорная Ирина Иссаковна
____________________
Допущена к защите в ГАК
Зав. кафедрой ___________________ Крутихина М. В.
« » _______________
Декан факультета ___________________ Варанкина В. И.
« » _______________
Киров 2005
Оглавление
Введение………………………………………………………………………...с. 3
§1. Понятие сингулярного интеграла…………………………………………с. 6
§2. Представление функции сингулярным интегралом в заданной точке…с. 11
§3. Приложения в теории рядов Фурье.............................................................с. 18
§4. Сингулярный интеграл Пуассона................................................................с. 23
Литература……………………………………………………………………...с. 27
Введение
Цель работы – познакомиться с понятием сингулярного интеграла, рассмотреть представление функции сингулярным интегралом в заданной точке и приложения в теории рядов Фурье.
Основной вопрос теории сингулярных
интегралов состоит в установлении связи
предельных значений интеграла
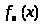 при
при
 со значением функции f
(t)
в точке x.
Важным также является вопрос о
представлении суммируемой функции
сингулярным интегралом в точках, где
эта функция служит производной своего
неопределенного интеграла, или в точках
Лебега. Теория сингулярных интегралов
имеет многочисленные приложения.
Например, вопрос о сходимости ряда Фурье
разрешается с помощью сингулярного
интеграла.
со значением функции f
(t)
в точке x.
Важным также является вопрос о
представлении суммируемой функции
сингулярным интегралом в точках, где
эта функция служит производной своего
неопределенного интеграла, или в точках
Лебега. Теория сингулярных интегралов
имеет многочисленные приложения.
Например, вопрос о сходимости ряда Фурье
разрешается с помощью сингулярного
интеграла.
Во всем дальнейшем интеграл будем понимать в смысле интеграла Лебега. Напомним, что функция называется суммируемой, если существует конечный интеграл от этой функции.
В работе нам будут необходимы следующие определения и теоремы.
Определение.
Если в точке x
будет
 и
и
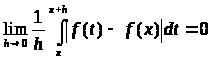 ,
то точка x
называется точкой Лебега
функции f
(t).
,
то точка x
называется точкой Лебега
функции f
(t).
Теорема (Н. Н. Лузин).
Пусть f
(x)
измеримая и почти везде конечная функция,
заданная на [a,
b].
Каково бы ни было δ>0, существует такая
непрерывная функция
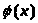 ,
что
,
что
 .
.
Если, в частности,
 ,
то и
,
то и
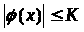 .
.
Теорему Н. Н. Лузина можно сформулировать и так: измеримая и почти везде конечная функция становится непрерывной, если пренебречь множеством сколь угодно малой меры.
Определение. Пусть
дано измеримое множество E.
Взяв произвольную точку x
и число h>0,
положим E(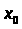 ,
h)=E∙[
,
h)=E∙[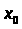 -h,
-h,
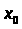 +h].
Это тоже измеримое множество.
+h].
Это тоже измеримое множество.
Предел отношения
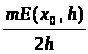 при h→0
называется плотностью
множества E
в точке
при h→0
называется плотностью
множества E
в точке
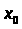 и обозначается через
и обозначается через
 .
.
Определение. Пусть
функция f
(x)
задана на сегменте [a,
b]
и
 .
Если существует такое измеримое множество
E,
лежащее на [a,
b]
и имеющее точку
.
Если существует такое измеримое множество
E,
лежащее на [a,
b]
и имеющее точку
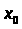 точкой плотности, что f
(x)
вдоль E
непрерывна в точке
точкой плотности, что f
(x)
вдоль E
непрерывна в точке
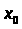 ,
то говорят, что f
(x)
аппроксимативно непрерывна
в точке
,
то говорят, что f
(x)
аппроксимативно непрерывна
в точке
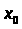 .
.
Определение. Измеримая функция f (x) называется функцией с суммируемым квадратом, или функцией, суммируемой с квадратом, если
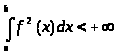 .
.
Множество всех функций с
суммируемым квадратом обозначается
символом
 .
.
Определение.
Пусть на сегменте [a,
b]
задана конечная функция f
(x).
Если всякому ε>0
отвечает такое δ>0,
что для любой конечной системы взаимно
не пересекающихся интервалов
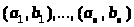 ,
для которой
,
для которой
 оказывается
оказывается
 ,
(3)
,
(3)
то говорят, что функция f (x) абсолютно непрерывна.
Не изменяя смысла определения,
можно условие (3) заменить более тяжелым
условием
 .
.
Определение.
Две функции f
(x)
и g(x),
заданные на сегменте [a,
b],
называются взаимно
ортогональными, если
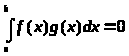 .
.
Определение.
Функция f
(x),
заданная на [a,
b],
называется нормальной,
если
 .
.
Определение.
Система функций
 ,
,
 ,
,
 ,
…, заданных на сегменте [a,
b],
называется ортонормальной
системой, если каждая
функция системы нормирована, а любые
две функции системы взаимно ортогональны.
,
…, заданных на сегменте [a,
b],
называется ортонормальной
системой, если каждая
функция системы нормирована, а любые
две функции системы взаимно ортогональны.
Определение.
Пусть
 есть ортонормальная система и f
(x)
некоторая функция из
есть ортонормальная система и f
(x)
некоторая функция из
 .
Числа
.
Числа
 называются коэффициентами
Фурье функции f
(x)
в системе
называются коэффициентами
Фурье функции f
(x)
в системе
 .
.
Ряд
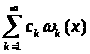 называется рядом Фурье
функции f
(x)
в системе
называется рядом Фурье
функции f
(x)
в системе
 .
.
§1. Понятие сингулярного интеграла
Чтобы познакомиться с идеей, лежащей в основе понятия сингулярного интеграла, начнем с примера.
Рассмотрим функцию
 . (1)
. (1)
Если n
и x
фиксированы, а t
меняется от 0 до 1, то эта функция есть
непрерывная функция от t.
Значит, для всякой суммируемой f
(t)
( )
можно образовать величину
)
можно образовать величину
 . (2)
. (2)
Докажем, что во всякой точке x (0<x<1), в которой функция f(t) непрерывна, будет
 . (3)
. (3)
Для этого прежде всего отметим,
что при

 . (4)
. (4)
Поэтому, чтобы установить (3),
достаточно показать, что при
 стремится к нулю разность
стремится к нулю разность
 .
.
Возьмем
произвольное
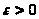 и найдем такое
и найдем такое
 ,
что при
,
что при
 будет
будет
 .
Считая, что
.
Считая, что
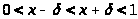 ,
представим
,
представим
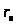 в форме
в форме
 .
.
Интеграл
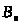 оценивается следующим образом:
оценивается следующим образом:
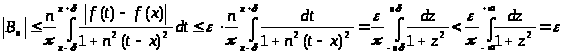 .
.
В интеграле
 будет
будет
 ,
поэтому
,
поэтому

 ,
,
где
 не зависит от n.
Аналогично
не зависит от n.
Аналогично
 и, следовательно,
и, следовательно,  ,
,
так что при достаточно больших
n
будет
 ,
т. е.
,
т. е.
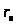 стремится к 0 с возрастанием n,
что и требовалось доказать.
стремится к 0 с возрастанием n,
что и требовалось доказать.
Соотношение (3) обеспечивают
следующие свойства функции
 :
при больших значениях n
те значения
:
при больших значениях n
те значения
 ,
которые отвечают сколько-нибудь заметно
удаленным от x
значениям t,
очень малы, так что величина интеграла
(2) определяется в основном значениями
подынтегральной функции в непосредственной
близости точки x.
Но около точки x
функция f
(t)
почти равна f
(x)
(т. к. она непрерывна при t=x).
Значит, если n
велико, то интеграл (2) мало изменяется
при замене f
(t)
на f
(x),
т. е. он почти равен интегралу
,
которые отвечают сколько-нибудь заметно
удаленным от x
значениям t,
очень малы, так что величина интеграла
(2) определяется в основном значениями
подынтегральной функции в непосредственной
близости точки x.
Но около точки x
функция f
(t)
почти равна f
(x)
(т. к. она непрерывна при t=x).
Значит, если n
велико, то интеграл (2) мало изменяется
при замене f
(t)
на f
(x),
т. е. он почти равен интегралу

и, в силу (4), почти равен f (x).
Функция
 ,
обладающая подобными свойствами, носит
название ядра.
,
обладающая подобными свойствами, носит
название ядра.
Определение.
Пусть функция
 (n=1,
2, …), заданная в квадрате (
(n=1,
2, …), заданная в квадрате ( ,
,
 ),
суммируема по t
при каждом фиксированном x.
Она называется ядром,
если
),
суммируема по t
при каждом фиксированном x.
Она называется ядром,
если
 при условии, что
при условии, что
 .
.
Определение. Интеграл
вида
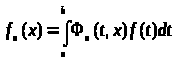 ,
где
,
где
 есть ядро, называется сингулярным
интегралом.
есть ядро, называется сингулярным
интегралом.
В теории сингулярных интегралов
очень важен вопрос установления связи
предельных значений интеграла
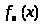 при
при
 со значением функции
со значением функции
f
(t)
в точке x.
Так как изменение значения функции f
(t)
в одной точке никак не отражается на
величине
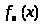 ,
то необходимо потребовать, чтобы значение
f
(x)
функции f
(t)
в точке x
было как-то связано с ее значениями в
близких точках. Простейшая форма такой
связи есть непрерывность функции f
(t)
в точке t=x.
Другими формами связи могут служить
аппроксимативная непрерывность,
требование, чтобы x
была точкой Лебега функции f
(t),
и т. п.
,
то необходимо потребовать, чтобы значение
f
(x)
функции f
(t)
в точке x
было как-то связано с ее значениями в
близких точках. Простейшая форма такой
связи есть непрерывность функции f
(t)
в точке t=x.
Другими формами связи могут служить
аппроксимативная непрерывность,
требование, чтобы x
была точкой Лебега функции f
(t),
и т. п.
Теорема 1 (А. Лебег).
Пусть на [a,
b]
задана последовательность измеримых
функций
 ,
,
 ,
,
 ,
… Если существует такая постоянная K,
что при всех n
и t
будет
,
… Если существует такая постоянная K,
что при всех n
и t
будет
 , (5)
, (5)
и если при всяком c
( )
будет
)
будет
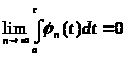 , (6)
, (6)
то, какова бы ни была суммируемая на [a, b] функция f (t), справедливо равенство
 . (7)
. (7)
Доказательство.
Если
 есть сегмент, содержащийся в [a,
b],
то из (6) следует, что
есть сегмент, содержащийся в [a,
b],
то из (6) следует, что
 . (8)
. (8)
Рассмотрим непрерывную
функцию f
(t),
и для наперед заданного
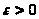 разложим [a,
b]
точками
разложим [a,
b]
точками
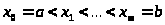 на столь малые части, чтобы
в каждой из них колебание f
(t)
было меньше, чем ε.
на столь малые части, чтобы
в каждой из них колебание f
(t)
было меньше, чем ε.
Тогда
 .
(9)
.
(9)
Но
 ,
так что первая сумма из (9) не больше, чем
Kε(b-a).
Вторая же сумма (9), в силу (8), стремится
к нулю с возрастанием n
и для
,
так что первая сумма из (9) не больше, чем
Kε(b-a).
Вторая же сумма (9), в силу (8), стремится
к нулю с возрастанием n
и для
 окажется меньшей, чем ε.
Для этих n
будет
окажется меньшей, чем ε.
Для этих n
будет
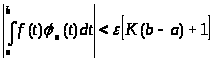 ,
,
так что (7) доказано для непрерывной функции f(t).
Пусть f
(t)
измеримая ограниченная
функция
 .
.
Возьмем ε>0
и, пользуясь теоремой Н. Н. Лузина, найдем
такую непрерывную функцию g(t),
что
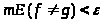 ,
,
 .
.
Тогда
 .
.
Но
 .
.
Интеграл
 по уже доказанному стремится к нулю и
для достаточно больших n
становится меньше ε.
Значит, для этих n
будет
по уже доказанному стремится к нулю и
для достаточно больших n
становится меньше ε.
Значит, для этих n
будет
 ,
,
что доказывает (7) для случая ограниченной измеримой функции.
Пусть f (t) произвольная суммируемая функция.
Возьмем ε>0
и, пользуясь абсолютной непрерывностью
интеграла, найдем такое δ>0,
чтобы для любого измеримого множества
 с мерой me<δ
было
с мерой me<δ
было
 .
.
Сделав это, найдем такую измеримую
ограниченную функцию g(t),
чтобы было
 .
Это возможно по
.
Это возможно по
Теореме. Пусть
на множестве Е задана измеримая, почти
везде конечная функция f
(x).
Каково бы ни было ε>0, существует
измеримая ограниченная функция g(x)
такая, что
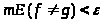 .
.
Можно считать, что на множестве
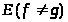 функция g(t)
равна нулю.
функция g(t)
равна нулю.
Тогда
 .
.
Но
 .
.
Интеграл же
 при достаточно больших n
будет меньше ε,
и при этих n
окажется
при достаточно больших n
будет меньше ε,
и при этих n
окажется
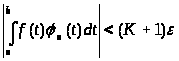 ,
что и доказывает теорему.
,
что и доказывает теорему.
Пример. Пусть
 .
Тогда
.
Тогда
 и
и
 .
Следовательно выполнены оба условия
теоремы Лебега. Аналогично рассматривается
случай
.
Следовательно выполнены оба условия
теоремы Лебега. Аналогично рассматривается
случай
 .
Таким образом доказана
.
Таким образом доказана
Теорема 2 (Риман-Лебег). Для любой суммируемой на [a, b] функции
f
(t)
будет
 .
.
В частности, коэффициенты
Фурье
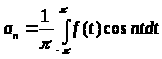 ,
,
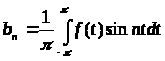 произвольной суммируемой
функции стремятся к нулю при
произвольной суммируемой
функции стремятся к нулю при
 .
.
Если соотношение (7) имеет место
для всякой суммируемой на [a,
b]
функции f
(t),
то мы будем говорить, что последовательность
 слабо сходится к нулю.
слабо сходится к нулю.
§2. Представление функции сингулярным интегралом в заданной точке
Во всем дальнейшем будем считать,
что ядро
 при фиксированных n
и x
ограничено. Тогда сингулярный интеграл
при фиксированных n
и x
ограничено. Тогда сингулярный интеграл
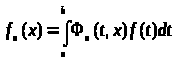 имеет смысл при любой суммируемой
функции f
(t).
имеет смысл при любой суммируемой
функции f
(t).
Теорема 1 (А. Лебег).
Если при фиксированном x(a<x<b)
и любом δ>0 ядро
 слабо сходится к нулю в
каждом из промежутков [a,
x-δ],
слабо сходится к нулю в
каждом из промежутков [a,
x-δ],
[x+δ,
b]
и
 ,
где H(x)
не зависит от n,
то, какова бы ни была суммируемая функция
f
(t),
непрерывная в точке x,
справедливо равенство
,
где H(x)
не зависит от n,
то, какова бы ни была суммируемая функция
f
(t),
непрерывная в точке x,
справедливо равенство
 .
.
Доказательство.
Так как
 есть ядро, то
есть ядро, то
 ,
,
и достаточно обнаружить, что
 .
.
С этой целью, взяв ε>0,
найдем такое δ>0,
что при
 будет
будет
 .
.
Это возможно в силу непрерывности функции f в точке x.
Тогда при любом n
 .
.
Но каждый из интегралов
 ,
,
 при
при
 стремится к нулю, т. к.
стремится к нулю, т. к.
 слабо сходится к нулю в каждом из
промежутков [a,
x-δ],
[x+δ,
b].
Поэтому для
слабо сходится к нулю в каждом из
промежутков [a,
x-δ],
[x+δ,
b].
Поэтому для
 каждый из них будет по абсолютной
величине меньше ε/3.
каждый из них будет по абсолютной
величине меньше ε/3.
И для этих n
окажется
 ,
что и требовалось доказать.
,
что и требовалось доказать.
Эта теорема относится к представлению суммируемой функции в точках непрерывности, но суммируемая функция, вообще говоря, не имеет ни одной точки непрерывности, что понижает интерес этой теоремы.
Больший интерес представляет вопрос о представлении суммируемой функции в тех точках, где эта функция служит производной своего неопределенного интеграла, или в точках Лебега, так как и те и другие точки заполняют почти весь сегмент задания функции. Перейдем к рассмотрению этого вопроса.
Лемма (И. П. Натансон). Пусть на сегменте [a, b] дана суммируемая функция f (t), обладающая тем свойством, что
 . (1)
. (1)
Какова бы ни была неотрицательная убывающая функция g(t), заданная и суммируемая на [a, b], интеграл
 (2)
(2)
существует (может быть как несобственный при t=a) и справедливо неравенство
 . (3)
. (3)
В пояснение условий леммы
заметим, что не исключается случай,
когда
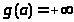 .
Если же
.
Если же
 ,
то функция g(t)
ограничена, и интеграл (2) существует
как обычный интеграл Лебега.
,
то функция g(t)
ограничена, и интеграл (2) существует
как обычный интеграл Лебега.
Переходя к доказательству леммы, заметим, что не ограничивая общности, можно принять, что g(b)=0. Действительно, если бы это не было так, то можно было ввести вместо g(t) функцию g*(t), определив ее равенствами
 g(t),
если
g(t),
если
 ,
,
g*(t)=
0, если t=b.
Доказав теорему для g*(t), мы затем смогли бы всюду заменить g*(t) на g(t), т. к. такая замена не отражается на величине интересующих нас интегралов. Итак, считаем, что g(b)=0.
Пусть a<α<b. На сегменте [α, b] функция g(t) ограничена, и интеграл
 (4)
(4)
заведомо существует. Если положить
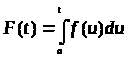 ,
то интеграл (4) можно записать в форме
интеграла Стилтьеса
,
то интеграл (4) можно записать в форме
интеграла Стилтьеса
 ,
,
откуда, после интегрирования по частям, находим
 .
.
Но, в силу (1), мы имеем, что для
любого h
из интервала [0,
t-a]
выполняется неравенство
 и следовательно
и следовательно
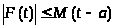 , (5)
, (5)
а так как g(t) убывает, то
 . (6)
. (6)
Значит
 .
С другой стороны, функция –g(t)
возрастает. Отсюда и из (5) следует, что
.
С другой стороны, функция –g(t)
возрастает. Отсюда и из (5) следует, что
 .
.
Преобразуем стоящий справа интеграл по формуле интегрирования по частям:
 .
.
Отсюда, учитывая (6), следует, что
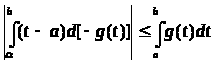 .
.
Сопоставляя все сказанное, получаем:
 . (7)
. (7)
Хотя это неравенство установлено
при предположении, что g(b)=0,
но оно останется верным и без этого
предположения. Значит, можно заменить
здесь предел b
на β, где α<β<b.
Но тогда, устремляя α
и β к a,
получим  ,
,
чем доказывается существование
интеграла (2). Если в (7) перейти к пределу
при
 ,
то получим (3). Лемма доказана. (В оценке
(3) множителя M
уменьшить нельзя, так как при f
(t)=1
в (3) достигается равенство.)
,
то получим (3). Лемма доказана. (В оценке
(3) множителя M
уменьшить нельзя, так как при f
(t)=1
в (3) достигается равенство.)
Теорема 2 (П. И.
Романовский). Пусть
ядро
 положительно и обладает следующим
свойством: при фиксированных n
и x
ядро
положительно и обладает следующим
свойством: при фиксированных n
и x
ядро
 ,
как функция одного лишь t,
возрастает в сегменте [a,
x]
и убывает в сегменте
,
как функция одного лишь t,
возрастает в сегменте [a,
x]
и убывает в сегменте
[x, b].
Тогда для любой суммируемой
функции f
(t),
которая в точке x
является производной своего неопределенного
интеграла, будет  .
.
Доказательство.
Так как
 есть ядро, то
есть ядро, то
 и достаточно проверить, что
и достаточно проверить, что
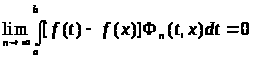 .
.
Разбивая последний интеграл на два, распространенные на сегменте
[a, x] и [x, b], рассмотрим второй из них, так как первый изучается аналогично.
Возьмем ε>0
и найдем такое δ>0,
что при
 будет
будет
 ,
,
что возможно, так как f
(t)
в точке t=x
есть производная своего неопределенного
интеграла. То есть
 и
и
 .
.
Тогда по предыдущей лемме
 .
.
Так как
 есть ядро, то
есть ядро, то
 .
.
Величина, имеющая конечный
предел, ограничена. Значит, существует
постоянная K(x)
такая, что
 .
.
Таким образом,
 .
.
С другой стороны, если
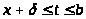 ,
то
,
то
 .
.
Значит функции
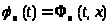 на сегменте [x+δ,
b]
равномерно ограничены и выполнено
условие (5) теоремы Лебега из §1. Но второе
ее условие, т. е. условие (6), также выполнено
для этих функций, т. к.
на сегменте [x+δ,
b]
равномерно ограничены и выполнено
условие (5) теоремы Лебега из §1. Но второе
ее условие, т. е. условие (6), также выполнено
для этих функций, т. к.
 является ядром. Следовательно
является ядром. Следовательно
 на сегменте [x+δ,
b]
слабо сходится к нулю, и для достаточно
больших n
будет
на сегменте [x+δ,
b]
слабо сходится к нулю, и для достаточно
больших n
будет
 .
.
При этих n окажется
 ,
,
так что
 .
.
Теорема доказана.
В качестве примера ее приложения
рассмотрим интеграл
Вейерштрасса
 .
.
Функция
 есть ядро, т. к. при α<x<β
есть ядро, т. к. при α<x<β
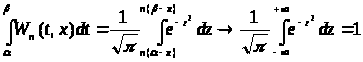 .
.
Эта функция положительна, и она
возрастает при
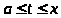 и убывает при
и убывает при
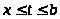 .
Значит, для всякой
.
Значит, для всякой
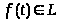 будет
будет
 в каждой точке x,
где f
(t)
есть производная своего неопределенного
интеграла.
в каждой точке x,
где f
(t)
есть производная своего неопределенного
интеграла.
Определение.
Функция Ψ(t,
x)
называется горбатой
мажорантой функции
 ,
если
,
если
 и если Ψ(t,
x)
при фиксированном x
возрастает на сегменте [a,
x]
и убывает на сегменте [x,
b].
и если Ψ(t,
x)
при фиксированном x
возрастает на сегменте [a,
x]
и убывает на сегменте [x,
b].
Теорема 3 (Д. К.
Фаддеев). Если ядро
 при каждом n
имеет такую горбатую мажоранту
при каждом n
имеет такую горбатую мажоранту
 ,
что
,
что
 ,
,
где K(x)
зависит лишь от x,
то для любой
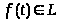 ,
имеющей точку t=x
точкой Лебега, будет справедливо
равенство
,
имеющей точку t=x
точкой Лебега, будет справедливо
равенство
 .
.
Доказательство. Достаточно доказать, что
 .
.
Возьмем ε>0
и найдем такое δ>0,
что при
 будет
будет
 .
.
По лемме имеем
 .
.
С другой стороны, в сегменте
[x+δ,
b]
последовательность
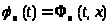 слабо сходится к нулю, т. к. при
слабо сходится к нулю, т. к. при
 будет
будет
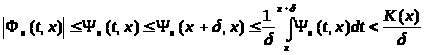 .
.
Следовательно для достаточно больших n будет
 .
.
При этих n
окажется
 ,
,
так что
 .
Теорема доказана.
.
Теорема доказана.
§3. Приложения в теории рядов Фурье
Во введении мы уже определили
понятие ряда Фурье функции f
(x)
по любой ортонормальной системе
 .
В частности, если речь идет о
тригонометрической системе
.
В частности, если речь идет о
тригонометрической системе
 , (1)
, (1)
то рядом Фурье функции f (x) служит ряд
 , (2)
, (2)
где
 ,
,
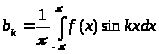 . (3)
. (3)
Во введении предполагали, что
 .
Это предположение обеспечило существование
коэффициентов Фурье
.
Это предположение обеспечило существование
коэффициентов Фурье
 функции f
(x)
в любой ортонормальной системе. Но
функции системы (1) ограничены. Поэтому
коэффициенты (3), а с ними и ряд (2), можно
образовать для любой суммируемой
функции.
функции f
(x)
в любой ортонормальной системе. Но
функции системы (1) ограничены. Поэтому
коэффициенты (3), а с ними и ряд (2), можно
образовать для любой суммируемой
функции.
Вопрос о сходимости ряда (2)
приводится к исследованию некоторого
сингулярного интеграла. Если
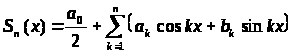 ,
то, в силу (3),
,
то, в силу (3),
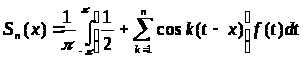 .
.
Выведем формулу для упрощения выражения в скобках. Для этого сложим равенства
 (k=0,
1, …, n-1),
(k=0,
1, …, n-1),
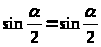 .
.
Это дает
 ,
откуда следует равенство
,
откуда следует равенство
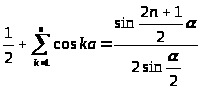 , (4)
, (4)
Пользуясь этой формулой, придадим
сумме
 вид
вид
 . (5)
. (5)
Этот интеграл есть сингулярный интеграл Дирихле.
Рассмотрим вопрос о суммировании
ряда (2) по способу Чезаро. Этот способ
состоит в отыскании предела среднего
арифметического первых n
сумм
 :
:

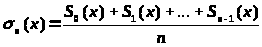 . (6)
. (6)
В случае сходимости ряда (2) в
точке x
последовательность
 сходится к сумме ряда, но эта
последовательность может сходиться и
тогда, когда ряд (2) расходится.
сходится к сумме ряда, но эта
последовательность может сходиться и
тогда, когда ряд (2) расходится.
Для исследования
 преобразуем ее с помощью формулы (5)
преобразуем ее с помощью формулы (5)
 .
.
Но
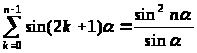 . (7)
. (7)
Действительно, складывая равенства
 (k=0,
1, …, n-1),
(k=0,
1, …, n-1),
находим
 ,
откуда и следует (7).
,
откуда и следует (7).
С помощью (7) получаем
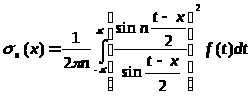 . (8)
. (8)
Интеграл (8) есть сингулярный интеграл Фейера. Покажем, что для него выполнены условия теоремы Фаддеева.
Для этого рассмотрим функцию f
(t)=1.
Вычисляя ее коэффициенты Фурье по
формулам (3), получим
 (k=1,
2, …).
(k=1,
2, …).
Значит, для этой функции
 (n=0,
1, 2, …), а следовательно и
(n=0,
1, 2, …), а следовательно и
 .
.
Но выражая
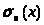 интегралом Фейера, получим, что
интегралом Фейера, получим, что
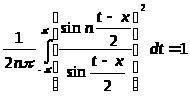 . (9)
. (9)
Заметив это, рассмотрим точку
 .
Пусть
.
Пусть
 .
Если
.
Если
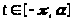 ,
то
,
то
 ,
и, следовательно,
,
и, следовательно,
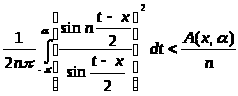 ,
где A(x,
α)
не зависит от n.
,
где A(x,
α)
не зависит от n.
Отсюда следует, что
 .
.
Аналогично убедимся, что интеграл стремится к нулю по промежутку [β, π]. Сопоставляя это с (9), находим, что
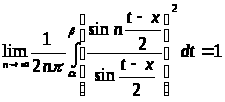 ,
,
так что функция
 есть ядро.
есть ядро.
Для этого ядра можно построить
горбатую мажоранту. Заметим, что
 .
Отсюда
.
Отсюда
 .
Но
.
Но
 .
.
Следовательно
 и
и
 . (10)
. (10)
С другой стороны, когда
 ,
то
,
то
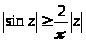 ,
так что
,
так что
 . (11)
. (11)
Так как
 ,
,
 ,
то
,
то
 может оказаться и больше, чем
может оказаться и больше, чем
 .
Но это несущественно. Если положим
.
Но это несущественно. Если положим
 ,
,
 ,
то разность между интегралом Фейера
(8) и интегралом
,
то разность между интегралом Фейера
(8) и интегралом

при возрастании n
стремится к нулю (т. к., например, при
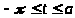 будет
будет
 ),
поэтому все рассуждения можно вести
для интеграла
),
поэтому все рассуждения можно вести
для интеграла
 .
.
Из (10) и (11) следует, что
 .
.
Функция
 есть горбатая мажоранта ядра Фейера.
есть горбатая мажоранта ядра Фейера.
Но
 ,
т. е. интегралы от мажоранты ограничены
числом, не зависящим от n.
,
т. е. интегралы от мажоранты ограничены
числом, не зависящим от n.
Итак, интеграл Фейера удовлетворяет условиям теоремы
Д. К. Фаддеева. Отсюда следует
Теорема 1 (Л. Фейер – А. Лебег). Почти везде на [-π, +π] будет
 . (12)
. (12)
Это соотношение выполняется во всех точках Лебега и тем более во всех точках непрерывности функции f (t), лежащих внутри [-π, +π].
Тригонометрическая система
полна. Это означает, что всякая функция
 ,
у которой все коэффициенты Фурье (3)
равны нулю, эквивалентна нулю. Избавимся
от ограничения, что f (x)
суммируема с квадратом. Справедлива
следующая
,
у которой все коэффициенты Фурье (3)
равны нулю, эквивалентна нулю. Избавимся
от ограничения, что f (x)
суммируема с квадратом. Справедлива
следующая
Теорема 2. Если все коэффициенты Фурье (3) суммируемой функции
f (x) равны нулю, то f (x) эквивалентна нулю.
В самом деле, в
этом случае
 и, следовательно, f
(x)=0
во всех точках, где имеет место (12), т. е.
почти везде.
и, следовательно, f
(x)=0
во всех точках, где имеет место (12), т. е.
почти везде.
Теорема 1 позволяет делать
некоторые высказывания и о поведении
сумм
 .
Для этого заметим, что
.
Для этого заметим, что
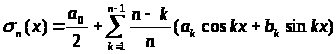 ,
,
так что
 .
.
Отсюда
 .
.
§4. Сингулярный интеграл Пуассона
Пусть точка x
есть точка
d
суммируемой функции f
(t),
если в этой точке производная
неопределенного интеграла функции f
(t)
равна f
(x)
(причем
 ).
).
Интеграл
 (0<r<1)
есть сингулярный интеграл Пуассона.
Если x
(-π<x<π)
есть точка d
суммируемой функции f
(t),
то
(0<r<1)
есть сингулярный интеграл Пуассона.
Если x
(-π<x<π)
есть точка d
суммируемой функции f
(t),
то
 (П. Фату).
(П. Фату).
1) Докажем, что
 - ядро. Т. к. ядро является 2π-периодической
функцией, то интеграл от этой функции,
рассматриваемый на периоде, не зависит
от x.
Рассмотрим
- ядро. Т. к. ядро является 2π-периодической
функцией, то интеграл от этой функции,
рассматриваемый на периоде, не зависит
от x.
Рассмотрим
 при x=0.
при x=0.
 .
.
Для вычисления интеграла используем универсальную тригонометрическую подстановку и получим
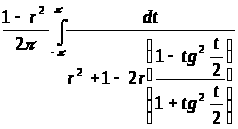 . (1)
. (1)
Обозначим
 ,
тогда
,
тогда
 ,
а
,
а
 .
.
Выражение (1) будет равно




 при 0<r<1.
при 0<r<1.
Получили, что
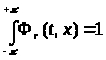 и
и - ядро.
- ядро.
2) Докажем, что
 .
.
 ,
,
 .
.
Тогда
 .
Следовательно достаточно проверить,
что
.
Следовательно достаточно проверить,
что
 .
.
Найдем
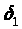 такое,
что на интервале [x-
такое,
что на интервале [x-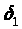 ,
x]
ядро
,
x]
ядро
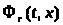 возрастает, а на [x,
x+
возрастает, а на [x,
x+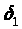 ]
убывает. Это возможно, т. к. производная
функции
]
убывает. Это возможно, т. к. производная
функции
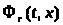 меняет знак с плюса на минус при переходе
через точку x:
меняет знак с плюса на минус при переходе
через точку x:
 .
.
Возьмем ε>0
и найдем такое δ
(0<δ<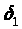 ),
что при
),
что при
 будет
будет
 ,
что возможно, так как x
есть точка d,
т.е. f
(t)
в точке t=x
есть производная своего неопределенного
интеграла.
,
что возможно, так как x
есть точка d,
т.е. f
(t)
в точке t=x
есть производная своего неопределенного
интеграла.
Тогда по лемме И. П. Натансона
 ,
т. к.
,
т. к.
 есть ядро, и
есть ядро, и
 .
.
Таким образом, на интервале [x,
x+δ]
справедливо неравенство
 .
На [x-δ,
x]
интеграл рассматривается аналогично
в силу симметричности ядра на интервале
[x-δ,
x+δ]
относительно точки x.
.
На [x-δ,
x]
интеграл рассматривается аналогично
в силу симметричности ядра на интервале
[x-δ,
x+δ]
относительно точки x.
Рассмотрим
 за пределами [x-δ,
x+δ],
т.е. на
за пределами [x-δ,
x+δ],
т.е. на
[-π, x-δ,] и на [x+δ, π].
В этих случаях выполняются неравенства
 ,
,
 .
.
Тогда
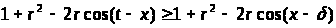 и
и
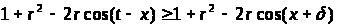 .
.
Следовательно
 ,
т. к.
,
т. к.
 ,
и знаменатель дроби не равен нулю.
,
и знаменатель дроби не равен нулю.
Аналогично
 .
.
То есть
 на интервалах [-π, x-δ,]
и [x+δ,
π].
на интервалах [-π, x-δ,]
и [x+δ,
π].
При r, достаточно близких к 1, получим
 и
и
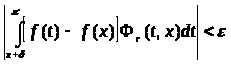 .
.
При этих r
окажется
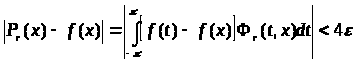 ,
,
так что
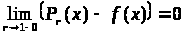 и
и
 .
.
Таким образом, доказано, что
 (0<r<1)
есть сингулярный интеграл.
(0<r<1)
есть сингулярный интеграл.
Литература
Натансон И. П. Теория функций вещественной переменной. – М.: Наука, 1974.
Кашин Б. С., Саакян А. А. Ортогональные ряды. –
Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. – М.: Наука, 1968.