–†–µ—И–µ–љ–Є–µ —Н–Ї–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Є—Е –Ј–∞–і–∞—З
–Ч–∞–і–∞–љ–Є–µ 1
–Я—А–µ–і–њ—А–Є—П—В–Є—О –і–ї—П –Є–Ј–≥–Њ—В–Њ–≤–ї–µ–љ–Є—П –љ–∞–±–Њ—А–Њ–≤ –µ–ї–Њ—З–љ—Л—Е —Г–Ї—А–∞—И–µ–љ–Є–є –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Є–Ј–≥–Њ—В–Њ–≤–Є—В—М –Є—Е —Б–Њ—Б—В–∞–≤–љ—Л–µ —З–∞—Б—В–Є - —И–∞—А, –Ї–Њ–ї–Њ–Ї–Њ–ї—М—З–Є–Ї, –Љ–Є—И—Г—А–∞. –≠—В–Є –і–∞–љ–љ—Л–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ—Л –≤ —В–∞–±–ї–Є—Ж–µ:
|
–Э–∞–Є–Љ–µ–љ–Њ–≤–∞–љ–Є–µ —Б–Њ—Б—В–∞–≤–љ—Л—Е —З–∞—Б—В–µ–є |
–Т–Є–і—Л –љ–∞–±–Њ—А–Њ–≤ |
|||
|
1 |
2 |
3 |
4 |
|
|
–®–∞—А |
5 |
6 |
8 |
10 |
|
–Ъ–Њ–ї–Њ–Ї–Њ–ї—М—З–Є–Ї |
3 |
4 |
6 |
0 |
|
–Ь–Є—И—Г—А–∞ |
0 |
3 |
5 |
8 |
–Т —Б–≤–Њ—О –Њ—З–µ—А–µ–і—М –і–ї—П –Є–Ј–≥–Њ—В–Њ–≤–ї–µ–љ–Є—П —Н—В–Є—Е —Б–Њ—Б—В–∞–≤–љ—Л—Е —З–∞—Б—В–µ–є –љ–µ–Њ–±—Е–Њ–і–Є–Љ—Л —В—А–Є –≤–Є–і–∞ —Б—Л—А—М—П - —Б—В–µ–Ї–ї–Њ (–≤ –≥), –њ–∞–њ—М–µ-–Љ–∞—И–µ (–≤ –≥), —Д–Њ–ї—М–≥–∞ (–≤ –≥), –њ–Њ—В—А–µ–±–љ–Њ—Б—В–Є –≤ –Ї–Њ—В–Њ—А–Њ–Љ –Њ—В—А–∞–ґ–µ–љ—Л –≤ —Б–ї–µ–і—Г—О—Й–µ–є —В–∞–±–ї–Є—Ж–µ
|
–Т–Є–і —Б—Л—А—М—П |
–°–Њ—Б—В–∞–≤–љ—Л–µ —Н–ї–µ–Љ–µ–љ—В—Л |
||
|
–®–∞—А |
–Ъ–Њ–ї–Њ–Ї–Њ–ї—М—З–Є–Ї |
–Ь–Є—И—Г—А–∞ |
|
|
–°—В–µ–Ї–ї–Њ |
5 |
0 |
0 |
|
–Я–∞–њ—М–µ-–Љ–∞—И–µ |
0 |
4 |
0 |
|
–§–Њ–ї—М–≥–∞ |
3 |
0 |
75 |
–Ґ—А–µ–±—Г–µ—В—Б—П:
1) –Њ–њ—А–µ–і–µ–ї–Є—В—М –њ–Њ—В—А–µ–±–љ–Њ—Б—В–Є –≤ —Б—Л—А—М–µ –і–ї—П –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П –њ–ї–∞–љ–∞ –њ–Њ –Є–Ј–≥–Њ—В–Њ–≤–ї–µ–љ–Є—О –Ї–Њ–Љ–њ–ї–µ–Ї—В–Њ–≤ –њ–µ—А–≤–Њ–≥–Њ, –≤—В–Њ—А–Њ–≥–Њ, —В—А–µ—В—М–µ–≥–Њ –Є —З–µ—В–≤–µ—А—В–Њ–≥–Њ –≤–Є–і–∞ –≤ –Ї–Њ–ї–Є—З–µ—Б—В–≤–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ x>1>, x>2,> x>3 >–Є x>4 >—И—В—Г–Ї;
2) –њ—А–Њ–≤–µ—Б—В–Є –њ–Њ–і—Б—З–µ—В—Л –і–ї—П –Ј–љ–∞—З–µ–љ–Є–є x>1 >= 500, x>2> = 400, x>3 >= 300 –Є x>4>=200.
–†–µ—И–µ–љ–Є–µ: —Б–Њ—Б—В–∞–≤–Є–Љ —Г—Б–ї–Њ–≤–Є—П –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —З–Є—Б–ї–∞ –і–µ—В–∞–ї–µ–є –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В —З–Є—Б–ї–∞ –Є –≤–Є–і–∞ –љ–∞–±–Њ—А–Њ–≤. –Я—Г—Б—В—М n>1>, n>2> –Є n>3> - —З–Є—Б–ї–Њ —И–∞—А–Њ–≤, –Ї–Њ–ї–Њ–Ї–Њ–ї—М—З–Є–Ї–Њ–≤ –Є –Љ–Є—И—Г—А—Л, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.
–Ґ–Њ–≥–і–∞ —Г—Б–ї–Њ–≤–Є—П –±—Г–і—Г—В –≤—Л–≥–ї—П–і–µ—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
n>1> = 5x>1> + 6x>2> + 8x>3> + 10x>4>
n>2> = 3x>1> + 4x>2> + 6x>3>
n>3> = 3x>2> + 5x>3> + 8x>4>
–°–Њ—Б—В–∞–≤–Є–Љ —Г—Б–ї–Њ–≤–Є—П –Њ–њ—А–µ–і–µ–ї—П—О—Й–Є–µ –њ–Њ—В—А–µ–±–љ–Њ—Б—В–Є –≤ —Б—Л—А—М–µ –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В –≤–Є–і–∞ –і–µ—В–∞–ї–µ–є. –Я—Г—Б—В—М y>1>, y>2> –Є y>3> - –њ–Њ—В—А–µ–±–љ–Њ—Б—В–Є –≤ —Б—В–µ–Ї–ї–µ, –њ–∞–њ—М–µ-–Љ–∞—И–µ –Є —Д–Њ–ї—М–≥–µ, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ:
y>1> = 5n>1>
y>2> = 4n>2>
y>3> = 3n>1> + 75n>3>
–Ґ–µ–њ–µ—А—М –њ–Њ–і—Б—В–∞–≤–Є–Љ –≤–Љ–µ—Б—В–Њ n>i> - –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ —А–∞–љ–µ–µ —А–∞–≤–µ–љ—Б—В–≤–∞.
y>1> = 5¬Ј (5x>1> + 6x>2> + 8x>3> + 10x>4>) = 25x>1> + 30x>2> + 40x>3> + 50x>4>
y>2> = 4¬Ј (3x>1> + 4x>2> + 6x>3>) = 12x>1> + 16x>2> + 24x>3>
y>3> = 3¬Ј (5x>1> + 6x>2> + 8x>3> + 10x>4>) + 75¬Ј (3x>2> + 5x>3> + 8x>4>) = 15x>1> + 243x>2> + 399x>3> + 630x>4>
–Я—А–Њ–≤–µ–і–µ–Љ –њ–Њ–і—Б—З–µ—В—Л –і–ї—П –Ј–љ–∞—З–µ–љ–Є–є
x>1 >= 500, x>2> = 400, x>3 >= 300 –Є x>4>=200.
y>1> = 25 * 500 + 30 * 400 + 40 * 300 + 50 * 200 = 46500 –≥.
y>2> = 12 * 500 + 16 * 400 + 24 * 300 = 19600 –≥.
y>3> = 15 * 500 + 243 * 400 + 399 * 300 + 630 * 200 = 350400 –≥.
–Ч–∞–і–∞–љ–Є–µ 2
–Я—Г—Б—В—М a>ij>> - >–Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ–і—Г–Ї—Ж–Є–Є j, –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–љ–Њ–є –њ—А–µ–і–њ—А–Є—П—В–Є–µ–Љ i, –∞ b>i>> - >—Б—В–Њ–Є–Љ–Њ—Б—В—М –≤—Б–µ–є –њ—А–Њ–і—Г–Ї—Ж–Є–Є –њ—А–µ–і–њ—А–Є—П—В–Є—П i –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–є –Њ—В—А–∞—Б–ї–Є. –Ч–љ–∞—З–µ–љ–Є—П a>ij> –Є b>i>> >–Ј–∞–і–∞–љ—Л –Љ–∞—В—А–Є—Ж–∞–Љ–Є A –Є –Т —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ґ—А–µ–±—Г–µ—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М —Ж–µ–љ—Г –µ–і–Є–љ–Є—Ж—Л –њ—А–Њ–і—Г–Ї—Ж–Є–Є –Ї–∞–ґ–і–Њ–≥–Њ –≤–Є–і–∞, –њ—А–Њ–Є–Ј–≤–Њ–і–Є–Љ–Њ–є –њ—А–µ–і–њ—А–Є—П—В–Є—П–Љ–Є –Њ—В—А–∞—Б–ї–Є. –Т —Е–Њ–і–µ –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П –Ј–∞–і–∞–љ–Є—П –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Б–Њ—Б—В–∞–≤–Є—В—М —Б–Є—Б—В–µ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є–є, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й—Г—О —Г—Б–ї–Њ–≤–Є—П–Љ, –Є —А–µ—И–Є—В—М –µ–µ —В—А–µ–Љ—П —Б–њ–Њ—Б–Њ–±–∞–Љ–Є (–Љ–∞—В—А–Є—З–љ—Л–є –Љ–µ—В–Њ–і, –Љ–µ—В–Њ–і –Ъ—А–∞–Љ–µ—А–∞, –Љ–µ—В–Њ–і –У–∞—Г—Б—Б–∞).
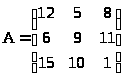 ,
,
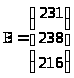
–†–µ—И–µ–љ–Є–µ:
–°–Њ—Б—В–∞–≤–Є–Љ —Б–Є—Б—В–µ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є–є:

–Ь–∞—В—А–Є—З–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –≤—Л–≥–ї—П–і–Є—В —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
A ¬Ј X = B
–Ф–Њ–Љ–љ–Њ–ґ–Є–Љ —Б–ї–µ–≤–∞ –Ї–∞–ґ–і—Г—О –Є–Ј —З–∞—Б—В–µ–є —Г—А–∞–≤–љ–µ–љ–Є—П –љ–∞ –Љ–∞—В—А–Є—Ж—Г A-1
A-1 ¬Ј A ¬Ј X = A-1 ¬Ј B; E ¬Ј X = A-1 ¬Ј B; X = A-1 ¬Ј B
–Э–∞–є–і–µ–Љ –Њ–±—А–∞—В–љ—Г—О –Љ–∞—В—А–Є—Ж—Г A-1
ќФ = 12 * 9 * 1 + 6 * 8 * 10 + 15 * 5 * 11 - 15 * 9 * 8 - 6 * 5 * 1 - 12 * 10 * 11 = - 1017
 ;
;

 =
=
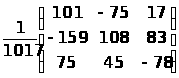
X
=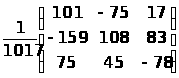 ¬Ј
¬Ј =
=
 =
=

–†–µ—И–Є–Љ —Б–Є—Б—В–µ–Љ—Г –Љ–µ—В–Њ–і–Њ–Љ –Ъ—А–∞–Љ–µ—А–∞
ќФ = - 1017
ќФ>1> =
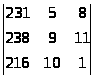 =
231 * 9 * 1 + 238 * 8 * 10 + 216 * 5 * 11 - 216 * 9 * 8 - 238 * 5 * 1
- - 231 * 10 * 11 = - 9153
=
231 * 9 * 1 + 238 * 8 * 10 + 216 * 5 * 11 - 216 * 9 * 8 - 238 * 5 * 1
- - 231 * 10 * 11 = - 9153
ќФ>2> =
 =
12 * 238 * 1 + 6 * 8 * 216 + 15 * 231 * 11 - 15 * 238 * 8 - 6 * 231 *
1 - 12 * 216 * 11 = - 7119
=
12 * 238 * 1 + 6 * 8 * 216 + 15 * 231 * 11 - 15 * 238 * 8 - 6 * 231 *
1 - 12 * 216 * 11 = - 7119
ќФ>3> =
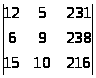 =
12 * 9 * 216 + 6 * 231 * 10 + 15 * 5 * 238 - 15 * 9 * 231 - 6 * 5 *
216 - 12 * 10 * 238 = - 11187
=
12 * 9 * 216 + 6 * 231 * 10 + 15 * 5 * 238 - 15 * 9 * 231 - 6 * 5 *
216 - 12 * 10 * 238 = - 11187
x>1> = ќФ>1/>ќФ = - 9153/ (- 1017) = 9
x>2> = ќФ>2/>ќФ = - 7119/ (- 1017) = 7
x>3> = ќФ>3/>ќФ = - 11187/ (- 1017) = 11
–†–µ—И–Є–Љ —Б–Є—Б—В–µ–Љ—Г –Љ–µ—В–Њ–і–Њ–Љ –У–∞—Г—Б—Б–∞
 =>
=>
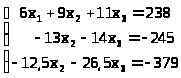 =>
=>
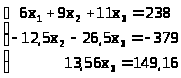 =>
=>
 =>
=>
 =>
=>
 =
>
=
>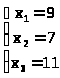
–Ч–∞–і–∞–љ–Є–µ 3
–Э–∞–є—В–Є —З–∞—Б—В–љ—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –њ–µ—А–≤–Њ–≥–Њ –Є –≤—В–Њ—А–Њ–≥–Њ –њ–Њ—А—П–і–Ї–Њ–≤ –Ј–∞–і–∞–љ–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є:

–†–µ—И–µ–љ–Є–µ:

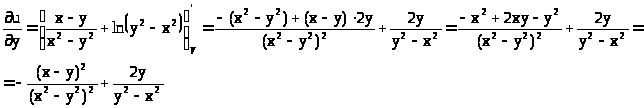

–Ч–∞–і–∞–љ–Є–µ 4
–Ч–∞–і–∞–љ–∞ —Д—Г–љ–Ї—Ж–Є—П
—Б–њ—А–Њ—Б–∞
 ,
–≥–і–µ p>1>, p>2>
- —Ж–µ–љ—Л –љ–∞ –њ–µ—А–≤—Л–є –Є –≤—В–Њ—А–Њ–є —В–Њ–≤–∞—А—Л
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ю—Б–љ–Њ–≤—Л–≤–∞—П—Б—М –љ–∞ —Б–≤–Њ–є—Б—В–≤–∞—Е
—Д—Г–љ–Ї—Ж–Є–Є —Б–њ—А–Њ—Б–∞, –Њ–њ—А–µ–і–µ–ї–Є—В—М: –Ї–∞–Ї–Њ–є —В–Њ–≤–∞—А
—П–≤–ї—П–µ—В—Б—П –Є—Б—Б–ї–µ–і—Г–µ–Љ—Л–Љ, –∞ –Ї–∞–Ї–Њ–є –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ—Л–Љ
–Є —Н–ї–∞—Б—В–Є—З–љ–Њ—Б—В—М —Б–њ—А–Њ—Б–∞ –њ–Њ —Ж–µ–љ–∞–Љ –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–≥–Њ
–Є –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–Њ–≥–Њ —В–Њ–≤–∞—А–Њ–≤. –Т –њ—А–Њ—Ж–µ—Б—Б–µ
—А–µ—И–µ–љ–Є—П –Њ—В–Љ–µ—В–Є—В—М, –Ї–∞–Ї–Є–Љ–Є —П–≤–ї—П—О—В—Б—П –і–∞–љ–љ—Л–µ
—В–Њ–≤–∞—А—Л - –≤–Ј–∞–Є–Љ–Њ–Ј–∞–Љ–µ–љ—П–µ–Љ—Л–Љ–Є –Є–ї–Є
–≤–Ј–∞–Є–Љ–Њ–і–Њ–њ–Њ–ї–љ—П–µ–Љ—Л–Љ–Є.
,
–≥–і–µ p>1>, p>2>
- —Ж–µ–љ—Л –љ–∞ –њ–µ—А–≤—Л–є –Є –≤—В–Њ—А–Њ–є —В–Њ–≤–∞—А—Л
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ю—Б–љ–Њ–≤—Л–≤–∞—П—Б—М –љ–∞ —Б–≤–Њ–є—Б—В–≤–∞—Е
—Д—Г–љ–Ї—Ж–Є–Є —Б–њ—А–Њ—Б–∞, –Њ–њ—А–µ–і–µ–ї–Є—В—М: –Ї–∞–Ї–Њ–є —В–Њ–≤–∞—А
—П–≤–ї—П–µ—В—Б—П –Є—Б—Б–ї–µ–і—Г–µ–Љ—Л–Љ, –∞ –Ї–∞–Ї–Њ–є –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ—Л–Љ
–Є —Н–ї–∞—Б—В–Є—З–љ–Њ—Б—В—М —Б–њ—А–Њ—Б–∞ –њ–Њ —Ж–µ–љ–∞–Љ –Є—Б—Б–ї–µ–і—Г–µ–Љ–Њ–≥–Њ
–Є –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ–Њ–≥–Њ —В–Њ–≤–∞—А–Њ–≤. –Т –њ—А–Њ—Ж–µ—Б—Б–µ
—А–µ—И–µ–љ–Є—П –Њ—В–Љ–µ—В–Є—В—М, –Ї–∞–Ї–Є–Љ–Є —П–≤–ї—П—О—В—Б—П –і–∞–љ–љ—Л–µ
—В–Њ–≤–∞—А—Л - –≤–Ј–∞–Є–Љ–Њ–Ј–∞–Љ–µ–љ—П–µ–Љ—Л–Љ–Є –Є–ї–Є
–≤–Ј–∞–Є–Љ–Њ–і–Њ–њ–Њ–ї–љ—П–µ–Љ—Л–Љ–Є.
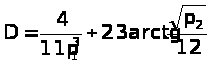
–†–µ—И–µ–љ–Є–µ: —Н–ї–∞—Б—В–Є—З–љ–Њ—Б—В—М —Б–њ—А–Њ—Б–∞ –њ–Њ —Ж–µ–љ–µ —А–∞–≤–љ–∞ –њ–µ—А–≤–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –Њ—В —Д—Г–љ–Ї—Ж–Є–Є —Б–њ—А–Њ—Б–∞:
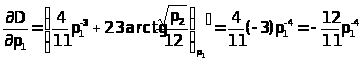
—Н–ї–∞—Б—В–Є—З–љ–Њ—Б—В—М –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–∞—П, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –њ–µ—А–≤—Л–є —В–Њ–≤–∞—А - –Є—Б—Б–ї–µ–і—Г–µ–Љ—Л–є.
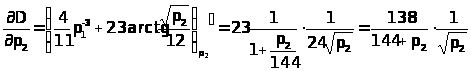
—Н–ї–∞—Б—В–Є—З–љ–Њ—Б—В—М –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ–∞—П, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –≤—В–Њ—А–Њ–є —В–Њ–≤–∞—А - –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ—Л–є.
–Ґ–Њ–≤–∞—А—Л —П–≤–ї—П—О—В—Б—П —В–Њ–≤–∞—А–∞–Љ–Є –Ј–∞–Љ–µ–љ–Є—В–µ–ї—П–Љ–Є, —В.–Ї —А–Њ—Б—В —Ж–µ–љ –љ–∞ –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ—Л–є —В–Њ–≤–∞—А –њ—А–Є–≤–Њ–і–Є—В –Ї —А–Њ—Б—В—Г —Б–њ—А–Њ—Б–∞.
–Ч–∞–і–∞–љ–Є–µ 5
–Т —В–∞–±–ї–Є—Ж–µ –њ—А–Є–≤–µ–і–µ–љ—Л –і–∞–љ–љ—Л–µ –Њ —В–Њ–≤–∞—А–Њ–Њ–±–Њ—А–Њ—В–µ –Љ–∞–≥–∞–Ј–Є–љ–∞ –Ј–∞ –њ—А–Њ—И–µ–і—И–Є–є –≥–Њ–і (–њ–Њ –Љ–µ—Б—П—Ж–∞–Љ). –Я—А–Њ–≤–µ—Б—В–Є –≤—Л—А–∞–≤–љ–Є–≤–∞–љ–Є–µ –і–∞–љ–љ—Л—Е –њ–Њ –њ—А—П–Љ–Њ–є —Б –њ–Њ–Љ–Њ—Й—М—О –Љ–µ—В–Њ–і–∞ –љ–∞–Є–Љ–µ–љ—М—И–Є—Е –Ї–≤–∞–і—А–∞—В–Њ–≤.
–Т–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–≤—И–Є—Б—М –љ–∞–є–і–µ–љ–љ—Л–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ –њ—А—П–Љ–Њ–є, —Б–і–µ–ї–∞—В—М –њ—А–Њ–≥–љ–Њ–Ј –Њ –≤–µ–ї–Є—З–Є–љ–µ —В–Њ–≤–∞—А–Њ–Њ–±–Њ—А–Њ—В–∞ —З–µ—А–µ–Ј –њ–Њ–ї–≥–Њ–і–∞ –Є –≥–Њ–і. –°–Њ–њ—А–Њ–≤–Њ–і–Є—В—М –Ј–∞–і–∞—З—Г —З–µ—А—В–µ–ґ–Њ–Љ, –љ–∞ –Ї–Њ—В–Њ—А–Њ–Љ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –њ–Њ—Б—В—А–Њ–Є—В—М –ї–Њ–Љ–∞–љ—Г—О —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Є—Е –і–∞–љ–љ—Л—Е –Є –њ–Њ–ї—Г—З–µ–љ–љ—Г—О –њ—А—П–Љ—Г—О.
–Я—А–Њ–∞–љ–∞–ї–Є–Ј–Є—А–Њ–≤–∞–≤ —З–µ—А—В–µ–ґ, —Б–і–µ–ї–∞–є—В–µ –≤—Л–≤–Њ–і—Л.
|
–Ь–µ—Б—П—Ж |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
–Ґ–Њ–≤–∞—А–Њ–Њ–±–Њ—А–Њ—В, (—В—Л—Б. —А) |
18 |
5,6 |
30,5 |
59,3 |
59,3 |
42 |
96,4 |
72,6 |
56,8 |
52 |
38,6 |
33 |
–†–µ—И–µ–љ–Є–µ:
–†–∞—Б—Б—З–Є—В–∞–µ–Љ –њ–∞—А–∞–Љ–µ—В—А—Л —Г—А–∞–≤–љ–µ–љ–Є—П –ї–Є–љ–µ–є–љ–Њ–є –њ–∞—А–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є.
–Ф–ї—П —А–∞—Б—З–µ—В–∞ –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ a –Є b —Г—А–∞–≤–љ–µ–љ–Є—П –ї–Є–љ–µ–є–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є —Г = –∞ + bx —А–µ—И–Є–Љ —Б–Є—Б—В–µ–Љ—Г –љ–Њ—А–Љ–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –∞ –Є b (–Њ–љ–∞ –≤—Л—В–µ–Ї–∞–µ—В –Є–Ј –Љ–µ—В–Њ–і–∞ –љ–∞–Є–Љ–µ–љ—М—И–Є—Е –Ї–≤–∞–і—А–∞—В–Њ–≤):

–Я–Њ –Є—Б—Е–Њ–і–љ—Л–Љ –і–∞–љ–љ—Л–Љ —А–∞—Б—Б—З–Є—В—Л–≤–∞–µ–Љ пБУ—Е, пБУ—Г, пБУ—Г—Е, пБУ—Е2, пБУ—Г2.
|
t |
y |
x |
yx |
x2 |
y2 |
|
|
1 |
18,0 |
1 |
18 |
1 |
324,00 |
33,662 |
|
2 |
5,6 |
2 |
11,2 |
4 |
31,36 |
36,089 |
|
3 |
30,5 |
3 |
91,5 |
9 |
930,25 |
38,516 |
|
4 |
59,3 |
4 |
237,2 |
16 |
3516,49 |
40,943 |
|
5 |
59,3 |
5 |
296,5 |
25 |
3516,49 |
43,37 |
|
6 |
42,0 |
6 |
252 |
36 |
1764,00 |
45,797 |
|
7 |
96,4 |
7 |
674,8 |
49 |
9292,96 |
48,224 |
|
8 |
72,6 |
8 |
580,8 |
64 |
5270,76 |
50,651 |
|
9 |
56,8 |
9 |
511,2 |
81 |
3226,24 |
53,078 |
|
10 |
52,0 |
10 |
520 |
100 |
2704,00 |
55,505 |
|
11 |
38,6 |
11 |
424,6 |
121 |
1489,96 |
57,932 |
|
12 |
33,0 |
12 |
396 |
144 |
1089,00 |
60,359 |
|
–Ш—В–Њ–≥–Њ |
564,1 |
78 |
4013,8 |
650 |
33155,51 |
564,13 |
 ;
;
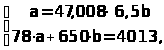 ;
;
 ;
;
 ;
;
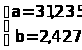
–£—А–∞–≤–љ–µ–љ–Є–µ —А–µ–≥—А–µ—Б—Б–Є–Є:
 =
31,235 + 2,427 ¬Ј —Е
=
31,235 + 2,427 ¬Ј —Е
–†–∞—Б—Б—З–Є—В–∞–µ–Љ
–њ–Њ –і–∞–љ–љ–Њ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є—О –Ј–љ–∞—З–µ–љ–Є—П –і–ї—П
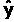 –Є –Ј–∞–њ–Є—И–µ–Љ –Є—Е –≤ –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–є —Б—В–Њ–ї–±–µ—Ж
–Є—Б—Е–Њ–і–љ—Л—Е –і–∞–љ–љ—Л—Е.
–Є –Ј–∞–њ–Є—И–µ–Љ –Є—Е –≤ –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–є —Б—В–Њ–ї–±–µ—Ж
–Є—Б—Е–Њ–і–љ—Л—Е –і–∞–љ–љ—Л—Е.
–Э–∞–є–і–µ–Љ –њ—А–Њ–≥–љ–Њ–Ј –љ–∞ –њ–Њ–ї–≥–Њ–і–∞ –≤–њ–µ—А–µ–і:
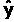 =
31,235 + 2,427 * 18 = 74,921 —В—Л—Б. —А—Г–±.
=
31,235 + 2,427 * 18 = 74,921 —В—Л—Б. —А—Г–±.
–Э–∞–є–і–µ–Љ –њ—А–Њ–≥–љ–Њ–Ј –љ–∞ –≥–Њ–і –≤–њ–µ—А–µ–і:
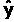 =
31,235 + 2,427 * 24 = 89,483 —В—Л—Б. —А—Г–±.
=
31,235 + 2,427 * 24 = 89,483 —В—Л—Б. —А—Г–±.
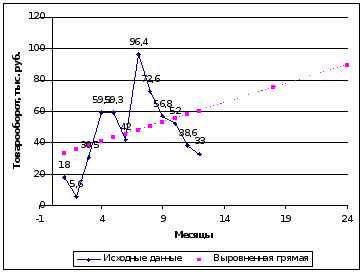
–Я–Њ–ї—Г—З–µ–љ–љ—Л–µ –≥—А–∞—Д–Є–Ї–Є –≥–Њ–≤–Њ—А—П—В –Њ –њ–ї–Њ—Е–Њ–Љ –Њ—В—А–∞–ґ–µ–љ–Є–Є –Є—Б—Е–Њ–і–љ—Л—Е –і–∞–љ–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ –њ—А—П–Љ–Њ–є. –Т–Њ–Ј–Љ–Њ–ґ–љ–Њ —Н—В–Њ —Б–≤—П–Ј–∞–љ–љ–Њ —Б –љ–∞–ї–Є—З–Є–µ–Љ —Б–µ–Ј–Њ–љ–љ–Њ—Б—В–Є –≤ —В–Њ–≤–∞—А–Њ–Њ–±–Њ—А–Њ—В–µ. –Ґ–Њ–≥–і–∞ –њ—А—П–Љ–∞—П –ї–Є–љ–Є—П —П–≤–ї—П–µ—В—Б—П —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ —В—А–µ–љ–і–∞.
–Ч–∞–і–∞–љ–Є–µ 6
–Ш—Б—Б–ї–µ–і–Њ–≤–∞—В—М –љ–∞ —Н–Ї—Б—В—А–µ–Љ—Г–Љ —Б–ї–µ–і—Г—О—Й—Г—О —Д—Г–љ–Ї—Ж–Є—О:
 ;
;
–†–µ—И–µ–љ–Є–µ:
–Э–∞–є–і–µ–Љ –њ–µ—А–≤—Л–µ —З–∞—Б—В–љ—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –Є –Њ–њ—А–µ–і–µ–ї–Є–Љ —В–Њ—З–Ї–Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Н–Ї—Б—В—А–µ–Љ—Г–Љ–Њ–≤.
 =
4x3 + 2xy2; 4x3
+ 2xy2 = 0; 2x (2x2
+ y2);
=
4x3 + 2xy2; 4x3
+ 2xy2 = 0; 2x (2x2
+ y2);
2x = 0 –Є–ї–Є (2x2 + y2) = 0; —В–Њ—З–Ї–∞ (0, 0)
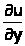 =
4y3 +
2x2y;
4y3 +
2x2y =
0; 2y (x2
+ 2y2);
=
4y3 +
2x2y;
4y3 +
2x2y =
0; 2y (x2
+ 2y2);
2y = 0 –Є–ї–Є (x2 + 2y2) = 0; —В–Њ—З–Ї–∞ (0, 0)
–Э–∞–є–і–µ–Љ –≤—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –Є –Є—Е –Ј–љ–∞—З–µ–љ–Є—П –≤ —В–Њ—З–Ї–µ (0; 0)
 =
12x2 +
2y2;
12 * 02
+ 2 * 02
= 0 = –Р
=
12x2 +
2y2;
12 * 02
+ 2 * 02
= 0 = –Р
 =
2xy; 2 * 0 * 0 = 0 = B
=
2xy; 2 * 0 * 0 = 0 = B
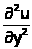 =
12y2 +
2x2;
12 * 02
+ 2 * 02
= 0 = C
=
12y2 +
2x2;
12 * 02
+ 2 * 02
= 0 = C
ќФ = AC - B2 = 0
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –≤–Њ–њ—А–Њ—Б –Њ–± —Н–Ї—Б—В—А–µ–Љ—Г–Љ–µ –Њ—Б—В–∞–µ—В—Б—П –Њ—В–Ї—А—Л—В—Л–Љ.
–Ґ–Њ—З–Ї–∞ (0; 0) –≤–Њ–Ј–Љ–Њ–ґ–љ—Л–є —Н–Ї—Б—В—А–µ–Љ—Г–Љ —Д—Г–љ–Ї—Ж–Є–Є.
–Ч–∞–і–∞—З–∞ 7
–Я—Г—Б—В—М —Д—Г–љ–Ї—Ж–Є—П –њ–Њ–ї–µ–Ј–љ–Њ—Б—В–Є –Ј–∞–і–∞–љ–∞ –Ї–∞–Ї

–≥–і–µ x –Є y - –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —В–Њ–≤–∞—А–Њ–≤ –Р –Є –Т, –њ—А–Є–Њ–±—А–µ—В–∞–µ–Љ—Л—Е –њ–Њ—В—А–µ–±–Є—В–µ–ї–µ–Љ, –∞ –Ј–љ–∞—З–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є –њ–Њ–ї–µ–Ј–љ–Њ—Б—В–Є —З–Є—Б–ї–µ–љ–љ–Њ –≤—Л—А–∞–ґ–∞—О—В –Љ–µ—А—Г —Г–і–Њ–≤–ї–µ—В–≤–Њ—А–µ–љ–Є—П –њ–Њ–Ї—Г–њ–∞—В–µ–ї—П. –Я—А–Є –і–∞–љ–љ–Њ–є —Б—В–Њ–Є–Љ–Њ—Б—В–Є –µ–і–Є–љ–Є—Ж—Л —В–Њ–≤–∞—А–Њ–≤ –Р –Є –Т, –Њ–±—Й–∞—П —Б—Г–Љ–Љ–∞, –≤—Л–і–µ–ї—П–µ–Љ–∞—П –њ–Њ–Ї—Г–њ–∞—В–µ–ї–µ–Љ –љ–∞ –Є—Е –њ–Њ–Ї—Г–њ–Ї—Г, —Б–Њ—Б—В–∞–≤–ї—П–µ—В 140 —А—Г–±–ї–µ–є. –Я—А–Є –Ї–∞–Ї–Њ–Љ –Ї–Њ–ї–Є—З–µ—Б—В–≤–µ —В–Њ–≤–∞—А–Њ–≤ –Р –Є –Т –њ–Њ–ї–µ–Ј–љ–Њ—Б—В—М –і–ї—П –њ–Њ—В—А–µ–±–Є—В–µ–ї—П –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–∞. –Р = 21, –Т = 37.
–†–µ—И–µ–љ–Є–µ: –њ–Њ–ї–µ–Ј–љ–Њ—Б—В—М –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–∞ –њ—А–Є —А–∞–≤–µ–љ—Б—В–≤–µ –њ–µ—А–≤—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е:
 =
=
 ;
;
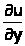 =
=
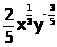 ;
;
 =
=
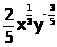 ;
;
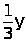 =
=
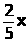
–Ю–≥—А–∞–љ–Є—З–µ–љ–Є–µ —Б—В–Њ–Є–Љ–Њ—Б—В–Є –Ј–∞–і–∞–µ—В—Б—П –љ–µ—А–∞–≤–µ–љ—Б—В–≤–Њ–Љ 21x + 37y вЙ§ 140
–°–Њ—Б—В–∞–≤–Є–Љ —Б–Є—Б—В–µ–Љ—Г.
 ;
;
 ;
;
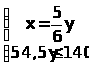 ;
;
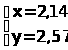
–Ь–∞–Ї—Б–Є–Љ–∞–ї—М–љ–∞—П –њ–Њ–ї–µ–Ј–љ–Њ—Б—В—М –±—Г–і–µ—В –і–Њ—Б—В–Є–≥–љ—Г—В–∞ –њ—А–Є –њ–Њ—В—А–µ–±–ї–µ–љ–Є–Є 2,14 –µ–і. –Р –Є 2,57 –µ–і.–≤.
–Ч–∞–і–∞–љ–Є–µ 8
–Ч–∞–і–∞–љ—Л —Д—Г–љ–Ї—Ж–Є–Є
—Б–њ—А–Њ—Б–∞ –Є –њ—А–µ–і–ї–Њ–ґ–µ–љ–Є—П –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В
–Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ —В–Њ–≤–∞—А–∞ Q:
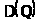 –Є
–Є
 .
–Я–Њ–і —Д—Г–љ–Ї—Ж–Є—П–Љ–Є —Б–њ—А–Њ—Б–∞ –Є –њ—А–µ–і–ї–Њ–ґ–µ–љ–Є—П
–±—Г–і–µ–Љ –њ–Њ–љ–Є–Љ–∞—В—М —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї—М–љ—Г—О –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М
—Ж–µ–љ—Л –Њ—В –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ —В–Њ–≤–∞—А–∞ –љ–∞ —А—Л–љ–Ї–µ.
–Ю–њ—А–µ–і–µ–ї–Є—В—М –Є–Ј–ї–Є—И–Ї–Є –њ–Њ—В—А–µ–±–Є—В–µ–ї—П –Є –Є–Ј–ї–Є—И–Ї–Є
–њ—А–Њ–Є–Ј–≤–Њ–і–Є—В–µ–ї—П –њ—А–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є
—Б–њ—А–Њ—Б–∞ –Є –њ—А–µ–і–ї–Њ–ґ–µ–љ–Є—П.
.
–Я–Њ–і —Д—Г–љ–Ї—Ж–Є—П–Љ–Є —Б–њ—А–Њ—Б–∞ –Є –њ—А–µ–і–ї–Њ–ґ–µ–љ–Є—П
–±—Г–і–µ–Љ –њ–Њ–љ–Є–Љ–∞—В—М —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї—М–љ—Г—О –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М
—Ж–µ–љ—Л –Њ—В –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ —В–Њ–≤–∞—А–∞ –љ–∞ —А—Л–љ–Ї–µ.
–Ю–њ—А–µ–і–µ–ї–Є—В—М –Є–Ј–ї–Є—И–Ї–Є –њ–Њ—В—А–µ–±–Є—В–µ–ї—П –Є –Є–Ј–ї–Є—И–Ї–Є
–њ—А–Њ–Є–Ј–≤–Њ–і–Є—В–µ–ї—П –њ—А–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є
—Б–њ—А–Њ—Б–∞ –Є –њ—А–µ–і–ї–Њ–ґ–µ–љ–Є—П.
 –Є
–Є
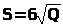 ,
,
–†–µ—И–µ–љ–Є–µ: –љ–∞–є–і–µ–Љ —А–∞–≤–љ–Њ–≤–µ—Б–љ–Њ–µ —Б–Њ—Б—В–Њ—П–љ–Є–µ —Б–њ—А–Њ—Б–∞ –Є –њ—А–µ–і–ї–Њ–ґ–µ–љ–Є—П:
D (Q)
= S (Q);
 =
=
 ;
;
 ;
-
;
-
 t2
- 6t + 300 = 0
t2
- 6t + 300 = 0
t>1> = - 25,12 –Є t>2> = 16,72, t>1> - –љ–µ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П–µ—В —Г—Б–ї–Њ–≤–Є—О
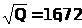 ;
Q = 279,56 –µ–і.
;
Q = 279,56 –µ–і.
–Я—А–Є —Н—В–Њ–Љ —Ж–µ–љ–∞ —Б–Њ—Б—В–∞–≤–Є—В: –† = 6 * 16,72 = 100,32 –і–µ–љ. –µ–і.
–Ш–Ј–ї–Є—И–Ї–Є –њ–Њ—В—А–µ–±–Є—В–µ–ї—П —А–∞–≤–љ—Л –њ–ї–Њ—Й–∞–і–Є —Д–Є–≥—Г—А—Л –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–є —Б–≤–µ—А—Е—Г –Ї—А–Є–≤–Њ–є —Б–њ—А–Њ—Б–∞, —Б–љ–Є–Ј—Г —А–∞–≤–љ–Њ–≤–µ—Б–љ–Њ–є —Ж–µ–љ–Њ–є –Є —Б–ї–µ–≤–∞ –љ—Г–ї–µ–≤—Л–Љ –≤—Л–њ—Г—Б–Ї–Њ–Љ. –Э–∞–є–і–µ–Љ –Є–Ј–ї–Є—И–Ї–Є –њ–Њ—В—А–µ–±–Є—В–µ–ї—П:
S>–њ–Њ—В—А> =
 -
100,32 ¬Ј 279,56 =
-
100,32 ¬Ј 279,56 =
 -
28045,46 =
-
28045,46 =
= 300 * 279,56 - 5/14 * 279,56 - 28045,46 = 55722,7
–Ш–Ј–ї–Є—И–Ї–Є –њ—А–Њ–Є–Ј–≤–Њ–і–Є—В–µ–ї—П —А–∞–≤–љ—Л –њ–ї–Њ—Й–∞–і–Є —Д–Є–≥—Г—А—Л –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–є —Б–≤–µ—А—Е—Г —А–∞–≤–љ–Њ–≤–µ—Б–љ–Њ–є —Ж–µ–љ–Њ–є, —Б–ї–µ–≤–∞ –љ—Г–ї–µ–≤—Л–Љ –≤—Л–њ—Г—Б–Ї–Њ–Љ –Є —Б–љ–Є–Ј—Г –Ї—А–Є–≤–Њ–є –њ—А–µ–і–ї–Њ–ґ–µ–љ–Є—П. –Э–∞–є–і–µ–Љ –Є–Ј–ї–Є—И–Ї–Є –њ—А–Њ–Є–Ј–≤–Њ–і–Є—В–µ–ї—П:
S>–њ—А–Њ–Є–Ј–≤>
= 100,32 ¬Ј 279,56 -
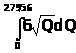 = 28045,46 -
= 28045,46 -
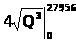 =
=
= 28045,46 - 4 * 16,723 = 9348,6
–Ы–Є—В–µ—А–∞—В—Г—А–∞
–Э.–®. –Ъ—А–µ–Љ–µ—А. –Т—Л—Б—И–∞—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ –і–ї—П —Н–Ї–Њ–љ–Њ–Љ–Є—Б—В–Њ–≤. - –Ь.: –С–∞–љ–Ї–Є –Є –±–Є—А–ґ–Є, –Ѓ–Э–Ш–Ґ–Ш, 1997.
–Э.–®. –Ъ—А–µ–Љ–µ—А. –Я—А–∞–Ї—В–Є–Ї—Г–Љ –њ–Њ –≤—Л—Б—И–µ–є –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ –і–ї—П —Н–Ї–Њ–љ–Њ–Љ–Є—Б—В–Њ–≤. - –Ь.: –Ѓ–Э–Ш–Ґ–Ш-–Ф–Р–Э–Р, 2007.
–Ш.–Р. –Ч–∞–є—Ж–µ–≤. –Т—Л—Б—И–∞—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞. - –Ь.: –Т—Л—Б—И–∞—П —И–Ї–Њ–ї–∞, 1998.
–Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–є –∞–љ–∞–ї–Є–Ј –Є –ї–Є–љ–µ–є–љ–∞—П –∞–ї–≥–µ–±—А–∞. –£—З–µ–±–љ–Њ–µ –Љ–µ—В–Њ–і–Є—З–µ—Б–Ї–Њ–µ –њ–Њ—Б–Њ–±–Є–µ. –Я–Њ–і —А–µ–і. –Э.–®. –Ъ—А–µ–Љ–µ—А–∞. - –Т–Ч–§–≠–Ш, 2006.