Расширение кольца с помощью полутела

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет

Математический факультет

Кафедра алгебры и геометрии

Выпускная квалификационная работа

Расширение кольца с помощью полутела

Выполнил:

студент V курса математического факультета

Лукин Михаил Александрович

_____________________

Научный руководитель:

д. ф.-м. н., профессор, зав. кафедрой алгебры и геометрии

Вечтомов Евгений Михайлович

_____________________

Рецензент:

к. ф.-м. н., доцент, доцент кафедры алгебры и геометрии

Чермных Василий Владимирович

_____________________

Допущен к защите в государственной аттестационной комиссии

«___» __________2005 г. Зав. кафедрой Е. М. Вечтомов

«___»___________2005 г. Декан факультета В. И. Варанкина

Киров – 2005

Содержание

Введение 3

§1. Допустимые кольца и решетки 6

§2. Допустимые полутела 10

§3. О единственности расширения 12

Заключение 14

Библиографический список 15

Введение

Теория полуколец является активно развивающимся разделом современной алгебры, находящим применения в компьютерной алгебре, идемпотентном анализе, теории оптимального управления.

Для получения новых конструкций полуколец может оказаться полезным понятие двойного расширения полуколец (или 0-1 расширения).

В работе исследуется следующий вопрос. Для каких кольца R, полутела U и ограниченной дистрибутивной решетки L существует 0-1-расширение кольца R и полутела U с помощью решетки L?

Полукольцом называется такая алгебраическая структура S; +, , 0, что S; +, 0 - коммутативный моноид с нулем 0, S,  - полугруппа и в S выполняются тождества a(b+c)=ab+ac, (a+b)c=ac+bc и a0=0a=0. Неодноэлементное полукольцо с делением, не являющееся кольцом, называется полутелом (с нулем). Если из полутела S исключить 0, то получим структуру S; +, , которую будем называть полутелом без нуля, или просто полутелом. Полукольцо с квазитождеством a+b=0  a=0 назовем антикольцом. Полукольцо с тождеством a+a=a называется идемпотентным. А полукольцо с квазитождеством a+b=a+c  b=c называется сократимым.

Полукольцо S назовем 0-расширением полукольца K с помощью полукольца T, если на S существует такая конгруэнция , что K[0]_>> - изоморфно нулевому ядру - и S/T. Аналогично, полукольцо S с единицей 1 называется 1-расширением полукольца K, возможно без нуля, с помощью полукольца T, если на S существует конгруэнция , для которой K[1]_>>_> >- изоморфно единичному ядру - и S/T. В отличие от колец данные расширения позволяют шире представлять сами полукольца, скажем, изучить симбиоз колец и полутел, или колец и антиколец (см. [1]).

Для произвольного полукольца S обозначим через R(S) множество всех аддитивно обратимых элементов в S, а через U(S) – множество всех обратимых элементов в S в случае, когда S обладает 1. Очевидно, что R(S) является кольцом и строгим идеалом полукольца S (т.е. a+bR(S)  a, bR(S)).

Пусть S/R(S) – фактор-полукольцо полукольца S по конгруэнции Берна, соответствующей идеалу R(S): s конгруэнтно t  s+a=t+b для некоторых a, bR(S). Положительное регулярное полукольцо, все идемпотенты которого центральны, называются arp-полукольцом [2]. При этом положительность полукольца S с 1 означает, что все элементы вида a+1, aS, обратимы, а его регулярность означает разрешимость в S каждого уравнения axa=a.

Справедливы следующие утверждения.

1. Любое полукольцо S является 0-расширением кольца, изоморфного R(S), с помощью положительно упорядоченного полукольца [1]

2. Полукольцо S с 1 изоморфно прямому произведению кольца и антикольца тогда и только тогда, когда его идеал R(S) имеет единичный элемент, коммутирующий с каждым элементом из S [1].

3. Полукольцо S служит 0-расширением кольца с помощью полутела тогда и только тогда, когда идеал R(S) полульца S простой (т.е. abR(S) влечет aR(S) или bR(S)).

4. Для полукольца S с 1 фактор-полукольцо S/R(S) является полутелом с нулем тогда и только, когда R(S) есть максимальный односторонний идеал в S.

В качестве следствия утверждений 2 и 4 очевидным образом формулируется критерий разложимости полукольца с 1 в прямое произведение кольца и полутела с нулем. Отметим также, что подпрямые произведения кольца и ограниченной дистрибутивной решетки абстрактно охарактеризованы в [3].

5. Для существования 1-расширения полукольца K, возможно не имеющего нуля, с помощью полукольца T необходимо и достаточно, чтобы K имело 1, а T было идемпотентным полукольцом с 1.

6. Любое arp-полукольцо S является 1-расширением полутела U(S) с помощью ограниченной дистрибутивной решетки S/, где  - конгруэнция на S, такая, что ab означает aU(S)=bU(S). Для коммутативных полуколец верно и обратное утверждение. См. [2].

7. Всякое полутело является 1-расширением сократимого полутела с помощью идемпотентного полутела [4].

Полукольцо S с 1 назовем 0-1-расширением полукольца K и полукольца без нуля L с помощью полукольца T, если на S существует такая конгруэнция , что [0]_>ρ>K, [1]_>>L и S/T.

Пусть для кольца R, полутела U и ограниченной дистрибутивной решетки L существует 0-1-расширение кольца R и полутела U с помощью решетки L. Соответствующую тройку <R ,P ,L> будем называть допустимой.

§1. Допустимые кольца и решётки

Речь в главе пойдёт о решётке и кольце, состоящих в допустимой тройке.

Обозначим через D двухэлементную цепь.

Пусть имеется полукольцо S с конгруэнцией , для которой [0]_>>R, [1]_>>P, F/D. Такое полукольцо S назовем дизъюнктным объединением кольца R и полутела P, и обозначим PR. Ясно, что pP,rR,prR,p+rP.

С другой стороны, если любой элемент полукольца S с 1 либо обратим, либо имеет противоположный элемент, то S будет дизъюнктным объединением кольца R(S) и полутела U(S). При этом разбиение {R(S), U(S)} индуцирует искомую конгруэнцию  на S.

Предложение. В UR справедливы следующие утверждения а) аддитивная группа R делимая абелева группа. б) результат умножения 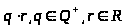определён единственным образом.

Доказательство. а) Пусть , тогда , ч.т.д.

б) Пусть мультипликативная операция задана. Если , то . Умножив равенство на справа, получим , значит . Рассмотрим результат умножения , пусть . Тогда , поэтому есть элемент, складывая который раз получим . Из ранее доказанного следует, что такой элемент единственен, что завершает доказательство. есть решение уравнения в кольце .

Теорема 1. Для произвольного кольца R эквивалентны следующие условия:

1. существует допустимая тройка R, U, L, где L – любая дистрибутивная решетка с 10;

   существует полукольцо, являющееся дизъюнктным объединением кольца R и полутела U;

   R – радикальное по Джекобсону кольцо, аддитивная группа которого есть делимая группа без кручения.

Доказательство.

12. Для данной тройки рассмотрим подходящие полукольцо S и конгруэнцию . Поскольку D - подрешетка дистрибутивной решетки L с 0 и 1, в качестве дизъюнктного объединения можно взять подполукольцо [1]_>>[0]_>> в S.

21. Любая дистрибутивная решетка L обладает простым идеалом I, более того L\I - дуальный идеал.

Поэтому в качестве полукольца S можно взять множество пар (i,r),iI,rR(l,p),lL/I,pP с покоординатным сложением и умножением. Ввиду простоты I операции заданы корректно, аксиомы полукольца выполняются, поскольку они выполняются для левой координаты, как аксиомы решётки и для правой координаты, что следует из существования F, [0]_>>R, [1]_>>P, F/L_>2>. Если в качестве конгруэнции  выбрать отношение равенства первых координат, то [0]_>>R, [1]_>>P, S/L_>2>, что завершает доказательство.

Лемма. Пусть в кольце R r r tR,(r+rr+r)t=0,(r+rr+r)t=0, тогда r r ,r+rr+r=0r+rr+r=0.

Доказательство. Пусть выполнено условие леммы, тогда, положим r=-r-rr. Имеем

r+rr+r = r+(- r - rr)r - r - rr = (r+rr+r)(-r)=0

r+rr+r = r+r (- r - rr) - r - rr = (r+rr+r)(-r)=0.

Кольцо R называется радикальным по Джекобсону, если оно совпадает со своим радикалом Джекобсона (см., например, [5]). Это означает, что операция «круговой композиции» rs = r+s+rs в R является групповой, с нейтральным элементом 0. Другими словами, в кольце R для любого элемента r существует единственный элемент s, такой, что r+s+rs=0.

2)3). P содержит Q⁺, иначе 1+1=1, умножив равенство на ненулевой элемент кольца r, имеем r+r=rr=0 – противоречие. Таким образом, R – полумодуль над Q⁺ и, значит, модуль над Q. Поэтому <R,+> - делимая абелева группа без кручения (подробно см. также предложение).

Множество T= Q⁺+R является подполутелом в U, поскольку

q_>1>+r_>1>+q_>2>+r_>2> _> >= (q_>1>+q_>2>)+(r_>1>+r_>2>);

(q_>1>+r_>1>)(q_>2>+r_>2>) = (q_>1>q_>2>+q_>1>r_>2>+r_>1>q_>2>+r_>1>r_>2>) = q_>1>q_>2>+(q_>1>r_>2>+r_>1>q_>2>+r_>1>r_>2>);

t=q+r1=qt ^-1+rt ^-1t ^-1=q ^-1- q ^-1r t ^-1 Q⁺ + R.

Следовательно, для любого элемента 1+r,rR найдётся, 1+r,rR что (1+r)(1+r) = (1+r)(1+r) = 1. Из дистрибутивности следует, что 1+r+rr+r = 1+r+rr+r = 1. Умножая последнее равенство на любое tR, имеем (r+rr+r)t=0(r+rr+r)t=0, значит, в виду леммы, R радикально по Джекобсону.

3)2). Поскольку R радикально по Джекобсону, алгебра Q⁺R с операциями

(q_>1>,r_>1>)+(q_>2>,r_>2>) _> >= (q_>1>+q_>2>)+(r_>1>+r_>2>), (q_>1>,r_>1>)(q_>2>,r_>2>) = (q_>1>q_>2>,q_>1>r_>2>+r_>1>q_>2>+r_>1>r_>2>)

является полутелом с единичным элементом (1,0). А множество S(Q⁺{0})R с теми же операциями совпадает с (Q⁺R)({0}R) = (Q⁺R)R.

Примеры. 1. Любое ниль-кольцо радикально по Джекобсону. В частности таково кольцо с нулевым умножением.

Ещё одним частным случаем является нильпотентное кольцо R, порождённое одним элементом .

Пусть  - образующий. Поскольку в качестве элементов R выступают p_>1> + p_>2>² + … + p_>n>_>-1>^n-1, p_>i>Q, n - наименьшая нулевая степень , T R - в точности совпадает с одним из двух полуколец.

(q+q_>1> + q_>2>² + … + q_>n>_>-1>^n-1,p_>1> + p_>2>² + … + p_>n>_>-1>^n-1)qQ⁺,q_>i>,p_>i>Q или

(q+q_>1> + q_>2>² + … + q_>n>_>-1>^n-2,p_>1> + p_>2>² + … + p_>n>_>-1>^n-1)qQ⁺,q_>i>,p_>i>Q

c операциями

(q_>1>,r_>1>)+(q_>2>,r_>2>) = (q_>1>+q_>2>)+(r_>1>+r_>2>), (q_>1>,r_>1>)(q_>2>,r_>2>) =  (q_>1>q_>2>,q_>1>r_>2>+r_>1>q_>2>+r_>1>r_>2>).

2. Радикальным по Джекобсону будет кольцо, совпадающее с подмножеством гипердействительных чисел R(0). Это коммутативное кольцо без делителей нуля. a(0), a+x+ax = 0x = (-a)/(1+a)(0)

Моделью представленного полукольца является прямое произведение двух подмножеств кольца Q[x]: многочленов с неотрицательным свободным членом и многочленов с положительным свободным членом. Множество пар, вида (q+q_>1> + q_>2>² + … + q_>n>_>-1>^l,p_>1> + p_>2>² + … + p_>n>_>-1>^m)qQ⁺,q_>i>,p_>i>

Соответственно частному функций задаются все операции в этом множестве (разумеется, берётся не всё множество пар, а множество классов факторполукольца, где две пары эквивалентны тогда и только тогда, когда равны произведения их противоположных координат).

Этот пример легко обобщается для многочленов от произвольного множества переменных.

§2. Допустимые полутела

Дальнейший ряд предложений направлен на отыскание всевозможных полутел P , что PR.

Замечания. 1. Пусть дано допустимое кольцо R, тогда множество элементов M = {mR, rR|r∙m = m∙r =0} образует в нём подкольцо.

2. Множество элементов E = {R,1+=1} образует в M и в R двусторонний идеал с делимой аддитивной группой.

3. Множество Q⁺×(R/I) является полутелом с операциями (q_>1>,r_>1>)+(q_>2>,r_>2>) = (q_>1>+q_>2>)+(r_>1>+r_>2>), (q_>1>,r_>1>)(q_>2>,r_>2>) = (q_>1>q_>2>,q_>1>r_>2>+r_>1>q_>2>+r_>1>r_>2>), где I - произвольный идеал с делимой аддитивной группой кольца R.

Теорема 2. Пусть R, U, D - допустимая тройка и R ненулевое. Тогда множество Q⁺+R есть подполутело U, изоморфное ((R/I)Q⁺), где I некоторый идеал аннулятора с делимой аддитивной группой. И существует канонический гомоморфизм  полутела U в кольцо R-модульных эндоморфизмов End _>R>R, образ которого содержит Q⁺. Если правый аннулятор кольца R нулевой, то полутело Im содержит подполутело, изоморфное ((R/I)Q⁺).

Доказательство. Пусть T, R - из допустимой тройки. Любой элемент T представим в виде q+r,qQ⁺,rR. Два элемента q+r_>1> и q+r_>2> равны тогда и только тогда, когда 1+r_>1>-r_>2>=1. С другой стороны, если 1+r = 1, то 1+r_>1>+r=1+r_>1>. Поэтому все элементы вида q+r+, 1+=1 сливаются в классы q×(R/I), где I - множество всех .

Отображение _>u>: RuR, uU ввиду дистрибутивности и ассоциативности в UR является R – модульным эндоморфизмом. Пусть _>u>+_>v>:R(u+v)R и _>u>_>v>:RuvR, тогда отображение : U End _>R>R, сопоставляющее каждому элементу uU эндоморфизм _>u> - канонический гомоморфизм.

Пусть правый аннулятор R нулевой, тогда для двух элементов q_>1>+r_>1>, q_>2>+r_>2>, считая без ограничения общности, q_>1>=q_>2>+q_>3 >(q_>3> может равняться нулю), r, (q_>1>+r_>1>)r=(q_>2>+r_>2>)r(q_>3>+r_>1>-r_>2>)r=0q_>3>=0,r_>1>=r_>2>. Элементы q_>1>+r_>1> и q_>2>+r_>2> одинаково действуют на R только в случае равенства. Поэтому  - мономорфизм и Im содержит подполутело, изоморфное ((R/I)Q⁺).

Замечание. Система (Q⁺×(R/I))({0}×R) с операциями (q_>1>,r_>1>)+(q_>2>,r_>2>) = (q_>1>+q_>2>)+(r_>1>+r_>2>), (q_>1>,r_>1>)(q_>2>,r_>2>) = (q_>1>q_>2>,q_>1>r_>2>+r_>1>q_>2>+r_>1>r_>2>) и произвольным идеалом аннулятора с делимой аддитивной группой I является дизъюнктным объединением. Сложение класса (R/I) с элементом кольца определяется как сложение любого элемента этого класса с элементом кольца.

§3. О единственности расширения

При изучении структуры дизъюнктных объединений кольца и полутела возникает вопрос о единственности UR для данных U и R. Ниже приведём пример существования несовпадающих дизъюнктных объединений при заданных U и R.

Пусть для данных полутела U и кольца R существует коммутативное U_> >R и пусть tR не лежит в AnnR, но trAnnRrR (примером такого дизъюнктного объединения с элементом t служит

(q+q_>1> + q_>2>² + … + q_>n>_>-1>^n-1,p_>1> + p_>2>² + … + p_>n>_>-1>^n-1)qQ⁺,q_>i>,p_>i>Q из примера 1).

Определим новые операции на UR следующим образом: Умножение оставим неизменным, а сложение элементов rR и uU сложение зададим законом ur=u+r+rt. Поскольку операции внутри полутела и кольца при этом не меняются, достаточно проверить выполнение законов:

1. Ассоциативность сложения:

(u_>1>u_>2>)r=u_>1>(u_>2>r)u_>1>+u_>2>+r+rt= u_>1>+u_>2>+r+rt

(ur_>1>)r_>2>=u(r_>1>r_>2>)u+r_>1>+r_>1>t+r_>2>+r_>2>t=u+r_>1>+r_>2>+(r_>1>+r_>2>)t.

2. Дистрибутивность:

u_>1>(ru_>2>)=u_>1>ru_>1>u_>2>u_>1>(r+u_>2>+rt)=u_>1>u_>2>+u_>1>r+u_>1>rt

r_>1>(ur_>2>)=r_>1>ur_>1>r_>2>r_>1>u+r_>1>r_>2>+r_>1>r_>2>t=r_>1>u+r_>1>r_>2>.

Таким образом, UR с новыми операциями является дизъюнктным объединением. Однако, два имеющихся полукольца изоморфны между собой, поскольку существует изоморфизм f:uuuU:

r(1+t)^-1rrR. Причём f_>t> :r(1+t)^-1rrR – автоморфизм R.

Доказательство. Имеем f_>t> – автоморфизм R, поскольку для каждого элемента r имеется свой праобраз (1+t)r. И выполняются тождества

r_>1>,r_>2>, f_>t>(r_>1>+r_>2>)=(1+t)^-1(r_>1>+r_>2>)= (1+t)^-1r_>1>+(1+t)^-1r_>2>=f_>t>(r_>1>)+ f_>t>(r_>2>)

r_>1>,r_>2>,(1+t)^-1(r_>1>∙r_>2>)=(1+t)^-1(1+t)^-1(r_>1>∙r_>2>),

поскольку (1+t)r_>1>r_>2>=r_>1>r_>2>. Поэтому в виду коммутативности полукольца f_>t>(r_>1>∙r_>2>)= f_>t>(r_>1>)f_>t> (r_>2>).

Поскольку при отображении f кольцо и полутело автоморфно переходят в себя, изоморфизм полуколец вытекает из следующих тождеств:

uU, rR f(u+r)=u+r= u+r+(1+t)^-1r f(u)f(r)

uU, rR f(ur)=(1+t)^-1ur=u(1+t)^-1r=f(u) f(r).

Вопрос о том, единственным ли является дизъюнктное объединение с точностью до изоморфизма остаётся открытым.

Заключение

В дипломной работе представлено описание 0-1-расширений кольца R и полутела U с помощью решетки L. Установлены, следующие факты:

существование 0-1-расширения не зависит от строения дистрибутивной решётки L (теорема 1);

кольцо R состоит в какой либо допустимой тройке тогда и только тогда, когда оно радикально по Джекобсону (теорема 1);

строение полутела U существенно зависит от строения R (теорема 2).

Не решённым остаётся вопрос о единственности с точностью до изоморфизма UR. В работе устанавливается взаимосвязь между значимыми математическими структурами - кольцами и полутелами. Подобные взаимосвязи могут существовать и между другими объектами алгебры, существенным может оказаться изучение и обобщение таких взаимосвязей.

Библиографический список

Вечтомов Е.М. Две общие структурные теоремы о полумодулях // Абелевы группы и модули: сб. статей / Под ред. А.В. Михалева. Вып. 15. –Томск: ТГУ, 2000. – С. 17-23.

Вечтомов Е.М., Михалев А.В., Чермных В.В. Абелево-регурярные положительные полукольца // Труды семинара им. И.Г. Петровского. – 2000. – Т 20. – С. 282-309.

Golan J.S. The theory of semirings with applications in mathematics and theoretical computer science // Pitman monographs and surveys in pure and applied mathematics. V. 54. – 1992. – S. 93-98.

Семенов А.Н. О строении полутел // Вестник ВятГГУ. – 2003. – № 8. – С. 105-107.

Херстейн И. Некоммутативные кольца. – М.: Мир, 1972. – 200 с.

1