Математическое моделирование в задачах расчета и проектирования систем автоматического управления
Московский государственный технический университет им. Н.Э. Баумана
Калужский филиал
Кафедра “САУ и Электротехники”
ЭИУ3-КФ
Расчётно-пояснительная записка к курсовой работе
на тему:
“ МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ЗАДАЧАХ РАСЧЕТА И ПРОЕКТИРОВАНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ”
по курсу:
Системы аналитических вычислений
Калуга
Содержание
1 Постановка задачи
2 Анализ устойчивости
3 Решение дифференциального уравнения интерполяционным методом Адамса
4 Синтез
Вывод
Список литературы
Приложение 1 (Листинг скрипта для нахождения корней полинома)
Приложение 2 (Листинг скрипта для решения дифференциального уравнения
численным методом)
Приложение 3 (Листинг скриптов для нахождения коэффициентов регулятора)
1 Постановка задачи
Требуется:
1. Выполнить анализ устойчивости работы нескорректированной системы управления.
2. Выполнить анализ функционирования системы
3. Синтезировать регулятор для системы управления.
4. Выполнить анализ работы скорректированной системы управления.
Структурная схема системы приведена на рис. 1.
Рис.
1. Структурная схема контура стабилизации
угла тангажа
Параметры системы имеют следующие значения:
Требования к системе:
2 Анализ устойчивости
Выполним анализ нескорректированной системы с использованием критериев Михайлова и Гурвица.
Найдем передаточную функцию всей системы
Составим матрицу Гурвица
a>0>=1; a>1>=7.4; a>2>=19; a>3>=10;
По критерию Гурвица для того,
чтобы система была устойчива необходимо
и достаточно, чтобы все определители
на главной диагонали были больше нуля
Найдем все миноры на главной диагонали:
Система
устойчива.
Критерий Михайлова:
Из условия
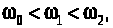Получаем, что система устойчива.
Построим годограф разомкнутой системы и найдем запас устойчивости.
На рис. 2 приведен график АФЧХ разомкнутой системы и единичная окружность.
Рис. 2.Годограф АФЧХ разомкнутой системы
По рис. 2 легко определить запас устойчивости замкнутой системы.
Нахождение корней характеристического уравнения методом градиентов.
Найдем корни передаточной функции с помощью метода градиентов.
Рабочая формула используемого метода имеет следующий вид
где
и
векторы неизвестных на шаге k+1
и k.
- транспонированная матрица
Якоби, вычисленная на шаге k.
Невязка на шаге k
Шаговый множитель
Находим полюса для передаточной функции, имеющий вид
Текст программы приведен в приложении 1.
Результат приведен на рис.3
Рис. 3. Пример нахождения полюсов ПФ W(s)
Аналитические выражения для переходной и импульсной переходной функций, АЧХ, ФЧХ, АФЧХ
Найдем импульсную переходную функцию.
График k(t) приведен на рис. 4.
Рис. 4. График импульсной переходной функции.
Найдем переходную функцию.
График h(t) приведен на рис. 5.
Рис. 5. График переходной функции.
Найдем амплитудно-частотную характеристику.
График АЧХ приведен на рис. 6.
Рис. 6. График АЧХ
Найдем ФЧХ:
График ФЧХ приведен на рис. 7.
>
>
Рис. 7. График ФЧХ
Найдем АФЧХ.
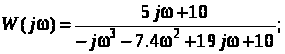
График ФЧХ приведен на рис. 8.
Рис. 8. График АФЧХ
Вывод: Система является устойчивой, перерегулирование равно 0, время управления примерно равно 5с.
3 Решение дифференциального уравнения интерполяционным методом Адамса
Так как ДУ заданной системы имеет третий порядок, то его необходимо свести к системе уравнений, каждое из которых должно иметь первый порядок, т.е. имеет место нормальная форма Коши:
Запишем нормальную форму Коши в следующем виде:
Приведём уравнение к нормальной форме Коши:
Интерполяционный метод Адамса 3:
,
точность
Для того, чтобы использовать
этот неявный метод, нужно знать
Получим
методом Эйлера:
точность
Для получения точности
на первом шаге, возьмем
Текст программы находится в приложении 2.
Результаты работы программы при h равных 0.5, 0.2, 0.01 приведены на рис. 9.
>
>
Рис. 9. Отклики на единичное ступенчатое воздействие
4 Синтез
Введем в прямую цепь ПИД регулятор, а в обратную ПД.
Вид скорректированной системы приведен на рис. 10.
Рис.10. Структурная схема скорректированной системы
Найдем передаточную функцию системы
Передаточная функция разомкнутой цепи имеет вид:
Передаточная функция разомкнутой цепи имеет вид:
Для решения задачи синтеза необходимо найти параметра регулятора, при которых реальный выходной сигнал, являющийся реакцией на единичное ступенчатое воздействие, будет близок к заданному эталонному сигналу.
В качестве эталонного выходного сигнала используем следующий сигнал:
,
Коэффициент находим по следующей формуле:
Найдем параметры регулятора методом квадратичной аппроксимации.
Рабочая формула метода имеет вид:
Где,
градиент функции.
матрица Гессе функции
находим с помощью метода Золотого
сечения.
Текст программы находится в приложении 3.
Результат работы программы приведен на рис. 11.
>
>
Рис. 11. Пример получения коэффициентов регулятора.
Переходная функция скорректированной системы изображена на рис. 12.
Время управления скорректированной системы исходя из графика примерно равно 2.4с.
>
>
Рис. 12. Сравнение эталонной и реальной переходных функций
Вывод
В данной курсовой работе был синтезирован регулятор САУ, найдены его параметры численным методом. Также было решено дифференциальное уравнение неявным численным методом.
Список литературы
1. Методы классической и современной теории автоматического управления: Учебник в 5-ти т.; 2-е изд., перераб. и доп. Т.3: Синтез регуляторов систем автоматического управления / Под редакцией К.А. Пупкова и Н.Д. Егупова. – М.: Издательство МГТУ им. Н.Э. Баумана, 2004. – 616с.; ил.
2. Н.Д. Егупов, Ю.П. Корнюшин, Ю.И. Мышляев. Учебное пособие по выполнению курсового проектирования по дисциплине «Системы аналитических вычислений» для студентов специальности 160403 «Системы управления летательными аппаратами»
Приложение 1
Метод градиентов
function M_Gradientov
clc
% Решим уравнение s^3+7,4*s^2+19*s+10=0
e=10^-4;
s=0;
A1=1;
A2=7.4;
A3=19;
A4=10;
r0=1;
i=0; %количество итераций
while abs(r0)>e
i=i+1;
s0=s;
r0=A1*s^3+A2*s^2+A3*s+A4; %невязка
Ar=(A1+A2+A3)*r0;
AAr=(A1^2+A2^2+A3^3)*r0;
m=r0*AAr/AAr^2;
s=s0-m*Ar;
end
S1=s; % Нашли вешественный корень
Теперь решаем уранение: A1*s^2+(A2+A1*S1)*s+(A3+A2*S1+A1*s^2)=0
% Корни комплексные
D=(A2+A1*S1)^2-4*A1*(A3+A2*S1+A1*s^2);
S2=(-(A2+A1*S1)+sqrt(D))/2*A1;
S3=(-(A2+A1*S1)-sqrt(D))/2*A1;
disp(S1);
disp(S2);
disp(S3);
disp('Количество итераций'); disp(i);
Приложение 2
Интерполяционный метод Адамса
function Int_Adams_3
clc
%время переходного процесса
T=10;
%-----------------%
%матрица А (X'=AX+BY)
A=[0 1 0;
0 0 1;
-10 -19 -7.4];
%матрица B
B=[0 5 10]';
Y=[0 0 1]';
k=1;
%начальные условия
X(1,1:3)=[0 0 0];
I=[1 0 0; 0 1 0; 0 0 1];
while(k<=3)
%шаг
if(k==1) h=0.1; end;
if(k==2) h=1; end;
if(k==3) h=0.01; end;
%---------------------------%
n=1;
F(1,1:3)=(A*(X(1,1:3))'+B.*Y)';
X(n+1,1:3)=(X(n,1:3)'+h/10*(F(n,1:3))')';% Метод Эйлера
n=n+1;
while (n<=T/h)
F(n,1:3)=(A*(X(n,1:3))'+B.*Y)';
X(n+1,1:3)=(((I-5*h/12*A)^-1)*(X(n,1:3)'+h/12*(5*B.*Y+8*(F(n,1:3))'-(F(n-1,1:3))')))';
n=n+1;
end
t=0:h:10;
%k=t/h+1;
i=1;
while(i<=n)
if(k==1) t1=t; x1(i)=X(i,1); Xa1=1-0.9202*exp(-0.6983*t)-0.4636*exp(-3.3508*t).*cos(1.7584*t+4.382)+0.2433*exp(-3.3508*t).*sin(1.7584*t+4.382); end;
if(k==2) t2=t; x2(i)=X(i,1); Xa2=1-0.9202*exp(-0.6983*t)-0.4636*exp(-3.3508*t).*cos(1.7584*t+4.382)+0.2433*exp(-3.3508*t).*sin(1.7584*t+4.382); end;
if(k==3) t3=t; x3(i)=X(i,1); Xa3=1-0.9202*exp(-0.6983*t)-0.4636*exp(-3.3508*t).*cos(1.7584*t+4.382)+0.2433*exp(-3.3508*t).*sin(1.7584*t+4.382);
end;
i=i+1;
end
k=k+1;
end
t=0:0.01:10;
Xa=1-0.9202*exp(-0.6983*t)-0.4636*exp(-3.3508*t).*cos(1.7584*t+4.382)+0.2433*exp(-3.3508*t).*sin(1.7584*t+4.382);
plot(t,Xa,t1,x1,t1,(Xa1-x1),t2,x2,t2,(Xa2-x2),t3,x3,t3,(Xa3-x3)),grid on
Приложение3
Оптимизация методом квадратичной аппроксимации
function minK
%зададим точность и шаг
eps=0.1;
h=0.1;
%определим матрицу K=[Kp,Kd,Ki,Kp2,Kd2]';
T=4;
K0=[26 6 50 1 0.2]';
%Найдем J0
J0=Xr5(26, 6, 50, 1 ,0.2,T);
%------------------------
%Ищем матрицу G
a=Xr5(K0(1),K0(2),K0(3),K0(4),K0(5),T);
g11=(Xr5(K0(1)+2*h,K0(2),K0(3),K0(4),K0(5),T)-2*Xr5(K0(1)+h,K0(2),K0(3),K0(4),K0(5),T)+a)/h^2;
g12=(Xr5(K0(1)+h,K0(2)+h,K0(3),K0(4),K0(5),T)-Xr5(K0(1)+h,K0(2),K0(3),K0(4),K0(5),T)-Xr5(K0(1),K0(2)+h,K0(3),K0(4),K0(5),T)+a)/h^2;
g21=g12;
g13=(Xr5(K0(1)+h,K0(2),K0(3)+h,K0(4),K0(5),T)-Xr5(K0(1)+h,K0(2),K0(3),K0(4),K0(5),T)-Xr5(K0(1),K0(2),K0(3)+h,K0(4),K0(5),T)+a)/h^2;
g31=g13;
g14=(Xr5(K0(1)+h,K0(2),K0(3),K0(4)+h,K0(5),T)-Xr5(K0(1)+h,K0(2),K0(3),K0(4),K0(5),T)-Xr5(K0(1),K0(2),K0(3),K0(4)+h,K0(5),T)+a)/h^2;
g41=g14;
g15=(Xr5(K0(1)+h,K0(2),K0(3),K0(4),K0(5)+h,T)-Xr5(K0(1)+h,K0(2),K0(3),K0(4),K0(5),T)-Xr5(K0(1),K0(2),K0(3),K0(4),K0(5)+h,T)+a)/h^2;
g51=g15;
g22=(Xr5(K0(1),K0(2)+2*h,K0(3),K0(4),K0(5),T)-2*Xr5(K0(1),K0(2)+h,K0(3),K0(4),K0(5),T)+a)/h^2;
g23=(Xr5(K0(1),K0(2)+h,K0(3)+h,K0(4),K0(5),T)-Xr5(K0(1),K0(2)+h,K0(3),K0(4),K0(5),T)-Xr5(K0(1),K0(2),K0(3)+h,K0(4),K0(5),T)+a)/h^2;
g32=g23;
g24=(Xr5(K0(1),K0(2)+h,K0(3),K0(4)+h,K0(5),T)-Xr5(K0(1),K0(2)+h,K0(3),K0(4),K0(5),T)-Xr5(K0(1),K0(2),K0(3),K0(4)+h,K0(5),T)+a)/h^2;
g42=g24;
g25=(Xr5(K0(1),K0(2)+h,K0(3),K0(4),K0(5)+h,T)-Xr5(K0(1),K0(2)+h,K0(3),K0(4),K0(5),T)-Xr5(K0(1),K0(2),K0(3),K0(4),K0(5)+h,T)+a)/h^2;
g52=g25;
g33=(Xr5(K0(1),K0(2),K0(3)+2*h,K0(4),K0(5),T)-2*Xr5(K0(1),K0(2),K0(3)+h,K0(4),K0(5),T)+a)/h^2;
g34=(Xr5(K0(1),K0(2),K0(3)+h,K0(4)+h,K0(5),T)-Xr5(K0(1),K0(2),K0(3)+h,K0(4),K0(5),T)-Xr5(K0(1),K0(2),K0(3),K0(4)+h,K0(5),T)+a)/h^2;
g43=g34;
g35=(Xr5(K0(1),K0(2),K0(3)+h,K0(4),K0(5)+h,T)-Xr5(K0(1),K0(2),K0(3)+h,K0(4),K0(5),T)-Xr5(K0(1),K0(2),K0(3),K0(4),K0(5)+h,T)+a)/h^2;
g53=g35;
g44=(Xr5(K0(1),K0(2),K0(3),K0(4)+2*h,K0(5),T)-2*Xr5(K0(1),K0(2),K0(3),K0(4)+h,K0(5),T)+a)/h^2;
g45=(Xr5(K0(1),K0(2),K0(3),K0(4)+h,K0(5)+h,T)-Xr5(K0(1),K0(2),K0(3),K0(4)+h,K0(5),T)-Xr5(K0(1),K0(2),K0(3),K0(4),K0(5)+h,T)+a)/h^2;
g54=g45;
g55=(Xr5(K0(1),K0(2),K0(3),K0(4),K0(5)+2*h,T)-2*Xr5(K0(1),K0(2),K0(3),K0(4),K0(5)+h,T)+a)/h^2;
G=[g11, g12, g13, g14, g15; g21, g22, g23, g24, g25; g31, g32 ,g33, g34, g35; g41, g42 ,g43, g44, g45; g51, g52 ,g53, g54, g55;];
%G1=G.^-1;
G1=inv(G);
%построим градиент
gr1=(Xr5(K0(1)+h,K0(2),K0(3),K0(4),K0(5), T)-a)/h;
gr2=(Xr5(K0(1),K0(2)+h,K0(3),K0(4),K0(5), T)-a)/h;
gr3=(Xr5(K0(1),K0(2),K0(3)+h,K0(4),K0(5), T)-a)/h;
gr4=(Xr5(K0(1),K0(2),K0(3),K0(4)+h,K0(5), T)-a)/h;
gr5=(Xr5(K0(1),K0(2),K0(3),K0(4),K0(5)+h, T)-a)/h;
grad=[gr1 gr2 gr3 gr4 gr5]';
L=lambdamin(K0,G1,grad);
K=K0+L*G1*grad;
G10=G1;
grad0=grad;
J=Xr5(K(1),K(2),K(3),K(4),K(5),T);
% квадратичная аппроксимация: X(i+1)=X(i)-L(i)G^-1(i)GRAD(x(i))
while (J0>J)
J0=J;
%Ищем матрицу G
a=Xr5(K(1),K(2),K(3),K(4),K(5),T);
g11=(Xr5(K(1)+2*h,K(2),K(3),K(4),K(5),T)-2*Xr5(K(1)+h,K(2),K(3),K(4),K(5),T)+a)/h^2;
g12=(Xr5(K(1)+h,K(2)+h,K(3),K(4),K(5),T)-Xr5(K(1)+h,K(2),K(3),K(4),K(5),T)-Xr5(K(1),K(2)+h,K(3),K(4),K(5),T)+a)/h^2;
g21=g12;
g13=(Xr5(K(1)+h,K(2),K(3)+h,K(4),K(5),T)-Xr5(K(1)+h,K(2),K(3),K(4),K(5),T)-Xr5(K(1),K(2),K(3)+h,K(4),K(5),T)+a)/h^2;
g31=g13;
g14=(Xr5(K(1)+h,K(2),K(3),K(4)+h,K(5),T)-Xr5(K(1)+h,K(2),K(3),K(4),K(5),T)-Xr5(K(1),K(2),K(3),K(4)+h,K(5),T)+a)/h^2;
g41=g14;
g15=(Xr5(K(1)+h,K(2),K(3),K(4),K(5)+h,T)-Xr5(K(1)+h,K(2),K(3),K(4),K(5),T)-Xr5(K(1),K(2),K(3),K(4),K(5)+h,T)+a)/h^2;
g51=g15;
g22=(Xr5(K(1),K(2)+2*h,K(3),K(4),K(5),T)-2*Xr5(K(1),K(2)+h,K(3),K(4),K(5),T)+a)/h^2;
g23=(Xr5(K(1),K(2)+h,K(3)+h,K(4),K(5),T)-Xr5(K(1),K(2)+h,K(3),K(4),K(5),T)-Xr5(K(1),K(2),K(3)+h,K(4),K(5),T)+a)/h^2;
g32=g23;
g24=(Xr5(K(1),K(2)+h,K(3),K(4)+h,K(5),T)-Xr5(K(1),K(2)+h,K(3),K(4),K(5),T)-Xr5(K(1),K(2),K(3),K(4)+h,K(5),T)+a)/h^2;
g42=g24;
g25=(Xr5(K(1),K(2)+h,K(3),K(4),K(5)+h,T)-Xr5(K(1),K(2)+h,K(3),K(4),K(5),T)-Xr5(K(1),K(2),K(3),K(4),K(5)+h,T)+a)/h^2;
g52=g25;
g33=(Xr5(K(1),K(2),K(3)+2*h,K(4),K(5),T)-2*Xr5(K(1),K(2),K(3)+h,K(4),K(5),T)+a)/h^2;
g34=(Xr5(K(1),K(2),K(3)+h,K(4)+h,K(5),T)-Xr5(K(1),K(2),K(3)+h,K(4),K(5),T)-Xr5(K(1),K(2),K(3),K(4)+h,K(5),T)+a)/h^2;
g43=g34;
g35=(Xr5(K(1),K(2),K(3)+h,K(4),K(5)+h,T)-Xr5(K(1),K(2),K(3)+h,K(4),K(5),T)-Xr5(K(1),K(2),K(3),K(4),K(5)+h,T)+a)/h^2;
g53=g35;
g44=(Xr5(K(1),K(2),K(3),K(4)+2*h,K(5),T)-2*Xr5(K(1),K(2),K(3),K(4)+h,K(5),T)+a)/h^2;
g45=(Xr5(K(1),K(2),K(3),K(4)+h,K(5)+h,T)-Xr5(K(1),K(2),K(3),K(4)+h,K(5),T)-Xr5(K(1),K(2),K(3),K(4),K(5)+h,T)+a)/h^2;
g54=g45;
g55=(Xr5(K(1),K(2),K(3),K(4),K(5)+2*h,T)-2*Xr5(K(1),K(2),K(3),K(4),K(5)+h,T)+a)/h^2;
G=[g11, g12, g13, g14, g15; g21, g22, g23, g24, g25; g31, g32 ,g33, g34, g35; g41, g42 ,g43, g44, g45; g51, g52 ,g53, g54, g55;];
%G1=G.^-1;
G1=inv(G);
%построение градиента
gr1=(Xr5(K(1)+h,K(2),K(3),K(4),K(5), T)-a)/h;
gr2=(Xr5(K(1),K(2)+h,K(3),K(4),K(5), T)-a)/h;
gr3=(Xr5(K(1),K(2),K(3)+h,K(4),K(5), T)-a)/h;
gr4=(Xr5(K(1),K(2),K(3),K(4)+h,K(5), T)-a)/h;
gr5=(Xr5(K(1),K(2),K(3),K(4),K(5)+h, T)-a)/h;
grad=[gr1 gr2 gr3 gr4 gr5]';
if(Xr5(K(1),K(2),K(3),K(4),K(5),T)>Xr5(K0(1),K0(2),K0(3),K0(4),K0(5),T))
L=lambdamin(K0,G10,grad0);
end
K0=K;
G10=G1;
grad0=grad;
K=K0+L*G1*grad;
J=Xr5(K(1),K(2),K(3),K(4),K(5),T);
end
disp(K0);
disp(J0);
Метод Золотого Сечения
function L=lambdamin(K,G1,grad)
Xzs=(-1+sqrt(5))/2; %золотое сечение
a=0;
b=1;
while (abs(b-a) >0.01)
x1=a+(b-a)*Xzs;
x2=b-(b-a)*Xzs;
F1=K-x1*G1*grad;
F2=K-x2*G1*grad;
if ((x1 < x2)&&(Xr5(F1(1),F1(2),F1(3),F1(4),F1(5),2) <= Xr5(F2(1),F2(2),F2(3),F2(4),F2(5),2)))
b=x2;
end
if ((x1 > x2)&&(Xr5(F1(1),F1(2),F1(3),F1(4),F1(5),2) <= Xr5(F2(1),F2(2),F2(3),F2(4),F2(5),2)))
a=x2;
end
if ((x1 < x2)&&(Xr5(F1(1),F1(2),F1(3),F1(4),F1(5),2) > Xr5(F2(1),F2(2),F2(3),F2(4),F2(5),2)))
a=x1;
end
if ((x1 > x2)&&(Xr5(F1(1),F1(2),F1(3),F1(4),F1(5),2) > Xr5(F2(1),F2(2),F2(3),F2(4),F2(5),2)))
b=x1;
end
end
L=abs((x2-x1)/2);
Построение эталонного и реального выходного сигнала, поиск значения функционала.
function J=Xr5(Kp,Kd,Ki,Kp2,Kd2,t)
%коэффициенты ДУ
a4=1;
a3=(7.4+5*Kd*Kp2+5*Kp*Kd2+10*Kd*Kd2)/(1+5*Kd*Kd2);
a2=(14+5*Kp*Kp2+10*Kp2*Kd+10*Kd2*Kp+5*Ki*Kd2)/(1+5*Kd*Kd2);
a1=(10*Kp*Kp2+10*Ki*Kd2+5*Kp2*Ki)/(1+5*Kd*Kd2);
a0=(10*Ki*Kp2)/(1+5*Kd*Kd2);
b3=5*Kd/(1+5*Kd*Kd2);
b2=(5*Kp+10*Kd)/(1+5*Kd*Kd2);
b1=(10*Kp+5*Ki)/(1+5*Kd*Kd2);
b0=10*Ki/(1+5*Kd*Kd2);
%шаг
h=0.01;
%начальные условия
X(1,1:4)=[0 0 0 0];
%матрица А (X'=AX+BY)
A=[0 1 0 0;
0 0 1 0;
0 0 0 1;
-a0 -a1 -a2 -a3];
%матрица B
B=[b3 b2 b1 b0]';
Y=[0 0 0 1]';
n=1;
k=1;
while(k<=10)
F(n,1:4)=(A*(X(n,1:4))'+B.*Y)';
X(n+1,1:4)=(X(n,1:4)'+h/10*(F(n,1:4))')';% Метод Эйлера
n=n+1;
k=k+1;
end
X(2,1:4)=X(n,1:4);
n=2;
I=[1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1];
while (n<=t/h)
F(n,1:4)=(A*(X(n,1:4))'+B.*Y)';
X(n+1,1:4)=(((I-5*h/12*A)^-1)*(X(n,1:4)'+h/12*(5*B.*Y+8*(F(n,1:4))'-(F(n-1,1:4))')))';
n=n+1;
end
i=1;
while(i<=n)
Xr(i)=X(i,1);
i=i+1;
end
%Найдем J0____________
i=0;
while(i<=t/h)
Xe(i+1)=1-exp((log(0.05)/2)*i*h);
i=i+1;
end
%нашли эталон
J=0;
i=1;
while(i<=t/h)
J=J+(Xr(i)-Xe(i))^2;
i=i+1;
end
%t=0:0.01:t;
%plot(t,Xr,t,Xe),grid on