Кривые второго порядка. Квадратичные формы

Высшая математика

Кривые второго порядка

Квадратичные формы

Содержание

1. Понятие квадратичной формы и способы ее записи

2. Знакоопределенность квадратичных форм

3. Критерии положительной и отрицательной определенностей

Литература

1. Понятие квадратичной формы и способы ее записи

Квадратичной формой  (х>1>, х>2>, …, x>n>) n действительных переменных х>1>, х>2>, …, x>n> называется сумма вида

,(1)

где a>ij> – некоторые числа, называемые коэффициентами. Не ограничивая общности, можно считать, что a>ij> = a>ji>.

Квадратичная форма называется действительной, если a>ij>  ГR. Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (1) соответствует единственная симметричная матрица

то есть АТ = А. Следовательно, квадратичная форма (1) может быть записана в матричном виде  (х) = хТАх, где

хТ = (х>1> х>2> … x>n>). (2)

И, наоборот, всякой симметричной матрице (2) соответствует единственная квадратичная форма с точностью до обозначения переменных.

Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма называется невырожденной, если невырожденной является ее матрица А. (напомним, что матрица А называется невырожденной, если ее определитель не равен нулю). В противном случае квадратичная форма является вырожденной.

Пример 1.

Записать матрицу квадратичной формы

 (х>1>, х>2>, x>3>) = – 6х>1>х>2> – 8х>1>х>3> + + 4х>2>х>3> –

и найти ее ранг.

Решение.

 r(A) = 3 

квадратичная форма невырождена.

2. Знакоопределенность квадратичных форм

Квадратичная форма (1) называется положительно определенной (или строго положительной), если (х) > 0, для любого х = (х>1>, х>2>, …, x>n>), кроме х = (0, 0, …, 0).

Матрица А положительно определенной квадратичной формы (х) также называется положительно определенной. Следовательно, положительно определенной квадратичной форме соответствует единственная положительно определенная матрица и наоборот.

Квадратичная форма (1) называется отрицательно определенной (или строго отрицательной), если (х) < 0, для любого х = (х>1>, х>2>, …, x>n>), кроме х = (0, 0, …, 0).

Аналогично как и выше, матрица отрицательно определенной квадратичной формы также называется отрицательно определенной.

Следовательно, положительно (отрицательно) определенная квадратичная форма (х) достигает минимального (максимального) значения (х*) = 0 при х* = (0, 0, …, 0).

Отметим, что большая часть квадратичных форм не является знакоопределенными, то есть они не являются ни положительными, ни отрицательными. Такие квадратичные формы обращаются в 0 не только в начале системы координат, но и в других точках.

Пример 2.

Определить знакоопределенность следующих квадратичных форм.

1)

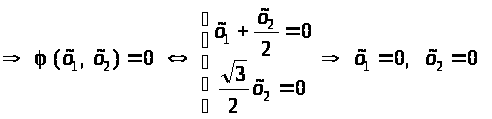
т. е. квадратичная форма является положительно определенной.

2)

т. е. квадратичная форма является отрицательно определенной.

3)

данная квадратичная форма не является знакоопределенной, так как она равна 0 во всех точках прямой х>1> = –х>2>, а не только в начале системы координат.

Когда n > 2 требуются специальные критерии для проверки знакоопределенности квадратичной формы. Рассмотрим их.

Главными минорами квадратичной формы называются миноры:

то есть это миноры порядка 1, 2, …, n матрицы А, расположенные в левом верхнем углу, последний из них совпадает с определителем матрицы А.

3. Критерий положительной и отрицательной определенности

Критерий положительной определенности (критерий Сильвестра)

Для того чтобы квадратичная форма  (х) = хТАх была положительно определенной, необходимо и достаточно, что все главные миноры матрицы А были положительны, то есть:

М>1> > 0, M>2> > 0, …, M>n> > 0.

Критерий отрицательной определенности

Для того чтобы квадратичная форма  (х) = хТАх была отрицательно определенной, необходимо и достаточно, чтобы ее главные миноры четного порядка были положительны, а нечетного – отрицательны, то есть:

М>1> < 0, M>2> > 0, М>3> < 0, …, (–1)n M>n> > 0.

Пример 3.

При каких значениях а и в квадратичная форма будет положительно определенной?

 (х>1>, х>2>, x>3>) =

Решение.

Построим матрицу А и найдем ее главные миноры.

М>1> = 1 > 0,

= а – 1 > 0  а > 1.

= ав – а – в > 0  в > .

Ответ:

а > 1, в > .

Пример 4.

При каких значениях а и в квадратичная форма будет отрицательно определенной?

 (х>1>, х>2>, x>3>) =

Решение.

М>1> = –1 < 0,

= –а – 1 > 0  а < –1.

= –ав – а – в < 0  в > – .

Ответ

а < –1, в > –.

Пример 5.

Доказать, что квадратичная форма

 (х>1>, х>2>, x>3>) =

положительно определена.

Решение.

Воспользуемся критерием Сильвестра. Построим матрицу А и найдем главные миноры матрицы А.

М>1> = 6 > 0, = 26 > 0, М>3> =  А  = 162 > 0

  (х>1>, х>2>, x>3>)

положительно определенная квадратичная форма.

Литература

1. Гусак А. А. Аналитическая геометрия и линейная алгебра.– Мн.: Тетрасистемс, 1998.

2. Овсеец М. И., Светлая Е. М. Сборник задач по высшей математике. Учебное издание.– Мн.: ЧИУиП, 2006.– 67 с.