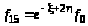Краевые задачи и разностные схемы
Реферат з курсу “Введение в численные методы”
Тема: “КРАЕВЫЕ ЗАДАЧИ И РАЗНОСТНЫЕ СХЕМЫ”
Содержание
1. Приведение к системе уравнений первого порядка
2. Разностное представление систем дифференциальных уравнений
3. Разностные системы уравнений для краевых задач
4. Краевые задачи второго порядка
5. Разностные схемы для уравнений в частных производных
6. Повышение точности разностных схем
7. Сеточные методы для нестационарных задач
Литература
1. Приведение к системе уравнений первого порядка
Для решения систем дифференциальных уравнений высокого порядка методами конечных разностей в первую очередь возникает потребность преобразования исходной системы в систему дифференциальных уравнений первого порядка с соответствующим образом преобразованными начальными или граничными условиями. И уже далее реализовывать численную процедуру решения.
Преобразование в систему уравнений первого порядка не единственно. Наиболее популярные из них в большинстве своем касаются линейных систем с постоянными или переменными коэффициентами. Основная идея всех методов состоит во введении новых переменных и выполнении замены высших производных этими переменными.
Пусть неоднородное дифференциальное уравнение высокого порядка задано в виде:

где  – соответственно i-тая
производная искомого решения и ее
значение в начальный момент,
– соответственно i-тая
производная искомого решения и ее
значение в начальный момент,
 – функция, описывающая внешнее
воздействие на динамический объект.
– функция, описывающая внешнее
воздействие на динамический объект.
Обозначим первую производную
искомой функции новой переменной
 ,
первую производную
,
первую производную
 – следующей переменной:
– следующей переменной:
 ,
первую производную
,
первую производную
 – переменной
– переменной
 и т.д.. Таким образом из исходной системы
мы сформируем
и т.д.. Таким образом из исходной системы
мы сформируем
 дифференциальное уравнение первого
порядка:
дифференциальное уравнение первого
порядка:

При таких заменах производных
искомой функции
 ее n-ная
производная оказывается равной первой
производной от
ее n-ная
производная оказывается равной первой
производной от
 :
:

В результате, эквивалентная система дифференциальных уравнений первого порядка примет следующий вид:
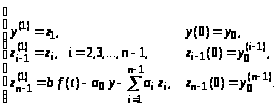
В случае, когда правая часть
представлена взвешенной суммой функции
 и ее производных и в целом дифференциальное
уравнение имеет вид
и ее производных и в целом дифференциальное
уравнение имеет вид

то его преобразование в систему
уравнений первого порядка с новыми
переменными
 осуществляется по следующим формулам:
осуществляется по следующим формулам:

Такое преобразование сохраняет
коэффициенты исходного уравнения
неизменными и исключает производные в
правой части от
 .
Начальные условия для новых переменных
здесь приходится пересчитывать по
достаточно сложным соотношениям.
.
Начальные условия для новых переменных
здесь приходится пересчитывать по
достаточно сложным соотношениям.
И, наконец, приведем еще один вариант разложения на систему уравнений первого порядка исходного неоднородного уравнения с производными в правой части:

Замена переменных в отличие от предыдущего случая производится без сохранения коэффициентов исходного уравнения:

Производные искомой функции
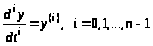 можно выразить через вновь введенные
переменные
можно выразить через вновь введенные
переменные
 путем многократного дифференцирования
левой и правой части соотношения для y
с подстановкой после
каждого дифференцирования производных
путем многократного дифференцирования
левой и правой части соотношения для y
с подстановкой после
каждого дифференцирования производных
 :
:

Умножив каждое выражение для
 на коэффициенты
на коэффициенты
 и просуммировав правые и левые члены
равенств, получим уравнение, которое
отличается от исходного лишь коэффициентами
при производных в правых частях. Чтобы
добиться тождественности, необходимо
коэффициенты при соответствующих
производных приравнять и разрешить
полученную систему уравнений относительно
неизвестных
и просуммировав правые и левые члены
равенств, получим уравнение, которое
отличается от исходного лишь коэффициентами
при производных в правых частях. Чтобы
добиться тождественности, необходимо
коэффициенты при соответствующих
производных приравнять и разрешить
полученную систему уравнений относительно
неизвестных
 .
.
Система уравнений имеет вид:

В векторно-матричной форме это уравнение и его решение записываются в следующем виде:

где  – вектор известных коэффициентов,
– вектор известных коэффициентов,
 – вектор искомых коэффициентов,
– вектор искомых коэффициентов,
 – соответственно прямая и
обратная верхне-треугольные матрицы
коэффициентов. Первая из них выглядит
так:
– соответственно прямая и
обратная верхне-треугольные матрицы
коэффициентов. Первая из них выглядит
так:
 .
.
Обратная матрица удобна при
использовании математических пакетов
для решения векторно-матричного
уравнения. Если
 ,
то коэффициенты
,
то коэффициенты
 легко вычисляются последовательной
подстановкой значений
легко вычисляются последовательной
подстановкой значений
 ,
начиная с
,
начиная с
 .
.
Начальные условия для
 вычисляются по выражениям для
вычисляются по выражениям для
 следующим образом:
следующим образом:

или в векторно-матричной форме:
 ,
,


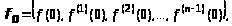
 .
.
2. Разностное представление систем дифференциальных уравнений
Представление системы дифференциальных уравнений первого порядка с начальными условиями

можно заменить системой
конечно-разностных уравнений первого
порядка с целочисленной независимой
переменной i ( ):
):
 ,
,
погрешность аппроксимации которого пропорциональна сеточному шагу h.
Выше было уже показано, как можно
уменьшить погрешность аппроксимации,
делая ее пропорциональной
 .
В частности это можно сделать, использовав
среднее арифметическое двух разностей
первого порядка: “вперед” и “ назад”.
.
В частности это можно сделать, использовав
среднее арифметическое двух разностей
первого порядка: “вперед” и “ назад”.

При такой замене производной мы
получаем систему разностных уравнений,
состоящую из разностных уравнений
второго порядка, требующих, кроме
известного вектора начальных условий
 ,
еще один дополнительный вектор
,
еще один дополнительный вектор
 :
:
 .
.
Дополнительный вектор начальных условий достаточно вычислить по формуле Эйлера. Он и определит дополнительное начальное условие с ошибкой, пропорциональной второй степени h:

Подстановка таких начальных
условий в решение сохранит погрешность
результатов на уровне
 .
В таком случае говорят, что разностная
схема имеет второй порядок точности.
.
В таком случае говорят, что разностная
схема имеет второй порядок точности.
3. Разностные системы уравнений для краевых задач
Исходные дифференциальные уравнения во многих физических и технических применениях решаются для случаев, когда заданы значения искомых функции и/или ее производных в различных точках интервала интегрирования и, в частности - на концах интервала. Такого рода уравнения в обыкновенных производных или системы из таких уравнений называются краевой задачей.
Общим методом решения краевой задачи является преобразование ее в систему алгебраических уравнений относительно множества неизвестных значений искомой функции, выбранных в точках, равномерно расположенных на оси абсцисс, т.е. заданных на сетке известных значений независимой переменной.
Для линейной системы уравнений
первого порядка, записанной в матричной
форме относительно вектора
 как
как
 ,
,
обязательно задается полный
набор краевых условий
 ,
включающий хотя бы одно значение
,
включающий хотя бы одно значение
 ,
или набор комбинаций из значений
,
или набор комбинаций из значений
 и
и

Обычно задаваемое граничное
значение совмещается с тем или иным
n-ным сеточным
значением независимой переменной. Это
позволяет обходиться без преобразования
граничных условий к ближайшей точке
сетки. Векторы
 ,
,
 ,
,
 и матрица
и матрица
 в общем случае приводятся к единичному
интервалу изменения независимой
переменной с помощью линейного
преобразования
в общем случае приводятся к единичному
интервалу изменения независимой
переменной с помощью линейного
преобразования
 ,
в котором
,
в котором
 с шагом по оси абсцисс равном
с шагом по оси абсцисс равном
 .
Благодаря этому производные в левых
частях единообразно заменяются
(M+1)-точечными
конечно-разностными выражениями через
искомые значения решения:
.
Благодаря этому производные в левых
частях единообразно заменяются
(M+1)-точечными
конечно-разностными выражениями через
искомые значения решения:
 .
.
Многоточечные представления производных получаются путем применения существующих соотношений между операторами дифференцирования, конечных разностей и сдвига:

Чтобы выразить значение производной
порядка k в
m-той точке
целочисленного интервала [0, n]
через ординаты функции
 необходимо выполнить следующие
операторные преобразования:
необходимо выполнить следующие
операторные преобразования:

Заменив конечно-разностные
операторы
 (после приравнивания нулю разностей со
степенями выше n)
выражениями с оператором сдвига
(после приравнивания нулю разностей со
степенями выше n)
выражениями с оператором сдвига
 и вспомнив, что
и вспомнив, что
 ,
получим в результате для k-той
производной в m-той
точке взвешенную сумму из ординат
искомой функции:
,
получим в результате для k-той
производной в m-той
точке взвешенную сумму из ординат
искомой функции:
 .
.
Погрешность аппроксимации
дифференциального оператора
конечно-разностным оператором для
центральной точки (m=n/2)
пропорциональна с наименьшим коэффициентом
величине
 и c наибольшим – для точек конца интервала.
и c наибольшим – для точек конца интервала.
Часто применяемые выражения конечно-разностной аппроксимации производных первого и второго порядков по трем-семи равномерно расположенным точкам приведены ниже в таблицах в виде коэффициентов, стоящих перед соответствующими ординатами функции. В левом верхнем углу таблиц записан общий множитель, а в крайней правой колонке – коэффициенты k1, k2 для формул погрешности.
Трех точечная аппроксимация первой производной
|
|
y(0) |
y(1) |
y(2) |
|
|
y’(0) |
-3 |
4 |
-1 |
2 |
|
y’(1) |
-1 |
0 |
1 |
-1 |
|
y’(2) |
1 |
-4 |
3 |
2 |
Четырех точечная аппроксимация первой производной
|
|
|
|
|
|
|
|
|
-11 |
18 |
-9 |
2 |
-3 |
|
|
-2 |
-3 |
6 |
-1 |
1 |
|
|
1 |
-6 |
3 |
2 |
-1 |
|
|
-2 |
9 |
-18 |
11 |
3 |
Пятиточечная аппроксимация первой производной
|
|
|
|
|
|
|
|
|
|
-25 |
48 |
-36 |
16 |
-3 |
12 |
|
|
-3 |
-10 |
18 |
-6 |
1 |
-3 |
|
|
1 |
-8 |
0 |
8 |
-1 |
2 |
|
|
-1 |
6 |
-18 |
10 |
3 |
-3 |
|
|
3 |
-16 |
36 |
-48 |
25 |
12 |
Шести точечная аппроксимация первой производной
|
|
|
|
|
|
|
|
|
|
|
-137 |
300 |
-300 |
200 |
-75 |
12 |
-10 |
|
|
-12 |
-65 |
120 |
-60 |
20 |
-3 |
2 |
|
|
3 |
-30 |
-20 |
60 |
-15 |
2 |
-1 |
|
|
-2 |
15 |
-60 |
20 |
30 |
-3 |
1 |
|
|
3 |
-20 |
60 |
-120 |
65 |
12 |
-2 |
|
|
-12 |
75 |
-200 |
300 |
-300 |
137 |
10 |
Семи точечная аппроксимация первой производной
|
|
|
|
|
|
|
|
|
|
|
|
-147 |
360 |
-450 |
400 |
-225 |
72 |
-10 |
60 |
|
|
-10 |
-77 |
150 |
-100 |
50 |
-15 |
2 |
-10 |
|
|
2 |
-24 |
-35 |
80 |
-30 |
8 |
-1 |
4 |
|
|
-1 |
9 |
-45 |
0 |
45 |
-9 |
1 |
-3 |
|
|
1 |
-8 |
30 |
-80 |
35 |
24 |
-2 |
4 |
|
|
-2 |
15 |
-50 |
100 |
-150 |
77 |
10 |
-10 |
|
|
10 |
-72 |
225 |
-400 |
450 |
-360 |
147 |
60 |
Трех точечная аппроксимация второй производной
|
|
|
|
|
|
|
|
1 |
-2 |
1 |
-12 , 2 |
|
|
1 |
-2 |
1 |
0 , -1 |
|
|
1 |
-2 |
1 |
12 , -2 |
Четырех точечная аппроксимация второй производной
|
|
|
|
|
|
|
|
|
2 |
-5 |
4 |
-1 |
55 , -6 |
|
|
1 |
-2 |
1 |
0 |
-5 , -2 |
|
|
0 |
1 |
-2 |
1 |
-5 , -2 |
|
|
-1 |
4 |
-5 |
2 |
55 , -6 |
Пятиточечная аппроксимация второй производной
|
|
|
|
|
|
|
|
|
|
35 |
-104 |
114 |
-56 |
11 |
-150 , 12 |
|
|
11 |
-20 |
6 |
4 |
-1 |
15 , -3 |
|
|
-1 |
16 |
-30 |
16 |
-1 |
0 , 2 |
|
|
-1 |
4 |
6 |
-20 |
11 |
15 , 3 |
|
|
11 |
-56 |
114 |
-104 |
35 |
150 , -12 |
Шести точечная аппроксимация второй производной
|
|
|
|
|
|
|
|
|
|
225 |
-770 |
1070 |
-780 |
305 |
-50 |
|
|
50 |
-75 |
-20 |
70 |
-30 |
5 |
|
|
-5 |
80 |
-150 |
80 |
-5 |
0 |
|
|
0 |
-5 |
80 |
-150 |
80 |
-5 |
|
|
5 |
-30 |
70 |
-20 |
-75 |
50 |
|
|
-50 |
305 |
-780 |
1070 |
-770 |
225 |
Семи точечная аппроксимация второй производной
|
|
|
|
|
|
|
|
|
|
|
812 |
-3132 |
5265 |
-5080 |
2970 |
-972 |
137 |
|
|
137 |
-147 |
-255 |
470 |
-285 |
93 |
-13 |
|
|
-13 |
228 |
-420 |
200 |
15 |
-12 |
2 |
|
|
2 |
-27 |
270 |
-490 |
270 |
-27 |
2 |
|
|
2 |
-12 |
15 |
200 |
-420 |
228 |
-13 |
|
|
-13 |
93 |
-285 |
470 |
-255 |
-147 |
137 |
|
|
137 |
-972 |
2970 |
-5080 |
5265 |
-3132 |
812 |
Например, производная первого
порядка
 в точках m=0,
3, 5 для семи точечной аппроксимации
будет иметь вид:
в точках m=0,
3, 5 для семи точечной аппроксимации
будет иметь вид:


 ,
,
 .
.
Аналогично выписываются выражения и для вторых производных в точках 0 и 2:

Таким образом, из приведенных таблиц можно выбрать аппроксимирующие выражения для производной в данной точке, включающие значения функции в точках нужного окружения.
4. Краевые задачи для уравнений второго порядка
При математическом описании реальных физических объектов чаще всего приходится иметь дело с дифференциальными уравнениями в обыкновенных или частных производных второго порядка с начальными, краевыми или граничными условиями.
Преобразование их в конечно-разностную систему алгебраических уравнений осуществляется аналогично: для каждой точки в области (интервале) интегрирования, где не задано краевое или граничное значение искомой функции, записывается исходное уравнение, в котором все производные выражены через заранее определенное число близлежащих ординат искомой функции, принадлежащих области, и вычислены все коэффициенты и функции независимых переменных в этой точке. К полученным таким образом уравнениям добавляются соотношения или значения функции и ее производных в точках границы области. В результате будет сформирована алгебраическая система уравнений с числом уравнений и неизвестных, равном общему числу точек области интегрирования.
В процессе формирования уравнений особое внимание необходимо обращать на замену производных конечно-разностными эквивалентами в приграничных точках. В выражениях последних должны отсутствовать неизвестные значения функции в точках, расположенных вне области интегрирования. Это достигается многократным применением оператора сдвига к соответствующему конечно-разностному оператору.
Если в центральных точках точность аппроксимации производных с n точками удовлетворяет поставленным требованиям и эту точность желательно сохранить и в приграничных точках заданных областей, то для последних выбирают аппроксимирующие формулы, построенные для (n+1)-й точки или более.
Рассмотрим примеры аппроксимации дифференциальных уравнений с краевыми условиями конечно-разностной системой алгебраических уравнений. Эти аппроксимации в литературе получили название "разностные схемы". Ниже в четырех таблицах приведены четыре варианта конечно-разностной аппроксимации одной и той же краевой задачи, для которой известно точное решение. Вид уравнения, условия на границе интервала, решение аналитическое и вычисленное в заданных точках с 12 значащими цифрами приведены в правой крайней колонке первой таблицы. В левых колонках первой и в трех остальных таблицах записаны системы алгебраических уравнений, полученных применением трех-, пяти-, пяти-шести- и семи точечной аппроксимации второй производной в заданном уравнении. Справа от уравнений приведены решения алгебраических уравнений тоже с 12-ю значащими цифрами.
|
Система уравнений с трехточечным представлением производных |
Вектор разностного решения с шагом h=0.1 |
|
|
-199 |
0.0186590989712 |
0.0186415437361 |
|
100 |
0.0361316064473 |
0.0360976603850 |
|
100 |
0.0512427953890 |
0.0511947672548 |
|
100 |
0.0628415300546 |
0.0627828520998 |
|
100 |
0.0698118753674 |
0.0697469636621 |
|
100 |
0.0710840847137 |
0.0710183518969 |
|
100 |
0.0656455142231 |
0.0655851465687 |
|
100 |
0.0525504484304 |
0.0525024675253 |
|
100 |
0.0309298757856 |
0.0309018656257 |
|
Система уравнений для пяти-точечного представления производных |
Вектор решения |
|
-9940 |
0.0186406186406 |
|
8000 |
0.0360968696594 |
|
-500 |
0.0511941848390 |
|
-500 |
0.0627825213460 |
|
-500 |
0.0697468774179 |
|
-500 |
0.0710184988305 |
|
-500 |
0.0655854996422 |
|
-500 |
0.0525029672554 |
|
-500 |
0.0309024932693 |
|
Система уравнений для пяти- и шести точечного представления производных |
Вектор решения |
|
-3720 |
0.0186415486274 |
|
8000 |
0.0360976918947 |
|
-500 |
0.0511948294923 |
|
-500 |
0.0627829167486 |
|
-500 |
0.0697469746974 |
|
-500 |
0.0710183243686 |
|
-500 |
0.0655851063829 |
|
-500 |
0.0525024168959 |
|
250 |
0.0309018105849 |
|
Система уравнений для семиточечного представления производных |
Вектор решения |
|
-7260 |
0.0186415513486 |
|
11400 |
0.0360976659970 |
|
-1350 |
0.0511947713313 |
|
10 |
0.0627828547351 |
|
10 |
0.0697469648318 |
|
10 |
0.0710183515790 |
|
100 |
0.0655851447467 |
|
100 |
0.0525024640963 |
|
-650 |
0.0309018602217 |
В этой задаче весь интервал интегрирования [0,1] был разбит на 10 равных частей с шагом h=0.1. Из одиннадцати точек в двух крайних искомая функция x(t) была задана, поэтому уравнения записывались для девяти внутренних точек, в которых значения функции требовалось найти.
5. Разностные схемы для уравнений в частных производных
Конечно-разностная аппроксимация дифференциальных уравнений в частных производных, называемая в литературе методом сеток, использует те же конечно-разностные выражения производных через значения искомой функции, которые приведены в таблицах выше. Однако есть особенности, которые связаны с наличием у каждой рассматриваемой точки соседних точек не только по направлениям осей независимых переменных, но и во множестве других наклонных направлений.
Поэтому, в случае использования многоточечных (более трех точек) формул для производных, выражения последних могут разрабатываться дополнительно для каждого применения.
Наиболее удобным в разработке многоточечных конечно-разностных выражений для уравнений в частных производных является операторный метод, основанный на учете взаимосвязи оператора дифференцирования с операторами сдвига по направлениям различных независимых переменных. Рассмотрим его применение на примере построения разностных формул для двумерных уравнений в частных производных второго порядка.
Характерным представителем уравнений в частных производных второго порядка является уравнение Лапласа:

 ,
,
где  – непрерывная функция, заданная на
границе области.
– непрерывная функция, заданная на
границе области.
Область численного решения уравнения разобьем на клетки системой вертикальных и горизонтальных прямых, проходящих через равномерно расположенные с шагом h точки на осях координат соответственно x и y:

Значения функции в узлах сетки
обозначим через
 и для каждой точки области решений
частные производные из уравнения заменим
соответствующим (например, трех точечным)
симметричным конечно-разностным
выражением для внутренних точек и для
точек вблизи границ таким несимметричным,
чтобы значения функций не выходили за
пределы области:
и для каждой точки области решений
частные производные из уравнения заменим
соответствующим (например, трех точечным)
симметричным конечно-разностным
выражением для внутренних точек и для
точек вблизи границ таким несимметричным,
чтобы значения функций не выходили за
пределы области:

После подстановки в уравнение Лапласа этих выражений для каждой внутренней точки области будет получена система алгебраических уравнений следующего вида:

В качестве примера, демонстрирующего
применение метода сеток, приведем
решение уравнения Лапласа для прямоугольной
области с количеством узлов
 и значениями функции на границе, как
показано ниже:
и значениями функции на границе, как
показано ниже:
|
u(0,0) |
0.5 |
0.476 |
0.404 |
0.294 |
0.154 |
0 |
|
0.5 |
u(1,1) |
u(1,2) |
u(1,3) |
u(1,4) |
u(1,5) |
0 |
|
0.476 |
u(2,1) |
u(2,2) |
u(2,3) |
u(2,4) |
u(2,5) |
0 |
|
0.404 |
u(3,1) |
u(3,2) |
u(3,3) |
u(3,4) |
u(3,5) |
0 |
|
0.294 |
u(4,1) |
u(4,2) |
u(4,3) |
u(4,4) |
u(4,5) |
0 |
|
0.154 |
u(5,1) |
u(5,2) |
u(5,3) |
u(5,4) |
u(5,5) |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Уравнения для 25 внутренних точек u(i,k):
|
0.5-4·u(1,1)+u(1,2)+u(2,1) +0.5=0, u(1,1)-4·u(2,1)+u(2,2)+u(3,1)+0.476=0, u(2,1)-4·u(3,1)+u(3,2)+u(4,1)+0.404=0, u(3,1)-4·u(4,1)+u(4,2)+u(5,1)+0.294=0, u(4,1)-4·u(5,1)+u(5,2)+0.154=0, 0.476+u(1,1)-4·u(1,2)+u(1,3)+u(2,2)=0, u(1,2)+u(2,1)-4·u(2,2)+u(2,3)+u(3,2)=0, u(2,2)+u(3,1)-4·u(3,2)+u(3,3)+u(4,2)=0, u(3,2)+u(4,1)-4·u(4,2)+u(4,3)+u(5,2)=0, u(4,2)+u(5,1)-4·u(5,2)+u(5,3)=0, 0.404+u(1,2)-4·u(1,3)+u(1,4)+u(2,3) =0, u(1,3)+u(2,2)-4·u(2,3)+u(2,4)+u(3,3)=0, u(2,3)+u(3,2)-4·u(3,3)+u(3,4)+u(4,3)=0 |
u(3,3)+u(4,2)-4·u(4,3)+u(4,4)+u(5,3)=0, u(4,3)+u(5,2)-4·u(5,3)+u(5,4)=0, 0.294+u(1,3)-4·u(1,4)+u(1,5)+u(2,4) =0, u(1,4)+u(2,3)-4·u(2,4)+u(2,5)+u(3,4)=0, u(2,4)+u(3,3)-4·u(3,4)+u(3,5)+u(4,4)=0, u(3,4)+u(4,3)-4·u(4,4)+u(4,5)+u(5,4)=0, u(4,4)+u(5,3)-4·u(5,4)+u(5,5)=0, 0.154+u(1,4)-4·u(1,5)+u(2,5) =0, u(1,5)+u(2,4)-4·u(2,5)+u(3,5)=0, u(2,5)+u(3,4)-4·u(3,5)+u(4,5)=0, u(3,5)+u(4,4)-4·u(4,5)+u(5,5)=0, u(4,5)+u(5,4)-4·u(5,5)=0. |
Результат решения системы из 25 уравнений представлен в таблице:
|
u(0,0) |
0.5 |
0.476 |
0.404 |
0.294 |
0.154 |
0 |
|
0.5 |
0.444618 |
0.389236 |
0.316975 |
0.225193 |
0.116966 |
0 |
|
0.476 |
0.389236 |
0.319355 |
0.249474 |
0.172833 |
0.0886772 |
0 |
|
0.404 |
0.316975 |
0.249474 |
0.188730 |
0.127986 |
0.0649079 |
0 |
|
0.294 |
0.225193 |
0.172833 |
0.127986 |
0.0854773 |
0.0429672 |
0 |
|
0.154 |
0.116966 |
0.0886772 |
0.0649079 |
0.0429672 |
0.0214836 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Следует отметить, что в трех
точечном представлении конечно-разностные
выражения производных второго порядка
для внутренних и приграничных точек
совпадают. Это позволяет для прямоугольных
областей, заменив двумерную индексацию
неизвестных
 одномерной
одномерной
 ,
,
преобразовать систему уравнений в векторно-матричную форму записи с блочно-диагональной матрицей коэффициентов, которая удобна для решения алгебраических уравнений с числом неизвестных более 100 на векторных вычислительных машинах:
 ,
,
 ,
,
 , I
, I
– матрицы, соответственно, блочная, коэффициентов и единичная;
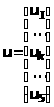 ,
,  ,
,  ,
,
 ,
,  ,
, 
– соответственно, векторы неизвестных и правых частей уравнения со своими блочными компонентами.
В конечно-разностном представлении уравнения Лапласа каждое уравнение является для соответствующей точки области формулой вычисления среднего арифметического совокупности значений функции в соседних точках:
 .
.
Погрешность конечно-разностного представления уравнения Лапласа в виде системы алгебраических уравнений определяется погрешностью аппроксимации производных, которая для трех точечного варианта, приведенного выше, пропорциональна шагу сетки.
Естественно желание повысить точность аппроксимации лапласиана, добавив в структуру его конечно-разностного представления значения функции в дополнительных точках при сохранении суммирования значений из окружающих точек.
6. Повышение точности разностных схем
Оператор сдвига, преобразующий
значение функции в точке z
в значение функции в точке z+h
выражается через оператор
производной
 ,
как
,
как
 ,
а его применение представляется
выражением:
,
а его применение представляется
выражением:

Обозначив операторные выражения для сдвига значений функции по осям x, y соответственно

несложно записать с их помощью следующие операторные выражения:

Во фрагменте сетки, изображенной
в виде таблицы
 ,
для каждой представленной индексом
точки записано значение функции,
выраженное через значение функции в
центральной точке, преобразованное
соответствующими операторами сдвига:
,
для каждой представленной индексом
точки записано значение функции,
выраженное через значение функции в
центральной точке, преобразованное
соответствующими операторами сдвига:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим суммы значений функций, симметрично располагающихся вокруг центральной точки:


Подобными преобразованиями операторных выражений можно получить формулы для следующих сумм:
 и любых других.
и любых других.
Включая выражения для частичных сумм в единую сумму с различными весовыми коэффициентами, пренебрегая выражениями с производными и лапласианами высоких порядков, получают конечно-разностные формулы, аппроксимирующие уравнение Лапласа в заданной точке и содержащие большее число значений искомой функции.
Например, из выражения для
 непосредственно следует
непосредственно следует

что, после пренебрежения слагаемыми
в правой части, полностью соответствует
трех точечной разностной аппроксимации
частных производных. Суммируя
 и
и
 с весами соответственно 4 и 1, получим
аппроксимацию производных по значениям
в восьми точках:
с весами соответственно 4 и 1, получим
аппроксимацию производных по значениям
в восьми точках:

Если значения частных производных в точках области решения малы, то радикальным способом увеличения точности аппроксимации уравнения является уменьшение шага сетки.
При задании в правой части
уравнения Лапласа функции g(x,y)
последняя в приведенных конечно-разностных
суммах должна заменить
 на
на
 ,
,
 – на
– на
 и т.д.:
и т.д.:

7. Сеточные методы для нестационарных задач
Уменьшение величины шага приводит к квадратичному возрастанию числа точек в области решения, а следовательно, к порядку алгебраической системы уравнений. Одним из путей уменьшения числа уравнений является метод прямых, который позволяет аппроксимировать дифференциальное уравнение в частных производных системой дифференциальных уравнений в обыкновенных производных с краевыми условиями. Для этого частные производные по одной из независимых переменных не заменяют конечно-разностным эквивалентом. Если в уравнении оставлена пространственная переменная, то получаемая система будет краевой задачей со всеми сложностями ее решения, рассмотренными ранее.
Существенным будет выигрыш лишь при решении дифференциальных уравнений в частных производных, описывающих нестационарные процессы. К ним относятся уравнения, подобные уравнениям теплопроводности и волновому. Этим уравнениям кроме условий на границе задают еще и начальное распределение искомой функции во всех точках области решения.
Применение метода прямых рассмотрим на примере решения уравнения теплопроводности следующего вида:
 ,
,
которое описывает распространение тепла (изменение температуры) вдоль металлического стержня, вваренного своими концами в две металлические пластины с разными, постоянно поддерживаемыми на них температурами. Коэффициент B, характеризующий свойства материала, возьмем равным 1.
Пусть расстояние между пластинами
равно единице, т.е.
 ,
значения температуры на пластинах
,
значения температуры на пластинах
 и начальное распределение температуры
по длине
и начальное распределение температуры
по длине
 .
.
Разобьем единичную длину стержня
на 8 равных частей (h=1/8)
и обозначим значение
температуры в каждой точке через
 ,
k=0,1,..., Применим
пяти- и шести точечную аппроксимацию
частной производной второго порядка:
первую симметричную - для внутренних
точек, и вторую (несимметричную) – для
приграничных точек
,
k=0,1,..., Применим
пяти- и шести точечную аппроксимацию
частной производной второго порядка:
первую симметричную - для внутренних
точек, и вторую (несимметричную) – для
приграничных точек
 .
Температуры в точках с k=0
и k=8
заданы: 100° и 0°.
.
Температуры в точках с k=0
и k=8
заданы: 100° и 0°.

После замены производных
конечно-разностными эквивалентами
получим следующую систему линейных
дифференциальных уравнений с начальными
условиями
 в векторно-матричной форме:
в векторно-матричной форме:

Чтобы получить представление о влиянии порядка разностных формул на вид записи и точность решения задачи, в таблице приведены системы уравнений для 5- и 3-точечных выражений частных производных:
|
Произ-водная |
|
|
|
|
T1’= |
-15T1-4T2+14T3-6T4+T5+1000 |
-20T1+6T2+4T3-T4+1100 |
-2T1+T2+100 |
|
T2’= |
16T1-30T2+16T3-T4-100 |
16T1-30T2+16T3-T4-100 |
T1-2T2+T3 |
|
T3’= |
-T1+16T2-30T3+16T4-T5 |
-T1+16T2-30T3+16T4-T5 |
T2-2T3+T4 |
|
T4’= |
-T2+16T3-30T4+16T5-T6 |
-T2+16T3-30T4+16T5-T6 |
T3-2T4+T5 |
|
T5’= |
-T3+16T4-30T5+16T6-T7 |
-T3+16T4-30T5+16T6-T7 |
T4-2T5+T6 |
|
T6’= |
-T4+16T5-30T6+16T7 |
-T4+16T5-30T6+16T7 |
T5-2T6+T7 |
|
T7’= |
T3-6T4+14T5-4T6-15T7 |
-T4+4T5+6T6-20T7 |
T6-2T7 |
Полученные системы обыкновенных
дифференциальных уравнений можно решать
любым из рассмотренных ранее численным
методом. Правда, появляется особенность
в выборе шага интегрирования по времени,
который теперь зависит еще и от шага
разбиения области решения по
пространственной переменной. В случае
аппроксимации производной по времени
конечными разностями “вперед”
соотношение между шагом по временной
переменной
 и по пространственной
и по пространственной
 должно подчиняться
следующему неравенству:
должно подчиняться
следующему неравенству:
 .
При несоблюдении неравенства решение
будет численно неустойчивым и
интегрирование по времени с каждым
шагом будет давать неограниченно
возрастающие значения.
.
При несоблюдении неравенства решение
будет численно неустойчивым и
интегрирование по времени с каждым
шагом будет давать неограниченно
возрастающие значения.
В рассматриваемом примере
 =
= 0,015625,
поэтому интегрирование трех систем по
формулам Рунге-Кутта было выполнено с
шагом по времени
0,015625,
поэтому интегрирование трех систем по
формулам Рунге-Кутта было выполнено с
шагом по времени
 =
0,001 до значения 0,01 и с шагом 0,005 – до
значения времени, равного 0,75. Выборка
ряда значений температуры из решений
в интервале времени (0,0.75] показана в
таблице колонками из трех чисел,
соответствующих сверху-вниз трем
приведенным выше системам.
=
0,001 до значения 0,01 и с шагом 0,005 – до
значения времени, равного 0,75. Выборка
ряда значений температуры из решений
в интервале времени (0,0.75] показана в
таблице колонками из трех чисел,
соответствующих сверху-вниз трем
приведенным выше системам.
|
|
|
|
|
|
|
|
|
|
0.01 |
36.32 36.82 23.97 |
152 466 3.434 |
0.9573 1.038 0.3456 |
-0.005579 0.004583 0.02668 |
-0.02021 -0.02009 0.001666 |
-0.001651 -0.002840 73610^(-5) |
0.009336 -0.0001931 3.93410^(-6) |
|
0.02 |
52.52 52.39 37.89 |
20.86 21.00 9.682 |
6.165 6.287 1.825 |
1.298 1.347 0.2702 |
0.1715 0.1810 0.0328 |
0.01656 0.002515 0.003367 |
0.03366 -0.01559 0.0002973 |
|
0.05 |
69.3 69.17 57.27 |
42.88 42.79 26.61 |
23.52 23.50 10.15 |
11.37 11.37 3.243 |
4.821 4.826 0.884 |
1.773 1.767 0.2089 |
0.5202 0.5142 0.04223 |
|
0.1 |
77.99 77.98 69.09 |
57.61 57.58 42.81 |
40.14 40.12 23.71 |
26.27 26.25 11.75 |
16 15.99 5.222 |
826 829 2.076 |
3.842 3.854 0.6867 |
|
0.25 |
85.43 85.43 80.18 |
71.18 71.18 61.57 |
57.51 57.51 45.12 |
44.6 44.60 31.4 |
32.51 32.51 20.52 |
21.18 21.18 12.13 |
10.43 10.43 5.581 |
|
0.5 |
87.32 87.32 85.39 |
74.67 74.67 71.1 |
62.07 62.07 57.41 |
49.54 49.54 44.5 |
37.07 37.07 32.42 |
24.67 24.67 21.11 |
12.32 12.32 10.39 |
|
0.75 |
87.48 87.48 86.87 |
74.97 74.97 73.84 |
62.46 62.46 60.99 |
49.96 49.96 437 |
37.46 37.46 35.99 |
24.97 24.97 23.84 |
12.48 12.48 11.87 |
Как видно, трех точечная аппроксимация по сравнению с пятиточечной дает худший результат. Точное решение в установившемся режиме дает изменение температуры на каждой одной восьмой длины стержня 12,5°С. Пятиточечная аппроксимация в данной задаче дала погрешность в сотые доли процента.
Литература
Калашников В. И. Введение в численные методы: Учеб. пособие. – Харьков: НТУ “ХПИ”, 2002. – 132 с.
Рено Н.Н. АЛГОРИТМЫ ЧИСЛЕННЫХ МЕТОДОВ: МЕТОДИЧЕСКОЕ ПОСОБИЕ ДЛЯ ВУЗОВ. Изд-во: "Книжный дом Университет" (КДУ), 2007. – 24с.
Самарcкий А. А. Задачи и упражнения по численным методам. Изд.3 Изд-во: КомКнига, ЛКИ, 2006. – 208с.
Самарский А.А. Введение в численные методы Учебное пособие для вузов 3-е изд.,стер. ЛАНЬ, 2005. – 288с.
Турчак Л. И., Плотников П. В. Основы численных методов. Изд-во: ФИЗМАТЛИТ®, 2003. – 304с.
Тыртышников Е.Е. МЕТОДЫ ЧИСЛЕННОГО АНАЛИЗА (1-Е ИЗД.) УЧЕБ. ПОСОБИЕ Издательство "Академия/Academia", 2007. – 320с.
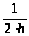













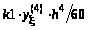




























 +100
+100 +0.1=0
+0.1=0 +0.2=0
+0.2=0 +0.3=0
+0.3=0 +0.4=0
+0.4=0 +0.5=0
+0.5=0 +0.6=0
+0.6=0 +0.7=0
+0.7=0 +0.8=0
+0.8=0 8+36=0
8+36=0