Контрольные задания для заочников по математике

Министерство образования Российской Федерации

государственный технический университет

МАТЕМАТИКА

Методические указания и контрольные задания

для студентов-заочников всех специальностей

Одобрено

редакционно-издательским советом

государственного

технического университета

2004

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ

Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса “Математика”, используя учебную литературу. Список рекомендуемой литературы приведен в методических указаниях. Студент может использовать также учебники и учебные пособия, не включенные в данный список, если эти пособия содержат соответствующие разделы учебного курса.

Контрольная работа выполняется в отдельной тетради. На обложке тетради необходимо указать название учебной дисциплины, номер контрольной работы, а также полностью фамилию, имя и отчество студента, его адрес, специальность, номер студенческой группы, шифр (номер зачетной книжки) и дату отправки работы в институт.

Задачи контрольной работы выбираются в соответствии с указаниями преподавателя из таблиц вариантов. Вариант определяется двумя последними цифрами номера зачетной книжки. Предпоследняя цифра номера определяет таблицу вариантов, последняя цифра номера определяет столбец в выбранной таблице. Представленная для рецензирования контрольная работа должна содержать все задачи, указанные преподавателем. Решения задач следует приводить в той последовательности, которая определена в таблице вариантов. Условие каждой задачи должно быть приведено полностью перед ее решением. Контрольная работа должна быть подписана студентом.

Зачет по контрольной работе выставляется по результатам рецензирования и собеседования. Перед собеседованием студент обязан исправить в работе ошибки, отмеченные рецензентом.

Зачет по контрольным работам является обязательным для допуска к сдаче зачетов и экзаменов, которые предусмотрены учебным планом.

ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

1. -10. Векторы a, b, c, d заданы координатами в некотором базисе. Показать, что векторы a, b, c образуют базис в пространстве, и найти координаты вектора d в этом базисе.

1. a=(3; 2; 2),b=(2; 3; 1),c=(1; 1; 3),d=(5; 1; 11).

2. a=(1; 2; 3),b=(-2; 3; - 2),c=(3; - 4; - 5),d=(6; 20; 6).

3. a=(4; 2; 5),b=(-3; 5; 6),c=(2; - 3; - 2),d=(9; 4; 18).

4. a=(1; 2; 4),b=(1; - 1; 1),c=(2; 2; 4),d=(-1; - 4; - 2).

5. a=(2; 3; 3),b=(-1; 4; - 2),c=(-1; - 2; 4),d=(4; 11; 11).

6. a=(1; 8; 4),b=(1; 3; 1),c=(-1; - 6; - 3),d=(1; 2; 3).

7. a=(7; 4; 2),b=(-5; 0; 3),c=(0; 11; 4),d=(31; - 43; - 20).

8. a=(3; 2; 1),b=(4; - 1; 5),c=(2; - 3; 1),d=(8; - 4; 0).

9. a=(1; 3; 3),b=(-4; 1; - 5),c=(-2; 1; - 6),d=(-3; 5; - 9).

10. a=(1; 5; 3),b=(2; 1; - 1),c=(4; 2; 1),d=(31; 20; 9).

11. -20. Даны координаты точек A1, A2, A3, A4. Известно, что отрезки A1A2, A1A3, A1A4 являются смежными ребрами параллелепипеда. Требуется найти:

длину ребра A1A2; 2) угол между ребрами A1A2 и A1A3; 3) площадь грани, содержащей вершины A1,A2,A3; 4) объем параллелепипеда; 5) уравнение прямой, проходящей через вершину A1 вдоль диагонали параллелепипеда; 6) уравнение плоскости A1A2A3; 7) угол между ребром A1A4 и гранью, содержащей вершины A1,A2,A3; 8) расстояние от вершины A4 до плоскости A1,A2,A3. Сделать чертеж.

11. A1(0; 3; 2),A2(-1; 3; 6),A3(-2; 4; 2),A4(0; 5; 4).

12. A1(4; 2; 5),A2(0; 7; 2),A3(0; 2; 7),A4(1; 5; 0).

13. A1(-1; 2; 0),A2(-2; 2; 4),A3(-3; 3; 0),A4(-1; 4; 2).

14. A1(4; 4; 10),A2(4; 10; 2),A3(2; 8; 4),A4(9; 6; 4).

15. A1(2; 2; 3),A2(1; 2; 7),A3(0; 3; 3),A4(2; 4; 5).

16. A1(4; 6; 5),A2(6; 9; 4),A3(2; 10; 10), A4(7; 5; 9).

17. A1(0; - 1; 2),A2(-1; - 1; 6),A3(-2; 0; 2),A4(0; 1; 4).

18. A1(3; 5; 4),A2(8; 7; 4),A3(5; 10; 4),A4(4; 7; 8).

19. A1(3; 0; 2),A2(2; 0; 6),A3(1; 1; 2),A4(3; 2; 4).

20. A1(10; 6; 6),A2(-2; 8; 2),A3(6; 8; 9),A4(7; 10; 3).

21. Даны уравнения двух сторон параллелограмма: x+2y+1=0 и 2x+y-3=0. Центр параллелограмма находится в точке A(1; 2). Найти уравнения двух других сторон. Сделать чертеж.

22. Даны две вершины треугольника A(2; 1), B(4; 9) и точка пересечения высот N(3; 4). Найти уравнения сторон треугольника. Сделать чертеж.

23. Даны две противоположные вершины квадрата A(1; 3) и C(-1; 1). Найти координаты двух его других вершин и составить уравнения сторон. Сделать чертеж.

24. Найти уравнения сторон треугольника, если заданы его вершина A(1; 3) и уравнения двух медиан x-2y+1=0, y-1=0. Сделать чертеж.

25. Известны уравнение одной из сторон квадрата x+3y-3=0 и точка пересечения диагоналей N(-2; 0). Найти уравнения остальных ее сторон. Сделать чертеж.

26. Уравнения боковых сторон равнобедренного треугольника 2x-y+8=0, x-2y-12=0. Точка N(4; 0) лежит на основании треугольника. Найти уравнение основания. Сделать чертеж.

27. Найти уравнения сторон треугольника, зная одну его вершину B(2; - 7), а также уравнения высоты 3x+y+11=0 и медианы x+2y+7=0, проведенных из различных вершин. Сделать чертеж.

28. Точка A(5; - 4) является вершиной квадрата, диагональ которого лежит на прямой x-7y-8=0. Написать уравнения сторон и второй диагонали этого квадрата. Сделать чертеж.

29. Уравнение основания равнобедренного треугольника x+y-1=0, уравнение боковой стороны x-2y-2=0. Точка N(-2; 0) лежит на другой боковой стороне. Найти уравнение этой стороны. Сделать чертеж.

30. Даны уравнения медиан треугольника 5x+4y=0 и 3x-y=0 и одна из его вершин A(-5; 2). Найти уравнения сторон треугольника. Сделать чертеж.

31. Составить уравнение и построить окружность, проходящую через точки A(1; 2), B(0; - 1) и C(-3; 0).

32. Составить уравнение и построить линию, расстояние каждой точки которой от точки A(0; 1) в два раза меньше расстояния ее до прямой y-4=0.

33. Составить уравнение и построить линию, сумма квадратов расстояний от каждой точки которой до точек A(-3; 0) и B(3; 0) равна 50.

34. Составить уравнение и построить линию, расстояние от каждой точки которой до точки A(-1; 1) вдвое меньше расстояния до точки B(-4; 4).

35. Составить уравнение и построить линию, сумма расстояний от каждой точки которой до точек A(-2; 0) и B(2; 0) равна 2.

36. Составить уравнение и построить линию, каждая точка которой находится на одинаковом расстоянии от точки F(2; 2) и оси Ox.

37. Составить уравнение и построить линию, расстояния каждой точки которой от точки A(2; 0) и от прямой 5x+8=0 относятся как 5: 4.

38. Составить уравнение и построить линию, расстояния каждой точки которой от начала координат и от точки A(5; 0) относятся как 2: 1.

39. Составить уравнение и построить гиперболу, проходящую через точку N(9; 8), если асимптоты гиперболы имеют уравнения y=±(2/3) x.

40. Составить уравнение и построить гиперболу, вершины и фокусы которой находятся в соответствующих фокусах и вершинах эллипса 5x2+8y2=40.

41. -50. Кривая задана уравнением в прямоугольной системе координат. Требуется: 1) найти уравнение кривой в полярной системе координат, полюс которой совмещен с началом прямоугольной системы координат, а полярная ось – с положительной полуосью Ox; 2) построить кривую по точкам со значениями полярного угла φk=kπ/16.

41. (x2+y2) 2 = 2(x2-y2); 42. (x2+y2) 2 = 4xy;

43. (x2+y2) 2/4 = x2-y2; `44. (x2+y2) 2 = 8xy;

45. (x2+y2) 2 = 6(x2-y2); 46. (x2+y2) 2 = 2(y2-x2);

47. (x2+y2) 2 = - 4xy; 48. (x2+y2) 2 = 4(y2-x2);

49. (x2+y2) 2 = - 8xy; 50. (x2+y2) 2 = 12xy.

ЭЛЕМЕНТЫ АЛГЕБРЫ

51. -60. Решить систему линейных уравнений методом Гаусса.

51.52.

3x1+ x2+ x3+ x4+ x5= 5,  x1+2x2+ x3+6x4+ x5=4,

2x1 - x2+3x3 = 4, 3x1 - x2 - x3+ x4+ =1,

 5x2+6x3+ x4+ =11.  x1+3x2+5x3 =9.

53.54.

3x1 - x2+ x3+6x4+ x5=6, 5x1+ x2+ x3+3x4+ x5=5,

 x1+ 5x3+ x4-7x5 =6,  - 2x2+4x3+ x4+ x5=3,

 x1+2x2+3x3+ x4+ x5 =6.  x1-3x2+5x3 =2.

55.56.

 - x1+ x2+ x3+2x4+ x5=4, -2x1 - x2+2x3 =2,

2x1 + x3 - 3x4+5x5=3,  x1+ x2+4x3+ x4+3x5=8,

3x1 - x3+6x4+ x5=6. 3x1+ x2 - x3 =5.

57.58.

2x1+ x3 - x4+ x5=2,  6x1+ x2+ x3+ 2x4+ x5=9,

4x1+ x2+ 3x3+ x4+2x5=7,  - x1 - x3+ 7x4+8x5=14,

 - x1+ x3+2x4+ x5=2.  x1+ 2x3+ x4+ x5=3.

59.60.

-2x1+ 3x3+ x4+ x5=5, 2x1+ 3x3+ x4 =4,

 3x1+ x2+ x3+6x4+2x5=9,  x1 - x3+2x4+3x5=4,

 - x1+ 2x3 - x4+2x5=3. 3x1+3x2+6x3+3x4+6x5=15.

61. -70. Для данной матрицы A построить обратную матрицу A-1. Правильность построения обратной матрицы проверить, используя матричное умножение.

61. 3 2 1 62.  1 - 5 3 63. 4 - 3 2

A= 2 3 1  A=  2 4 1  A= 2 5 - 3 

2 1 1. -3 3 - 7. 5 6 - 2.

64. -2 5 - 6 65. 2 - 1 - 1 66. 3 - 9 8

A=  1 7 - 5  A= 3 4 - 2  A= 2 - 5 5 

 4 2 - 1. 3 - 2 4. 2 - 1 1.

67. 1 1 - 1 68. 2 3 1 69. 7 - 5 0

A= 8 3 - 6  A= 4 - 1 5  A= 4 0 11

4 1 - 3. 1 - 2 4. 2 3 4.

70. 1 7 - 2

A= 3 5 1 

-2 5 - 5.

71. -80. Определить собственные значения и собственные векторы квадратной матрицы второго порядка.

71. -1 3  72. 4 - 1 73. -6 5 74. -4 - 3 

2 0 . -2 3.  2 - 3. -2 1 

75. -3 2  76. 1 - 2 77.  4 - 1 78. -1 3

 5 - 6. -3 - 4. -2 5. 2 - 2.

79.  1 - 2  80. 1 2

-3 6 . 3 2.

81. -90. Дано комплексное число z. Требуется:

1) записать число z в алгебраической, тригонометрической и показательной формах;

найти все корни уравнения w3+z=0, изобразить эти корни на плоскости комплексной переменной.

_ _ _

81. z=8/(1+i3).82. z=-8/(1+i).83. z=8/(1-i).

_ _ _

84. z=2/(1-i3).85. z=-2/(-i+3).86. z=1/(3+i).

_ _ _

87. z= - 4/(1-i3).88. z=-8/(-i+1).89. z=8/(1+i).

_

90. z=1/(3-i).

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

91. -100. Построить график функции y = f(x) посредством преобразования графика некоторой простейшей элементарной функции.

91. f(x) = (3x+2) / (2x+3).

92. f(x) = 3cos(2x – 5).

________________

93. f(x) =(4x2+7x –2) / (4x-1).

94. f(x) = 9x2 – 6x + 3.

95. f(x) = ln(x2 – 6x + 9).

96. f(x) = - 2sin(3x + 4).

97. f(x) =2x3 – 18x2 + 54x – 53.

98. f(x) =ln((x+1) - 2 / e2).

99. f(x) =

f(x) = (3x2 – 5x + 2) /(2x2 + x – 3).

101. -110. Haйти пределы функций, не пользуясь средствами дифференциального исчисления.

_________ _

101. а) lim (4x2 – x + 3 - 2x); б) lim (x – 1) – 1sin(1 – x);

x   x 1

в) lim (1 + x + x2) 1/x; г) lim (5x - 3x) /(7x – 4x).

x  0 x  0

102. а) lim (x2+2x–3) /(3x2+14x+15); б) lim x sin((2x + 1) / (x2+4x3));

x - 3 x  

в) lim (1 – 2sin2x) 1/xsinx; г) lim x – 2 ln(cos2x).

x  0 x  0

______ _______ _____

103. а) lim (38x4 + 1 + x + 3) / (3x + 2(1 + x2 + 9));

x  

б) lim sin2(x – 1) / (4x2 + 3x +2); в) lim ;

x   x

г) lim (e2x – 3ex + 2) /x.

x  0

__________ ______

104. а) lim (x2 + x + 1 - x2 - x); б) lim (1 – cos2x) /(x sinx);

x   x  0

в) lim((2x2+3x+4) /(2x2+x+1)) –x/2; г) lim [ln(1 + 3lnx) / ln(1 + 4lnx)].

x   x 1

105. а) lim (3x5 + 2x2 + 1) /(1 + 4x3 – x5); б) lim x – 2sin2(x2 + 2x);

x  x  0

в) lim ; г) lim (esinx – ex) /x.

x  0 x  0

_______________

106. а) lim (x2 + 4x - x2 + 6x + 1); б) lim (cos 5x) /(sin 2x);

x   x  /2

в) lim ((x2 + 7x + 8) /(x2 + 14x + 1)) – x/3; г) lim (e – ecosx ) /x.

x   x  0

_____

107. а) lim (x2 - 5x + 6) /(x3 - 8x + 8); б) lim (1 - 1 – x) – 1 sinx;

x  2 x  0

_____

в) lim (x + 1 + x) 3/x; г) lim x – 1 ln(cosx + sinx).

x  0 x  0

108. а) lim (3x4 – 2x2 + 1) /(2x4 + 3x2 – 2);

x  

б) lim (sinx – sin3x) /(sin6x – sin7x);

x  0

в) lim ; г) lim (ln cosx) /(cos3x – cosx).

x  0x  0

109. а) lim ; б) lim (cos8x – cos2x) /(cos6x – cos4x);

x5/2x  0

______

в) lim (9 –2x) 1/(4 – x); г) lim ln(x + x2 + 1) /x.

x  4x  0

____________

110. а) lim (x - x + 2) /(4x + 1 - 3); б) lim (sin2x– sinx) /(cos4x – cos2x);

x  2 x  0

в) lim ((2x + 1) /(3x +1)) 1/x; г) lim (ln(3 – 2tgx)) /cos2x.

x0 x  /4

111. -120. Исследовать на непрерывность функцию y = f(x), найти точки разрыва и определить их род. Построить схематический график функции.

111. 112. 113.

114. 115.

 (2x2 + 3) /5приx( - , 1] ;

116.  6 – 5xприx  (1, 3);

 x – 3приx  [3, +).

117. arctg.118. x ctgx.

119. .120.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ И ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ

121. -130. Найти производную функции одной переменной, исходя из определения производной.

y = tg2x.122. y = ln(3x + 1).123. y = cos(x2).

y = sin(x2 + 2x).125. y = ctg(3x - 2).126. y =  2x2 + 1.

127. y =  2 – cos3x.128. y =  2 + sin2x.129. y = e2x.

y = (x + 1) /(x – 1).

131. -140. Найти производные первого порядка данных функций, используя правила вычисления производных.

1) y = 4x4 + tgx; 2) y = x1/2 / sinx;

3) y = ctg5x / x3; 4) y = arctg(ex) + tg(arccos(ex)).

1) y = ln(tg(3x + 2)); 2) y =  1 – x2 arcsinx;

3) y = xtgx; 4) y = (x2 – 1) /(x2 + 1).

1) y = arccos(x2) + arcctg(x2); 2) xy = cos(x – y);

3) y = log2(2x + 1); 4) y = 1 – x2 / 1 + x2.

1) y = (2 - 5x) / 2 – 5x + x2; 2) y = ex – y;

3) y = 2 lnx – x; 4) y = sin2 3t, x = cos4 3t.

1) y = (arcsinx) 1 – x; 2) y = cos2 x + tg2x;

3) x3 + y3 – 3xy = 3; 4) x = t – sin2t, y = 1 – cos 2t.

1) y = sin2x/(1 + sin2x); 2) y = 3arctgx + (arctgx) 3,

3) y = (1 + x2) 1 + 2x; 4) y = tg3t, x = cos2 3t.

1) y = 3 –3x + (3x) –3; 2) y = (x – 1) log5(x2 – 1),

3) y = (x2 + 1) x; 4) y = tg(x2/y2).

1) y = ln(lg(log2x)); 2) y = (x2 + x + 1) /(x2 + 1);

3) y = (x + 1) x; 4) ex + y = x – y.

1) y = (x2 + 1) 3 – (x2 – 1) 3; 2) y = (ln5x) /(x4 – 1);

3) y = (tgx) ctgx; 4) x = t ctg(t2), y = t cos2(t2).

1) y = ln(x + x2 + 1); 2) y = x –sin2x;

3) y = 2/(x –1) + 1/(x2 – 1); 4) sin(x + y) + cos(x2 + y2) = 1.

141. -160. Построить график функции, используя общую схему исследования функции.

141. y = (x2 + 2x + 2) /(2 + x2) .142. y = (4 + x2) /(9 – x2).

143. y = (2 + 3x2) /(1 + x2).144. y = (x3 + 2x2 + 2) /(x2 + 1).

145. y = (x2 + 3x + 5) /(x – 1).146. y = (3x3 – 2) /x.

147. y = (2x2 +3x + 1) /(x – 2).148. y = x3/(x3 + 1).

149. y = (3 – 9x2) /(1 – 9x2).150. y = (x3 + 8) /(x3 – 8).

151. y = x e 2x – 1.152. y = ln(x2 – 9).

153. y = (1 + x2) exp(-x2).154. y = lg(4 + x2).

155. y = exp(2/(1 – x)) .156. y = ln(16 – x2).

157. y = x2 + 1 + 2lnx.158. y = exp(1 + 4x – 2x2).

159. y = (2 + x) exp( - 4 - 4x - x2)).160. y = (1 – x) - 0.5 lg(1 – x).

161. -170. Составить уравнение касательной и нормали:

к графику кривой y = f(x) в точке, абсцисса которой равна x0;

к графику кривой x = x(t), y = y(t) в точке, для которой параметр t равен t0.

Построить графики кривых, касательных и нормалей. Для каждой кривой найти кривизну в указанных точках.

161.1) y = (9 – x2) /3, x0 = - 3/2; 2) x = 3cost, y =  3 sint, t0 = - /3.

162.1) y = 4 – 8x2, x0 = - 1/2; 2) x = 1/2 cost, y = 2 sint, t0 = 5/4.

163.1) y = 16 – 4x2, x0 = 1; 2) x = 2 sint, y =  4 cost, t0 = 5/6.

164.1) y = 8 – 3x2, x0 =  2; 2) x = 2 2/3 cost, y = 2 2 sint, t0 =  /6.

165.1) y = 25 – 5x2, x0 = 0.5 5; 2) x =  5 sint, y = 5 cost, t0 = 7/6.

166.1) y = (4 – x2) /2, x0 =  2; 2) x = 2sint, y =  2 cost, t0 = /4.

167.1) y = 8 – 4x2, x0 = 1; 2) x =  2 cost, y = 2 2 sint, t0 = /4

168.1) y = (7 – x2) /2, x0 = 0.5 7; 2) x =  7 cost, y = 7/2 sint, t0 = /3.

169.1) y = 2(4 – x2), x0 = 1; 2) x = 2 sint, y = 2 2 cost, t0 = 5/6.

170.1) y = 4 – 8x2, x0 = 1/2; 2) x = 1/ 2 cost, y = 2 sint, t0 = 5/4.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

171. -180. Даны функция u = f(x,y,z) и точки A(x0; y0; z0) и B(x1; y1; z1). Требуется:

вычислить значение u1 функции в точке В;

вычислить приближенное значение u1 функции в точке В, исходя из значения u0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом;

составить уравнение касательной плоскости к поверхности f(x,y,z) =C в точке А.

171. u = x2 + xyz + z2,A(1; 2; 1),B(1.05; 1.95; 0.96),C = 4.

172. u = x2z – xy + z2,A(1; 3; - 1),B(0.95; 3.08; - 0.96),C = - 3.

173. u = x2 + 2xz + y2z,A(4; 1; 0),B(4.1; 1.04; - 0.1),C = 16.

174. u = z2 – y2 + x + y + z,A(-2; 3; 1),B(-2.1; 3.1.1.05),C = - 6.

175. u = xy + yz + xz,A(2; 1; 2),B(1.96; 0.95; 2.1),C = 8.

176. u = x2 +y2 + z2 +x – z,A(1; - 1; 1),B(1.04; - 1.02; 0.95),C = 3.

177. u = 4 – xy2 +yz,A(-2; 1; 3),B(-2.1; 1.04; 3.1),C = 9.

178. u = x(y + z) – z2,A(-1; 2; 1),B(-0.95; 2.1; 0.95),C = - 4.

179. u = x2 – y2 + z2 + yz,A(1; 1; - 1),B(1.08; 0.92; - 1.08),C = 0.

180. u = 2x – z + 2y2 + xz,A(4; - 1; 1),B(3.95; - 1.05; 1.05),C = 13.

181. -190. Найти наименьшее и наибольшее значения функции

z = f(x; y) в области D, заданной системой неравенств. Сделать чертеж области D.

181. f(x; y) = x2 + 2y2 – 5xy,x  - 1,y  - 1,x + y  1.

182. f(x; y) = x2 – 3y2 + 6xy + 4,x + y  1.

183. f(x; y) = x2 + 2xy +3y + 4,y  5  x2,y  1.

184. f(x; y) = x2 + 2y2 – 2x – 4y + 5,1  x + y  2,x  0, y  0.

185. f(x; y) = 2y2 + 6xy – 13x +2,x  y2 + 1,y  (x – 1) /2.

186. f(x; y) = 2x2 + 2y2 – 10x + 13y + 1,x  2,y  - 3,y  x – 6.

187. f(x; y) = x2 + 3y2 + xy – 2x – y + 4,x - 1 + y  1.

188. f(x; y) = 2x2 + 2xy – 3y + 5,0  y  x2,x  1.

189. f(x; y) = 3x2 + 2y2 – 12x + 4y + 7,2  x – y  4,x  0, y  0.

190. f(x; y) = y2 + 2xy + 3x + 11,-3  x  - y2 + 1.

191. -200. Дано скалярное поле u = u(x,y). Требуется:

1) составить уравнение линии уровня u = C и построить эту линию; __

2) в точке А найти градиент и производную по направлению вектора АВ;

3) в точке А построить касательную и нормаль к линии уровня, получив их уравнения.

191. u = x2 + 4y2 + 4x + 4y,C = 13,A(1, - 2),B(2, 4).

192. u = x2 + 9y2 + 2x - 6y,C = 2,A(-1, 1),B(0, 4).

193. u = 4x2 + y2 + 4x - 4y,C = 36,A(2, - 2),B(1, 1).

194. u = 9x2 + y2 - 6x - 2y,C = 6,A(1, 3),B(3, 0).

195. u = x2 + 4y2 + 2x - 8y,C = 20,A(2, 3),B(1, 4).

196. u = 25x2 + y2 + 10x + 2y, C = 14,A(-1, - 1),B(2, 4).

197. u = 4x2 + 9y2 - 4x - 12y, C = 8,A(2, 0),B(-1, - 1).

198. u = 9x2 + 4y2 - 12x - 4y, C = 8,A(0, 2),B(2, 5).

199. u = x2 + 25y2 - 2x + 20y, C = 165,A(2, - 3),B(2, 1).

200. u = x2 + 4y2 + 2x - 4y,C = 35,A(5, 1),B(5, 4).

201. -210. Значения функции, полученные экспериментально, приведены в таблице. Методом наименьших квадратов найти наилучшую линейную аппроксимацию экспериментальной зависимости. На плоскости (x, y) построить полученную прямую и точки, заданные табл.1.

Таблица 1

201.	x	1.0	2.0	3.0	4.0	5.0	6.0	7.0	8.0
y	- 2.0	- 0.5	- 0.5	1.0	1.5	2.4	3.2	4.0
202.	x	1.0	2.0	3.0	4.0	5.0	6.0	7.0	8.0
y	6.0	4.5	4.5	2.8	1.0	-0.5	-1.5	-2.8
203.	x	0	1.0	2.0	3.0	4.0	5.0	6.0	7.0
y	- 5.0	- 4.0	-2.5	-2.5	-1.0	- 0.5	1.2	2.0
204.	x	0	1.0	2.0	3.0	4.0	5.0	6.0	7.0
y	6.5	5.2	3.5	3.5	1.6	0.2	- 1.5	- 2.5
205.	x	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8
y	- 0.2	0	0	0.1	0.15	0.25	0.3	0.4
206.	x	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8
y	0.6	0.45	0.4	0.3	0.1	- 0.1	- 0.2	- 0.3
207.	x	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7
y	- 0.5	- 0.4	- 0.25	- 0.25	- 0.1	0	0.1	0.2
208.	x	0	1.0	2.0	3.0	4.0	5.0	6.0	7.0
y	2.0	3.0	6.5	7.5	10	12.5	13.5	16.5
209.	x	1.0	2.0	3.0	4.0	5.0	6.0	7.0	8.0
y	2.0	0.5	0.5	-1.5	-1.5	-3.0	-4.2	-5.2
210.	x	0	0.2	0.4	0.6	0.8	1.0	1.2	1.4
y	- 4.0	-2.5	- 2.5	- 1.0	0.5	0.5	2.2	3.0

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

211. -220. Найти неопределенные интегралы.

211. а)  exp( - 8x3) x2 dx; б)  x tg2x dx; в)  (6x3 –7x2 – 3x) – 1 dx.

212. а)  tg(5x + 3) dx; б)  ln(x2 + 1) dx; в)  (x3 – 1) (4x3 – x) – 1 dx.

213. а)  ctg(2x–3) dx; б)  ln2x dx; в)  x2(x3+5x2+ 8x + 4) – 1dx.

214. а)  x – 1cos2(1 + lnx) dx; б)  arcsin2x dx; в)  (x3 + 1) (x3 – x2) – 1 dx.

215. а)  cos4x sin2x dx; б)  x2arctgx dx; в)  (x2 + 1) (x3+x2–x–1) –1dx.

____

216. а)  2x /1 –4x dx; б)  x – 2 ln 3x dx; в)  (x4+1) (x3–x2+x–1) – 1 dx.

_

217. а)  x (3x + 2) – 1 dx; б)  (1 – x) – 1/2arcsinx dx; в)  x (x3 – 3x + 2) - 1dx.

218. а)  ex(e2x + 4) – 1 dx; б)  x ln((1 + x) (1 – x) – 1) dx; в)  x (x3 - 1) - 1dx.

219. a) e – x(e2x–1) dx; б)  x-5/2 ln2x dx; в)  32x/((2x–1) (4x2 – 16x + 15)) dx

_

220. а)  (3x – 1) (x2 + 9) – 1 dx; б)  ex dx; в)  x2/(x3 + x2 + x + 1) dx.

221. -230. Вычислить несобственные интегралы или установить их расходимость.

11

221.  (x2 + 2x + 2) – 1 dx.222.  x - 2 (1 – x2) - 5/3 dx.223.  x lnx dx.

- 00



224.  x sinx dx.225.  x – 2 (x + 1) – 1 dx.

01

1 _1

226. (√x – 1) – 1 dx.227.  x3 exp( - x2) dx.228. (ex – cosx) –1 dx

000

1

229.  x (x + 1) – 3 dx.230.  x – 3/2 (1 –x) – 3/4 dx.

00

231. -240. Вычислить площадь фигуры, ограниченной линиями, уравнения которых даны.

231. y = 1/(1 + x2), y = x2/2.232. y = x2,y = x3/3.

233. y = ex, y = e – x, x = 1.234. y2 = 2x + 1, x – y – 1 = 0.

235. y2 + 8x = 16, y2 – 24x = 48.236. y = x(x – 1) 2, y = 0.

237. (y – x – 2) 2 = 9x, x = 0, y = 0.238. y = (x2 + 2x) e – x, y = 0.

239. x = y2(y – 1), x = 0.240. y = x – x5/2, y = 0.

241. -250. Вычислить длины дуг кривых, заданных следующими уравнениями.

241. y = x2/4 – 0,5lnx,1  x  2.

242. x = 5(t – sint), y = 5(1 – cost),0  t  .

_

243.  = 2e, - /2    /2.244. y = - ln cosx,0x/6.

245. x = 3(2cost – cos2t),y = 3(2sint – sin2t),0  t  2.

246.  = 1 - sin, - /2    - /6.247. y = ln(x2 – 1),2  x  3.

248. x = 4(cost + t sint),y = 4(sint – t cost),0  t  2.

249.  = 8cos,0    /4.250. y = (e2x+e-2x+3) /4,0  x  2.

Дифференциальные уравнения

251. -260. Найти общее решение дифференциального уравнения.

251. xy'-2y=x3ex.252. (x+1) y'-2y=(x+1) 4.

253. x2y'+2xy=cosx.254. xy'+y=x+1.

255. y'cosx - ysinx=4x3.256. y'-ycosx= exp(sinx).

257. x2 y'+2xy=1.258. y'+2xy=2x exp(-x2).

259.2xy'-y=2x3/2cosx.260. y'+ytgx=2xcosx.

261. -270. Найти общее решение дифференциального уравнения.

261. y"y3=1.262. y"'=(y") 3.

263. y" (x-1) - y'=x(x-1) 2.264. (1+x2) y"+1+(y') 2=0.

265. yy"+(y') 2=0.266. xy"=y'ln(y'/x).

267. (1-x2) y"=xy'.268. y"x+y'=x2.

269. xy"'+y"=1+x.270. y"=-(x/y').

271. -280. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.

271. y"-9y=e-2x; y(0) =0,y'(0) =0.

272. y"-4y=x-1; y(0) =0,y'(0) =0.

273. y"+2y'+y=cosx; y(0) =0,y'(0) =0.

274. y"+3y'+2y=1+x+x2; y(0) =0,y'(0) =1.

275. y"+2y'+5y=13e2x; y(0) =1,y'(0) =4.

276. y"+2y'-8y=16x+4; y(0) =2,y'(0) =6.

277. y"+4y'-12y=8sin2x; y(0) =0,y'(0) =0.

278. y"-4y'+13y=26x+5; y(0) =1,y'(0) =0.

279. y"+y=cos3x; y(/2) =4,y'(/2) =1.

280. y"-4y'+3y=e5x; y(0) =3,y'(0) =9.

281. -290. Найти общее решение системы дифференциальных уравнений с помощью характеристического уравнения.

281. x1'+x1-3x2=0, x2'-2x1=0.282. x1'-4x1+x2=0, x2'+2x1-5x2=0.

283. x1'-x1+2x2=0, x2'+3x1-6x2=0.284. x1'+5x1+4x2=0, x2'+2x1+3x2=0.

285. x1'-6x1-3x2=0, x2'+8x1+5x2=0.286. x1'-3x1+2x2=0, x2'-2x1-8x2=0.

287. x1'+5x1+8x2=0, x1'+3x1+3x2=0.288. x1'-x1+x2=0, x2'-x1-x2=0.

289. x1'+4x1-x2=0, x2'+2x1+x2=0.290. x1'+x2=0, x2'-2x1-2x2=0.

Найти интегральную кривую уравнения y"-k2y=0 (k0), которая касается прямой y-y0=a(x-x0) в точке (x0, y0).

Тело массой m падает с высоты h под действием силы тяжести и силы сопротивления, пропорциональной скорости с коэффициентом k. Начальная скорость тела равна нулю. Найти закон движения тела.

Тело массой m скользит по горизонтальной плоскости под действием толчка, давшего начальную скорость V0. На тело действует сила трения, равная –km. Найти расстояние, которое тело пройдет до полной остановки.

Найти интегральную кривую уравнения y"+k2y=0 (k0), касающуюся прямой y-y0=a(x-x0) в точке (x0, y0).

Найти уравнение кривой, у которой отрезок касательной, заключенный между осями координат, делится пополам в точке касания. Кривая проходит через точку (2; 1).

Материальная точка массы m перемещается по прямой под влиянием внешней силы F=Asint и восстанавливающей силы, которая направлена к началу отсчета перемещений и прямо пропорциональна расстоянию точки от начала отсчета с коэффициентом k=4mω2. Сопротивление среды отсутствует. Определить закон движения материальной точки, если при t=0 она находилась в начале отсчета с нулевой скоростью.

Найти уравнение кривой, подкасательная которой имеет постоянную длину a. Кривая проходит через точку (a; e).

Найти уравнение кривой, проходящей через точку (3; 1), если отрезок касательной к кривой, заключенный между точкой касания и осью Ox делится пополам в точке пересечения с осью Oy.

Найти уравнение кривой, у которой сумма координат точки касания равна удвоенной подкасательной. Кривая проходит через точку (1; 1).

Найти интегральную кривую уравнения ysinx=ylny, проходящую через точку (/2; 1).

ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ

301. -310. Исследовать на сходимость ряд.



301.  1/(n – cos26n).302.  (n!) 2/ [(3n + 1) (2n) !]

n=1n=1



303.  (2n + cos n) /(3n + sin n).304.  (3n + 2) ! /(10nn2).

n=1n=1



305.  ln [(n2+1) /(n2 + n + 1)].306.  (n! n⅓) /(3n + 2).

n=1n=1



307.  [4n – 1 (n2 + 5) ½] / [(n–1) !].308.  (3 + 7n) /(5n + n).

n=1n=1



 n sin(n – 4/3).310.  [n! (2n + 1) !] / [(3n) !]

n=1n=1

311. -320. Исследовать на абсолютную и условную сходимость ряды.

311. .312.

313. 314.

315. 316.

317. 318.

319. 320.

321. -330. Разложить функцию f(x) в ряд по степеням x.

321. 322.

323. 324.

325. 326.

327. 328.

329. 330.

331. -340. Разложить в ряд Фурье в указанном интервале функцию f(x). Построить график этой функции и график суммы полученного ряда Фурье.

331. в интервале ( - 1, 1).

332. в интервале (0, 3) по синусам.

333. в интервале (-, ).

334. в интервале (-, ).

-/2,x(-, 0),

335.  0,x = 0,

 /4,x (0, ) в интервале (-, ).

336. в интервале (-2, 2).

337. в интервале (0, 2) по косинусам.

338. /4 – x/2в интервале (0, ) по синусам.

339. в интервале (-, ).

340. ( – x) /2в интервале (0, ) по синусам.

КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

341. -350. С помощью двойного интеграла найти площадь фигуры, ограниченной заданными кривыми.

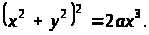
351. -360. С помощью двойного интеграла найти объем тела, ограниченного поверхностями, уравнения которых заданы.

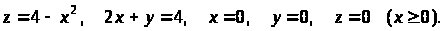
361. -370. Вычислить тройной интеграл по области V, ограниченной заданными поверхностями.

371. -380. Вычислить криволинейный интеграл второго рода вдоль заданной линии (для незамкнутых кривых направление обхода соответствует возрастанию параметра t или переменной x; для замкнутых кривых направление предполагается положительным).

L– отрезок прямой, от точки (0; 0) до (; 2).

L – дуга линии от точки (0; 0) до точки (1; 1).

L – дуга линии от точки (0; 0) до точки (1; 1).

L– дуга окружности

L – эллипс

L - дуга окружности

L – линия , x [-1; 1].

L – линия y = 1 - |1-x|, x [0; 2].

L– арка циклоиды

L - окружность x2 + y2 = R2.

381. -390. Дано скалярное поле и векторное поле . Найти , и в точке .

.

.

.

.

.

.

391. -400. Найти поток векторного поля через часть плоскости , расположенную в первом октанте (нормаль образует острый угол с осью ).

401. -410. Доказать потенциальность поля и найти его потенциал .

СПЕЦИАЛЬНЫЕ РАЗДЕЛЫ

411. -420. Восстановить аналитическую функцию f(z) = u + iv по заданной действительной или мнимой части.

411. .412. .

413. .414. .

415. .416. .

417. .418. .

419. .420. .

421. -430. Используя теорию вычетов, вычислить интегралы.

421. .422. .

423. .424. .

425. .426. ; .

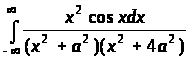427. ; .428. .

429. . .430. ; , .

431. -440. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.

431. x + 2x –3x = e - t,x(0) = 0,x(0) = 1.

432. x + 2x = t sin t,x(0) = 0,x(0) = 0.

433. x + 2x + x = sin t,x(0) = 0,x(0) = - 1.

434. x + 2x + x = t2,x(0) = 1,x(0) = 0.

435. x + 2x + 2x =1,x(0) = 0,x(0) = 0.

436. x + x = cos t,x(0) = 2,x(0) = 0.

437. x - 2x +5 x = 1 - t,x(0) = 0,x(0) = 0.

438. x + 2x + x = t,x(0) = 0,x(0) = 0.

439. x - 2x + x = t – sin t,x(0) = 0,x(0) = 0.

440. x + x = t cos2t,x(0) = 0,x(0) = 0.

441. -450. Найти все особые точки функции и определить их характер. Разложить в ряд Лорана в указанном кольце.

441. .

442. .

443. .

444.

445.

446.

447.

448. .

449.

450. .

451. -460. Однородный упругий стержень длины l изготовлен из материала с плотностью  и модулем упругости E. Стержень имеет постоянное поперечное сечение площади S. Найти методом Фурье решение уравнения продольных колебаний стержня

2u/t2 =a2 2u/x2,a2 = E/.

при заданных начальных и граничных условиях.

451. u(x,0) = Px/ES, u(x,0) /t = 0; u(0,t) = 0, u(l,t) /x = 0.

452. u(x,0) = 0, u(x,0) /t = 0; u(0,t) = 0, u(l,t) /x = P/ES.

453. u(x,0) = 0, u(x,0) /t = 0; u(0,t) /x = P/ES, u(l,t) /x = P/ES.

454. u(x,0) = - P(l-x) /ES, u(x,0) /t = 0; u(0,t) /x = 0, u(l,t) = 0.

455. u(x,0) = 0, u(x,0) /t = 0; u(0,t) = P/ES, u(l,t) = 0.

456. u(x,0) = 0, u(x,0) /t = 0; u(0,t) = 0, u(l,t) = Vt.

457. u(x,0) = 0, u(x,0) /t = 0; u(0,t) = - Vt, u(l,t) = 0.

458. u(x,0) = 0, u(x,0) /t = 0; u(0,t) = 0, u(l,t) = A sin(t).

459. u(x,0) = 0, u(x,0) /t = 0; u(0,t) = 0, u(l,t) /x = (P/ES) sin(t).

460. u(x,0) = 0, u(x,0) /t = 0; u(0,t) /x = (P/ES) sin(t), u(l,t) = 0.

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

461. Три стрелка стреляют по цели. Вероятность попадания в цель первым стрелком равна 0.7, вторым стрелком – 0.8, третьим стрелком – 0.9. Определить вероятность, что в цель попадает только один из стрелков.

462. В ящике 10 деталей, из которых 4 окрашены. Сборщик наудачу взял 3 детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.

463. В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность (если считать выбор случайным), что выбраны: 1) два мальчика; 2) две девочки?

464. Отдел технического контроля проверяет изделие на стандартность. Вероятность того, что изделие стандартно, равна 0.9. Найти вероятность того, что из двух проверенных изделий только одно стандартное.

465. Вероятность того, что при одном измерении некоторой физической величины ошибка превысит допустимое значение, равна 0.4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них ошибка превысит допустимое значение.

466. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0.8. Найти вероятность того, что из трех проверенных изделий только два изделия высшего сорта.

467. Студент разыскивает нужную формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором, третьем справочнике, соответственно равны 0.6, 0.7, 0.8. Найти вероятность того, что формула содержится только в двух справочниках.

468. Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем, четвертом ящике, соответственно равны 0.6, 0.7, 0.8, 0.9. Найти вероятность того, что деталь содержится не более чем в трех ящиках.

469. В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в переплете. Библиотекарь наугад взял 2 учебника. Найти вероятность того, что оба учебника окажутся в переплете.

470. В лотерее 100 билетов: среди них один выигрыш в 5000 руб., 3 выигрыша по 2500 руб., 15 выигрышей по 300 руб. Некто покупает один билет. Найти вероятность: а) выиграть не менее 2500 руб., б) выиграть не более 2500 руб.

471. Два автомата производят одинаковые детали. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит 60% деталей отличного качества, а второй – 84%. Наудачу взятая деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.

Число грузовых машин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе, как 3: 2. Вероятность того, что будет заправляться грузовая машина, равна 0.1, для легковой машины эта вероятность равна 0.2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.

473. В специализированную больницу поступают в среднем 50% больных с заболеванием «К», 30% - с заболеванием «М», 20% - с заболеванием «П». Вероятность полного излечения болезни «К» равна 0.7; для болезней «М» и «П» эти вероятности соответственно равны 0.8 и 0.9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием «К».

474. С первого автомата на сборку поступает 20%, со второго – 30%, с третьего – 50% деталей. Первый автомат дает в среднем 0.2% брака, второй – 0.3%, третий - 0.1%. Найти вероятность того, что деталь, изготовлена на первом автомате.

475.60% учащихся – мальчики.80% мальчиков и 75% девочек имеют билеты на школьный вечер. В школьное бюро находок принесли кем-то потерянный билет. Какова вероятность того, что он принадлежал девочке?

476. Трое охотников одновременно выстрелили по кабану, который был убит одной пулей. Определить вероятность того, что кабан был убит первым охотником, если вероятности попадания для каждого охотника соответственно равны 0.2, 0.4, 0.6.

477. В группе из 10 студентов, пришедших на экзамен, трое подготовленных отлично, 4 – хорошо, 2 – посредственно, 1 – плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20, хорошо подготовленный – на 16, посредственно – на 10, плохо – на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что студент подготовлен отлично.

478. В ящике лежат 20 теннисных мячей, в том числе 12 новых и 8 игранных. Из ящика извлекают наугад два мяча для игры и после игры возвращаются в ящик. После этого из ящика вынимают два мяча для следующей игры. Найти вероятность того, что эти оба мяча будут неигранными.

479. На сборку поступают детали с двух автоматов. Первый дает 0.2% брака, второй – 0.1%. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 2000 деталей, а со второго – 3000 деталей.

480. Имеются три урны: в первой из них 5 белых шаров и 3 черных; во второй 4 белых шара и 6 черных; в третьей – 8 белых шаров (черных нет). Из выбранной наугад урны извлекается один шар. Этот шар оказался белым. Найти вероятность того, что шар извлекался из первой урны.

481. -490. Для случайной величины X построить ряд распределения и функцию распределения. Найти ее математическое ожидание, дисперсию, начальный момент второго порядка и третий центральный момент:

481. Стрелок делает по мишени 3 выстрела. Вероятность попадания в мишень при каждом выстреле равна 0.3. Случайная величина X – число попаданий в мишень.

482. Опыт состоит из трех независимых бросаний монеты. Случайная величина X – число появлений герба.

483. Проводится 3 независимых опыта, в каждом из которых событие А может появиться с вероятностью 0.4. Случайная величина X – число появлений события А.

484. Игральную кость бросают 4 раза. Случайная величина X – число выпаданий шестерки.

Производится три независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 0.7. Случайная величина X – число попаданий в мишень.

486. Имеются три лампочки, каждая из которых с вероятностью 0.1 имеет дефект. При включении дефектная лампочка сразу же перегорает, после чего ее заменяют другой. Случайная величина X – число лампочек, которое будет испробовано.

487. Охотник стреляет до первого попадания, но успевает сделать не более четырех выстрелов. Вероятность попадания при каждом выстреле равна 0.7. Случайная величина X – число выстрелов, произведенных охотником.

488. Два стрелка делают по выстрелу в одну мишень. Вероятность попадания в нее первым стрелком равна 0.3, вторым – 0.6. Случайная величина X – число попаданий в мишень.

489. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0.1. Случайная величина X – число отказавших элементов в одном опыте.

490. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Случайная величина X – число стандартных деталей среди отобранных.

491. -500. Для случайной величины X с заданной функцией распределения F(x) требуется найти: а) плотность вероятности; б) математическое ожидание и дисперсию; в) построить графики функции распределения и плотности вероятности случайной величины X:

491.0 при x  1

F(x) = (x + 1) /2 при 1  x  1

1 при x  1

492.0 при x  0

F(x) = sin x при 0  x  /2

1 при x  /2

493.0 при x  0

F(x) = x /3 при 0  x  3

1 при x  3

494.0 при x  1

F(x) = (x - 1) /2 при 1  x  3

1 при x  3

495.0 при x  0

F(x) = x /4 при 0  x  4

1 при x  4

496.0 при x  1

F(x) = (x + 1) /2 при 1  x  1

1 при x  1

497.0 при x  0

F(x) = x /5 при 0  x  5

1 при x  5

498.0 при x  - /2

F(x) = cos x при /2  x  0

1 при x  0

499.0 при x  0

F(x) = x 2/4 при 0  x  2

1 при x  2

500.0 при x  0

F(x) = x 2/9 при 0  x  3

1 при x  3

501. -510. По приведенной в табл.2 выборке нормально распределенной случайной величины X следует

найти точечные оценки математического ожидания, дисперсии и среднего квадратического отклонения:

записать плотность вероятности и функцию распределения случайной величины X;

найти доверительный интервал (с надежностью  = 0.95) для математического ожидания, считая, что дисперсия известна и равна полученной в п.1 точечной оценке;

вычислить P( X  ).

514. -520. Результаты наблюдений над двумерной случайной величиной (X,Y) приведены в табл.3. Требуется построить корреляционное поле и подобрать регрессионную зависимость Y от X (рекомендуется использовать модель линейной регрессии).

Таблица 2.

			x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12
501.	2.5	3.5	0.2	1.8	3.4	3.6	2.8	4.4	5.0	4.4	1.8	2.8	3.3	3.4
502.	2	4	0.58	2.80	5.40	6.08	3.25	1.42	5.10	3.10	4.09	4.02	6.12	2.84
503.	5	10	10.9	10.6	9.9	11.0	10.5	10.8	10.7	10.1	10.5	11.1	11.2	10.4
504.	1.0	1.8	1.85	1.36	0.32	0.90	1.70	2.40	1.60	1.42	0.98	1.42	0.98	1.02
505.	7	13	1.0	2.6	1.8	10.8	15.0	0.8	3.3	3.8	4.8	6.8	13.8	0.0
506.	0.77	0.79	0.795	0.792	0.780	0.783	0.781	0.769	0.779	0.786	0.788	0.778	----	----
507.	0. 195	0.210	0. 202	0.215	0. 201	0. 209	0. 198	0.214	0. 190	0. 209	0. 198	0. 208	0.189	0. 192
508.	30.5	35.5	25.5	32.7	35.5	30.7	30.3	29.3	27.3	30.5	31.3	32.5	35.5	31.1
509.	1.345	1.350	1.347	1.344	1.347	1.343	1.345	1.343	1.342	1.348	1.346	1.345	----	----
510.	33	36	33.6	33.6	33.2	34.0	34.1	34.2	32.3	32.5	33.2	33.4	33.2	33.5

Таблица 3.

	1	2	3	4	5	6	7	8	9	10	11	12
511 x y	1.50 8.8	1.55 8.2	1.60 7.2	1.65 6.7	1.70 6.3	1.75 6.3	1.80 6.0	1.85 5.3	1.90 4.7	1.95 4.3	----	----
512 x y	0.5 0.67	0.6 0.69	0.7 0.71	0.8 0.74	0.9 0.76	1.0 0.80	1.1 0.82	1.2 0.87	1.3 0.97	1.4 1.03	----	----
513 x y	3.5 3.3	3.6 3.4	3.7 3.5	3.9 3.4	4.0 3.8	4.1 3.7	4.2 3.8	4.3 4.1	4.4 4.2	4.5 4.1	4.6 4.2	4.7 4.5
514 x y	15 2.8	20 2.6	25 4.6	30 4.5	35 6.4	40 6.6	45 6.6	50 9.6	55 9.6	60 8.2	----	----
515 x y	25 2.5	26 1.9	35 5.1	37 3.8	43 6.1	50 6.9	54 8.5	59 7.4	65 12.1	75 14.4	----	----
516 x y	2.9 1.71	4.8 1.63	6.5 1.34	8.1 1.32	9.4 0.96	10.6 0.97	12.0 0.60	13.4 0.57	14.7 0.56	----	----	----
517 x y	3.1 2.00	3.7 1.94	4.1 1.95	4.6 1.83	5.3 1.85	5.7 1.72	6.1 1.75	6.5 1.70	7.1 1.62	7.6 1.68	8.1 1.45	9.1 1.43
518 x y	5 4	7.5 4	10 11	12.5 15	15 16	17.5 24	20 26	22.5 32	25 33	27.5 42	30 45	32.5 47
519 x y	3 4.5	3.5 5	4 5.2	4.5 5.9	5 6.7	5.5 7.2	6 7.7	6.5 9.3	7 8.8	7.5 9.1	8 9.5	----
520 x y	0 5.13	10 5.32	20 5.54	30 5.76	40 5.99	50 6.25	60 6.47	70 6.70	80 6.90	90 7.12	100 7.36	110 7.61

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Высш. шк., 1998. – 320 с.

2. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1986. – 224 с.

3. Сборник задач по математике для втузов. В 4 ч. Ч.1. Линейная алгебра и основы математического анализа / Под общ. ред. А.В. Ефимова и Б.П. Демидовича. – М.: Наука, 1993. – 480 с.

4. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. В 2 т. Т.1. – М.: Наука, 1976. – 456 с.

5. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. В 2 т. Т.2. – М.: Наука, 1985. – 560 с.

6. Кудрявцев Л.Д. Курс математического анализа. В 2 т. Т.1. – М.: Высш. шк., 1988. – 712 с.

7. Кудрявцев Л.Д. Курс математического анализа. В 2 т. Т.2. – М.: Высш. шк., 1988. – 576 с.

8. Задачи и упражнения по математическому анализу для втузов / Под ред. Б.П. Демидовича. – М.: Наука, 1978. – 480 с.

9. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1. – М.: Высш. шк., 1996. – 304 с.

10. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2. – М.: Высш. шк., 1996. – 576 с.

11. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высш. шк., 1998. – 479 с.

12. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высш. шк., 1998. – 400 с.

13. Сборник задач по математике для втузов. В 4 ч. Ч.4. Методы оптимизации. Уравнения в частных производных. Интегральные уравнения / Под. ред. А.В. Ефимова. – М.: Наука, 1993. – 304 с.