Компактные операторы
Содержание
Введение 3
§1. Основные понятия и определения 4
1.1. Линейные пространства 4
1.2. Нормированные пространства 5
1.3. Банаховы пространства 6
1.4. Компактные множества 8
1.5. Линейные операторы и линейные функционалы 11
1.6. Сопряженные операторы 12
§2. Компактные операторы 13
2.1. Определение компактного оператора 13
2.2. Свойства компактных операторов 13
2.3. Примеры некомпактного и компактных операторов 16
Литература 20
Введение
Изучение произвольных линейных операторов представляет собой весьма трудоемкую задачу, однако среди линейных операторов можно выделить классы операторов, которые могут быть рассмотрены более подробно. Данная работа рассматривает основные понятия, свойства, определения и теоремы, связанные с одним из классов линейных операторов – компактными операторами.
Работа состоит из двух параграфов. Первый из них содержит предварительные сведения, необходимые для рассмотрения темы: понятия пространств, которые необходимы при изучении компактных операторов, понятия линейного оператора и линейного функционала, сопряженного оператора, компактного множества. Во втором параграфе рассмотрено определение компактного оператора, основные свойства этого класса операторов и примеры компактных и некомпактного оператора.
§1. Основные понятия и определения.
1.1 Линейные пространства.
Определение:
Непустое множество
элементов называется линейным, если
оно удовлетворяет таким условиям:
I.
Для
любых двух элементов
определен единственный элемент
,
называемый суммой и обозначаемый
,
причем
1)
;
2)
;
3) в
существует
такой элемент 0, что
для всех
;
4) для каждого
существует
такой элемент
,
что
.
II. Для
любого числа
и любого элемента
определен элемент
,
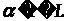причем
1)
;
2)
;
3)
;
4)
;
([1], стр. 120).
Примеры линейных пространств
1. Пространство действительных
чисел
является линейным пространством по
операциям сложения и умножения.
2.
– пространство, элементами которого
являются последовательности чисел
,
удовлетворяющих условию
с операциями
,
([1], стр. 121).
1.2 Нормированные пространства
Определение:
Множество
называется нормированным пространством,
если:
1)
– линейное пространство над полем
действительных или комплексных чисел.
2) Для каждого элемента
определено вещественное число, называемое
его нормой и обозначаемое
,
и выполнены условия:
а)
для
любого
;
б)
для любого
и любого
;
в)
,
для любых
([1], стр. 138).
Примеры нормированных пространств:
1. Пространство
становится нормированным, если положить
.
2. Пространство
с элементами
нормировано, при условии
.
3. Пространство
функций, непрерывных на отрезке
,
нормировано, если взять
.
([1], стр. 139).
1.3 Банаховы пространства
Определение:
Расстоянием (метрикой) между двумя
элементами
и
называется вещественное неотрицательное
число, обозначаемое
и подчиненное трем аксиомам:
1)
;
2)
;
3)
;
Определение:
Последовательность
точек метрического пространства
называется фундаментальной, если
при
.
Справедливы утверждения:
Если последовательность
сходится к некоторому пределу, то она
фундаментальна.
Доказательство:
Пусть
,
тогда
,
при
Всякая фундаментальная
последовательность
ограничена.
Определим расстояние в нормированном
пространстве
,
полагая для любых
.
Тогда
означает, что
.
Это сходимость по норме.
Фундаментальная последовательность
в нормированном пространстве в
соответствии с определением расстояния
характеризуется условием
,
при
Определение: Нормированное пространство называется полным, если всякая фундаментальная последовательность его элементов имеет предел.
Определение: Полное нормированное пространство называется банаховым пространством.
([2], стр. 137)
1.4 Компактные множества
Определение:
Множество
в метрическом пространстве
называется компактным, если из всякой
бесконечной последовательности
можно выделить подпоследовательность,
сходящуюся к некоторому пределу
.
Определение:
Множество
,
лежащее в некотором метрическом
пространстве
,
называется предкомпактным, или
относительно компактным (компактным
относительно),
если его замыкание в
компактно.
Определение:
Множество
называется ограниченным, если оно
содержится в некотором шаре с центром
в точке
,
то есть существует такая постоянная
,
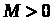такая, что для любого
выполняется неравенство
В курсе теории метрических пространств доказывалось, что любое компактное множество является ограниченным. Докажем, что любое относительно компактное множество также является ограниченным.
Теорема: Множество
,
лежащее в некотором метрическом
пространстве
,
и относительно компактное, является
ограниченным.
Доказательство. Замыкание
множества М является компактным,
следовательно, ограниченным. Но
,
а подмножество ограниченного множества
также ограничено.
В конечномерном пространстве
выполняется также обратное утверждение.
Теорема: В
конечномерном пространстве
всякое ограниченное подмножество
относительно компактно.
Эта теорема
следует из теоремы Больцано-Вейерштрасса
для пространства
:
в этом пространстве всякая ограниченная
последовательность содержит сходящуюся
подпоследовательность.
Можно доказать также более общую теорему.
Теорема: В конечномерном нормированном пространстве всякое ограниченное подмножество относительно компактно.
Доказательство:
Пусть
– ограниченное подмножество n–мерного
пространства
,
т. е. существует такая константа
,
что
для всех
.
Каждому
сопоставляем вектор
,
координаты которого
равны соответствующим координатам в
разложении элемента
по некоторому фиксированному базису.
Тогда справедливо следующее неравенство:
(1), где
–
наименьшее значение
на единичном шаре
,
.
Возьмем любую последовательность
.
По неравенству (1) соответствующие этим
элементам векторы
образуют ограниченное множество, а в
ограниченные множества относительно
компактны, следовательно, из
последовательности
,
можно выделить частичную
,
сходящуюся к некоторому пределу.
Сходимость в
есть сходимость по координатам,
следовательно, и последовательность
сходится по координатам. Но тогда эта
последовательность сходится к некоторому
пределу и по норме (в силу непрерывности
суммы и произведения в нормированных
пространствах). Тем самым относительная
компактность
доказана.
Определение:
Семейство
функций называется равностепенно
непрерывным, если для любого
найдется такое 
,
что
,
для любой функции
,
для любых
,
таких, что
.
Определение:
Семейство
функций
,
определенных на некотором отрезке,
называется равномерно ограниченным,
если существует такое число
,
что
,
для любого
Теорема Арцела:
Для того чтобы семейство
непрерывных функций, определенных на
отрезке
,
было предкомпактно в
,
необходимо и достаточно, чтобы это
семейство было равномерно ограничено
и равностепенно непрерывно.
Теорема: Образом компактного множества при непрерывном отображении является компактное множество.
Докажем аналогичную теорему для относительно компактных множеств.
Теорема: Образом относительно компактного множества при непрерывном отображении является относительно компактное множество.
Доказательство.
Пусть
– непрерывное отображение,
– относительно компактное множество.
Рассмотрим последовательность точек
из множества
:
,
.
Так как множество
относительно компактно, то существует
подпоследовательность
.
Так как отображение
– непрерывное, то
.
Значит, для множества
выполнено условие относительной
компактности.
Примеры компактных и некомпактных множеств
В пространстве
всякий отрезок
будет компактен. (Так как пространство
конечномерно, а данный отрезок является
замкнутым и ограниченным множеством).
В пространстве
шар с центром в
и радиусом
,
то есть множество точек
,
таких, что
,
является компактным. (Аналогично по
доказанной теореме).
В пространстве
множество
будет компактным, поскольку какую бы
мы ни взяли бесконечную последовательность
его элементов, из неё всегда можно будет
выделить подпоследовательность,
состоящую из одного элемента множества,
которая, очевидно, будет сходящейся к
этому элементу множества (определение).
В пространстве
рассмотрим множество элементов
,
,
… (у последовательности
единица стоит на
–м
месте, а на остальных местах нули). Оно
ограничено и замкнуто, но никакая
подпоследовательность последовательности
не фундаментальна и, значит, не сходится,
поскольку
при
.
Множество некомпактно.
1.5 Линейные операторы и линейные функционалы
Пусть
– линейные нормированные пространства.
Определение:
Линейным оператором, действующим из
в
,
называется отображение
,
удовлетворяющее условию:
для любых
,
.
Будем говорить, что в
(вещественной или комплексной линейной
системе) определен функционал
,
если каждому элементу
поставлено в соответствие некоторое
вещественное (комплексное) число
.
Определение: Линейный оператор, действующий из Е в Е>1>, называется ограниченным, если он определен на всем Е и каждое ограниченное множество переводит снова в ограниченное.
Определение:
Оператор А называется непрерывным
в точке
,
если для любой последовательности
выполняется условие
.
Определение: Оператор А называется непрерывным, если он непрерывен в каждой точке пространства Е.
Теорема: Для того,
чтобы линейный оператор
был непрерывным,
необходимо и достаточно, чтобы он был
ограничен.
Доказательство.
1. Пусть оператор А
неограничен. Тогда существует М
Е
– ограниченное множество,
такое, что множество АМЕ>1>
не ограничено. Следовательно,
в Е>1>
найдется такая окрестность нуля V,
что ни одно из множеств
АМ
не содержится в V.
Но тогда существует такая последовательность
х>n>>
>M
, что ни один из элементов
Ах>n>
не принадлежит V
и получаем, что
в Е, но
не сходится к 0 в Е;
это противоречит непрерывности оператора
А.
2. Если оператор А
не непрерывен в точке 0, то в Е>1>
существует такая последовательность
,
что Ах>n>
не стремится к 0.
При этом последовательность
ограничена, а последовательность
не ограничена. Итак, если оператор А
не непрерывен, то А и
не ограничен.
Определение: Оператор называется конечномерным, если он ограничен и переводит данное пространство в конечномерное.
Определение:
Функционал
называется линейным, если
Линейный функционал – это частный случай линейного оператора.
([1], стр. 217), ([1], стр. 125)
Примеры линейных функционалов:
Пусть
–
мерное арифметическое пространство с
элементами
и
– произвольный набор из
–
фиксированных чисел. Тогда
является линейным функционалом.
Пример линейного функционала
в
Пусть
– фиксированное целое положительное
число. Для каждого
из
положим
.
Таким образом
является линейным функционалом в
.
1.6. Сопряженные операторы
Определение:
Совокупность всех непрерывных линейных
функционалов, определенных на некотором
линейном нормированном пространстве
,
образует линейное пространство, которое
называется пространством, сопряженным
с
,
и обозначается
Рассмотрим непрерывный линейный
оператор
,
отображающий линейное топологическое
пространство
в такое же пространство
.
Пусть
– линейный функционал, определенный
на
,
т. е.
.
Применим функционал
к элементу
.
Функционал
есть непрерывный линейный функционал,
определенный на
.
Обозначим его через
.
Функционал
есть, таким образом, элемент пространства
(сопряженное с
).
Каждому функционалу
мы поставили в соответствие функционал
,
т.е. получили некоторый оператор,
отображающий
в
.
Этот оператор называется сопряженным
к оператору
и обозначается
.
Обозначив значение функционала
на элементе
символом
,
получим, что
,
или
.
Это соотношение можно принять за определение сопряженного оператора. ([1], стр. 229)
§2. Компактные операторы
2.1 Определение компактного оператора
Определение:
Оператор
,
отображающий банахово пространство
в себя (или другое банахово пространство),
называется компактным (вполне непрерывным),
если он каждое ограниченное множество
переводит в предкомпактное. ([1], стр.235).
Данное определение можно сформулировать в силу первого определения компактного множества следующим образом:
Определение: Пусть
дан линейный оператор
.
Если он переводит любую ограниченную
последовательность
в
,
причем в
можно выделить сходящуюся
подпоследовательность, то такой оператор
будем называть компактным.
Свойства компактных операторов
Из определения компактного оператора и ограниченности относительно компактного множества следует, что любой линейный компактной оператор является ограниченным, следовательно, непрерывным.
Если
– компактный оператор,
– ограниченный, то операторы
и
– компактные.
Доказательство.
Если множество
ограничено, то множество
тоже ограничено. Следовательно, множество
относительно компактно, а это и означает,
что оператор
вполне непрерывен. Далее, если
ограничено, то
относительно компактно, а тогда в силу
непрерывности
множество
тоже относительно компактно, то есть
оператор
вполне непрерывен. Теорема доказана.
([1], стр.241).
Если операторы
и
компактные, действующие из нормированного
пространства
в нормированное пространство
и
– любые числа, то оператор
также компактен.
Доказательство.
Пусть множество
ограничено. В его образе
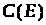возьмем произвольную последовательность
элементов
.
Тогда существуют
,
при которых
.
Положим
.
При этом
.
Так как множество
компактно, а
,
то существует подпоследовательность
,
имеющая предел. Аналогично в компактном
множестве
из последовательности
можно выделить подпоследовательность
,
имеющую предел. Но так как вместе с
сходится и последовательность
,
то существует
,
что и доказывает компактность множества
,
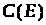а, следовательно, оператор
компактен. ([2], стр.306).
Если
– последовательность компактных
операторов в банаховом пространстве
,
сходящаяся по норме к некоторому
оператору
,
то оператор
тоже компактен.
Доказательство.
Для установления компактности оператора
достаточно показать, что, какова бы ни
была ограниченная последовательность
элементов из
,
из последовательности
можно выделить сходящуюся
подпоследовательность.
Так как оператор
компактен, то из последовательности.
можно выбрать сходящуюся подпоследовательность.
Пусть
(2) – такая подпоследовательность, что
сходится.
Рассмотрим теперь последовательность
.
Из неё тоже можно выбрать сходящуюся
подпоследовательность. Пусть
такая подпоследовательность выбранная
из (2), что
сходится. При этом, очевидно, что
тоже
сходится. Рассуждая аналогично, выберем
из последовательности
такую подпоследовательность
,
что
сходится и т.д. Затем возьмем диагональную
последовательность
.
Каждый из операторов
переводит её в сходящуюся. Покажем, что
и оператор
тоже переводит её в сходящуюся. Тем
самым мы покажем, что
компактен. Так как пространство
полно, то достаточно показать, что
– фундаментальная последовательность.
Имеем
.
Пусть
,
выберем сначала
так, что
,
а потом выберем такое
,
чтобы при всех
и
выполнялось неравенство
(это возможно, так как последовательность
сходится). При этих условиях из
предпоследнего неравенства получаем,
что
для всех достаточно больших
и
.
Таким образом свойство доказано. ([1],
стр. 239).
Оператор, сопряженный компактному оператору, компактен ([1], стр.241).
Примеры некомпактного и компактных операторов
Пусть
– единичный оператор в банаховом
пространстве
.
Покажем, что если
бесконечномерно, то оператор
не вполне непрерывен. Для этого достаточно
показать, что единичный шар в
(который переводится оператором
в себя) не компактен. Это в свою очередь
вытекает из следующей леммы.
Лемма: Пусть
–
линейно независимые векторы в нормированном
пространстве
и пусть
– подпространство порожденное векторами
.
Тогда существует последовательность
векторов
,
удовлетворяющая следующим условиям:
1)
2)
3)
– расстояние вектора
от
,
т.е.
Пользуясь этой леммой, в единичном
шаре всякого бесконечномерного
нормированного пространства можно
построить последовательность векторов
,
для которой
.
Ясно, что такая последовательность не
может содержать никакой сходящейся
подпоследовательности. А это и означает
отсутствие компактности.
Примеры компактных операторов.
Простейшим примером компактного
оператора является одномерный линейный
оператор вида:
,
где
– фиксированный элемент из пространства
,
а
– фиксированный линейный функционал
из пространства
,
которое является банаховым пространством.
Рассмотрим в пространстве
оператор
,
преобразующий
в себя и задаваемый бесконечной системой
равенств
при условии, что двойной ряд
сходится. Такой оператор линеен и норма
.
Докажем что он компактен. Введем
матричные линейные операторы
в пространстве
,
определяемые матрицами
,
следующим образом:
,
где
при
,
и
при
.
Иными словами, матрица
получается из матрицы
,
если элементы всех строк
,
начиная с
,
заменить нулями. Отсюда вытекает, что,
если
,
то, каков бы ни был элемент
,
будет
при
.
Следовательно, совокупность значений
каждого из операторов
конечномерна, а потому операторы
вполне непрерывны. Представим разность
с помощью матрицы. Из оценки
видно, что
.
Следовательно, оператор
компактен. ([2], стр. 307).
3. В пространстве непрерывных
функций
важный класс компактных операторов
образуют операторы вида:
(3), где функция
непрерывна на квадрате
.
Покажем справедливость следующего
утверждения: если функция
непрерывна на квадрате
,
то формула (3) определяет в пространстве
компактный оператор.
Действительно, в указанных
условиях интеграл (3) существует для
любого
из
,
то есть функция
определена. Пусть
.
На квадрате
функция
равномерно непрерывна по теореме
Кантора, т.к. она непрерывна на замкнутом
и ограниченном множестве в
.
Значит,
.
Оценим разность
:
,
при
.
Полученное равенство показывает,
что функция
непрерывна, то есть формула (3) действительно
определяет оператор, переводящий
пространство
в себя.
Из этого же неравенства видно,
что если
– ограниченное множество в
,
то соответствующее множество
равностепенно непрерывно. Таким образом,
если выполняется неравенство
,
то
,
То есть ограниченное множество
перейдет в равномерно ограниченное.
Таким образом, оператор (3) переводит
всякое ограниченное множество из
в множество функций, равномерно
ограниченное и равностепенно непрерывное,
т.е. предкомпактное по теореме Арцела.
4. Оператор Вольтерра
Рассмотрим оператор
,
где
,
в
.
Для доказательства компактности
оператора Вольтерра покажем, что
множество
,
равностепенно непрерывно и равномерно
ограничено.
Равномерная ограниченность.
Оценим
,
а это значит, что множество равномерно ограниченно.
Равностепенная непрерывность.
По определению, равностепенная непрерывность означает, что
.
Возьмем произвольную функцию
.
Найдем ее образ
.
Тогда
.
Тогда, если положить
,
равностепенная непрерывность показана.
Таким образом, компактность оператора Вольтерра доказана.
Литература
Колмогоров, А.Н. Элементы теорий функций и функционального анализа [Текст] / А.Н. Колмогоров, С.В. Фомин. – М.: Физматлит, 2004.
Вулих, Б.З. Введение в функциональный анализ [Текст] / Б.З. Вулих. –Изд. 2, перераб. и доп. – М., 1967.
Князев, П.Н. Функциональный анализ [Текст] / П.Н. Князев– Изд. 2, перераб. М., 2003.
Люстерник, Л.А. Элементы функционального анализа [Текст] / Л.А. Люстерник В.И. Соболев– М., 1951.