Кольца и полукольца частных
Содержание
Введение
Глава 1.Построение классического полукольца частных
Глава 2.Построение полного полукольца частных
Глава 3.Связь между полным и классическим полукольцами частных
Библиографический список
Введение
В настоящее время теория полуколец активно развивается и находит своё применение в теории автоматов, компьютерной алгебре и других разделах математики.
В работе построены полное и классическое полукольца частных, а так же рассмотрена их связь.
Прежде чем начать рассмотрение этих структур, определим коммутативное полукольцо частных следующим образом.
Непустое множество
 с определёнными на нём бинарными
операциями
с определёнными на нём бинарными
операциями
 и
и
 называется
коммутативным полукольцом, если
выполняется следующие аксиомы:
называется
коммутативным полукольцом, если
выполняется следующие аксиомы:
A1.
 - коммутативная полугруппа с нейтральным
элементом
- коммутативная полугруппа с нейтральным
элементом
 ,
т.е.
,
т.е.
1)

 ;
;
2)


3)



А2.
 - коммутативная полугруппа с нейтральным
элементом 1, т.е.
- коммутативная полугруппа с нейтральным
элементом 1, т.е.
1)

 ;
;
2)


3)



А3. умножение дистрибутивно относительно сложения:

 ,
,
 .
.
А4.

 .
.
Таким образом, можно сказать, что полукольцо отличается от кольца тем, что аддитивная операция в нём необратима.
Глава 1.
Для построения классического полукольца частных можно воспользоваться следующим методом:
Рассмотрим пары неотрицательных
целых чисел
 .
.
Будем считать пары
 и
и
 эквивалентными, если
эквивалентными, если
 ,
получим разбиение множества пар на
классы эквивалентности.
,
получим разбиение множества пар на
классы эквивалентности.
Затем введём операции на классах, превращающие множество классов эквивалентных пар в полуполе, которое содержит полукольцо неотрицательных чисел.
Определение>1>.
Элемент
 назовём мультипликативно сокращаемым,
если для
назовём мультипликативно сокращаемым,
если для
 из
равенства
из
равенства
 следует,
что
следует,
что
 .
.
Обозначим через
 множество всех мультипликативно
сокращаемых элементов.
множество всех мультипликативно
сокращаемых элементов.
Утверждение>1>.Мультипликативно сокращаемый элемент является неделителем нуля.
Пусть
 -
делитель нуля, т.е.
-
делитель нуля, т.е.
 для некоторого
для некоторого
 .
Тогда
.
Тогда
 ,
но
,
но
 не
является мультипликативно сокращаемым.
▲
не
является мультипликативно сокращаемым.
▲
Пусть
 - коммутативное полукольцо с возможностью
сокращения на элементы из
- коммутативное полукольцо с возможностью
сокращения на элементы из
 .
Рассмотрим множество упорядоченных
пар
.
Рассмотрим множество упорядоченных
пар
 .
Введём отношение
на
.
Введём отношение
на
 :
:
 для всех
для всех
 и
и
 .
.
Предложение>1>.
Отношение
является отношением эквивалентности
на
 .
.
Покажем, что является отношением рефлективности, симметричности и транзитивности.
1.Рефлективность: в силу
коммутативности полукольца

 ;
;
2. Симметричность:
 ;
;
3.Транзитивность:
 Таким
образом, отношение
является отношением эквивалентности
на
Таким
образом, отношение
является отношением эквивалентности
на
 .
.
Полукольцо
 разбивается на классы эквивалентности;
в каждом классе находятся те элементы,
которые находятся в отношении .
Обозначим
разбивается на классы эквивалентности;
в каждом классе находятся те элементы,
которые находятся в отношении .
Обозначим
 класс эквивалентности пары
класс эквивалентности пары
 .
Введём операции на множестве
.
Введём операции на множестве
 всех классов эквивалентности:
всех классов эквивалентности:

 т.к. для
т.к. для
 ,
,
 ,
,
 выполнено
выполнено
 отсюда т.к.
отсюда т.к.
 получаем
получаем
 и поскольку
и поскольку
 то
то
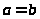 следовательно
следовательно
 .
.
Покажем корректность введённых операций:
Пусть
 ,
,
 ,
тогда
,
тогда

 ▲
▲
Теорема>1>.
 - коммутативное полукольцо с 1.
- коммутативное полукольцо с 1.
 .
.
Доказательство.
Чтобы доказать, что множество
 всех классов эквивалентности является
коммутативным полукольцом с 1, нужно
показать замкнутость на нём операций:
всех классов эквивалентности является
коммутативным полукольцом с 1, нужно
показать замкнутость на нём операций:
сложение: для
 и
и

1.

2.

Так как правые части равны, то левые части тоже равны:

3. покажем, что для

 .
.
Так как

Класс
 является нейтральным по +:
является нейтральным по +:

Из равенства
 тогда
тогда
 .
.
Для

 составляет отдельный класс, играющий
в
составляет отдельный класс, играющий
в
 роль нуля.
роль нуля.
умножение: для
 и
и

1.

2.


Из равенства правых частей
следует, что

3. покажем, что для

 .
.
Пусть

Класс
 является нейтральным по умножению
(единицей полукольца), т.к.
является нейтральным по умножению
(единицей полукольца), т.к.
 ,
поскольку из равенства
,
поскольку из равенства
 тогда
тогда
 .
.
4. умножение дистрибутивно относительно сложения:


Следовательно, правосторонний дистрибутивный закон выполняется:

Аналогично доказывается левосторонний закон дистрибутивности.
Таким образом, доказано, что
 является коммутативным полукольцом с
1.
является коммутативным полукольцом с
1.
Полукольцо
 называется классическим полукольцом
частных полукольца
называется классическим полукольцом
частных полукольца
 .▲
.▲
Глава 2
Для построения полного полукольца
частных можно воспользоваться следующим
методом. Рассмотрим дробь
 как частичный эндоморфизм аддитивной
полугруппы
как частичный эндоморфизм аддитивной
полугруппы
 неотрицательных целых чисел. Его область
определения – идеал
неотрицательных целых чисел. Его область
определения – идеал
 ,
и он переводит
,
и он переводит
 в
в
 ,
где
,
где
 .
Аналогично, дробь
.
Аналогично, дробь
 определена на идеале
определена на идеале
 и переводит
и переводит
 в
в
 .
Эти две дроби эквивалентны, т.е. они
согласованы на пересечении своих
областей определений, равном идеалу
.
Эти две дроби эквивалентны, т.е. они
согласованы на пересечении своих
областей определений, равном идеалу
 ,
поскольку та и другая дробь переводят
,
поскольку та и другая дробь переводят
 в
в
 .
Отношения определяются как классы
эквивалентных дробей. Варьируя этот
метод, можно выбрать в каждом классе
эквивалентности одну «несократимую»
дробь. Рассмотренный выше класс содержит
несократимую дробь
.
Отношения определяются как классы
эквивалентных дробей. Варьируя этот
метод, можно выбрать в каждом классе
эквивалентности одну «несократимую»
дробь. Рассмотренный выше класс содержит
несократимую дробь
 .
.
Данный метод можно применить к произвольному коммутативному полукольцу для построения «полного полукольца частных», где в качестве областей определения допускаются лишь идеалы определённого типа – плотные идеалы.
Определение>2>.>
>Идеал
 коммутативного полукольца
коммутативного полукольца
 называется плотным, если для
называется плотным, если для
 и
и
 выполняется равенство
выполняется равенство
 тогда и только тогда, когда
тогда и только тогда, когда
 .
.
Свойства плотных идеалов
полукольца
 :
:
10
 - плотный идеал.
- плотный идеал.
Доказательство:
Пусть для
 выполнено
выполнено
 .
Положим
.
Положим
 ,
тогда
,
тогда
 .
Таким образом
.
Таким образом
 - плотный идеал по определению. ▲
- плотный идеал по определению. ▲
20
Если
 - плотный идеал и
- плотный идеал и
 ,
то идеал
,
то идеал
 плотный.
плотный.
Доказательство:
Если
 -
плотный идеал, то для
-
плотный идеал, то для
 из равенства
из равенства
 следует
следует
 .
Пусть для
.
Пусть для
 выполнено
выполнено
 .
Так как по условию
.
Так как по условию
 возьмём
возьмём
 .
Тогда т.к.
.
Тогда т.к.
 -
плотный идеал получаем
-
плотный идеал получаем
 отсюда
отсюда
 .
Таким образом
.
Таким образом
 - плотный идеал по определению. ▲
- плотный идеал по определению. ▲
30
Если
 и
и
 - плотные идеалы, то
- плотные идеалы, то
 и
и
 - так же плотные идеалы.
- так же плотные идеалы.
Доказательство:
Положим для
 выполняется
выполняется
 .
Пусть
.
Пусть
 ,
где
,
где
 ,
,
 .
Элемент
.
Элемент
 т.к.
т.к.
 ,
тогда верно равенство
,
тогда верно равенство
 отсюда
отсюда
 ,
т.к.
,
т.к.
 - плотный идеал имеем
- плотный идеал имеем
 ,
,
 ,
и
,
и
 -
плотный,
-
плотный,
 .
Таким образом
.
Таким образом
 - плотный идеал.
- плотный идеал.
Пусть
 ,
,
 тогда
по определению идеала:
тогда
по определению идеала:
 .
С другой стороны
.
С другой стороны
 значит
значит
 .
Тогда по 20
.
Тогда по 20
 - плотный идеал. ▲
- плотный идеал. ▲
40
Если
 ,
то 0 не является плотным идеалом.
,
то 0 не является плотным идеалом.
Доказательство.
Пусть
 .
Для
.
Для
 и
и
 выполнено
выполнено
 отсюда 0 не является плотным идеалом. ▲
отсюда 0 не является плотным идеалом. ▲
Определение>3>.>
> Дробью
назовём элемент
 ,
где
,
где
 - некоторый плотный идеал. (
- некоторый плотный идеал. ( - сокращение
от
- сокращение
от
 - гомоморфизм, в данном случае:
- гомоморфизм, в данном случае:
 -
гомоморфизм
-
гомоморфизм
 )
)
Таким образом,
 - гомоморфизм аддитивных полугрупп, для
которого
- гомоморфизм аддитивных полугрупп, для
которого
 для
для
 и
и
 .
.
Введём так же дроби
 ,
положив
,
положив
 и
и
 для
для
 .
.
Сложение и умножение дробей определяются следующим образом:
пусть
 и
и
 тогда
тогда
 ,
,

 ,
,
 .
.
Покажем, что
 является идеалом, где
является идеалом, где
 т.е. сохраняются операции:
т.е. сохраняются операции:
1. Если
 ,
то
,
то
 .
.
Пусть
 ,
,
 ,
тогда
,
тогда
 .
.
2. Если
 и
и
 ,
то
,
то
 .
По условию
.
По условию
 .
.
Так как
 - коммутативное полукольцо, то
- коммутативное полукольцо, то
 .
.
 .
Таким образом,
.
Таким образом,
 - идеал.
- идеал.
Покажем, что идеал
 является плотным: надо доказать, что
плотный идеал -
является плотным: надо доказать, что
плотный идеал -
 ,
т.е.
,
т.е.
 .
.
По определению сложения и
умножения
 ,
т.е.
,
т.е.
 содержит плотный идеал
содержит плотный идеал
 значит, по свойству 20
идеал
значит, по свойству 20
идеал
 является плотным.
является плотным.
Дроби образуют аддитивную
коммутативную полугруппу
 с нулём и полугруппу
с нулём и полугруппу
 с единицей. То есть образуют полукольцо.
с единицей. То есть образуют полукольцо.
Доказательство:
1. По определению сложения и умножения:
 ,
,
 .
.
 ,
,

2. Коммутативность:

3. Ассоциативность:
 4.
Нейтральный элемент.
4.
Нейтральный элемент.


5. Дистрибутивность:

Правосторонняя дистрибутивность аналогично.
Таким образом, дроби образуют полукольцо.
Определение>4>.
Будем писать
 если
если
 и
и
 согласованы на пересечении своих
областей определений, т.е.
согласованы на пересечении своих
областей определений, т.е.
 для
для
 .
.
Лемма 1.
 тогда и только тогда, когда
тогда и только тогда, когда
 и
и
 согласованы на некотором плотном идеале.
согласованы на некотором плотном идеале.
Доказательство.
Если
 то
то
 и
и
 согласованы на
согласованы на
 .
По свойству 30
идеал
.
По свойству 30
идеал
 является плотным. Следовательно,
является плотным. Следовательно,
 и
и
 согласованы на плотном идеале.
согласованы на плотном идеале.
Обратно, пусть
 и
и
 согласованы на плотном идеале
согласованы на плотном идеале
 .
Тогда если
.
Тогда если
 и
и
 ,
то
,
то
 отсюда в силу плотности идеала
отсюда в силу плотности идеала
 ,
,
 для
для
 ,
но это равенство выполняется тогда,
когда пересечением областей определений
,
но это равенство выполняется тогда,
когда пересечением областей определений
 и
и
 является
является
 отсюда следует, что
отсюда следует, что
 .▲
.▲
Лемма 2.
Отношение
 является конгруэнцией на системе
является конгруэнцией на системе
 .
.
Доказательство.
Для того чтобы доказать, что
 - конгруэнция, нужно показать:
- конгруэнция, нужно показать:
1. отношение
 - рефлексивно, симметрично, транзитивно.
- рефлексивно, симметрично, транзитивно.
Рефлективность:
 и
и
 согласованы на плотном идеале
согласованы на плотном идеале
 .
.
Симметричность: пусть
 ,
т.е.
,
т.е.
 и
и
 согласованы на
согласованы на
 .
.
Транзитивность: пусть
 и
и
 ,
т.е.
,
т.е.
 и
и
 согласованы на плотном идеале
согласованы на плотном идеале

 и
и
 согласованы на плотном идеале
согласованы на плотном идеале
 .
Значит
.
Значит
 и
и
 согласованы на идеале
согласованы на идеале
 ,
являющемся плотным , и
,
являющемся плотным , и
 согласована с
согласована с
 на
на
 ,
тогда
,
тогда


 согласована с
согласована с
 на плотном идеале
на плотном идеале
 по Лемме 1
по Лемме 1

Таким образом,
 - отношение эквивалентности.
- отношение эквивалентности.
2. отношение
 сохраняет полукольцевые операции.
сохраняет полукольцевые операции.
Пусть
 и
и
 ,
т.е.
,
т.е.
 для
для
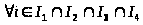 и
и
 для
для
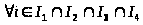 .
.
Тогда


 и
и
 определены и согласованы на плотном
идеале
определены и согласованы на плотном
идеале
 отсюда по Лемме 1
отсюда по Лемме 1
 .
.
Пусть
 и
и
 ,
т.е.
,
т.е.
 для
для
 и
и
 для
для
 .
.
Тогда


 и
и
 определены и согласованы на плотном
идеале
определены и согласованы на плотном
идеале
 отсюда по Лемме 1
отсюда по Лемме 1
 .▲
.▲
Теорема>2>.Если
 - коммутативное полукольцо то система
- коммутативное полукольцо то система
 так же является коммутативным полукольцом.
так же является коммутативным полукольцом.
 .
(Будем называть
.
(Будем называть
 полным полукольцом частных полукольца
полным полукольцом частных полукольца
 )
)
Доказательство.
 - разбивает множество дробей
- разбивает множество дробей
 на
на
 непересекающихся классов эквивалентности.
непересекающихся классов эквивалентности.
По Лемме 2
все тождества выполняющиеся в
 справедливы и в
справедливы и в
 .
.
Чтобы убедится, что
 коммутативное полукольцо остаётся
проверить справедливость законов
дистрибутивности и коммутативности.
коммутативное полукольцо остаётся
проверить справедливость законов
дистрибутивности и коммутативности.
1. Дистрибутивность.
Отображения:
 и
и
 согласованы на идеале
согласованы на идеале
 покажем, что образы отображений
покажем, что образы отображений
 и
и
 совпадают на этом идеале:
совпадают на этом идеале:
пусть
 ,
где
,
где
 .
.
Тогда
 .
.
Областью определения
 является
является
 .
По определению идеала:
.
По определению идеала:
 то
то
 для
для
 ,
а идеал
,
а идеал
 (свойство 30)
то:
(свойство 30)
то:
 .
Тогда по определению сложения
.
Тогда по определению сложения
 отсюда следует
отсюда следует
 .
Покажем
.
Покажем
 .
По определению
.
По определению

Аналогично
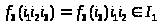 .
.
Тогда:
 Таким
образом,
Таким
образом,
 где
где
 .
По свойству 30
.
По свойству 30
 -
плотный идеал значит
-
плотный идеал значит
 и
и
 согласованы на плотном идеале
согласованы на плотном идеале


 .
.
2. Коммутативность.
Отображения
 и
и
 согласованы на плотном идеале
согласованы на плотном идеале
 докажем что их образы совпадают на этом
идеале:
докажем что их образы совпадают на этом
идеале:
 .
.
Доказано ранее, что
 пусть элементы
пусть элементы
 тогда
тогда

Отсюда следует, что
 и
и
 согласованы на плотном идеале
согласованы на плотном идеале
 .
.
Таким образом,
 по Лемме 1.
по Лемме 1.
Наконец
 сопоставим дробь:
сопоставим дробь:
 с областью определения
с областью определения
 при которой
при которой
 переходит в
переходит в
 .
.
Предложение>2>.
Отображение
 является гомоморфизмом т.е. сохраняет
операции:
является гомоморфизмом т.е. сохраняет
операции:


Доказательство:
1. Пусть
 ,
,
 и
и
 где
где
 и
и
 .
.
Нужно показать, что
 .
Покажем равенство образов
.
Покажем равенство образов
 и
и
 .
.
Рассмотрим дробь
 ,
такую что
,
такую что
 для
для
 . (1)
. (1)
С другой стороны рассмотрим
дроби
 и
и

 ,
такие что
,
такие что
 для
для
 . (2)
. (2)
Из (1) и (2) следует, что
 .
.
По свойству сложения смежных классов:
 для
для

2. Пусть
 ,
,
 и
и
 где
где
 и
и
 .
.
Нужно показать, что
 .
Покажем равенство образов
.
Покажем равенство образов
 и
и
 .
.
Рассмотрим дробь
 ,
такую что
,
такую что
 для
для
 . (3)
. (3)
С другой стороны рассмотрим
дроби
 и
и

 ,
такие что
,
такие что
 для
для
 . (4)
. (4)
Из (3) и (4) следует, что
 .
.
По свойству умножения смежных классов:
 для
для
 .
.
Таким образом
 гомоморфизм.
гомоморфизм.
Пусть
 ,
тогда
,
тогда
 т.е.
т.е.
 и
и
 согласованы на некотором плотном идеале
согласованы на некотором плотном идеале
 значит
значит
 для
для
 ,
так как
,
так как
 -
плотный идеал, то
-
плотный идеал, то
 отсюда
отсюда
 - инъективно.
- инъективно.
Поэтому, гомоморфизм
 является мономорфизмом и
является мономорфизмом и
 вкладывается в полное полукольцо
частных.
вкладывается в полное полукольцо
частных.
Гомоморфизм
 будем называть каноническим мономорфизмом
будем называть каноническим мономорфизмом
 в
в
 .▲
.▲
Глава 3.
Определение>5>.Любому
мультипликативно сокращаемому элементу
 сопоставим плотный идеал
сопоставим плотный идеал
 .
Если
.
Если
 ,
то элемент
,
то элемент
 назовём классической дробью, полагая
назовём классической дробью, полагая
 для
для
 .
.
Теорема>3>.
Множество дробей
 образует подполукольцо полного полукольца
частных, изоморфное классическому
полукольцу частных
образует подполукольцо полного полукольца
частных, изоморфное классическому
полукольцу частных
 полукольца
полукольца
 .
.
Доказательство:
Рассмотрим отображение
 ,
т.е.
,
т.е.
 .
.
1. Докажем, что
 - отображение: если
- отображение: если
 и
и
 ,
,
 ,
где
,
где
 ,
,
 ,
то
,
то
 .
.
Имеем

Возьмём элемент
 из пересечения плотных идеалов
из пересечения плотных идеалов
 ,
т.е.
,
т.е.
 и
и

Тогда
 ,
домножим
,
домножим
 на
на
 получим
получим
 .
Так как
.
Так как
 и на
и на
 выполняется коммутативность по умножению,
то
выполняется коммутативность по умножению,
то
 ,
,
 отсюда
отсюда
 для
для

 .
.
2. Докажем, что
 является полукольцевым гомоморфизмом,
т.е. сохраняются полукольцевые операции.
является полукольцевым гомоморфизмом,
т.е. сохраняются полукольцевые операции.
2.1


 .
Покажем, что дробь
.
Покажем, что дробь
 согласована с
согласована с
 на плотном идеале
на плотном идеале
 .
.
Пусть
 ,
,
 .
.

для
 .
.
Следовательно
 .
.
2.2

 .
.
Идеал
 содержит
содержит
 ,
покажем, что
,
покажем, что
 и
и
 согласованы на плотном идеале
согласованы на плотном идеале
 .
.
Пусть
 ,
,
 .
Тогда
.
Тогда
 для
для
 .
.
Значит
 .
.
Таким образом
 - полукольцевой гомоморфизм классического
полукольца частных
- полукольцевой гомоморфизм классического
полукольца частных
 в полное полукольцо частных
в полное полукольцо частных
 .
.
3. Докажем, что
 - инъективный гомоморфизм.
- инъективный гомоморфизм.
Пусть для
 .
Предположим, что дроби
.
Предположим, что дроби
 и
и
 согласованы на некотором плотном идеале
согласованы на некотором плотном идеале
 ,
т.е. для
,
т.е. для
 выполнено
выполнено
 .
Но
.
Но
 ,
,
 .
Тогда
.
Тогда
 .
Домножим обе части равенства на
.
Домножим обе части равенства на
 получим:
получим:
 т.к.
т.к.
 -
плотный идеал
-
плотный идеал
 ,
что противоречит условию.
,
что противоречит условию.
Значит,
 является инъективным гомоморфизмом
или мономорфизмом
является инъективным гомоморфизмом
или мономорфизмом
 в
в
 .
.
Так как
 ,
то
,
то
 ,
где
,
где
 - элемент подполукольца полного полукольца
частных
- элемент подполукольца полного полукольца
частных
 ,
т.е.
,
т.е.
 и
и
 .
Поскольку
.
Поскольку
 - инъективный гомоморфизм, то по теореме
о гомоморфизме существует изоморфизм
- инъективный гомоморфизм, то по теореме
о гомоморфизме существует изоморфизм
 отсюда следует
отсюда следует
 .
.
Мономорфизм
 называется вложением классического
полукольца частных
называется вложением классического
полукольца частных
 в полное полукольцо частных
в полное полукольцо частных
 полукольца
полукольца
 .▲
.▲
Библиографический список
Вечтомов, Е. М. Введение в полукольца [Текст] / Е. М. Вечтомов. – Киров.: ВГПУ, 2000.
Ламбек, И. Кольца и модули [Текст] / И. Ламбек. – Москва.: Мир, 1971. – 288 с.
Чермных, В. В. Полукольца [Текст] / В. В. Чермных. – Киров.: ВГПУ, 1997. – 131 с.