Классы конечных групп F, замкнутые о взаимно простых индексов относительно произведения обобщенно субнормальных F-подгрупп
Министерство образования Республики Беларусь
Учреждение образования
"Гомельский государственный университет им. Ф. Скорины"
Математический факультет
Кафедра алгебры и геометрии
КЛАССЫ
КОНЕЧНЫХ ГРУПП >
 >,
ЗАМКНУТЫЕ О ВЗАИМНО ПРОСТЫХ ИНДЕКСОВ
ОТНОСИТЕЛЬНО ПРОИЗВЕДЕНИЯ ОБОБЩЕННО
СУБНОРМАЛЬНЫХ >
>,
ЗАМКНУТЫЕ О ВЗАИМНО ПРОСТЫХ ИНДЕКСОВ
ОТНОСИТЕЛЬНО ПРОИЗВЕДЕНИЯ ОБОБЩЕННО
СУБНОРМАЛЬНЫХ >
 >-ПОДГРУПП
>-ПОДГРУПП
Курсовая работа
Исполнитель:
Студентка группы М-53 МОКЕЕВА О. А.
Научный руководитель:
доктор ф-м наук, профессор Семенчук В.Н.
Гомель 2009
Оглавление
ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ
Введение
1 Некоторые базисные леммы
2 Критерий принадлежности групп, факторизуемых >обобщенно субнормальными 010009000003a400000002001c0000000000030000001e000500000009020000000005000000020101000000050000000102ffffff00050000002e0118000000050000000c02a001a001050000000b02000000001200000026060f001a00ffffffff000010000000c0ffffffc6ffffff60010000660100000b00000026060f000c004d61746854797065000020001c000000fb0280fe0000000000009001010000cc0402001054696d6573204e657720526f6d616e00b8aef377c1aef3772040f577bf416648040000002d01000008000000320a600146000100000046010a00000026060f000a00ffffffff0100000000001c000000fb021000070000000000bc02000000cc0102022253797374656d0000012c0a0948e31100b8aef377c1aef3772040f577bf416648040000002d01010004000000f0010000040000002701ffff030000000000-подгруппами, индексы которых> взаимно просты, наследственно насыщенным формациям
Заключение
Список использованных источников
Перечень условных обозначений
Рассматриваются только конечные группы. Вся терминология заимствована из [44, 47].
>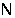 >
--- множество
всех натуральных чисел;
>
--- множество
всех натуральных чисел;
> >
--- множество
всех простых чисел;
>
--- множество
всех простых чисел;
> >
--- некоторое
множество простых чисел, т. е. >
>
--- некоторое
множество простых чисел, т. е. >
 >;
>;
> >
>
--- дополнение
к >
 >
во множестве всех простых чисел; в
частности, >
>
во множестве всех простых чисел; в
частности, >
 >;
>;
примарное
число --- любое число вида >
 >.
>.
Буквами >
 >
обозначаются простые числа.
>
обозначаются простые числа.
Пусть >
 >
--- группа. Тогда:
>
--- группа. Тогда:
> >
--- порядок
группы >
>
--- порядок
группы >
 >;
>;
> >
>
--- множество
всех простых делителей порядка группы
>
 >;
>;
> >-группа
--- группа >
>-группа
--- группа >
 >,
для которой >
>,
для которой >
 >;
>;
> >-группа
--- группа >
>-группа
--- группа >
 >,
для которой >
>,
для которой >
 >;
>;
> >
--- коммутант
группы >
>
--- коммутант
группы >
 >,
т. е. подгруппа, порожденная коммутаторами
всех элементов группы >
>,
т. е. подгруппа, порожденная коммутаторами
всех элементов группы >
 >;
>;
> >
--- подгруппа
Фиттинга группы >
>
--- подгруппа
Фиттинга группы >
 >,
т. е. произведение всех нормальных
нильпотентных подгрупп группы >
>,
т. е. произведение всех нормальных
нильпотентных подгрупп группы >
 >;
>;
> >
--- наибольшая
нормальная >
>
--- наибольшая
нормальная >
 >-нильпотентная
подгруппа группы >
>-нильпотентная
подгруппа группы >
 >;
>;
> >
--- подгруппа
Фраттини группы >
>
--- подгруппа
Фраттини группы >
 >,
т. е. пересечение всех максимальных
подгрупп группы >
>,
т. е. пересечение всех максимальных
подгрупп группы >
 >;
>;
> >
--- наибольшая
нормальная >
>
--- наибольшая
нормальная >
 >-подгруппа
группы >
>-подгруппа
группы >
 >;
>;
> >
--- >
>
--- >
 >-холлова
подгруппа группы >
>-холлова
подгруппа группы >
 >;
>;
> >
--- силовская
>
>
--- силовская
>
 >-подгруппа
группы >
>-подгруппа
группы >
 >;
>;
> >
--- дополнение
к силовской >
>
--- дополнение
к силовской >
 >-подгруппе
в группе >
>-подгруппе
в группе >
 >,
т. е. >
>,
т. е. >
 >-холлова
подгруппа группы >
>-холлова
подгруппа группы >
 >;
>;
> >
--- нильпотентная
длина группы >
>
--- нильпотентная
длина группы >
 >;
>;
> >
--- >
>
--- >
 >-длина
группы >
>-длина
группы >
 >;
>;
> >
--- минимальное
число порождающих элементов группы >
>
--- минимальное
число порождающих элементов группы >
 >;
>;
> >
--- цоколь
группы >
>
--- цоколь
группы >
 >,
т. е. подгруппа, порожденная всеми
минимальными нормальными подгруппами
группы >
>,
т. е. подгруппа, порожденная всеми
минимальными нормальными подгруппами
группы >
 >;
>;
> >
--- циклическая
группа порядка >
>
--- циклическая
группа порядка >
 >.
>.
Если >
 >
и >
>
и >
 >
--- подгруппы группы >
>
--- подгруппы группы >
 >,
то :
>,
то :
> >
--- >
>
--- >
 >
является подгруппой группы >
>
является подгруппой группы >
 >;
>;
> >
--- >
>
--- >
 >
является собственной подгруппой группы
>
>
является собственной подгруппой группы
>
 >;
>;
> >
--- >
>
--- >
 >
является нормальной подгруппой группы
>
>
является нормальной подгруппой группы
>
 >;
>;
> >
>
--- ядро
подгруппы >
 >
в группе >
>
в группе >
 >,
т. е. пересечение всех подгрупп, сопряженных
с >
>,
т. е. пересечение всех подгрупп, сопряженных
с >
 >
в >
>
в >
 >;
>;
> >
--- нормальное
замыкание подгруппы >
>
--- нормальное
замыкание подгруппы >
 >
в группе >
>
в группе >
 >,
т. е. подгруппа, порожденная всеми
сопряженными с >
>,
т. е. подгруппа, порожденная всеми
сопряженными с >
 >
подгруппами группы >
>
подгруппами группы >
 >;
>;
> >
--- индекс
подгруппы >
>
--- индекс
подгруппы >
 >
в группе >
>
в группе >
 >;
>;
> >;
>;
> >
--- нормализатор
подгруппы >
>
--- нормализатор
подгруппы >
 >
в группе >
>
в группе >
 >;
>;
> >
--- централизатор
подгруппы >
>
--- централизатор
подгруппы >
 >
в группе >
>
в группе >
 >;
>;
>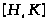 >
--- взаимный
коммутант подгрупп >
>
--- взаимный
коммутант подгрупп >
 >
и >
>
и >
 >;
>;
> >
--- подгруппа,
порожденная подгруппами >
>
--- подгруппа,
порожденная подгруппами >
 >
и >
>
и >
 >.
>.
Минимальная
нормальная подгруппа группы >
 >
--- неединичная нормальная подгруппа
группы >
>
--- неединичная нормальная подгруппа
группы >
 >,
не содержащая собственных неединичных
нормальных подгрупп группы >
>,
не содержащая собственных неединичных
нормальных подгрупп группы >
 >;
>;
> >
--- >
>
--- >
 >
является максимальной подгруппой группы
>
>
является максимальной подгруппой группы
>
 >.
>.
Если >
 >
и >
>
и >
 >
--- подгруппы группы >
>
--- подгруппы группы >
 >,
то:
>,
то:
> >
--- прямое
произведение подгрупп >
>
--- прямое
произведение подгрупп >
 >
и >
>
и >
 >;
>;
> >
--- полупрямое
произведение нормальной подгруппы >
>
--- полупрямое
произведение нормальной подгруппы >
 >
и подгруппы >
>
и подгруппы >
 >;
>;
> >
--- >
>
--- >
 >
и >
>
и >
 >
изоморфны;
>
изоморфны;
> >
--- регулярное
сплетение подгрупп >
>
--- регулярное
сплетение подгрупп >
 >
и >
>
и >
 >.
>.
Подгруппы >
 >
и >
>
и >
 >
группы >
>
группы >
 >
называются перестановочными, если >
>
называются перестановочными, если >
 >.
>.
Группу >
 >
называют:
>
называют:
> >-замкнутой,
если силовская >
>-замкнутой,
если силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >
нормальна в >
>
нормальна в >
 >;
>;
> >-нильпотентной,
если >
>-нильпотентной,
если >
 >-холлова
подгруппа группы >
>-холлова
подгруппа группы >
 >
нормальна в >
>
нормальна в >
 >;
>;
> >-разрешимой,
если существует нормальный ряд, факторы
которого либо >
>-разрешимой,
если существует нормальный ряд, факторы
которого либо >
 >-группы,
либо >
>-группы,
либо >
 >-группы;
>-группы;
> >-сверхразрешимой,
если каждый ее главный фактор является
либо >
>-сверхразрешимой,
если каждый ее главный фактор является
либо >
 >-группой,
либо циклической группой;
>-группой,
либо циклической группой;
нильпотентной, если все ее силовские подгруппы нормальны;
разрешимой,
если существует номер >
 >
такой, что >
>
такой, что >
 >;
>;
сверхразрешимой, если она обладает главным рядом, все индексы которого являются простыми числами.
Монолитическая группа --- неединичная группа, имеющая единственную минимальную нормальную подгруппу.
> >-замкнутая
группа --- группа, обладающая нормальной
холловской >
>-замкнутая
группа --- группа, обладающая нормальной
холловской >
 >-подгруппой.
>-подгруппой.
> >-специальная
группа --- группа, обладающая нильпотентной
нормальной холловской >
>-специальная
группа --- группа, обладающая нильпотентной
нормальной холловской >
 >-подгруппой.
>-подгруппой.
> >-разложимая
группа --- группа, являющаяся одновременно
>
>-разложимая
группа --- группа, являющаяся одновременно
>
 >-специальной
и >
>-специальной
и >
 >-замкнутой.
>-замкнутой.
Группа Шмидта --- это конечная ненильпотентная группа, все собственные группы которой нильпотентны.
Добавлением
к подгруппе >
 >
группы >
>
группы >
 >
называется такая подгруппа >
>
называется такая подгруппа >
 >
из >
>
из >
 >,
что >
>,
что >
 >.
>.
Цепь --- это совокупность вложенных друг в друга подгрупп.
Ряд подгрупп --- это цепь, состоящая из конечного числа членов и проходящая через единицу.
Ряд подгрупп
>
 >
называется:
>
называется:
субнормальным,
если >
 >
для любого >
>
для любого >
 >;
>;
нормальным,
если >
 >
для любого >
>
для любого >
 >;
>;
главным, если
>
 >
является минимальной нормальной
подгруппой в >
>
является минимальной нормальной
подгруппой в >
 >
для всех >
>
для всех >
 >.
>.
Класс групп
--- совокупность групп, содержащая с
каждой своей группой >
 >
и все ей изоморфные группы.
>
и все ей изоморфные группы.
> >-группа
--- группа, принадлежащая классу групп
>
>-группа
--- группа, принадлежащая классу групп
>
 >.
>.
Формация --- класс групп, замкнутый относительно факторгрупп и подпрямых произведений.
Если >
 >
--- класс групп, то:
>
--- класс групп, то:
> >
--- множество
всех простых делителей порядков всех
групп из >
>
--- множество
всех простых делителей порядков всех
групп из >
 >;
>;
> >
--- множество
всех тех простых чисел >
>
--- множество
всех тех простых чисел >
 >,
для которых >
>,
для которых >
 >;
>;
> >
--- формация,
порожденная классом >
>
--- формация,
порожденная классом >
 >;
>;
> >
--- насыщенная
формация, порожденная классом >
>
--- насыщенная
формация, порожденная классом >
 >;
>;
> >
--- класс всех
групп >
>
--- класс всех
групп >
 >,
представимых в виде
>,
представимых в виде
> >
>
где >
 >,
>
>,
>
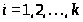 >;
>;
> >;
>;
> >
--- класс всех
минимальных не >
>
--- класс всех
минимальных не >
 >-групп,
т. е. групп не принадлежащих >
>-групп,
т. е. групп не принадлежащих >
 >,
но все собственные подгруппы которых
принадлежат >
>,
но все собственные подгруппы которых
принадлежат >
 >;
>;
> >
--- класс всех
>
>
--- класс всех
>
 >-групп
из >
>-групп
из >
 >;
>;
> >
--- класс всех
конечных групп;
>
--- класс всех
конечных групп;
> >
--- класс всех
разрешимых конечных групп;
>
--- класс всех
разрешимых конечных групп;
> >
--- класс всех
>
>
--- класс всех
>
 >-групп;
>-групп;
>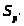 >
--- класс всех
разрешимых >
>
--- класс всех
разрешимых >
 >-групп;
>-групп;
> >
--- класс всех
разрешимых >
>
--- класс всех
разрешимых >
 >-групп;
>-групп;
> >
--- класс всех
нильпотентных групп;
>
--- класс всех
нильпотентных групп;
> >
--- класс всех
разрешимых групп с нильпотентной длиной
>
>
--- класс всех
разрешимых групп с нильпотентной длиной
>
 >.
>.
Если >
 >
и >
>
и >
 >
--- классы групп, то:
>
--- классы групп, то:
> >.
>.
Если >
 >
--- класс групп и >
>
--- класс групп и >
 >
--- группа, то:
>
--- группа, то:
>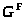 >
--- пересечение
всех нормальных подгрупп >
>
--- пересечение
всех нормальных подгрупп >
 >
из >
>
из >
 >
таких, что >
>
таких, что >
 >;
>;
> >
--- произведение
всех нормальных >
>
--- произведение
всех нормальных >
 >-подгрупп
группы >
>-подгрупп
группы >
 >.
>.
Если >
 >
и >
>
и >
 >
--- формации, то:
>
--- формации, то:
> >
--- произведение
формаций;
>
--- произведение
формаций;
> >
--- пересечение
всех >
>
--- пересечение
всех >
 >-абнормальных
максимальных подгрупп группы >
>-абнормальных
максимальных подгрупп группы >
 >.
>.
Если >
 >
--- насыщенная формация, то:
>
--- насыщенная формация, то:
> >
--- существенная
характеристика формации >
>
--- существенная
характеристика формации >
 >.
>.
> >-абнормальной
называется максимальная подгруппа >
>-абнормальной
называется максимальная подгруппа >
 >
группы >
>
группы >
 >,
если
>,
если
> >,
где >
>,
где >
 >
>
--- некоторая непустая формация.
> >-гиперцентральной
подгруппой в >
>-гиперцентральной
подгруппой в >
 >
называется разрешимая нормальная
подгруппа >
>
называется разрешимая нормальная
подгруппа >
 >
группы >
>
группы >
 >,
если >
>,
если >
 >
обладает субнормальным рядом >
>
обладает субнормальным рядом >
 >
таким, что
>
таким, что
(1) каждый
фактор >
 >
является главным фактором группы >
>
является главным фактором группы >
 >;
>;
(2) если порядок
фактора >
 >
есть степень простого числа >
>
есть степень простого числа >
 >,
то >
>,
то >
 >.
>.
> >
--- >
>
--- >
 >-гиперцентр
группы >
>-гиперцентр
группы >
 >,
т. е. произведение всех >
>,
т. е. произведение всех >
 >-гиперцентральных
подгрупп группы >
>-гиперцентральных
подгрупп группы >
 >.
>.
Введение
Известно, что формация всех сверхразрешимых групп не замкнута относительно произведения нормальных сверхразрешимых подгрупп, но замкнута относительно произведения нормальных сверхразрешимых подгрупп взаимно простых индексов. В связи с этим можно сформулировать следующую проблему.
Проблема.
Классифицировать наследственные
насыщенные формации >
 >
с тем свойством, что любая группа >
>
с тем свойством, что любая группа >
 >,
где >
>,
где >
 >
и >
>
и >
 >
--- >
>
--- >
 >-субнормальные
>
>-субнормальные
>
 >-подгруппы
взаимно простых индексов, принадлежит
>
>-подгруппы
взаимно простых индексов, принадлежит
>
 >.
>.
Именно изучению таких формаций посвящена данная работа. В частности, в классе конечных разрешимых групп получено полное решение данной проблемы.
1 Некоторые базисные леммы
В данном разделе доказаны леммы, которые существенным образом используются при доказательстве основного раздела данной главы.
1.1 Лемма
[18-A]. Пусть >
 >
--- насыщенная формация, >
>
--- насыщенная формация, >
 >
принадлежит >
>
принадлежит >
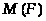 >
и имеет нормальную силовскую >
>
и имеет нормальную силовскую >
 >-подгруппу
>
>-подгруппу
>
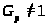 >
для некоторого простого числа >
>
для некоторого простого числа >
 >.
Тогда справедливы следующие утверждения:
>.
Тогда справедливы следующие утверждения:
1) >
 >;
>;
2) >
 >,
где >
>,
где >
 >
--- любое дополнение к >
>
--- любое дополнение к >
 >
в >
>
в >
 >.
>.
Доказательство.
Так как >
 >,
то >
>,
то >
 >,
а значит, >
>,
а значит, >
 >.
Так как >
>.
Так как >
 >
и формация >
>
и формация >
 >
насыщенная, то >
>
насыщенная, то >
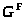 >
не содержится в >
>
не содержится в >
 >.
Так как >
>.
Так как >
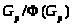 >
--- элементарная группа, то по теореме
2.2.16, >
>
--- элементарная группа, то по теореме
2.2.16, >
 >
обладает >
>
обладает >
 >-допустимым
дополнением >
>-допустимым
дополнением >
 >
в >
>
в >
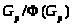 >.
Тогда >
>.
Тогда >
 >,
>
>,
>
 >.
Если >
>.
Если >
 >,
то >
>,
то >
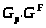 >
отлична от >
>
отлична от >
 >
и, значит, принадлежит >
>
и, значит, принадлежит >
 >.
Но тогда, ввиду равенства >
>.
Но тогда, ввиду равенства >
 >,
имеем
>,
имеем
> >
>
отсюда следует
>
 >
и >
>
и >
 >.
Тем самым доказано, что >
>.
Тем самым доказано, что >
 >.
>.
Докажем
утверждение 2). Очевидно, что >
 >
является >
>
является >
 >-корадикалом
и единственной минимальной нормальной
подгруппой группы >
>-корадикалом
и единственной минимальной нормальной
подгруппой группы >
 >,
причем >
>,
причем >
 >.
Поэтому, ввиду теоремы 2.2.17,
>.
Поэтому, ввиду теоремы 2.2.17,
> >
>
Очевидно,
> >.
Если >
>.
Если >
 >,
то
>,
то
> >
>
отсюда >
 >.
Значит, >
>.
Значит, >
 >.
Лемма доказана.
>.
Лемма доказана.
Пусть >
 >
и >
>
и >
 >
--- произвольные классы групп. Следуя
[55], обозначим через >
>
--- произвольные классы групп. Следуя
[55], обозначим через >
 >
--- множество всех групп, у которых все
>
>
--- множество всех групп, у которых все
>
 >-подгруппы
принадлежат >
>-подгруппы
принадлежат >
 >.
>.
Если >
 >
--- локальный экран, то через >
>
--- локальный экран, то через >
 >
обозначим локальную функцию, обладающую
равенством >
>
обозначим локальную функцию, обладающую
равенством >
 >
для любого простого числа >
>
для любого простого числа >
 >.
>.
1.2 Лемма
[18-A]. Пусть >
 >
и >
>
и >
 >
--- некоторые классы групп. Тогда
справедливы следующие утверждения:
>
--- некоторые классы групп. Тогда
справедливы следующие утверждения:
1) >
 >
--- наследственный класс;
>
--- наследственный класс;
2) >
 >;
>;
3) если >
 >,
то >
>,
то >
 >;
>;
4) если >
 >,
то >
>,
то >
 >
--- класс всех групп;
>
--- класс всех групп;
5) если >
 >
--- формация, а >
>
--- формация, а >
 >
--- насыщенный гомоморф, то >
>
--- насыщенный гомоморф, то >
 >
--- формация;
>
--- формация;
6) если >
 >,
>
>,
>
 >,
>
>,
>
 >
--- некоторые классы групп и >
>
--- некоторые классы групп и >
 >
--- наследственный класс, то >
>
--- наследственный класс, то >
 >
в том и только в том случае, когда >
>
в том и только в том случае, когда >
 >;
>;
7) если >
 >
и >
>
и >
 >
--- гомоморфы и >
>
--- гомоморфы и >
 >,
то >
>,
то >
 >.
>.
Доказательство.
Доказательство утверждений 1), 2), 3) и 4)
следует непосредственно из определения
класса групп >
 >.
>.
Пусть >
 >,
>
>,
>
 >
--- нормальная подгруппа группы >
>
--- нормальная подгруппа группы >
 >
и >
>
и >
 >
--- >
>
--- >
 >-подгруппа
из >
>-подгруппа
из >
 >.
Пусть >
>.
Пусть >
 >
--- добавление к >
>
--- добавление к >
 >
в >
>
в >
 >.
Покажем, что >
>.
Покажем, что >
 >.
Предположим противное. Пусть >
>.
Предположим противное. Пусть >
 >
не входит в >
>
не входит в >
 >.
Тогда >
>.
Тогда >
 >
обладает максимальной подгруппой >
>
обладает максимальной подгруппой >
 >,
не содержащей >
>,
не содержащей >
 >.
Поэтому >
>.
Поэтому >
 >,
а значит, >
>,
а значит, >
 >,
что противоречит определению добавления.
>,
что противоречит определению добавления.
Так как >
 >
--- насыщенный гомоморф, то >
>
--- насыщенный гомоморф, то >
 >.
Но тогда >
>.
Но тогда >
 >
и >
>
и >
 >.
Значит, класс >
>.
Значит, класс >
 >
замкнут относительно гомоморфных
образов.
>
замкнут относительно гомоморфных
образов.
Пусть >
 >.
Пусть >
>.
Пусть >
 >
--- >
>
--- >
 >-подгруппа
из >
>-подгруппа
из >
 >.
Тогда >
>.
Тогда >
 >,
а значит ввиду определения класса >
>,
а значит ввиду определения класса >
 >,
имеем
>,
имеем
> >
>
Так как >
 >
--- формация и >
>
--- формация и >
 >,
то отсюда получаем, что >
>,
то отсюда получаем, что >
 >.
Таким образом, >
>.
Таким образом, >
 >.
>.
Докажем
утверждение 6). Пусть >
 >,
>
>,
>
 >.
Если >
>.
Если >
 >
не входит в >
>
не входит в >
 >,
то получается, что каждая >
>,
то получается, что каждая >
 >-подгруппа
из >
>-подгруппа
из >
 >
принадлежит >
>
принадлежит >
 >,
а значит, >
>,
а значит, >
 >.
Получили противоречие. Поэтому >
>.
Получили противоречие. Поэтому >
 >.
>.
Покажем, что
>
 >.
Предположим, что множество >
>.
Предположим, что множество >
 >
непусто, и выберем в нем группу >
>
непусто, и выберем в нем группу >
 >
наименьшего порядка. Тогда >
>
наименьшего порядка. Тогда >
 >
не входит в >
>
не входит в >
 >.
Пусть >
>.
Пусть >
 >
--- собственная подгруппа из >
>
--- собственная подгруппа из >
 >.
Так как классы >
>.
Так как классы >
 >
и >
>
и >
 >
--- наследственные классы, то >
>
--- наследственные классы, то >
 >.
Ввиду минимальности >
>.
Ввиду минимальности >
 >
имеем >
>
имеем >
 >.
Значит, >
>.
Значит, >
 >.
Получили противоречие. Поэтому >
>.
Получили противоречие. Поэтому >
 >.
>.
Докажем
утверждение 7). Пусть >
 >
и >
>
и >
 >
--- >
>
--- >
 >-подгруппа
из группы >
>-подгруппа
из группы >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >,
>
>,
>
 >.
А это значит, что >
>.
А это значит, что >
 >.
Отсюда нетрудно заметить, что >
>.
Отсюда нетрудно заметить, что >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Итак, >
>.
Итак, >
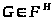 >.
Лемма доказана.
>.
Лемма доказана.
1.3 Лемма
[18-A]. Пусть >
 >
--- наследственная насыщенная формация,
>
>
--- наследственная насыщенная формация,
>
 >
--- ее максимальный внутренний локальный
экран. Тогда и только тогда >
>
--- ее максимальный внутренний локальный
экран. Тогда и только тогда >
 >-корадикал
любой минимальной не >
>-корадикал
любой минимальной не >
 >-группы
является силовской подгруппой, когда:
>-группы
является силовской подгруппой, когда:
1) >
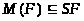 >;
>;
2) формация
>
 >
имеет полный локальный экран >
>
имеет полный локальный экран >
 >
такой >
>
такой >
 >,
что >
>,
что >
 >
для любого >
>
для любого >
 >
из >
>
из >
 >.
>.
Доказательство.
Необходимость. Пусть >
 >
--- максимальный внутренний локальный
экран формации >
>
--- максимальный внутренний локальный
экран формации >
 >.
Пусть >
>.
Пусть >
 >
--- произвольное простое число из >
>
--- произвольное простое число из >
 >.
Так как >
>.
Так как >
 >
--- насыщенный гомоморф, то по лемме
4.1.2, >
>
--- насыщенный гомоморф, то по лемме
4.1.2, >
 >
--- формация.
>
--- формация.
Пусть >
 >
--- формация, имеющая локальный экран >
>
--- формация, имеющая локальный экран >
 >
такой, что >
>
такой, что >
 >
для любого >
>
для любого >
 >
из >
>
из >
 >.
Покажем , что >
>.
Покажем , что >
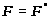 >.
Согласно теореме 2.2.13, >
>.
Согласно теореме 2.2.13, >
 >
--- наследственная формация для любого
>
>
--- наследственная формация для любого
>
 >
из >
>
из >
 >.
Отсюда нетрудно заметить, что >
>.
Отсюда нетрудно заметить, что >
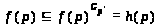 >
для любого >
>
для любого >
 >
из >
>
из >
 >.
А это значит, что >
>.
А это значит, что >
 >.
>.
Пусть >
 >
--- группа минимального порядка из >
>
--- группа минимального порядка из >
 >.
Так как >
>.
Так как >
 >---
наследственная формация, то очевидно,
что >
>---
наследственная формация, то очевидно,
что >
 >
--- наследственная формация. А это значит,
что >
>
--- наследственная формация. А это значит,
что >
 >
и >
>
и >
 >.
Покажем, что >
>.
Покажем, что >
 >
--- полный локальный экран, т. е. >
>
--- полный локальный экран, т. е. >
 >
для любого >
>
для любого >
 >
из >
>
из >
 >.
Действительно. Пусть >
>.
Действительно. Пусть >
 >
--- произвольная группа из >
>
--- произвольная группа из >
 >.
Отсюда >
>.
Отсюда >
 >.
Пусть >
>.
Пусть >
 >
--- произвольная >
>
--- произвольная >
 >-группа
из >
>-группа
из >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >.
Отсюда >
>.
Отсюда >
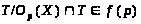 >.
Так как >
>.
Так как >
 >
--- полный экран, то >
>
--- полный экран, то >
 >.
А это значит, что >
>.
А это значит, что >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Отсюда нетрудно заметить, что >
>.
Отсюда нетрудно заметить, что >
 >.
Теперь, согласно теореме 2.2.5, >
>.
Теперь, согласно теореме 2.2.5, >
 >,
где >
>,
где >
 >
--- единственная минимальная нормальная
подгруппа группы >
>
--- единственная минимальная нормальная
подгруппа группы >
 >,
>
>,
>
 >
--- >
>
--- >
 >-группа
и >
>-группа
и >
 >.
Так как >
>.
Так как >
 >
и >
>
и >
 >,
то >
>,
то >
 >.
Отсюда >
>.
Отсюда >
 >.
Противоречие. Итак, >
>.
Противоречие. Итак, >
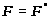 >.
Покажем, что >
>.
Покажем, что >
 >
для любого >
>
для любого >
 >
из >
>
из >
 >.
Пусть >
>.
Пусть >
 >
и >
>
и >
 >
--- >
>
--- >
 >-группа.
Пусть >
>-группа.
Пусть >
 >
--- произвольная >
>
--- произвольная >
 >-подгруппа
из >
>-подгруппа
из >
 >.
Тогда >
>.
Тогда >
 >.
Отсюда >
>.
Отсюда >
 >.
А это значит, что >
>.
А это значит, что >
 >.
Противоречие.
>.
Противоречие.
Достаточность.
Пусть >
 >
--- произвольная минимальная не >
>
--- произвольная минимальная не >
 >-группа.
Так как >
>-группа.
Так как >
 >
разрешима, то по теореме 2.2.5,
>
разрешима, то по теореме 2.2.5,
> >
>
где >
 >
--- >
>
--- >
 >-группа,
>
>-группа,
>
 >.
Согласно условию, >
>.
Согласно условию, >
 >
--- >
>
--- >
 >-группа.
А это значит, что >
>-группа.
А это значит, что >
 >
--- >
>
--- >
 >-замкнутая
группа. Но тогда, >
>-замкнутая
группа. Но тогда, >
 >
--- >
>
--- >
 >-замкнутая
группа. Согласно лемме 4.1.1, >
>-замкнутая
группа. Согласно лемме 4.1.1, >
 >
--- силовская подгруппа группы >
>
--- силовская подгруппа группы >
 >.
Лемма доказана.
>.
Лемма доказана.
1.4 Лемма
[18-A]. Пусть >
 >
--- наследственная насыщенная формация,
>
>
--- наследственная насыщенная формация,
>
 >
--- ее максимальный внутренний локальный
экран. Тогда и только тогда любая
минимальная не >
>
--- ее максимальный внутренний локальный
экран. Тогда и только тогда любая
минимальная не >
 >-группа
бипримарна и >
>-группа
бипримарна и >
 >-замкнута,
где >
>-замкнута,
где >
 >,
когда:
>,
когда:
1) >
 >;
>;
2) формация
>
 >
имеет полный локальный экран >
>
имеет полный локальный экран >
 >
такой, что >
>
такой, что >
 >
и любая группа из >
>
и любая группа из >
 >
является примарной >
>
является примарной >
 >-группой
для любого простого >
>-группой
для любого простого >
 >
из >
>
из >
 >.
>.
Доказательство.
Необходимость. Пусть >
 >
--- произвольная минимальная не >
>
--- произвольная минимальная не >
 >-группа.
Согласно условию, >
>-группа.
Согласно условию, >
 >
--- бипримарная >
>
--- бипримарная >
 >-замкнутая
группа, где >
>-замкнутая
группа, где >
 >.
По лемме 4.1.1, >
>.
По лемме 4.1.1, >
 >.
Согласно лемме 4.1.3, формация >
>.
Согласно лемме 4.1.3, формация >
 >
имеет полный локальный экран >
>
имеет полный локальный экран >
 >
такой, что >
>
такой, что >
 >
и >
>
и >
 >
для любого простого >
>
для любого простого >
 >
из >
>
из >
 >.
Покажем, что любая группа из >
>.
Покажем, что любая группа из >
 >
примарна. Предположим противное. Тогда
существует группа >
>
примарна. Предположим противное. Тогда
существует группа >
 >
и >
>
и >
 >.
Пусть >
>.
Пусть >
 >
--- группа наименьшего порядка такая,
что >
>
--- группа наименьшего порядка такая,
что >
 >.
Очевидно, что >
>.
Очевидно, что >
 >
и >
>
и >
 >.
Нетрудно заметить, что >
>.
Нетрудно заметить, что >
 >
и >
>
и >
 >
имеет единственную минимальную нормальную
подгруппу. Значит, по лемме 2.2.18, существует
точный неприводимый >
>
имеет единственную минимальную нормальную
подгруппу. Значит, по лемме 2.2.18, существует
точный неприводимый >
 >-модуль
>
>-модуль
>
 >,
где >
>,
где >
 >
--- поле из >
>
--- поле из >
 >
элементов.
>
элементов.
Пусть >
 >.
Покажем, что >
>.
Покажем, что >
 >.
Поскольку >
>.
Поскольку >
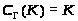 >
и >
>
и >
 >,
то >
>,
то >
 >.
>.
Пусть >
 >
--- собственная подгруппа из >
>
--- собственная подгруппа из >
 >.
Покажем, что >
>.
Покажем, что >
 >.
Пусть >
>.
Пусть >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Пусть >
>.
Пусть >
 >.
Тогда >
>.
Тогда >
 >
--- собственная подгруппа из >
>
--- собственная подгруппа из >
 >.
А это значит, что >
>.
А это значит, что >
 >
и >
>
и >
 >.
Так как >
>.
Так как >
 >
и >
>
и >
 >
--- наследственная формация, то >
>
--- наследственная формация, то >
 >.
Но тогда и >
>.
Но тогда и >
 >,
а значит и >
>,
а значит и >
 >.
>.
Пусть теперь
>
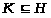 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
и >
>
и >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >.
Итак, >
>.
Итак, >
 >.
Cогласно условию, >
>.
Cогласно условию, >
 >
бипримарна, что невозможно, т. к. >
>
бипримарна, что невозможно, т. к. >
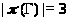 >.
>.
Достаточность.
Пусть >
 >
--- произвольная минимальная не >
>
--- произвольная минимальная не >
 >-группа.
Согласно условию, >
>-группа.
Согласно условию, >
 >
разрешима. По теореме 2.2.5,
>
разрешима. По теореме 2.2.5,
> >
>
где >
 >
--- >
>
--- >
 >-группа,
>
>-группа,
>
 >.
>.
Согласно
условию, >
 >
--- примарная >
>
--- примарная >
 >-группа.
А это значит, что >
>-группа.
А это значит, что >
 >
--- бипримарная >
>
--- бипримарная >
 >-замкнутая
группа. Но тогда >
>-замкнутая
группа. Но тогда >
 >
--- бипримарная >
>
--- бипримарная >
 >-замкнутая
группа. Лемма доказана.
>-замкнутая
группа. Лемма доказана.
2 Критерий
принадлежности групп, факторизуемых
обобщенно субнормальными >
 >-подгруппами,
индексы которых взаимно просты,
наследственно насыщенным формациям
>-подгруппами,
индексы которых взаимно просты,
наследственно насыщенным формациям
В данном
разделе в классе конечных разрешимых
групп получена классификация наследственных
насыщенных формаций >
 >,
замкнутых относительно произведения
обобщенно субнормальных >
>,
замкнутых относительно произведения
обобщенно субнормальных >
 >-подгрупп,
индексы которых взаимно просты.
>-подгрупп,
индексы которых взаимно просты.
2.1 Теорема
[18-A]. Пусть >
 >
--- наследственная насыщенная формация,
>
>
--- наследственная насыщенная формация,
>
 >---
ее максимальный внутренний локальный
экран. Тогда следующие утверждения
эквивалентны:
>---
ее максимальный внутренний локальный
экран. Тогда следующие утверждения
эквивалентны:
1) формация
>
 >
содержит любую группу >
>
содержит любую группу >
 >,
где >
>,
где >
 >
и >
>
и >
 >
--- >
>
--- >
 >-субнормальные
>
>-субнормальные
>
 >-подгруппы
и индексы >
>-подгруппы
и индексы >
 >,
>
>,
>
 >
взаимно просты;
>
взаимно просты;
2) любая
минимальная не >
 >-группа
>
>-группа
>
 >
либо бипримарная >
>
либо бипримарная >
 >-замкнутая
группа >
>-замкнутая
группа >
 >,
либо группа простого порядка;
>,
либо группа простого порядка;
3) формация
>
 >
имеет полный локальный экран >
>
имеет полный локальный экран >
 >
такой, что >
>
такой, что >
 >
и любая группа из >
>
и любая группа из >
 >
является примарной >
>
является примарной >
 >-группой
для любого простого >
>-группой
для любого простого >
 >
из >
>
из >
 >.
>.
Доказательство. Покажем, что из 1) следует 2).
Пусть >
 >
--- произвольная минимальная не >
>
--- произвольная минимальная не >
 >-группа.
Предположим, что >
>-группа.
Предположим, что >
 >,
где >
>,
где >
 >
--- характеристика формации >
>
--- характеристика формации >
 >.
Покажем, что >
>.
Покажем, что >
 >
--- группа простого порядка. Пусть >
>
--- группа простого порядка. Пусть >
 >.
Тогда существует простое число >
>.
Тогда существует простое число >
 >,
>
>,
>
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >,
что невозможно. Итак, >
>,
что невозможно. Итак, >
 >
--- примарная >
>
--- примарная >
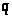 >-группа.
Так как >
>-группа.
Так как >
 >,
то, очевидно, что >
>,
то, очевидно, что >
 >.
>.
Пусть теперь
>
 >.
Рассмотрим случай, когда >
>.
Рассмотрим случай, когда >
 >.
>.
Покажем, что
>
 >
имеет единственную минимальную нормальную
подгруппу >
>
имеет единственную минимальную нормальную
подгруппу >
 >.
Предположим противное. Тогда >
>.
Предположим противное. Тогда >
 >
содержит, по крайней мере, две минимальные
нормальные подгруппы >
>
содержит, по крайней мере, две минимальные
нормальные подгруппы >
 >
и >
>
и >
 >.
Так как >
>.
Так как >
 >,
то в группе >
>,
то в группе >
 >
найдутся максимальные подгруппы >
>
найдутся максимальные подгруппы >
 >
и >
>
и >
 >
такие, что >
>
такие, что >
 >,
>
>,
>
 >.
Так как >
>.
Так как >
 >
и >
>
и >
 >
принадлежат >
>
принадлежат >
 >,
>
>,
>
 >,
>
>,
>
 >,
то >
>,
то >
 >,
>
>,
>
 >.
Так как >
>.
Так как >
 >
--- формация, то >
>
--- формация, то >
 >.
Получили противоречие. Итак, >
>.
Получили противоречие. Итак, >
 >,
где >
>,
где >
 >
--- единственная минимальная нормальная
>
>
--- единственная минимальная нормальная
>
 >-подгруппа
группы >
>-подгруппа
группы >
 >.
>.
Покажем, что
>
 >
--- примарная >
>
--- примарная >
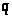 >-группа,
где >
>-группа,
где >
 >.
Предположим, что существуют простые
числа >
>.
Предположим, что существуют простые
числа >
 >,
где >
>,
где >
 >.
Тогда в >
>.
Тогда в >
 >
найдутся максимальные подгруппы >
>
найдутся максимальные подгруппы >
 >
и >
>
и >
 >
такие, что >
>
такие, что >
 >
--- >
>
--- >
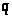 >-число,
>
>-число,
>
 >
--- >
>
--- >
 >-число.
Рассмотрим подгруппы >
>-число.
Рассмотрим подгруппы >
 >
и >
>
и >
 >.
Очевидно, что индексы >
>.
Очевидно, что индексы >
 >
и >
>
и >
 >
взаимно просты. Так как >
>
взаимно просты. Так как >
 >
и >
>
и >
 >,
то >
>,
то >
 >.
Согласно лемме 3.1.4, подгруппы >
>.
Согласно лемме 3.1.4, подгруппы >
 >
и >
>
и >
 >
>
>
>
 >-субнормальны
в >
>-субнормальны
в >
 >.
Так как >
>.
Так как >
 >
--- минимальная не >
>
--- минимальная не >
 >-группа,
>
>-группа,
>
 >
и >
>
и >
 >
--- собственные подгруппы группы >
>
--- собственные подгруппы группы >
 >,
то >
>,
то >
 >
и >
>
и >
 >.
Так как >
>.
Так как >
 >,
то согласно условию, >
>,
то согласно условию, >
 >.
Получили противоречие.
>.
Получили противоречие.
Покажем, что
>
 >
--- >
>
--- >
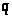 >-группа,
где >
>-группа,
где >
 >.
Предположим, что >
>.
Предположим, что >
 >.
Так как >
>.
Так как >
 >,
то согласно лемме 3.1.4, >
>,
то согласно лемме 3.1.4, >
 >
--- >
>
--- >
 >-субнормальная
подгуппа группы >
>-субнормальная
подгуппа группы >
 >.
Рассмотрим подгруппу >
>.
Рассмотрим подгруппу >
 >.
Так как >
>.
Так как >
 >
--- собственная подгруппа >
>
--- собственная подгруппа >
 >
и >
>
и >
 >,
то >
>,
то >
 >.
Согласно лемме 3.1.4, >
>.
Согласно лемме 3.1.4, >
 >
--- >
>
--- >
 >-субнормальная
подгруппа >
>-субнормальная
подгруппа >
 >.
Очевидно, что >
>.
Очевидно, что >
 >
--- >
>
--- >
 >-субнормальная
подгруппа >
>-субнормальная
подгруппа >
 >.
По лемме 3.1.4, >
>.
По лемме 3.1.4, >
 >
--- >
>
--- >
 >-субнормальная
подгруппа группы >
>-субнормальная
подгруппа группы >
 >.
Так как >
>.
Так как >
 >,
то из >
>,
то из >
 >
и условия теоремы следует, что >
>
и условия теоремы следует, что >
 >.
Получили противоречие. Итак, >
>.
Получили противоречие. Итак, >
 >
--- >
>
--- >
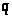 >-группа.
Тогда >
>-группа.
Тогда >
 >
--- бипримарная >
>
--- бипримарная >
 >-замкнутая
группа, где >
>-замкнутая
группа, где >
 >.
>.
Пусть >
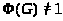 >.
Рассмотрим фактор-группу >
>.
Рассмотрим фактор-группу >
 >.
Так как >
>.
Так как >
 >,
то, как показано выше, >
>,
то, как показано выше, >
 >
--- бипримарная >
>
--- бипримарная >
 >-замкнутая
группа. Отсюда следует, что >
>-замкнутая
группа. Отсюда следует, что >
 >
--- бипримарная >
>
--- бипримарная >
 >-замкнутая
группа.
>-замкнутая
группа.
Из леммы 4.1.4 следует, что утверждение 3) следует из 2).
Покажем, что из 3) следует 1).
Пусть >
 >
--- группа наименьшего порядка такая,
что >
>
--- группа наименьшего порядка такая,
что >
 >,
где >
>,
где >
 >
и >
>
и >
 >
--- >
>
--- >
 >-субнормальные
>
>-субнормальные
>
 >-подгруппы
группы >
>-подгруппы
группы >
 >
взаимно простых индексов, то >
>
взаимно простых индексов, то >
 >.
Так как >
>.
Так как >
 >
--- разрешимая группа и >
>
--- разрешимая группа и >
 >,
где >
>,
где >
 >,
то нетрудно заметить, что >
>,
то нетрудно заметить, что >
 >,
где >
>,
где >
 >
и >
>
и >
 >
--- холловские подгруппы группы >
>
--- холловские подгруппы группы >
 >,
>
>,
>
 >
и >
>
и >
 >,
>
>,
>
 >,
где >
>,
где >
 >,
>
>,
>
 >
--- некоторые элементы группы >
>
--- некоторые элементы группы >
 >.
>.
Пусть >
 >
--- собственная подгруппа группы >
>
--- собственная подгруппа группы >
 >.
Покажем, что >
>.
Покажем, что >
 >.
Так как >
>.
Так как >
 >
--- разрешимая группа, то согласно теореме
Ф. Холла [63], >
>
--- разрешимая группа, то согласно теореме
Ф. Холла [63], >
 >,
где >
>,
где >
 >,
>
>,
>
 >,
где >
>,
где >
 >,
>
>,
>
 >
--- некоторые элементы из >
>
--- некоторые элементы из >
 >.
Согласно лемме 3.1.4, >
>.
Согласно лемме 3.1.4, >
 >
и >
>
и >
 >
--- >
>
--- >
 >-субнормальные
подгруппы группы >
>-субнормальные
подгруппы группы >
 >.
Так как >
>.
Так как >
 >
и >
>
и >
 >,
а >
>,
а >
 >
--- наследственная формация, то >
>
--- наследственная формация, то >
 >
и >
>
и >
 >
--- >
>
--- >
 >-субнормальные
подгруппы >
>-субнормальные
подгруппы >
 >
и >
>
и >
 >
соответственно. Согласно лемме 3.1.4,
нетрудно показать, что >
>
соответственно. Согласно лемме 3.1.4,
нетрудно показать, что >
 >
и >
>
и >
 >
--- >
>
--- >
 >-субнормальные
подгруппы группы >
>-субнормальные
подгруппы группы >
 >,
а значит, согласно лемме 3.1.4 и в >
>,
а значит, согласно лемме 3.1.4 и в >
 >.
Так как >
>.
Так как >
 >,
то по индукции, получаем, что >
>,
то по индукции, получаем, что >
 >.
А это значит, что >
>.
А это значит, что >
 >
--- минимальная не >
>
--- минимальная не >
 >-группа.
>-группа.
Если >
 >
--- группа простого порядка, то ее нельзя
представить в виде произведения
собственных подгрупп взаимно простых
индексов.
>
--- группа простого порядка, то ее нельзя
представить в виде произведения
собственных подгрупп взаимно простых
индексов.
Пусть >
 >
--- бипримарная группа. Тогда согласно
лемме 4.1.4, >
>
--- бипримарная группа. Тогда согласно
лемме 4.1.4, >
 >.
Согласно лемме 4.1.1, >
>.
Согласно лемме 4.1.1, >
 >.
А это значит, что все подгруппы группы
>
>.
А это значит, что все подгруппы группы
>
 >,
содержащие >
>,
содержащие >
 >
>
>
>
 >-абнормальны,
т. е. группа >
>-абнормальны,
т. е. группа >
 >
не представима в виде произведения
собственных >
>
не представима в виде произведения
собственных >
 >-субнормальных
>
>-субнормальных
>
 >-подгрупп
взаимно простых индексов. Получили
противоречие. Теорема доказана.
>-подгрупп
взаимно простых индексов. Получили
противоречие. Теорема доказана.
Напомним,
что формация >
 >
называется 2-кратно насыщенной, если
она имеет локальный экран >
>
называется 2-кратно насыщенной, если
она имеет локальный экран >
 >
такой, что >
>
такой, что >
 >
--- насыщенная формация для любого
простого числа >
>
--- насыщенная формация для любого
простого числа >
 >
из >
>
из >
 >.
>.
Следующая теорема доказана в классе конечных разрешимых групп.
2.2 Теорема
[18-A]. Пусть >
 >
--- наследственная 2-кратно насыщенная
формация. Тогда следующие утверждения
эквивалентны:
>
--- наследственная 2-кратно насыщенная
формация. Тогда следующие утверждения
эквивалентны:
1) формация
>
 >
содержит любую группу >
>
содержит любую группу >
 >,
где >
>,
где >
 >
и >
>
и >
 >
--- >
>
--- >
 >-субнормальные
>
>-субнормальные
>
 >-подгруппы
из >
>-подгруппы
из >
 >
взаимно простых индексов;
>
взаимно простых индексов;
2) >
 >
--- формация Шеметкова;
>
--- формация Шеметкова;
3) формация
>
 >
содержит любую группу >
>
содержит любую группу >
 >,
где >
>,
где >
 >
и >
>
и >
 >
--- >
>
--- >
 >-субнормальные
>
>-субнормальные
>
 >-подгруппы
из >
>-подгруппы
из >
 >;
>;
4) >
 >.
>.
Доказательство. Покажем, что из 1) следует 2).
Пусть >
 >
--- произвольная минимальная не >
>
--- произвольная минимальная не >
 >-группа.
Рассмотрим случай, когда >
>-группа.
Рассмотрим случай, когда >
 >.
Как и в теореме 4.2.1 можно показать, что
либо >
>.
Как и в теореме 4.2.1 можно показать, что
либо >
 >
--- группа простого порядка >
>
--- группа простого порядка >
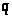 >,
где >
>,
где >
 >,
либо >
>,
либо >
 >,
где >
>,
где >
 >
и >
>
и >
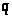 >
из >
>
из >
 >.
А также нетрудно показать, что >
>.
А также нетрудно показать, что >
 >
--- единственная минимальная нормальная
подгруппа группы >
>
--- единственная минимальная нормальная
подгруппа группы >
 >.
А это значит, что >
>.
А это значит, что >
 >.
Пусть >
>.
Пусть >
 >
--- максимальный внутренний локальный
экран формации >
>
--- максимальный внутренний локальный
экран формации >
 >.
Если >
>.
Если >
 >,
то из полноты экрана >
>,
то из полноты экрана >
 >
следует, что >
>
следует, что >
 >.
Так как >
>.
Так как >
 >
--- внутренний экран, то >
>
--- внутренний экран, то >
 >.
А это значит, что >
>.
А это значит, что >
 >.
Противоречие. Итак, >
>.
Противоречие. Итак, >
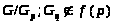 >.
>.
Покажем, что
>
 >.
Предположим, что это не так. Тогда в >
>.
Предположим, что это не так. Тогда в >
 >
найдется неединичная собственная
подгруппа >
>
найдется неединичная собственная
подгруппа >
 >.
Рассмотрим подгруппу >
>.
Рассмотрим подгруппу >
 >.
Так как >
>.
Так как >
 >
--- минимальная не >
>
--- минимальная не >
 >-группа
и >
>-группа
и >
 >
--- собственная подгруппа >
>
--- собственная подгруппа >
 >,
то >
>,
то >
 >.
Покажем, что >
>.
Покажем, что >
 >.
Если это не так, то в >
>.
Если это не так, то в >
 >
существует неединичная нормальная
>
>
существует неединичная нормальная
>
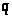 >-подгруппа
>
>-подгруппа
>
 >.
Тогда >
>.
Тогда >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >,
что невозможно. Согласно лемме 2.2.12, >
>,
что невозможно. Согласно лемме 2.2.12, >
 >.
Отсюда >
>.
Отсюда >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >.
А это значит, что >
>.
А это значит, что >
 >.
Так как >
>.
Так как >
 >
--- насыщенная формация, то >
>
--- насыщенная формация, то >
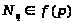 >.
Следовательно, >
>.
Следовательно, >
 >,
что невозможно. Итак, >
>,
что невозможно. Итак, >
 >,
значит, >
>,
значит, >
 >
--- группа Шмидта. Итак, >
>
--- группа Шмидта. Итак, >
 >
--- группа Шмидта. По лемме 3.1.1, >
>
--- группа Шмидта. По лемме 3.1.1, >
 >
--- группа Шмидта.
>
--- группа Шмидта.
Тот факт, что
из 2) >
 >
3) следует из теоремы 2.2.19; 3) >
>
3) следует из теоремы 2.2.19; 3) >
 >
4) следует из теоремы 2.2.10; 4) >
>
4) следует из теоремы 2.2.10; 4) >
 >
1) следует из теоремы 2.2.10. Теорема
доказана.
>
1) следует из теоремы 2.2.10. Теорема
доказана.
Очевидно,
что любая сверхрадикальная формация >
 >
содержит любую группу >
>
содержит любую группу >
 >,
где >
>,
где >
 >
и >
>
и >
 >
>
>
>
 >-субнормальны
в >
>-субнормальны
в >
 >
и принадлежат >
>
и принадлежат >
 >
и имеют взаимно простые индексы в >
>
и имеют взаимно простые индексы в >
 >.
>.
Следующий
пример показывает, что существует
несверхрадикальная наследственная
насыщенная формация >
 >,
содержащая любую группу >
>,
содержащая любую группу >
 >,
где >
>,
где >
 >
и >
>
и >
 >
>
>
>
 >-субнормальны
в >
>-субнормальны
в >
 >
и принадлежат >
>
и принадлежат >
 >
и имеют взаимно простые индексы в >
>
и имеют взаимно простые индексы в >
 >.
>.
2.3 Пример.
Пусть >
 >
--- формация всех сверхразрешимых групп,
а >
>
--- формация всех сверхразрешимых групп,
а >
 >
--- формация всех >
>
--- формация всех >
 >-групп,
где >
>-групп,
где >
 >,
>
>,
>
 >
и >
>
и >
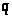 >
--- различные простые числа. Рассмотрим
формацию >
>
--- различные простые числа. Рассмотрим
формацию >
 >.
Так как существуют минимальные не
>
>.
Так как существуют минимальные не
>
 >-группы,
которые не являются либо группой Шмидта,
либо группой простого порядка, то >
>-группы,
которые не являются либо группой Шмидта,
либо группой простого порядка, то >
 >
не является формацией Шеметкова. Так
как >
>
не является формацией Шеметкова. Так
как >
 >,
то согласно теореме 3.3.9, формация >
>,
то согласно теореме 3.3.9, формация >
 >
не является сверхрадикальной формацией.
>
не является сверхрадикальной формацией.
С другой
стороны хорошо известно, что любая
минимальная несверхразрешимая группа
>
 >
>
>
>
 >-замкнута,
где >
>-замкнута,
где >
 >.
Очевидно, что любая минимальная не
>
>.
Очевидно, что любая минимальная не
>
 >-группа
>
>-группа
>
 >
является либо группой простого порядка,
либо бипримарной >
>
является либо группой простого порядка,
либо бипримарной >
 >-замкнутой
группой, где >
>-замкнутой
группой, где >
 >.
Теперь из теоремы 4.2.1 следует, что >
>.
Теперь из теоремы 4.2.1 следует, что >
 >
содержит любую группу >
>
содержит любую группу >
 >,
где >
>,
где >
 >,
>
>,
>
 >
и >
>
и >
 >
принадлежат >
>
принадлежат >
 >
и >
>
и >
 >
и >
>
и >
 >
--- субнормальны в >
>
--- субнормальны в >
 >.
>.
Заключение
В главе 1 доказаны леммы, которые используются для доказательства основных результатов главы 2.
В главе 2
важную роль сыграл метод экстремальных
классов, разработанный в работе Картера,
Фишера, Хоукса [55] и метод критических
групп, разработанный В.Н. Семенчуком в
работе [19]. С помощью этих методов в
классе конечных разрешимых групп
получено описание наследственных
насыщенных формаций >
 >,
содержащих любую группу >
>,
содержащих любую группу >
 >,
где >
>,
где >
 >,
>
>,
>
 >
и >
>
и >
 >
принадлежат >
>
принадлежат >
 >
и >
>
и >
 >
и >
>
и >
 >
--- >
>
--- >
 >-субнормальны
в >
>-субнормальны
в >
 >,
теорема 2.1 .
>,
теорема 2.1 .
Доказано,
что любая разрешимая >
 >
--- наследственная 2-кратно насыщенная
формация, обладающая отмеченным выше
свойством, является сверхрадикальной,
теорема 2.2 .
>
--- наследственная 2-кратно насыщенная
формация, обладающая отмеченным выше
свойством, является сверхрадикальной,
теорема 2.2 .
Список использованных источников
1. Васильев, А.Ф. О максимальной наследственной подформации локальной формации / А.Ф. Васильев // Вопросы алгебры: межведомств. сб. / Мин-во народного обр. БССР, Гомельский гос. ун-т; редкол.: Л.А. Шеметков [и др.]. -- Минск: Университетское, 1990. -- Вып. 5. -- С. 39--45.
2. Васильев, А.Ф. О решетках подгрупп конечных групп / А.Ф. Васильев, С.Ф. Каморников, В.Н. Семенчук // Бесконечные группы и примыкающие алгебраические системы / Ин-т математики Акад. Украины; редкол.: Н.С. Черников [и др.]. -- Киев, 1993. -- С. 27--54.
3. Васильев,
А.Ф. О влиянии примарных >
 >-субнормальных
подгрупп на строение группы / А.Ф. Васильев
// Вопросы алгебры: межведомств. сб. /
Мин-во обр. и науки Республики Беларусь,
Гомельский гос. ун-т им. Ф. Скорины;
редкол.: Л.А. Шеметков [и др.]. -- Гомель,
1995. -- Вып. 8. -- С. 31--39.
>-субнормальных
подгрупп на строение группы / А.Ф. Васильев
// Вопросы алгебры: межведомств. сб. /
Мин-во обр. и науки Республики Беларусь,
Гомельский гос. ун-т им. Ф. Скорины;
редкол.: Л.А. Шеметков [и др.]. -- Гомель,
1995. -- Вып. 8. -- С. 31--39.
4. Васильева,
Т.И. О конечных группах с >
 >-достижимыми
силовскими подгруппами / Т.И. Васильева,
А.И. Прокопенко. -- Гомель, 2006. -- 18 с. --
(Препринт / Гомельский гос. ун-т им. Ф.
Скорины; № 4).
>-достижимыми
силовскими подгруппами / Т.И. Васильева,
А.И. Прокопенко. -- Гомель, 2006. -- 18 с. --
(Препринт / Гомельский гос. ун-т им. Ф.
Скорины; № 4).
5. Ведерников, В.А. О локальных формациях конечных групп / В.А. Ведерников // Матем. заметки. -- 1989. -- Т. 46, № 3. -- С. 32--37.
6. Казарин, Л.С. Признаки непростоты факторизуемых групп / Л.С. Казарин // Известия АН СССР. -- 1980. -- Т. 44, № 2. -- С. 288--308.
7. Казарин, Л.С. О произведении конечных групп / Л.С. Казарин // ДАН СССР. -- 1983. -- Т. 269, № 3. -- С. 528--531.
8. Каморников, С.Ф. О некоторых свойствах формаций квазинильпотентных групп / С.Ф. Каморников // Матем. заметки. -- 1993. -- Т. 53, № 2. -- С. 71--77.
9. Каморников, С.Ф. О двух проблемах Л.А. Шеметкова / С.Ф. Каморников // Сибир. мат. журнал. -- 1994. -- Т. 35, № 4. -- С. 801--812.
10. Коуровская тетрадь (нерешенные вопросы теории групп) // Институт математики СО АН СССР. -- Новосибирск, 1992. -- 172 с.
11. Коуровская тетрадь (нерешенные вопросы теории групп) // Институт математики СО РАН. -- Новосибирск, 1999. -- 146 с.
12. Легчекова, Е.В. Конечные группы с заданными слабо квазинормальными подгруппами / Е.В. Легчекова, А.Н. Скиба, О.В. Титов // Доклады НАН Беларуси. -- 2007. -- Т. 51, № 1. -- С. 27--33.
13. Монахов, В.С. Произведение конечных групп, близких к нильпотентным / В.С. Монахов // Конечные группы. -- 1975. -- С. 70--100.
14. Монахов, В.С. О произведении двух разрешимых групп с максимальным пересечением факторов / В.С. Монахов // Вопросы алгебры: межведомств. сб. / Мин-во высш. и ср. спец. обр. БССР, Гомельский гос. ун-т; редкол.: Л.А. Шеметков [и др.]. -- Минск: Университетское, 1985. -- Вып. 1. -- С. 54--57.
15. Мокеева,
С.А. Конечные группы с перестановочными
>
 >-субнормальными
(>
>-субнормальными
(> >-достижимыми)
подгруппами / С.А. Мокеева. -- Гомель,
2003. -- 25 с. -- (Препринт / Гомельский гос.
ун-т им. Ф. Скорины; № 56).
>-достижимыми)
подгруппами / С.А. Мокеева. -- Гомель,
2003. -- 25 с. -- (Препринт / Гомельский гос.
ун-т им. Ф. Скорины; № 56).
16. Прокопенко,
А.И. О конечных группах с >
 >-достижимыми
силовскими подгруппами / А.И. Прокопенко
// Известия Гомельского гос. ун-та им. Ф.
Скорины. -- 2004. -- № 6 (27). -- С. 101--103.
>-достижимыми
силовскими подгруппами / А.И. Прокопенко
// Известия Гомельского гос. ун-та им. Ф.
Скорины. -- 2004. -- № 6 (27). -- С. 101--103.
17. Семенчук,
В.Н. О минимальных не >
 >-группах
/ В.Н. Семенчук // ДАН БССР. -- 1978. -- № 7. --
С. 596--599.
>-группах
/ В.Н. Семенчук // ДАН БССР. -- 1978. -- № 7. --
С. 596--599.
18. Семенчук, В.Н. Конечные группы с заданными свойствами подгрупп / В.Н. Семенчук // ДАН БССР. -- 1979. -- № 1. -- С. 11--15.
19. Семенчук,
В.Н. Минимальные не >
 >-группы
/ В.Н. Семенчук // Алгебра и логика. -- 1979.
-- Т. 18, № 3. -- С. 348--382.
>-группы
/ В.Н. Семенчук // Алгебра и логика. -- 1979.
-- Т. 18, № 3. -- С. 348--382.
20. Семенчук,
В.Н. Конечные группы с системой минимальных
не >
 >-подгрупп
/ В.Н. Семенчук // Подгрупповое строение
конечных групп: Тр. / Ин-т математики АН
БССР. -- Минск: Наука и техника, 1981. -- С.
138--149.
>-подгрупп
/ В.Н. Семенчук // Подгрупповое строение
конечных групп: Тр. / Ин-т математики АН
БССР. -- Минск: Наука и техника, 1981. -- С.
138--149.
21. Семенчук,
В.Н. Минимальные не >
 >-группы
/ В.Н. Семенчук // Исследование нормального
и подгруппового строения конечных
групп: Тр. / Ин-т математики АН БССР. --
Минск: Наука и техника, 1984. -- С. 170--175.
>-группы
/ В.Н. Семенчук // Исследование нормального
и подгруппового строения конечных
групп: Тр. / Ин-т математики АН БССР. --
Минск: Наука и техника, 1984. -- С. 170--175.
22. Семенчук,
В.Н. Характеризация локальных формаций
>
 >
по заданным свойствам минимальных не
>
>
по заданным свойствам минимальных не
>
 >-групп
/ В.Н. Семенчук, А.Ф. Васильев // Исследование
нормального и подгруппового строения
конечных групп: Тр. / Ин-т математики АН
БССР. -- Минск: Наука и техника, 1984. -- С.
175--181.
>-групп
/ В.Н. Семенчук, А.Ф. Васильев // Исследование
нормального и подгруппового строения
конечных групп: Тр. / Ин-т математики АН
БССР. -- Минск: Наука и техника, 1984. -- С.
175--181.
23. Семенчук,
В.Н. Описание разрешимых минимальных
не >
 >-групп
для произвольной тотально локальной
формации / В.Н. Семенчук // Матем. заметки.
-- 1988. -- Т. 43, № 4. -- С. 251--260.
>-групп
для произвольной тотально локальной
формации / В.Н. Семенчук // Матем. заметки.
-- 1988. -- Т. 43, № 4. -- С. 251--260.
24. Семенчук,
В.Н. О разрешимых минимальных не >
 >-группах
/ В.Н. Семенчук // Вопросы алгебры. -- Минск:
Университетское, 1987. -- Вып. 3. -- С. 16--21.
>-группах
/ В.Н. Семенчук // Вопросы алгебры. -- Минск:
Университетское, 1987. -- Вып. 3. -- С. 16--21.
25. Семенчук,
В.Н. Роль минимальных не >
 >-групп
в теории формаций / В.Н. Семенчук // Матем.
заметки. -- 1991. -- Т. 98, № 1. -- С. 110--115.
>-групп
в теории формаций / В.Н. Семенчук // Матем.
заметки. -- 1991. -- Т. 98, № 1. -- С. 110--115.
26. Семенчук,
В.Н. Конечные группы с >
 >-абнормальными
или >
>-абнормальными
или >
 >-субнормальными
подгруппами / В.Н. Семенчук // Матем.
заметки. -- 1994. -- Т. 56, № 6. -- С. 111--115.
>-субнормальными
подгруппами / В.Н. Семенчук // Матем.
заметки. -- 1994. -- Т. 56, № 6. -- С. 111--115.
27. Семенчук, В.Н. Разрешимые тотально локальные формации / В.Н. Семенчук // Сибир. мат. журн. -- 1995. -- Т. 36, № 4. -- С. 861--872.
28. Семенчук,
В.Н. Разрешимые >
 >-радикальные
формации / В.Н. Семенчук // Матем. заметки.
-- 1996. -- Т. 59, № 2. -- С. 261--266.
>-радикальные
формации / В.Н. Семенчук // Матем. заметки.
-- 1996. -- Т. 59, № 2. -- С. 261--266.
29. Семенчук, В.Н. Об одной проблеме в теории формаций / В.Н. Семенчук // Весцi АН Беларусi. -- 1996. -- № 3. -- С. 25--29.
30. Семенчук, В.Н. О разрешимых тотально локальных формациях / В.Н. Семенчук // Вопросы алгебры. -- 1997. -- № 11. -- С. 109--115.
31. Семенчук,
В.Н., Поляков Л.Я. Характеризация
минимальных не >
 >-групп
/ В.Н. Семенчук // Известия высших учебных
заведений. -- 1998. -- № 4 (431). -- С. 1--4.
>-групп
/ В.Н. Семенчук // Известия высших учебных
заведений. -- 1998. -- № 4 (431). -- С. 1--4.
32. Семенчук, В.Н. Классификация локальных наследственных формаций критические группы которых бипримарны / В.Н. Семенчук // Известия Гомельского гос. ун-та им. Ф. Скорины. -- 1999. -- № 1 (15). -- С. 153--162.
33. Семенчук, В.Н. Сверхрадикальные формации / В.Н. Семенчук, Л.А. Шеметков // Доклады НАН Беларуси. -- 2000. -- Т. 44, № 5. -- С. 24--26.
34. Семенчук,
В.Н. Конечные группы, факторизуемые
>
 >-достижимыми
подгруппами / В.Н. Семенчук, С.А. Мокеева
// Известия Гомельского гос. ун-та им. Ф.
Скорины. -- 2002. -- № 5 (14). -- С. 47--49.
>-достижимыми
подгруппами / В.Н. Семенчук, С.А. Мокеева
// Известия Гомельского гос. ун-та им. Ф.
Скорины. -- 2002. -- № 5 (14). -- С. 47--49.
35. Скиба, А.Н. Об одном классе локальных формаций конечных групп / А.Н. Скиба // ДАН БССР. -- 1990. -- Т. 34, № 11. -- С. 382--385.
36. Скиба, А.Н. Алгебра формаций / А.Н. Скиба. -- Минск: Беларуская навука, 1997. -- 240 с.
37. Старостин, А.И. О минимальных группах, не обладающих данным свойством / А.И. Старостин // Матем. заметки. -- 1968. -- Т. 3, № 1. -- С. 33--37.
38. Тютянов,
В.Н. Факторизации >
 >-нильпотентными
сомножителями / В.Н. Тютянов // Матем. сб.
-- 1996. -- Т. 187, № 9. -- С. 97--102.
>-нильпотентными
сомножителями / В.Н. Тютянов // Матем. сб.
-- 1996. -- Т. 187, № 9. -- С. 97--102.
39. Чунихин, С.А. О специальных группах / С.А. Чунихин // Матем. сб. -- 1929. -- Т. 36, № 2. -- С. 135--137.
40. Чунихин, С.А. О специальных группах / С.А. Чунихин // Матем. сб. -- 1933. -- Т. 40, № 1. -- С. 39--41.
41. Чунихин, С.А. О группах с наперед заданными подгруппами / С.А. Чунихин // Матем. сб. -- 1938. -- Т. 4 (46), № 3. -- С. 521--530.
42. Чунихин, С.А. О существовании подгрупп у конечной группы / С.А. Чунихин // Труды семинара по теории групп. -- ГОНТИ, М.--Л. -- 1938. -- С. 106--125.
43. Чунихин, С.А. Подгруппы конечных групп / С.А. Чунихин. -- Минск: Наука и техника, 1964. -- 158 с.
44. Шеметков, Л.А. Формации конечных групп / Л.А. Шеметков. -- М.: Наука, 1978. -- 272 с.
45. Шеметков, Л.А. Экраны произведения формаций / Л.А. Шеметков // ДАН БССР. -- 1981. -- Т. 25, № 8. -- С. 677--680.
46. Шеметков, Л.А. О произведении формаций / Л.А. Шеметков // ДАН БССР. -- 1984. -- Т. 28, № 2. -- С. 101--103.
47. Шеметков, Л.А. Формации алгебраических систем / Л.А. Шеметков, А.Н. Скиба. -- М.: Наука, 1989. -- 256 с.
48. Шмидт, О.Ю. Группы, все подгруппы которых специальные / О.Ю. Шмидт // Матем. сб. -- 1924. -- Т. 31, № 3. -- С. 366--372.
49.
Ballester-Bolinches, A. On the lattice of >
 >-sub>normal
sub>groups / A. Ballester-Bolinches, К. Doerk, M.D. Perez-Ramos // J.
Algebra. -- 1992. -- Vol. 148, № 2. -- P. 42--52.
>-sub>normal
sub>groups / A. Ballester-Bolinches, К. Doerk, M.D. Perez-Ramos // J.
Algebra. -- 1992. -- Vol. 148, № 2. -- P. 42--52.
50.
Ballester-Bolinches, A. On >
 >-critical
groups / A. Ballester-Bolinches, M.D. Perez-Ramos // J. Algebra. --
1995. -- Vol. 174. -- P. 948--958.
>-critical
groups / A. Ballester-Bolinches, M.D. Perez-Ramos // J. Algebra. --
1995. -- Vol. 174. -- P. 948--958.
51. Ballester-Bolinches, A. Two questions of L.A. Shemetkov on critical groups / A. Ballester-Bolinches, M.D. Perez-Ramos // J. Algebra. -- 1996. -- Vol. 179. -- P. 905--917.
52. Ballester-Bolinches, A. Classes of Finite Groups / A. Ballester-Bolinches, L.M. Ezquerro. -- Springer, 2006. -- 385 p.
53. Bryce, R.A. Fitting formations of finite soluble groups / R.A. Bryce, J. Cossey // Math. Z. -- 1972. -- Bd. 127, № 3. -- S. 217--233.
54. Carter, R.O. The
>
 >-normalizers
of a finite soluble group / R. Carter, T. Hawkes // J. Algebra. --
1967. -- Vol. 5, № 2. -- Р. 175--202.
>-normalizers
of a finite soluble group / R. Carter, T. Hawkes // J. Algebra. --
1967. -- Vol. 5, № 2. -- Р. 175--202.
55. Carter, R. Extreme classes of a finite soluble groups / R. Carter, B. Fisсher, T. Hawkes // J. Algebra. -- 1968. -- Vol. 9, № 3. -- P. 285--313.
56. Doerk, K. Minimal nicht Uberauflosbare, endliche Gruppen / K. Doerk // Math. Z. -- 1966. -- Vol. 91. -- P. 198--205.
57. Doerk, K. Finite soluble groups / K. Doerk, T. Hаwkes. -- Berlin -- New York: Walter de Gruyter, 1992. -- 891 p.
58. Fisman, E. On product of two finite solvable groups / E. Fisman // J. Algebra. -- 1983. -- Vol. 80, № 2. -- P. 517--536.
59. Gaschutz, W. Zur Theorie der endlichen auflosbaren Gruppen // Math. Z. -- 1963. -- Vol. 80, № 4. -- P. 300--305.
60. Guo, W. The Theory of Classes of Groups / W. Guo. -- Dordrecht -- Boston -- London: Kluwer Academic Publishers, 2000. -- 257 p.
61. Guo, W. X-semipermutable sub>groups of finite groups / W. Guo, K.P. Shum, A.N. Skiba // J. Algebra. -- 2007. -- Vol. 315. -- P. 31--41.
62. Hall, P. A note on soluble groups / P. Hall // Proc. London Math. Soc. -- 1928. -- Vol. 3. -- P. 98--105.
63. Hall, P. On the Sylow systems of a soluble group / P. Hall // Proc. London Math. Soc. -- 1937. -- Vol. 43. -- P. 316--323.
64. Hawkes, T. On Fitting formations / T. Hawkes // Math. Z. -- 1970. -- Vol. 117. -- P. 177--182.
65. Huppert, B. Normalteiler und maximal Untergruppen endlichen Gruppen / B. Huppert // Math. Z. -- 1954. -- Vol. 60. -- P. 409--434.
66. Ito, N. Note on (LN)-groups of finite order / N. Ito // Kodai Math. Seminar Report. -- 1951. -- Vol. 1--2. -- P. 1--6.
67. Kazarin, L.S. Product of two solvable sub>groups / L.S. Kazarin // Comm. Algebra. -- 1986. -- Vol. 14, № 6. -- P. 1001--1066.
68. Kegel, O.H. Produkte nilpotenter Gruppen // Arch. Math. -- 1961. -- Vol. 12, № 2. -- P. 90--93.
69. Kegel, O.H. Untergruppenverbande endlicher Gruppen, die sub>normalteilerverband echt enthalten / O.H. Kegel // Arch. Math. -- 1978. -- Bd. 30, № 3. -- S. 225--228.
70. Miller, G.A. Nonabelian groups in which every sub>group is abelian / G.A. Miller, H.C. Moreno // Trans. Amer. Math. Soc. -- 1903. -- Vol. 4. -- P. 398--404.
71. Semenchuk, V.N.
Finite groups with permutable >
 >-sub>normal
and >
>-sub>normal
and >
 >-accessible
sub>groups / V.N. Semenchuk, S.A. Mokeeva // 4th International
Algebraic Conference in Ukraine. Abstracts, August 4--9. -- 2003. --
P. 153--154.
>-accessible
sub>groups / V.N. Semenchuk, S.A. Mokeeva // 4th International
Algebraic Conference in Ukraine. Abstracts, August 4--9. -- 2003. --
P. 153--154.
72. Thompson, J.G. Nonsolvable finite groups all of whose local sub>groups are solvable / J.G. Thompson // Bull. Amer. Math. Soc. -- 1968. -- Vol. 74. -- P. 383--437.
73. Wielandt, H. Eine Verallgemeinerung der invarianten Untergruppen // H. Wielandt // Math. Z. -- 1939. -- Bd. 45. -- S. 209--244.
74. Wielandt, H. Uber den Normalisator der sub>normalen Untergruppen // H. Wielandt // Math. Z. -- 1958. -- Bd. 69, № 8. -- S. 463--465.
75. Wielandt, H. Uber das Produkt von nilpotenten Gruppen / H. Wielandt // Illinois Journ. -- 1958. -- Vol. 2, № 4B. -- P. 611--618.