Классификация групп с перестановочными обобщенно максимальными подгруппами
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет им. Ф. Скорины»
Математический факультет
Кафедра алгебры и геометрии
Курсовая работа
Классификация групп с перестановочными обобщенно максимальными подгруппами
Исполнитель:
Студентка группы М-32 Лапухова А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент Скиба М.Т.
Гомель 2005
Содержание
Перечень условных обозначений
Введение
1. Классификация групп с перестановочными обобщенно максимальными подгруппами
>2. Группы с 010009000003a400000002001c0000000000030000001e000500000009020000000005000000020101000000050000000102ffffff00050000002e0118000000050000000c02a001c001050000000b02000000001200000026060f001a00ffffffff000010000000c0ffffffc6ffffff80010000660100000b00000026060f000c004d61746854797065000020001c000000fb0280fe0000000000009001010000cc0402001054696d6573204e657720526f6d616e00b8aef377c1aef3772040f57779316633040000002d01000008000000320a600158000100000058ff0a00000026060f000a00ffffffff0100000000001c000000fb021000070000000000bc02000000cc0102022253797374656d00009b430a9590e21100b8aef377c1aef3772040f57779316633040000002d01010004000000f0010000040000002701ffff030000000000-перестановочными 010009000003a400000002001c0000000000030000001e000500000009020000000005000000020101000000050000000102ffffff00050000002e0118000000050000000c02a001e000050000000b02000000001200000026060f001a00ffffffff000010000000c0ffffffe6ffffffa0000000860100000b00000026060f000c004d61746854797065000030001c000000fb0280fe0000000000009001010000cc0402001054696d6573204e657720526f6d616e00b8aef377c1aef3772040f577ac296642040000002d01000008000000320a40012e000100000069430a00000026060f000a00ffffffff0100000000001c000000fb021000070000000000bc02000000cc0102022253797374656d000079310a3590e21100b8aef377c1aef3772040f577ac296642040000002d01010004000000f0010000040000002701ffff030000000000-максимальными подгруппами>
>3. Группы, в которых 010009000003a400000002001c0000000000030000001e000500000009020000000005000000020101000000050000000102ffffff00050000002e0118000000050000000c02a0014001050000000b02000000001200000026060f001a00ffffffff000010000000c0ffffffc6ffffff00010000660100000b00000026060f000c004d61746854797065000020001c000000fb0280fe0000000000009001000000cc0402001054696d6573204e657720526f6d616e00b8aef377c1aef3772040f57718286619040000002d01000008000000320a60013a000100000032010a00000026060f000a00ffffffff0100000000001c000000fb021000070000000000bc02000000cc0102022253797374656d0000d6440a3a90e21100b8aef377c1aef3772040f57718286619040000002d01010004000000f0010000040000002701ffff030000000000-максимальные подгруппы перестановочны с 010009000003a400000002001c0000000000030000001e000500000009020000000005000000020101000000050000000102ffffff00050000002e0118000000050000000c02c0012001050000000b02000000001200000026060f001a00ffffffff000010000000c0ffffffc6ffffffe0000000860100000b00000026060f000c004d61746854797065000030001c000000fb0280fe0000000000009001000000cc0402001054696d6573204e657720526f6d616e00b8aef377c1aef3772040f577c14466fe040000002d01000008000000320a60012e000100000033440a00000026060f000a00ffffffff0100000000001c000000fb021000070000000000bc02000000cc0102022253797374656d000018280a1b90e21100b8aef377c1aef3772040f577c14466fe040000002d01010004000000f0010000040000002701ffff030000000000-максимальными подгруппами>
>4. Группы, в которых максимальные подгруппы перестановочны с 010009000003a400000002001c0000000000030000001e000500000009020000000005000000020101000000050000000102ffffff00050000002e0118000000050000000c02c0012001050000000b02000000001200000026060f001a00ffffffff000010000000c0ffffffc6ffffffe0000000860100000b00000026060f000c004d61746854797065000030001c000000fb0280fe0000000000009001000000cc0402001054696d6573204e657720526f6d616e00b8aef377c1aef3772040f5772f33669c040000002d01000008000000320a60012e000100000033010a00000026060f000a00ffffffff0100000000001c000000fb021000070000000000bc02000000cc0102022253797374656d0000f6320a1490e21100b8aef377c1aef3772040f5772f33669c040000002d01010004000000f0010000040000002701ffff030000000000-максимальными подгруппами>
Заключение
Литература
Перечень условных обозначений
В
работе все рассматриваемые группы
предполагаются конечными. Используются
обозначения, принятые в книгах. Буквами
>
 >
обозначаются простые числа.
>
обозначаются простые числа.
Будем
различать знак включения множеств >
 >
и знак строгого включения >
>
и знак строгого включения >
 >;
>;
> >
и >
>
и >
 >
- соответственно знаки пересечения и
объединения множеств;
>
- соответственно знаки пересечения и
объединения множеств;
> >
-
пустое множество;
>
-
пустое множество;
> >
-
множество всех >
>
-
множество всех >
 >
для которых выполняется условие >
>
для которых выполняется условие >
 >;
>;
> >
-
множество всех натуральных чисел;
>
-
множество всех натуральных чисел;
> >
-
множество всех простых чисел;
>
-
множество всех простых чисел;
> >
-
некоторое множество простых чисел, т.е.
>
>
-
некоторое множество простых чисел, т.е.
>
 >;
>;
> >
-
дополнение к >
>
-
дополнение к >
 >
во множестве всех простых чисел; в
частности, >
>
во множестве всех простых чисел; в
частности, >
 >;
>;
примарное
число - любое число вида >
 >;
>;
Пусть
>
 >
- группа. Тогда:
>
- группа. Тогда:
> >
- порядок
группы >
>
- порядок
группы >
 >;
>;
> >
- порядок
элемента >
>
- порядок
элемента >
 >
группы >
>
группы >
 >;
>;
> >
- единичный
элемент и единичная подгруппа группы
>
>
- единичный
элемент и единичная подгруппа группы
>
 >;
>;
> >
- множество
всех простых делителей порядка группы
>
>
- множество
всех простых делителей порядка группы
>
 >;
>;
> >
- множество
всех различных простых делителей
натурального числа >
>
- множество
всех различных простых делителей
натурального числа >
 >;
>;
> >-группа
- группа >
>-группа
- группа >
 >,
для которой >
>,
для которой >
 >;
>;
> >-группа
- группа >
>-группа
- группа >
 >,
для которой >
>,
для которой >
 >;
>;
> >
- подгруппа
Фраттини группы >
>
- подгруппа
Фраттини группы >
 >,
т.е. пересечение всех максимальных
подгрупп группы >
>,
т.е. пересечение всех максимальных
подгрупп группы >
 >;
>;
> >
- подгруппа
Фиттинга группы >
>
- подгруппа
Фиттинга группы >
 >,
т.е. произведение всех нормальных
нильпотентных подгрупп группы >
>,
т.е. произведение всех нормальных
нильпотентных подгрупп группы >
 >;
>;
> >
- наибольшая
нормальная >
>
- наибольшая
нормальная >
 >-нильпотентная
подгруппа группы >
>-нильпотентная
подгруппа группы >
 >;
>;
> >
- коммутант
группы >
>
- коммутант
группы >
 >,
т.е. подгруппа, порожденная коммутаторами
всех элементов группы >
>,
т.е. подгруппа, порожденная коммутаторами
всех элементов группы >
 >;
>;
> >
- >
>
- >
 >-ый
коммутант группы >
>-ый
коммутант группы >
 >;
>;
> >
- наибольшая
нормальная >
>
- наибольшая
нормальная >
 >-подгруппа
группы >
>-подгруппа
группы >
 >;
>;
> >
- >
>
- >
 >-холловская
подгруппа группы >
>-холловская
подгруппа группы >
 >;
>;
> >
- силовская
>
>
- силовская
>
 >-подгруппа
группы >
>-подгруппа
группы >
 >;
>;
> >
- дополнение
к силовской >
>
- дополнение
к силовской >
 >-подгруппе
в группе >
>-подгруппе
в группе >
 >,
т.е. >
>,
т.е. >
 >-холловская
подгруппа группы >
>-холловская
подгруппа группы >
 >;
>;
> >
- группа всех
автоморфизмов группы >
>
- группа всех
автоморфизмов группы >
 >;
>;
> >
- >
>
- >
 >
является подгруппой группы >
>
является подгруппой группы >
 >;
>;
> >
- >
>
- >
 >
является собственной подгруппой группы
>
>
является собственной подгруппой группы
>
 >;
>;
> >
- >
>
- >
 >
является максимальной подгруппой группы
>
>
является максимальной подгруппой группы
>
 >;
>;
нетривиальная подгруппа - неединичная собственная подгруппа;
> >
- >
>
- >
 >
является нормальной подгруппой группы
>
>
является нормальной подгруппой группы
>
 >;
>;
> >
- подгруппа
>
>
- подгруппа
>
 >
характеристична в группе >
>
характеристична в группе >
 >,
т.е. >
>,
т.е. >
 >
для любого автоморфизма >
>
для любого автоморфизма >
 >;
>;
> >
- индекс
подгруппы >
>
- индекс
подгруппы >
 >
в группе >
>
в группе >
 >;
>;
> >;
>;
> >
- централизатор
подгруппы >
>
- централизатор
подгруппы >
 >
в группе >
>
в группе >
 >;
>;
> >
- нормализатор
подгруппы >
>
- нормализатор
подгруппы >
 >
в группе >
>
в группе >
 >;
>;
> >
- центр группы
>
>
- центр группы
>
 >;
>;
> >
- циклическая
группа порядка >
>
- циклическая
группа порядка >
 >;
>;
> >
- ядро подгруппы
>
>
- ядро подгруппы
>
 >
в группе >
>
в группе >
 >,
т.е. пересечение всех подгрупп, сопряжённых
с >
>,
т.е. пересечение всех подгрупп, сопряжённых
с >
 >
в >
>
в >
 >.
>.
Если >
 >
и >
>
и >
 >
- подгруппы группы >
>
- подгруппы группы >
 >,
то:
>,
то:
> >
- прямое
произведение подгрупп >
>
- прямое
произведение подгрупп >
 >
и >
>
и >
 >;
>;
> >
- полупрямое
произведение нормальной подгруппы >
>
- полупрямое
произведение нормальной подгруппы >
 >
и подгруппы >
>
и подгруппы >
 >;
>;
> >
- >
>
- >
 >
и >
>
и >
 >
изоморфны.
>
изоморфны.
Группа >
 >
называется:
>
называется:
примарной,
если >
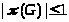 >;
>;
бипримарной,
если >
 >.
>.
Скобки >
 >
применяются для обозначения подгрупп,
порождённых некоторым множеством
элементов или подгрупп.
>
применяются для обозначения подгрупп,
порождённых некоторым множеством
элементов или подгрупп.
> >
- подгруппа,
порожденная всеми >
>
- подгруппа,
порожденная всеми >
 >,
для которых выполняется >
>,
для которых выполняется >
 >.
>.
> >,
где >
>,
где >
 >.
>.
Группу >
 >
называют:
>
называют:
> >-замкнутой,
если силовская >
>-замкнутой,
если силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >
нормальна в >
>
нормальна в >
 >;
>;
> >-нильпотентной,
если >
>-нильпотентной,
если >
 >-холловская
подгруппа группы >
>-холловская
подгруппа группы >
 >
нормальна в >
>
нормальна в >
 >;
>;
> >-разрешимой,
если существует нормальный ряд, факторы
которого либо >
>-разрешимой,
если существует нормальный ряд, факторы
которого либо >
 >-группы,
либо >
>-группы,
либо >
 >-группы;
>-группы;
> >-сверхразрешимой,
если каждый ее главный фактор является
либо >
>-сверхразрешимой,
если каждый ее главный фактор является
либо >
 >-группой,
либо циклической группой;
>-группой,
либо циклической группой;
нильпотентной, если все ее силовские подгруппы нормальны;
метанильпотентной,
если существует нормальная нильпотентная
подгруппа >
 >
группы >
>
группы >
 >
такая, что >
>
такая, что >
 >
нильпотентна.
>
нильпотентна.
разрешимой,
если существует номер >
 >
такой, что >
>
такой, что >
 >;
>;
сверхразрешимой, если она обладает главным рядом, все индексы которого являются простыми числами.
Группа Шмидта - это конечная ненильпотентная группа, все собственные группы которой нильпотентны.
Добавлением
к подгруппе >
 >
группы >
>
группы >
 >
называется такая подгруппа >
>
называется такая подгруппа >
 >
из >
>
из >
 >,
что >
>,
что >
 >.
>.
Минимальная
нормальная подгруппа группы >
 >
- неединичная нормальная подгруппа
группы >
>
- неединичная нормальная подгруппа
группы >
 >,
не содержащая собственных неединичных
нормальных подгрупп группы >
>,
не содержащая собственных неединичных
нормальных подгрупп группы >
 >.
>.
Цоколь группы
>
 >
- произведение всех минимальных нормальных
подгрупп группы >
>
- произведение всех минимальных нормальных
подгрупп группы >
 >.
>.
> >
- цоколь
группы >
>
- цоколь
группы >
 >.
>.
Экспонента
группы >
 >
- это наименьшее общее кратное порядков
всех ее элементов.
>
- это наименьшее общее кратное порядков
всех ее элементов.
Цепь - это совокупность вложенных друг в друга подгрупп. Ряд подгрупп - это цепь, состоящая из конечного числа членов и проходящая через единицу.
Ряд подгрупп
>
 >
называется:
>
называется:
субнормальным,
если >
 >
для любого >
>
для любого >
 >;
>;
нормальным,
если >
 >
для любого >
>
для любого >
 >;
>;
главным, если
>
 >
является минимальной нормальной
подгруппой в >
>
является минимальной нормальной
подгруппой в >
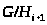 >
для всех >
>
для всех >
 >.
>.
Классы групп, т.е. совокупности групп, замкнутые относительно изоморфизмов, обозначаются прописными готическими буквами. Также обозначаются формации, т.е. классы групп, замкнутые относительно факторгрупп и подпрямых произведений. За некоторыми классами закреплены стандартные обозначения:
> >
- класс всех
групп;
>
- класс всех
групп;
> >
- класс всех
абелевых групп;
>
- класс всех
абелевых групп;
> >
- класс всех
нильпотентных групп;
>
- класс всех
нильпотентных групп;
> >
- класс всех
разрешимых групп;
>
- класс всех
разрешимых групп;
> >
- класс всех
>
>
- класс всех
>
 >-групп;
>-групп;
> >
- класс всех
сверхразрешимых групп;
>
- класс всех
сверхразрешимых групп;
> >
- класс всех
абелевых групп экспоненты, делящей >
>
- класс всех
абелевых групп экспоненты, делящей >
 >.
>.
Формации - это классы конечных групп, замкнутые относительно взятия гомоморфных образов и конечных подпрямых произведений.
Пусть >
 >
- некоторый класс групп и >
>
- некоторый класс групп и >
 >
- группа, тогда:
>
- группа, тогда:
> >
- >
>
- >
 >-корадикал
группы >
>-корадикал
группы >
 >,
т.е. пересечение всех тех нормальных
подгрупп >
>,
т.е. пересечение всех тех нормальных
подгрупп >
 >
из >
>
из >
 >,
для которых >
>,
для которых >
 >.
Если >
>.
Если >
 >
- формация, то >
>
- формация, то >
 >
является наименьшей нормальной подгруппой
группы >
>
является наименьшей нормальной подгруппой
группы >
 >,
факторгруппа по которой принадлежит
>
>,
факторгруппа по которой принадлежит
>
 >.
Если >
>.
Если >
 >
- формация всех сверхразрешимых групп,
то >
>
- формация всех сверхразрешимых групп,
то >
 >
называется сверхразрешимым корадикалом
группы >
>
называется сверхразрешимым корадикалом
группы >
 >.
>.
Формация >
 >
называется насыщенной, если всегда из
>
>
называется насыщенной, если всегда из
>
 >
следует, что и >
>
следует, что и >
 >.
>.
Класс групп
>
 >
называется наследственным или замкнутым
относительно подгрупп, если из того,
что >
>
называется наследственным или замкнутым
относительно подгрупп, если из того,
что >
 >
следует, что и каждая подгруппа группы
>
>
следует, что и каждая подгруппа группы
>
 >
также принадлежит >
>
также принадлежит >
 >.
>.
Произведение
формаций >
 >
и >
>
и >
 >
состоит из всех групп >
>
состоит из всех групп >
 >,
для которых >
>,
для которых >
 >,
т.е. >
>,
т.е. >
 >.
>.
Пусть >
 >
- некоторая непустая формация. Максимальная
подгруппа >
>
- некоторая непустая формация. Максимальная
подгруппа >
 >
группы >
>
группы >
 >
называется >
>
называется >
 >-абнормальной,
если >
>-абнормальной,
если >
 >.
>.
Подгруппы >
 >
и >
>
и >
 >
группы >
>
группы >
 >
называются перестановочными, если >
>
называются перестановочными, если >
 >.
>.
Пусть >
 >,
>
>,
>
 >
-подгруппы группы >
>
-подгруппы группы >
 >
и >
>
и >
 >.
Тогда >
>.
Тогда >
 >
называется:
>
называется:
(1)
>
 >-перестановочной
с >
>-перестановочной
с >
 >,
если в >
>,
если в >
 >
имеется такой элемент >
>
имеется такой элемент >
 >,
что >
>,
что >
 >;
>;
(2) наследственно
>
 >-перестановочной
с >
>-перестановочной
с >
 >,
если в >
>,
если в >
 >
имеется такой элемент >
>
имеется такой элемент >
 >,
что >
>,
что >
 >.
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Нормальным индексом подгруппы >
>.
Нормальным индексом подгруппы >
 >
называют порядок главного фактора >
>
называют порядок главного фактора >
 >,
где >
>,
где >
 >
и >
>
и >
 >,
и обозначают символом >
>,
и обозначают символом >
 >.
>.
Подгруппа >
 >
группы >
>
группы >
 >
называется >
>
называется >
 >-максимальной
подгруппой или иначе второй максимальной
подгруппой в >
>-максимальной
подгруппой или иначе второй максимальной
подгруппой в >
 >,
если в >
>,
если в >
 >
найдется такая максимальная подгруппа
>
>
найдется такая максимальная подгруппа
>
 >,
в которой >
>,
в которой >
 >
является максимальной подгруппой.
Аналогично определяют >
>
является максимальной подгруппой.
Аналогично определяют >
 >-максимальные
(третьи максимальные) подгруппы,
>
>-максимальные
(третьи максимальные) подгруппы,
>
 >-максимальные
подгруппы и т.д.
>-максимальные
подгруппы и т.д.
Введение
Подгруппы >
 >
и >
>
и >
 >
группы >
>
группы >
 >
называются перестановочными, если >
>
называются перестановочными, если >
 >.
Подгруппа >
>.
Подгруппа >
 >
группы >
>
группы >
 >
называется перестановочной или
квазинормальной в >
>
называется перестановочной или
квазинормальной в >
 >,
если >
>,
если >
 >
перестановочна с каждой подгруппой
группы >
>
перестановочна с каждой подгруппой
группы >
 >.
>.
Перестановочные
подгруппы обладают рядом интересных
свойств, чем был и вызван широкий интерес
к анализу перестановочных и частично
перестановочных подгрупп в целом.
Изучение перестановочных подгрупп было
начато в классической работе Оре, где
было доказано, что любая перестановочная
подгруппа является субнормальной.
Подгруппы, перестановочные с силовскими
подгруппами, впервые изучались в работе
С.А. Чунихина . Отметим, что подгруппы
такого типа были названы позднее в
работе Кегеля >
 >-квазинормальными.
В 60-70-х годах прошлого столетия появились
ряд ключевых работ по теории перестановочных
подгрупп, которые предопределили
основные направления развития теории
перестановочных подгрупп в последующие
годы. Уточняя отмеченный выше результат
Оре, Ито и Сеп в работе доказали, что для
каждой перестановочной подгруппы >
>-квазинормальными.
В 60-70-х годах прошлого столетия появились
ряд ключевых работ по теории перестановочных
подгрупп, которые предопределили
основные направления развития теории
перестановочных подгрупп в последующие
годы. Уточняя отмеченный выше результат
Оре, Ито и Сеп в работе доказали, что для
каждой перестановочной подгруппы >
 >
группы >
>
группы >
 >
факторгруппа >
>
факторгруппа >
 >
нильпотентна. В другом направлении этот
результат Оре получил развитие в работах
Кегеля и Дескинса. Кегель доказал, что
любая >
>
нильпотентна. В другом направлении этот
результат Оре получил развитие в работах
Кегеля и Дескинса. Кегель доказал, что
любая >
 >-квазинормальная
подгруппа является субнормальной и
показал, что подгруппы, перестановочные
с силовскими подгруппами, образуют
решетку. Первый из этих двух результатов
Дескинс обобщил следующим образом, если
>
>-квазинормальная
подгруппа является субнормальной и
показал, что подгруппы, перестановочные
с силовскими подгруппами, образуют
решетку. Первый из этих двух результатов
Дескинс обобщил следующим образом, если
>
 >
порождается своими >
>
порождается своими >
 >-элементами
и >
>-элементами
и >
 >-подгруппа
>
>-подгруппа
>
 >
группы >
>
группы >
 >
>
>
>
 >-квазинормальна
в >
>-квазинормальна
в >
 >,
то факторгруппа >
>,
то факторгруппа >
 >
нильпотентна. В этой работе Дескинс
высказал предположение о том, что для
квазинормальной в >
>
нильпотентна. В этой работе Дескинс
высказал предположение о том, что для
квазинормальной в >
 >
подгруппы >
>
подгруппы >
 >
факторгруппа >
>
факторгруппа >
 >
абелева. Отрицательное решение этой
задачи было получено Томпсоном в работе.
>
абелева. Отрицательное решение этой
задачи было получено Томпсоном в работе.
Отметим, что
после выхода работ, частично перестановочные
подгруппы стали активно использоваться
в исследованиях многих авторов. В
частности, в работе Э.М. Пальчик исследовал
свойства >
 >-квазинормальных
подгрупп, т. е. подгрупп перестановочных
со всеми бипримарными подгруппами
группы >
>-квазинормальных
подгрупп, т. е. подгрупп перестановочных
со всеми бипримарными подгруппами
группы >
 >.
Существенно усиливая результат работы,
Майер и Шмид доказали, что если >
>.
Существенно усиливая результат работы,
Майер и Шмид доказали, что если >
 >
- квазинормальная подгруппа конечной
группы >
>
- квазинормальная подгруппа конечной
группы >
 >,
то факторгруппа >
>,
то факторгруппа >
 >
содержится в гиперцентре факторгруппы
>
>
содержится в гиперцентре факторгруппы
>
 >,
где >
>,
где >
 >
- ядро подгруппы >
>
- ядро подгруппы >
 >.
Отметим, что аналогичный результат для
подгрупп, перестановочных с силовскими
подгруппами, был получен лишь в недавней
работе П. Шмидта. Стоунхьюер в работе
обобщил результат Оре на случай
бесконечных групп. Он доказал, что каждая
перестановочная подгруппа конечно
порожденной группы субнормальна.
>.
Отметим, что аналогичный результат для
подгрупп, перестановочных с силовскими
подгруппами, был получен лишь в недавней
работе П. Шмидта. Стоунхьюер в работе
обобщил результат Оре на случай
бесконечных групп. Он доказал, что каждая
перестановочная подгруппа конечно
порожденной группы субнормальна.
Значительные
успехи, достигнутые в изучении
перестановочных подгрупп, в 1960-1980 годах
послужили основой для дальнейшего
изучения групп по наличию в них тех или
иных систем перестановочных подгрупп.
В частности, Хупперт доказал, что
разрешимая группа >
 >
сверхразрешима, если все максимальные
подгруппы всех силовских подгрупп из
>
>
сверхразрешима, если все максимальные
подгруппы всех силовских подгрупп из
>
 >
перестановочны с силовскими подгруппами
из >
>
перестановочны с силовскими подгруппами
из >
 >,
и группа >
>,
и группа >
 >
разрешима, если в ней имеется такая
силовская подгруппа >
>
разрешима, если в ней имеется такая
силовская подгруппа >
 >
и такое ее дополнение >
>
и такое ее дополнение >
 >,
что >
>,
что >
 >
перестановочна со всеми максимальными
подгруппами из >
>
перестановочна со всеми максимальными
подгруппами из >
 >.
Эти два результата Хупперта дали толчок
большому числу публикаций, cвязанных с
исследованием влияния на строение
основой группы максимальных подгрупп
силовских подгрупп и, в частности, с
исследованием перестановочности таких
подгрупп. Другой результат, давший
значительный импульс к исследованию
групп с заданными системами перестановочных
подгрупп был получен Асаадом и Шаланом
в их совместной работе, где была доказана
сверхразрешимость конечной группы >
>.
Эти два результата Хупперта дали толчок
большому числу публикаций, cвязанных с
исследованием влияния на строение
основой группы максимальных подгрупп
силовских подгрупп и, в частности, с
исследованием перестановочности таких
подгрупп. Другой результат, давший
значительный импульс к исследованию
групп с заданными системами перестановочных
подгрупп был получен Асаадом и Шаланом
в их совместной работе, где была доказана
сверхразрешимость конечной группы >
 >
при условии, что >
>
при условии, что >
 >,
где все подгруппы из >
>,
где все подгруппы из >
 >
перестановочны со всеми подгруппами
из >
>
перестановочны со всеми подгруппами
из >
 >.
Идеи этой работы и, в частности, отмеченный
здесь результат этой работы были развиты
во многих направлениях в исследованиях
многих авторов, где на основе
перестановочности были описаны многие
важные классы конечных и бесконечных
групп .
>.
Идеи этой работы и, в частности, отмеченный
здесь результат этой работы были развиты
во многих направлениях в исследованиях
многих авторов, где на основе
перестановочности были описаны многие
важные классы конечных и бесконечных
групп .
В работе Го
Вэньбиня, Шама и А.Н. Скибы было рассмотрено
новое обобщение понятия перестановочной
подгруппы. Согласно, погруппы >
 >
и >
>
и >
 >
называются >
>
называются >
 >-перестановочными,
где >
>-перестановочными,
где >
 >,
если в >
>,
если в >
 >
имеется такой элемент >
>
имеется такой элемент >
 >,
что >
>,
что >
 >.
Используя понятие >
>.
Используя понятие >
 >-перестановочности
можно охарактеризовать многие важные
классы групп по наличию в них тех или
иных >
>-перестановочности
можно охарактеризовать многие важные
классы групп по наличию в них тех или
иных >
 >-перестановочных
подгрупп для подходящих >
>-перестановочных
подгрупп для подходящих >
 >.
Согласно, группа >
>.
Согласно, группа >
 >
является сверхразрешимой тогда и только
тогда, когда все ее максимальные подгруппы
>
>
является сверхразрешимой тогда и только
тогда, когда все ее максимальные подгруппы
>
 >-перестановочны
со всеми другими подгруппами этой
группы. Новые характеризации в терминах
>
>-перестановочны
со всеми другими подгруппами этой
группы. Новые характеризации в терминах
>
 >-перестановочных
подгрупп для класов разрешимых,
сверхразрешимых и нильпотентных групп
можно найти в работах.
>-перестановочных
подгрупп для класов разрешимых,
сверхразрешимых и нильпотентных групп
можно найти в работах.
Таким образом, задача изучения групп с заданной системой перестановочных и обобщенно перестановочных подгрупп вполне актуальна, и дальнейшей ее реализации посвящена данная работа.
1. Классификация групп с перестановочными обобщенно максимальными подгруппами
Результаты,
связанные с изучением максимальных
подгрупп, составили одно из самых
содержательных направлений в теории
конечных групп. Это связано прежде всего
с тем, что многие известные классы групп
допускают описания на основе свойств
максимальных подгрупп. Отметим, например,
что группа >
 >
нильпотентна тогда и только тогда, когда
все ее максимальные подгруппы нормальны;
сверхразрешима тогда и только тогда,
когда индексы всех ее максимальных
подгрупп просты ; разрешима тогда и
только тогда, когда у любой ее максимальной
подгруппы нормальный индекс совпадает
с обычным индексом . Отметим также, что
максимальные подгруппы лежат в основе
многих важных признаков принадлежности
группы выделенному классу групп. Наиболее
известными результатами в этом направлении
являются теорема Дескинса-Томпсона-Янко
о том, что группа разрешима, если она
обладает максимальной нильпотентной
подгруппой, у которой класс нильпотентности
силовских >
>
нильпотентна тогда и только тогда, когда
все ее максимальные подгруппы нормальны;
сверхразрешима тогда и только тогда,
когда индексы всех ее максимальных
подгрупп просты ; разрешима тогда и
только тогда, когда у любой ее максимальной
подгруппы нормальный индекс совпадает
с обычным индексом . Отметим также, что
максимальные подгруппы лежат в основе
многих важных признаков принадлежности
группы выделенному классу групп. Наиболее
известными результатами в этом направлении
являются теорема Дескинса-Томпсона-Янко
о том, что группа разрешима, если она
обладает максимальной нильпотентной
подгруппой, у которой класс нильпотентности
силовских >
 >-подгрупп
не превосходит 2 и теорема О.Ю. Шмидта о
разрешимости группы, у которой все
максимальные подгруппы нильпотентны.
Отметим, что разрешимость групп, у
которых все максимальные подгруппы
сверхразрешимы, была установлена
Хуппертом.
>-подгрупп
не превосходит 2 и теорема О.Ю. Шмидта о
разрешимости группы, у которой все
максимальные подгруппы нильпотентны.
Отметим, что разрешимость групп, у
которых все максимальные подгруппы
сверхразрешимы, была установлена
Хуппертом.
По мере
развития теории максимальных подгрупп
многими авторами предпринимались также
попытки изучения и применения
>
 >-максимальных,
>
>-максимальных,
>
 >-максимальных
и т.д. подгрупп. При этом, как и для
максимальных подгрупп, с одной стороны
рассматривались группы с различными
ограничениями на способ вложения
обобщенно максимальных подгрупп в эти
группы, с другой стороны исследовались
свойства основной группы в зависимости
от условий, накладываемых на внутреннее
строение >
>-максимальных
и т.д. подгрупп. При этом, как и для
максимальных подгрупп, с одной стороны
рассматривались группы с различными
ограничениями на способ вложения
обобщенно максимальных подгрупп в эти
группы, с другой стороны исследовались
свойства основной группы в зависимости
от условий, накладываемых на внутреннее
строение >
 >-максимальных,
>
>-максимальных,
>
 >-максимальных
и т.д. подгрупп. Пожалуй, наиболее ранний
результат, относящийся к этому направлению,
был получен Хуппертом, установившим
сверхразрешимость группы, у которой
все вторые максимальные подгруппы
нормальны. В дальнейшем этот результат
был развит в нескольких направлениях.
В частности, сверхразрешимость разрешимых
групп, у которых все вторые максимальные
подгруппы перестановочны со всеми
силовскими подгруппами было установлена
Агровалем , а в работе Л.А. Поляков
доказал, что группа сверхразрешима,
если любая ее >
>-максимальных
и т.д. подгрупп. Пожалуй, наиболее ранний
результат, относящийся к этому направлению,
был получен Хуппертом, установившим
сверхразрешимость группы, у которой
все вторые максимальные подгруппы
нормальны. В дальнейшем этот результат
был развит в нескольких направлениях.
В частности, сверхразрешимость разрешимых
групп, у которых все вторые максимальные
подгруппы перестановочны со всеми
силовскими подгруппами было установлена
Агровалем , а в работе Л.А. Поляков
доказал, что группа сверхразрешима,
если любая ее >
 >-максимальная
подгруппа перестановочна со всеми
максимальными подгруппами этой группы
.
>-максимальная
подгруппа перестановочна со всеми
максимальными подгруппами этой группы
.
Оказалось,
что группы, у которых все >
 >-максимальные
подгруппы нильпотентны, не обязательно
разрешимы и полное описание групп с
таким свойством в неразрешимом случае
было получено Янком, а в разрешимом
случае В.А. Белоноговым. Группы, у которых
все >
>-максимальные
подгруппы нильпотентны, не обязательно
разрешимы и полное описание групп с
таким свойством в неразрешимом случае
было получено Янком, а в разрешимом
случае В.А. Белоноговым. Группы, у которых
все >
 >-максимальные
подгруппы абелевы, были описаны Я.Г.
Берковичем в работе. Эти результаты
получили развитие в работе В.Н. Семенчука,
который дал полное описание разрешимых
групп, у которых все их >
>-максимальные
подгруппы абелевы, были описаны Я.Г.
Берковичем в работе. Эти результаты
получили развитие в работе В.Н. Семенчука,
который дал полное описание разрешимых
групп, у которых все их >
 >-максимальные
подгруппы сверхразрешимы.
>-максимальные
подгруппы сверхразрешимы.
В последние
годы получен ряд новых интересных
результатов о >
 >-максимальных
подгруппах, связанных с изучением их
способа вложения в основную группу. В
этой связи, прежде всего , в которых на
языке >
>-максимальных
подгруппах, связанных с изучением их
способа вложения в основную группу. В
этой связи, прежде всего , в которых на
языке >
 >-максимальных
подгрупп получены описания ряда важных
классов групп. Напомним, что подгруппа
>
>-максимальных
подгрупп получены описания ряда важных
классов групп. Напомним, что подгруппа
>
 >
группы >
>
группы >
 >
обладает свойством покрытия-изолирования,
если для любого главного фактора >
>
обладает свойством покрытия-изолирования,
если для любого главного фактора >
 >
группы >
>
группы >
 >
выполняется одно из двух условий >
>
выполняется одно из двух условий >
 >
или >
>
или >
 >.
В работе доказано, что группа >
>.
В работе доказано, что группа >
 >
разрешима тогда и только тогда, когда
в >
>
разрешима тогда и только тогда, когда
в >
 >
имеется такая >
>
имеется такая >
 >-максимальная
разрешимая подгруппа, которая обладает
свойством покрытия-изолирования. Отметим
также, что в работе, а также в работе
изучалось строение групп, в зависимоси
от >
>-максимальная
разрешимая подгруппа, которая обладает
свойством покрытия-изолирования. Отметим
также, что в работе, а также в работе
изучалось строение групп, в зависимоси
от >
 >-максимальных
подгрупп их силовских подгрупп.
>-максимальных
подгрупп их силовских подгрупп.
Пусть >
 >
и >
>
и >
 >
- подгруппы группы >
>
- подгруппы группы >
 >.
Тогда подгруппа >
>.
Тогда подгруппа >
 >
называется >
>
называется >
 >-перестановочной
с >
>-перестановочной
с >
 >,
если в >
>,
если в >
 >
найдется такой элемент >
>
найдется такой элемент >
 >,
что >
>,
что >
 >.
В работе найдены новые описания
нильпотентных и сверхразрешимых групп
на основе условия >
>.
В работе найдены новые описания
нильпотентных и сверхразрешимых групп
на основе условия >
 >
-перестановочности для >
>
-перестановочности для >
 >-максимальных
подгрупп. В частности, доказано, что:
Группа >
>-максимальных
подгрупп. В частности, доказано, что:
Группа >
 >
нильпотентна тогда и только тогда, когда
для любой >
>
нильпотентна тогда и только тогда, когда
для любой >
 >-максимальной
подгруппы >
>-максимальной
подгруппы >
 >
группы >
>
группы >
 >,
имеющей непримарный индекс, в >
>,
имеющей непримарный индекс, в >
 >
найдется такая нильпотентная подгруппа
>
>
найдется такая нильпотентная подгруппа
>
 >,
что >
>,
что >
 >
и >
>
и >
 >
>
>
>
 >-перестановочна
со всеми подгруппами из >
>-перестановочна
со всеми подгруппами из >
 >.
>.
Пусть >
 >
- набор всех >
>
- набор всех >
 >-максимальных
подгрупп группы >
>-максимальных
подгрупп группы >
 >.
>.
Как показывают
упомянутые выше результаты работ,
условия перестановочности, накладываемые
на подгруппы из >
 >,
существенно определяют строение основной
группы. В работе Л.Я. Полякова было
доказано, что группа >
>,
существенно определяют строение основной
группы. В работе Л.Я. Полякова было
доказано, что группа >
 >
разрешима, если любая подгруппа из >
>
разрешима, если любая подгруппа из >
 >
перестановочна со всеми подгруппами
из >
>
перестановочна со всеми подгруппами
из >
 >
для всех >
>
для всех >
 >,
где >
>,
где >
 >.
В связи с этим результатом естественно
возникает вопрос о полном описании
групп с таким свойством. Решению данной
задачи и посвящена настоящая глава.
>.
В связи с этим результатом естественно
возникает вопрос о полном описании
групп с таким свойством. Решению данной
задачи и посвящена настоящая глава.
2.
Группы с >
 >-перестановочными
>
>-перестановочными
>
 >-максимальными
подгруппами
>-максимальными
подгруппами
Отмеченные выше результаты работы допускают следующие уточнения.
[2.1]. Пусть
>
 >
- группа, >
>
- группа, >
 >
- ее подгруппа Фиттинга. Если любая
>
>
- ее подгруппа Фиттинга. Если любая
>
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
>
>
>
 >-перестановочна
со всеми максимальными подгруппами
группы >
>-перестановочна
со всеми максимальными подгруппами
группы >
 >,
то группа >
>,
то группа >
 >
метанильпотентна.
>
метанильпотентна.
Доказательство.
Предположим, что теорема не верна, и
пусть >
 >
- контрпример минимального порядка.
Доказательство разобьем на следующие
этапы.
>
- контрпример минимального порядка.
Доказательство разобьем на следующие
этапы.
(1) Для любой
неединичной нормальной в >
 >
подгруппы >
>
подгруппы >
 >
факторгруппа >
>
факторгруппа >
 >
метанильпотентна.
>
метанильпотентна.
Рассмотрим
факторгруппу >
 >.
Пусть >
>.
Пусть >
 >
- произвольная максимальная в >
>
- произвольная максимальная в >
 >
подгруппа и >
>
подгруппа и >
 >
- произвольная >
>
- произвольная >
 >-максимальная
>
>-максимальная
>
 >
подгруппа. Тогда >
>
подгруппа. Тогда >
 >
максимальна в >
>
максимальна в >
 >
и >
>
и >
 >
>
>
>
 >-максимальна
в >
>-максимальна
в >
 >,
а значит, по условию подгруппа >
>,
а значит, по условию подгруппа >
 >
>
>
>
 >-перестановочна
с подгруппой >
>-перестановочна
с подгруппой >
 >.
Но тогда, согласно лемме Error: Reference source not found,
подгруппа >
>.
Но тогда, согласно лемме Error: Reference source not found,
подгруппа >
 >
>
>
>
 >-перестановочна
с подгруппой >
>-перестановочна
с подгруппой >
 >.
Итак, условие теоремы выполняется в >
>.
Итак, условие теоремы выполняется в >
 >.
Но >
>.
Но >
 >
и поэтому согласно выбора группы >
>
и поэтому согласно выбора группы >
 >,
мы имеем (1).
>,
мы имеем (1).
(2) >
 >
- разрешимая группа.
>
- разрешимая группа.
Если в группе
>
 >
существует единичная >
>
существует единичная >
 >-максимальная
подгруппа, то теорема очевидно справедлива.
Предположим, что в группе >
>-максимальная
подгруппа, то теорема очевидно справедлива.
Предположим, что в группе >
 >
все >
>
все >
 >-максимальные
подгруппы отличны от единицы. Докажем,
что для каждой максимальной подгруппы
>
>-максимальные
подгруппы отличны от единицы. Докажем,
что для каждой максимальной подгруппы
>
 >
группы >
>
группы >
 >,
>
>,
>
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Тогда по условию для каждого >
>.
Тогда по условию для каждого >
 >,
мы имеем >
>,
мы имеем >
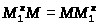 >.
Ввиду леммы Error: Reference source not found, >
>.
Ввиду леммы Error: Reference source not found, >
 >
и, следовательно, >
>
и, следовательно, >
 >.
Значит, >
>.
Значит, >
 >.
Поскольку >
>.
Поскольку >
 >,
то >
>,
то >
 >
и поэтому по выбору группы >
>
и поэтому по выбору группы >
 >
мы заключаем, что >
>
мы заключаем, что >
 >
- разрешимая группа. Это означает, что
>
>
- разрешимая группа. Это означает, что
>
 >
разрешима, и следовательно, >
>
разрешима, и следовательно, >
 >
- разрешимая группа.
>
- разрешимая группа.
(3) Группа
>
 >
имеет единственную минимальную нормальную
подгруппу >
>
имеет единственную минимальную нормальную
подгруппу >
 >
и >
>
и >
 >,
где >
>,
где >
 >
и >
>
и >
 >
- максимальная в >
>
- максимальная в >
 >
подгруппа, которая не является
нильпотентной группой.
>
подгруппа, которая не является
нильпотентной группой.
Пусть >
 >
- произвольная минимальная нормальная
подгруппа группы >
>
- произвольная минимальная нормальная
подгруппа группы >
 >.
Так как класс всех метанильпотентных
групп образует насыщенную формацию
(см. лемму Error: Reference source not found), то >
>.
Так как класс всех метанильпотентных
групп образует насыщенную формацию
(см. лемму Error: Reference source not found), то >
 >
- единственная минимальная нормальная
подгруппа в >
>
- единственная минимальная нормальная
подгруппа в >
 >,
причем >
>,
причем >
 >.
В силу (2), >
>.
В силу (2), >
 >
является элементарной абелевой >
>
является элементарной абелевой >
 >-группой
для некоторого простого >
>-группой
для некоторого простого >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >
такая, что >
>
такая, что >
 >.
Пусть >
>.
Пусть >
 >.
Ясно, что >
>.
Ясно, что >
 >.
Так как >
>.
Так как >
 >,
мы видим, что >
>,
мы видим, что >
 >.
Это показывает, что >
>.
Это показывает, что >
 >
и, следовательно, >
>
и, следовательно, >
 >.
Ясно, что >
>.
Ясно, что >
 >
и поэтому по выбору группы >
>
и поэтому по выбору группы >
 >,
>
>,
>
 >
не является нильпотентной группой.
>
не является нильпотентной группой.
(4) Заключительное противоречие.
В силу (3), в
группе >
 >
имеется максимальная подгруппа >
>
имеется максимальная подгруппа >
 >,
которая не является нормальной подгруппой
в >
>,
которая не является нормальной подгруппой
в >
 >.
Поскольку для любого >
>.
Поскольку для любого >
 >,
>
>,
>
 >
- максимальная в >
>
- максимальная в >
 >
подгруппа и >
>
подгруппа и >
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >,
то >
>,
то >
 >
- >
>
- >
 >-максимальная
в >
>-максимальная
в >
 >
подгруппа. Если >
>
подгруппа. Если >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >,
то >
>,
то >
 >.
Значит, >
>.
Значит, >
 >
не является нормальной подгруппой в >
>
не является нормальной подгруппой в >
 >.
Покажем, что >
>.
Покажем, что >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Пусть >
>.
Пусть >
 >.
Пусть >
>.
Пусть >
 >
- такая максимальная подгруппа группы
>
>
- такая максимальная подгруппа группы
>
 >,
что >
>,
что >
 >.
Тогда >
>.
Тогда >
 >.
Значит, >
>.
Значит, >
 >
или >
>
или >
 >.
Первый случай, очевидно, невозможен.
Следовательно, >
>.
Первый случай, очевидно, невозможен.
Следовательно, >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- максимальная в >
>
- максимальная в >
 >
подгруппа. Тогда для любого >
>
подгруппа. Тогда для любого >
 >,
>
>,
>
 >
>
>
>
 >-перестановочна
с >
>-перестановочна
с >
 >.
Поскольку >
>.
Поскольку >
 >,
то ввиду леммы Error: Reference source not found(6), >
>,
то ввиду леммы Error: Reference source not found(6), >
 >
перестановочна с >
>
перестановочна с >
 >.
Из максимальности подгруппы >
>.
Из максимальности подгруппы >
 >
следует, что >
>
следует, что >
 >
или >
>
или >
 >.
Если >
>.
Если >
 >,
то ввиду леммы Error: Reference source not found, >
>,
то ввиду леммы Error: Reference source not found, >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >.
Тогда >
>.
Тогда >
 >
для любого >
>
для любого >
 >
и поэтому >
>
и поэтому >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Это означает, что >
>.
Это означает, что >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >,
противоречие. Теорема доказана.
>,
противоречие. Теорема доказана.
[2.1]. Каждая
>
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
перестановочна с любой максимальной
подгруппой в >
>
перестановочна с любой максимальной
подгруппой в >
 >
тогда и только тогда, когда либо >
>
тогда и только тогда, когда либо >
 >
нильпотентна, либо >
>
нильпотентна, либо >
 >
- такая ненильпотентная группа с >
>
- такая ненильпотентная группа с >
 >,
что циклическая силовская >
>,
что циклическая силовская >
 >-подгруппа
>
>-подгруппа
>
 >
группы >
>
группы >
 >
не нормальна в >
>
не нормальна в >
 >,
а максимальная подгруппа группы >
>,
а максимальная подгруппа группы >
 >
нормальна в >
>
нормальна в >
 >.
>.
Доказательство.
Необходимость. Разрешимость группы >
 >
следует из теоремы Error: Reference source not found.
Предположим теперь, что >
>
следует из теоремы Error: Reference source not found.
Предположим теперь, что >
 >
не является нильпотентной группой.
Пусть >
>
не является нильпотентной группой.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
которая не является нормальной в >
>,
которая не является нормальной в >
 >.
Пусть >
>.
Пусть >
 >
и >
>
и >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Рассуждая как выше видим, что >
>.
Рассуждая как выше видим, что >
 >.
Следовательно, >
>.
Следовательно, >
 >,
и >
>,
и >
 >
- циклическая примарная группа. Пусть
>
>
- циклическая примарная группа. Пусть
>
 >.
Покажем, что >
>.
Покажем, что >
 >.
Допустим, что >
>.
Допустим, что >
 >.
Пусть >
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >
и >
>
и >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Тогда >
>.
Тогда >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
и, следовательно, по условию >
>
и, следовательно, по условию >
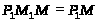 >
- подгруппа группы >
>
- подгруппа группы >
 >,
что противоречит максимальности
подгруппы >
>,
что противоречит максимальности
подгруппы >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >.
>.
Достаточность очевидна. Следствие доказано.
[2.2]. Если в
группе >
 >
любая ее максимальная подгруппа
перестановочна со всеми >
>
любая ее максимальная подгруппа
перестановочна со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >
и >
>
и >
 >,
то >
>,
то >
 >
- нильпотентная группа.
>
- нильпотентная группа.
В дальнейшем нам потребуется следующая теорема.
[2.2]. Пусть
>
 >
- группа, >
>
- группа, >
 >
- ее подгруппа Фиттинга. Если любая
>
>
- ее подгруппа Фиттинга. Если любая
>
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
>
>
>
 >-перестановочна
со всеми >
>-перестановочна
со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >,
то группа >
>,
то группа >
 >
разрешима и >
>
разрешима и >
 >
для каждого простого >
>
для каждого простого >
 >.
>.
Доказательство.
Предположим, что данная теорема не
верна, и пусть >
 >
- контрпример минимального порядка.
Доказательство разобьем на следующие
этапы.
>
- контрпример минимального порядка.
Доказательство разобьем на следующие
этапы.
(1) >
 >
- разрешимая группа.
>
- разрешимая группа.
Действительно,
если >
 >,
то каждая >
>,
то каждая >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
перестановочна со всеми 3-максимальными
подгруппами группы >
>
перестановочна со всеми 3-максимальными
подгруппами группы >
 >.
Тогда по следствию Error: Reference source not found,
каждая максимальная подгруппа группы
>
>.
Тогда по следствию Error: Reference source not found,
каждая максимальная подгруппа группы
>
 >
сверхразрешима. Согласно известной
теоремы Хупперта Error: Reference source not found о
разрешимости группы, в которой все
собственные подгруппы сверхразрешимы,
>
>
сверхразрешима. Согласно известной
теоремы Хупперта Error: Reference source not found о
разрешимости группы, в которой все
собственные подгруппы сверхразрешимы,
>
 >
- разрешимая группа.
>
- разрешимая группа.
Пусть теперь
>
 >.
Так как условие теоремы справедливо
для группы >
>.
Так как условие теоремы справедливо
для группы >
 >,
то группа >
>,
то группа >
 >
разрешима и поэтому >
>
разрешима и поэтому >
 >
- разрешимая группа.
>
- разрешимая группа.
(2) Группа
>
 >
имеет единственную минимальную нормальную
подгруппу
>
имеет единственную минимальную нормальную
подгруппу
> >
и >
>
и >
 >,
>,
где >
 >
- такая максимальная в >
>
- такая максимальная в >
 >
подгруппа, что >
>
подгруппа, что >
 >,
>
>,
>
 >
и >
>
и >
 >.
>.
Так как класс
всех разрешимых групп >
 >
с >
>
с >
 >
образует насыщенную формацию , то ввиду
(1), >
>
образует насыщенную формацию , то ввиду
(1), >
 >
и поэтому в группе >
>
и поэтому в группе >
 >
существует единственная минимальная
нормальная подгруппа >
>
существует единственная минимальная
нормальная подгруппа >
 >.
Из леммы Error: Reference source not found вытекает,
что >
>.
Из леммы Error: Reference source not found вытекает,
что >
 >,
где >
>,
где >
 >
- такая максимальная в >
>
- такая максимальная в >
 >
подгруппа, что >
>
подгруппа, что >
 >
и >
>
и >
 >.
Покажем, что >
>.
Покажем, что >
 >
делит >
>
делит >
 >.
Если >
>.
Если >
 >
не делит >
>
не делит >
 >,
то >
>,
то >
 >
- >
>
- >
 >-группа,
и поэтому >
>-группа,
и поэтому >
 >,
что противоречит выбору группы >
>,
что противоречит выбору группы >
 >.
Итак, >
>.
Итак, >
 >
делит >
>
делит >
 >.
Допустим, что >
>.
Допустим, что >
 >.
Тогда факторгруппа >
>.
Тогда факторгруппа >
 >
изоморфна подгруппе группы автоморфизмов
>
>
изоморфна подгруппе группы автоморфизмов
>
 >.
Так как группа >
>.
Так как группа >
 >
абелева, то >
>
абелева, то >
 >
- сверхразрешимая группа, и поэтому >
>
- сверхразрешимая группа, и поэтому >
 >.
Полученное противоречие с выбором
группы >
>.
Полученное противоречие с выбором
группы >
 >
показывает, что >
>
показывает, что >
 >.
>.
(3) Заключительное противоречие.
Пусть >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
и >
>
и >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Тогда >
>.
Тогда >
 >
и >
>
и >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
такая, что >
>
такая, что >
 >
является максимальной подгруппой группы
>
>
является максимальной подгруппой группы
>
 >.
Покажем, что >
>.
Покажем, что >
 >
- максимальная подгруппы группы >
>
- максимальная подгруппы группы >
 >
и >
>
и >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- собственная подгруппа группы >
>
- собственная подгруппа группы >
 >.
Предположим, что в >
>.
Предположим, что в >
 >
существует подгруппа >
>
существует подгруппа >
 >
такая, что >
>
такая, что >
 >.
Тогда из того, что >
>.
Тогда из того, что >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
следует, что либо >
>,
следует, что либо >
 >,
либо >
>,
либо >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >,
противоречие. Используя приведенные
выше рассуждения видим, что >
>,
противоречие. Используя приведенные
выше рассуждения видим, что >
 >.
Следовательно, >
>.
Следовательно, >
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >.
Рассуждая как выше, мы видим, что >
>.
Рассуждая как выше, мы видим, что >
 >
и >
>
и >
 >
- максимальные подгруппы группы >
>
- максимальные подгруппы группы >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
и >
>
и >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
По условию существует элемент >
>.
По условию существует элемент >
 >
такой, что >
>
такой, что >
 >.
Следовательно,
>.
Следовательно,
> >
>
и поэтому >
 >.
Таким образом, каждая >
>.
Таким образом, каждая >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
перестановочна с каждой максимальной
подгруппой группы >
>
перестановочна с каждой максимальной
подгруппой группы >
 >.
Ввиду (2) и следствия Error: Reference source not found,
получаем, что >
>.
Ввиду (2) и следствия Error: Reference source not found,
получаем, что >
 >,
где силовская >
>,
где силовская >
 >-подгруппа
нормальна в группе >
>-подгруппа
нормальна в группе >
 >.
Значит, >
>.
Значит, >
 >,
где >
>,
где >
 >
и >
>
и >
 >.
Пусть >
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
и >
>-подгруппа
и >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >.
Пусть >
>.
Пусть >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
такая, что >
>
такая, что >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- неединичная подгруппа. Ясно, что >
>
- неединичная подгруппа. Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
и >
>
и >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Следовательно, по условию подгруппа >
>.
Следовательно, по условию подгруппа >
 >
>
>
>
 >-перестановочна
с >
>-перестановочна
с >
 >,
и поэтому для некоторого >
>,
и поэтому для некоторого >
 >
мы имеем >
>
мы имеем >
 >
- подгруппа группы >
>
- подгруппа группы >
 >.
Поскольку >
>.
Поскольку >
 >,
то >
>,
то >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Получили противоречие с тем, что >
>.
Получили противоречие с тем, что >
 >
- минимальная нормальная подгруппа.
Теорема доказана.
>
- минимальная нормальная подгруппа.
Теорема доказана.
Для доказательства теоремы [2.3] нам понадобятся следующие две леммы.
Если все
максимальные подгруппы группы >
 >
имеют простые порядки, то >
>
имеют простые порядки, то >
 >
сверхразрешима.
>
сверхразрешима.
Доказательство.
Так как в группе >
 >
все >
>
все >
 >-максимальные
подгруппы единичны, то ввиду следствия
Error: Reference source not found группа >
>-максимальные
подгруппы единичны, то ввиду следствия
Error: Reference source not found группа >
 >
либо нильпотентна, либо >
>
либо нильпотентна, либо >
 >,
где >
>,
где >
 >
- подгруппа простого порядка >
>
- подгруппа простого порядка >
 >
и >
>
и >
 >
- циклическая >
>
- циклическая >
 >-подгруппа,
которая не является нормальной в >
>-подгруппа,
которая не является нормальной в >
 >
подгруппой (>
>
подгруппой (> >
- различные простые числа). Предположим,
что >
>
- различные простые числа). Предположим,
что >
 >
не является нильпотентной группой.
Тогда >
>
не является нильпотентной группой.
Тогда >
 >.
Поскольку >
>.
Поскольку >
 >,
то >
>,
то >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
и поэтому >
>
и поэтому >
 >.
Так как группа порядка >
>.
Так как группа порядка >
 >
разрешима, то группа >
>
разрешима, то группа >
 >
разрешима. Значит, >
>
разрешима. Значит, >
 >
- нормальная в >
>
- нормальная в >
 >
подгруппа и поэтому главные факторы
группы >
>
подгруппа и поэтому главные факторы
группы >
 >
имеют простые порядки. Следовательно,
>
>
имеют простые порядки. Следовательно,
>
 >
- сверхразрешимая группа. Лемма доказана.
>
- сверхразрешимая группа. Лемма доказана.
Если в
группе >
 >
каждая максимальная подгруппа >
>
каждая максимальная подгруппа >
 >,
индекс >
>,
индекс >
 >
которой является степенью числа >
>
которой является степенью числа >
 >,
нормальна в >
>,
нормальна в >
 >,
то >
>,
то >
 >
- >
>
- >
 >-нильпотентная
группа.
>-нильпотентная
группа.
Доказательство.
Предположим, что данная лемма не верна,
и пусть >
 >
- контрпример минимального порядка.
Тогда:
>
- контрпример минимального порядка.
Тогда:
(1) Для любой
неединичной нормальной подгруппы >
 >
группы >
>
группы >
 >
факторгруппа >
>
факторгруппа >
 >
>
>
>
 >-нильпотентна.
>-нильпотентна.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
такая, что >
>
такая, что >
 >
явяется степенью числа >
>
явяется степенью числа >
 >.
Тогда >
>.
Тогда >
 >
- максимальная в >
>
- максимальная в >
 >
подгруппа и >
>
подгруппа и >
 >
является степенью числа >
>
является степенью числа >
 >.
По условию, >
>.
По условию, >
 >
нормальна в >
>
нормальна в >
 >,
и поэтому >
>,
и поэтому >
 >
нормальна в >
>
нормальна в >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- >
>
- >
 >-нильпотентная
группа.
>-нильпотентная
группа.
(2) Группа
>
 >
имеет единственную минимальную нормальную
подгруппу >
>
имеет единственную минимальную нормальную
подгруппу >
 >
и >
>
и >
 >
- >
>
- >
 >-подгруппа.
>-подгруппа.
Пусть >
 >
- минимальная нормальная подгруппа
группы >
>
- минимальная нормальная подгруппа
группы >
 >.
Так как класс всех >
>.
Так как класс всех >
 >-нильпотентных
групп образует насыщенную формацию, то
ввиду (1), >
>-нильпотентных
групп образует насыщенную формацию, то
ввиду (1), >
 >
и >
>
и >
 >
- единственная минимальная нормальная
подгруппа группы >
>
- единственная минимальная нормальная
подгруппа группы >
 >.
Предположим, что >
>.
Предположим, что >
 >
- >
>
- >
 >-подгруппа.
Тогда >
>-подгруппа.
Тогда >
 >
для некоторой >
>
для некоторой >
 >-холловой
подруппы >
>-холловой
подруппы >
 >
группы >
>
группы >
 >.
Поскольку ввиду (1), >
>.
Поскольку ввиду (1), >
 >
нормальна в >
>
нормальна в >
 >,
то >
>,
то >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >,
противоречие. Следовательно, >
>,
противоречие. Следовательно, >
 >
- элементарная абелева >
>
- элементарная абелева >
 >-подгруппа.
>-подгруппа.
(3) Заключительное противоречие.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
не содержащая >
>,
не содержащая >
 >.
Поскольку >
>.
Поскольку >
 >
абелева, то >
>
абелева, то >
 >
и поэтому >
>
и поэтому >
 >.
Это влечет >
>.
Это влечет >
 >.
Следовательно, >
>.
Следовательно, >
 >
для некоторого >
>
для некоторого >
 >.
Значит, >
>.
Значит, >
 >
- нормальная в >
>
- нормальная в >
 >
подгруппа и поэтому >
>
подгруппа и поэтому >
 >,
противоречие. Лемма доказана.
>,
противоречие. Лемма доказана.
Дополнением к теореме [2.2] является следующий факт.
[2.3]. Пусть
>
 >
- группа, >
>
- группа, >
 >
- ее подгруппа Фиттинга. Если любая
максимальная подгруппа группы >
>
- ее подгруппа Фиттинга. Если любая
максимальная подгруппа группы >
 >
>
>
>
 >-перестановочна
со всеми >
>-перестановочна
со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >,
то группа >
>,
то группа >
 >
разрешима и >
>
разрешима и >
 >
для каждого простого >
>
для каждого простого >
 >.
>.
Доказательство.
Предположим, что теорема не верна, и
пусть >
 >
- контрпример минимального порядка.
>
- контрпример минимального порядка.
(1) >
 >
- непростая группа. Допустим, что >
>
- непростая группа. Допустим, что >
 >.
Поскольку ввиду леммы Error: Reference source not found(3),
условие теоремы выполняется для
факторгруппы >
>.
Поскольку ввиду леммы Error: Reference source not found(3),
условие теоремы выполняется для
факторгруппы >
 >,
то по выбору группы >
>,
то по выбору группы >
 >,
>
>,
>
 >
разрешима и поэтому >
>
разрешима и поэтому >
 >
- разрешимая группа. Полученное
противоречие показывает, что >
>
- разрешимая группа. Полученное
противоречие показывает, что >
 >
и, следовательно, любая максимальная
подгруппа группы >
>
и, следовательно, любая максимальная
подгруппа группы >
 >
перестановочна со всеми >
>
перестановочна со всеми >
 >-максимальными
подгруппами в >
>-максимальными
подгруппами в >
 >.
>.
Предположим,
что все >
 >-максимальные
подгруппы группы >
>-максимальные
подгруппы группы >
 >
единичны. Тогда порядок каждой
>
>
единичны. Тогда порядок каждой
>
 >-максимальной
подгруппа группы >
>-максимальной
подгруппа группы >
 >
является делителем простого числа.
Следовательно, любая максимальная
подгруппа группы >
>
является делителем простого числа.
Следовательно, любая максимальная
подгруппа группы >
 >
либо нильпотентна (порядка >
>
либо нильпотентна (порядка >
 >
или >
>
или >
 >),
либо является ненильпотентной подгруппой
и имеет порядок >
>),
либо является ненильпотентной подгруппой
и имеет порядок >
 >.
Значит, все максимальные подгруппы
сверхразрешимы. Но ввиду теоремы Error: Reference source not found,
мы получаем, что >
>.
Значит, все максимальные подгруппы
сверхразрешимы. Но ввиду теоремы Error: Reference source not found,
мы получаем, что >
 >
разрешима. Это противоречие показывает,
что в группе >
>
разрешима. Это противоречие показывает,
что в группе >
 >
существует неединичная >
>
существует неединичная >
 >-максимальная
подгруппа >
>-максимальная
подгруппа >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
содержащая >
>,
содержащая >
 >.
Тогда для любого >
>.
Тогда для любого >
 >,
>
>,
>
 >.
Если >
>.
Если >
 >,
то ввиду леммы Error: Reference source not found, >
>,
то ввиду леммы Error: Reference source not found, >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >.
Тогда >
>.
Тогда >
 >,
что влечет >
>,
что влечет >
 >.
Следовательно, >
>.
Следовательно, >
 >
- неединичная нормальная подгруппа в >
>
- неединичная нормальная подгруппа в >
 >
и поэтому группа >
>
и поэтому группа >
 >
непроста.
>
непроста.
(2) Для любой
неединичной нормальной в >
 >
подгруппы >
>
подгруппы >
 >
факторгруппа >
>
факторгруппа >
 >
разрешима (это прямо вытекает из леммы
Error: Reference source not found(3)).
>
разрешима (это прямо вытекает из леммы
Error: Reference source not found(3)).
(3) Группа
>
 >
имеет единственную минимальную нормальную
подгруппу >
>
имеет единственную минимальную нормальную
подгруппу >
 >
и >
>
и >
 >,
где >
>,
где >
 >
- такая максимальная в >
>
- такая максимальная в >
 >
подгруппа, что >
>
подгруппа, что >
 >.
>.
Пусть >
 >
- произвольная минимальная нормальная
подгруппа группы >
>
- произвольная минимальная нормальная
подгруппа группы >
 >.
Так как ввиду леммы Error: Reference source not found,
класс всех разрешимых групп c >
>.
Так как ввиду леммы Error: Reference source not found,
класс всех разрешимых групп c >
 >-длиной
>
>-длиной
>
 >
образует насыщенную формацию, то >
>
образует насыщенную формацию, то >
 >
- единственная минимальная нормальная
подгруппа в >
>
- единственная минимальная нормальная
подгруппа в >
 >,
причем >
>,
причем >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
такая, что >
>
такая, что >
 >.
Ясно, что >
>.
Ясно, что >
 >.
Поскольку >
>.
Поскольку >
 >
- единственная минимальная нормальная
подгруппа в >
>
- единственная минимальная нормальная
подгруппа в >
 >,
то >
>,
то >
 >.
>.
(4) >
 >
- разрешимая группа.
>
- разрешимая группа.
Допустим,
что >
 >
- неразрешимая группа. Тогда >
>
- неразрешимая группа. Тогда >
 >
и по выбору группы >
>
и по выбору группы >
 >
мы заключаем, что >
>
мы заключаем, что >
 >
- прямое произведение изоморфных простых
неабелевых групп. Кроме того, и единичная
подгруппа не содержится среди
>
>
- прямое произведение изоморфных простых
неабелевых групп. Кроме того, и единичная
подгруппа не содержится среди
>
 >-максимальных
подгрупп группы >
>-максимальных
подгрупп группы >
 >.
>.
Пусть >
 >
- произвольная >
>
- произвольная >
 >-максимальная
подгруппа, содержащаяся в >
>-максимальная
подгруппа, содержащаяся в >
 >.
Используя приведенные выше рассуждения,
видим, что >
>.
Используя приведенные выше рассуждения,
видим, что >
 >.
Следовательно, порядок любой >
>.
Следовательно, порядок любой >
 >-максимальной
подгруппы группы >
>-максимальной
подгруппы группы >
 >,
содержащейся в >
>,
содержащейся в >
 >,
равен простому числу. Ввиду леммы Error: Reference source not found,
>
>,
равен простому числу. Ввиду леммы Error: Reference source not found,
>
 >
- разрешимая группа. Пусть >
>
- разрешимая группа. Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
содержащая >
>,
содержащая >
 >.
Так >
>.
Так >
 >
- простое число, то либо >
>
- простое число, то либо >
 >,
либо >
>,
либо >
 >.
Пусть имеет место первый случай. Тогда
>
>.
Пусть имеет место первый случай. Тогда
>
 >,
и поскольку >
>,
и поскольку >
 >
- простое число, то >
>
- простое число, то >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Из того, что индекс >
>.
Из того, что индекс >
 >
равен простому числу, следует, что >
>
равен простому числу, следует, что >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
и поэтому >
>
и поэтому >
 >
- >
>
- >
 >-максимальная
подгруппа в >
>-максимальная
подгруппа в >
 >.
Так как >
>.
Так как >
 >
- неабелевая подгруппа, то в ней существует
неединичная максимальная подгруппа >
>
- неабелевая подгруппа, то в ней существует
неединичная максимальная подгруппа >
 >.
Понятно, что >
>.
Понятно, что >
 >
- >
>
- >
 >-максимальная
подгруппа в >
>-максимальная
подгруппа в >
 >
и поэтому по условию перестановочна с
>
>
и поэтому по условию перестановочна с
>
 >.
В таком случае, >
>.
В таком случае, >
 >.
Но >
>.
Но >
 >
- собственная подгруппа в >
>
- собственная подгруппа в >
 >
и поэтому >
>
и поэтому >
 >.
Это противоречие показывает, что >
>.
Это противоречие показывает, что >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Поскольку >
>.
Поскольку >
 >
- простое число, то >
>
- простое число, то >
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >.
Из того, что группа >
>.
Из того, что группа >
 >
есть прямое произведение изоморфных
простых неабелевых групп, следует, что
в >
>
есть прямое произведение изоморфных
простых неабелевых групп, следует, что
в >
 >
имеется неединичная >
>
имеется неединичная >
 >-максимальная
подгруппа >
>-максимальная
подгруппа >
 >.
Тогда >
>.
Тогда >
 >
>
>
>
 >-максимальна
в >
>-максимальна
в >
 >
и следовательно, >
>
и следовательно, >
 >.
Таким образом >
>.
Таким образом >
 >.
Это влечет >
>.
Это влечет >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >
- разрешимая группа.
>
- разрешимая группа.
(5) Заключительное противоречие.
Из (3) и (4)
следует, что >
 >
- элементарная абелева >
>
- элементарная абелева >
 >-группа
для некоторого простого числа >
>-группа
для некоторого простого числа >
 >
и поэтому >
>
и поэтому >
 >.
Покажем, что >
>.
Покажем, что >
 >
делит >
>
делит >
 >.
Если >
>.
Если >
 >
не делит >
>
не делит >
 >,
то >
>,
то >
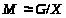 >
- >
>
- >
 >-группа,
и поэтому >
>-группа,
и поэтому >
 >,
что противоречит выбору группы >
>,
что противоречит выбору группы >
 >.
Итак, >
>.
Итак, >
 >
делит >
>
делит >
 >.
Ввиду леммы Error: Reference source not found, >
>.
Ввиду леммы Error: Reference source not found, >
 >.
>.
Пусть >
 >
- произвольная максимальная в >
>
- произвольная максимальная в >
 >
подгруппа с индексом >
>
подгруппа с индексом >
 >,
где >
>,
где >
 >
и >
>
и >
 >.
Тогда >
>.
Тогда >
 >,
где >
>,
где >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >.
>.
Предположим,
что >
 >
не является нормальной в >
>
не является нормальной в >
 >
подгруппой. Ясно, что >
>
подгруппой. Ясно, что >
 >
- максимальная в >
>
- максимальная в >
 >
подгруппа. Если >
>
подгруппа. Если >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >,
то >
>,
то >
 >.
Значит, >
>.
Значит, >
 >
не является нормальной подгруппой в >
>
не является нормальной подгруппой в >
 >.
Пусть >
>.
Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >.
Тогда >
>.
Тогда >
 >
- >
>
- >
 >-максимальная
в >
>-максимальная
в >
 >
подгруппа и поэтому >
>
подгруппа и поэтому >
 >
- >
>
- >
 >-максимальная
в >
>-максимальная
в >
 >
подгруппа для любого >
>
подгруппа для любого >
 >.
Поскольку по условию >
>.
Поскольку по условию >
 >
>
>
>
 >-перестановочна
с подгруппой >
>-перестановочна
с подгруппой >
 >
и >
>
и >
 >,
то >
>,
то >
 >
перестановочна с подгруппой >
>
перестановочна с подгруппой >
 >
и поэтому >
>
и поэтому >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
в >
>-максимальная
в >
 >
подгруппа. Так как >
>
подгруппа. Так как >
 >
и >
>
и >
 >
не является нормальной подгруппой в >
>
не является нормальной подгруппой в >
 >,
то >
>,
то >
 >
и поэтому >
>
и поэтому >
 >
- нормальная погруппа в >
>
- нормальная погруппа в >
 >.
Следовательно, >
>.
Следовательно, >
 >
- нормальная в >
>
- нормальная в >
 >
подгруппа. Это влечет, что >
>
подгруппа. Это влечет, что >
 >.
Ввиду произвольного выбора >
>.
Ввиду произвольного выбора >
 >,
получаем, что каждая максимальная
подгруппа группы >
>,
получаем, что каждая максимальная
подгруппа группы >
 >
нормальна в >
>
нормальна в >
 >.
Значит, >
>.
Значит, >
 >
- нильпотентная группа и любая максимальная
подгруппа в >
>
- нильпотентная группа и любая максимальная
подгруппа в >
 >
нормальна в >
>
нормальна в >
 >.
Предположим, что >
>.
Предположим, что >
 >.
Поскольку >
>.
Поскольку >
 >
и >
>
и >
 >
разрешима, то в группе >
>
разрешима, то в группе >
 >
существует минимальная нормальная
>
>
существует минимальная нормальная
>
 >-подгруппа
>
>-подгруппа
>
 >,
где >
>,
где >
 >.
Так как >
>.
Так как >
 >
- максимальная в >
>
- максимальная в >
 >
подгруппа, то >
>
подгруппа, то >
 >.
Это влечет, что >
>.
Это влечет, что >
 >.
Следовательно, группа >
>.
Следовательно, группа >
 >
обладает главным рядом
>
обладает главным рядом
> >
>
и поэтому >
 >.
Полученное противоречие с выбором
группы >
>.
Полученное противоречие с выбором
группы >
 >
показывает, что >
>
показывает, что >
 >.
Пусть >
>.
Пусть >
 >
- такая максимальная подгруппа группы
>
>
- такая максимальная подгруппа группы
>
 >,
что >
>,
что >
 >.
Тогда >
>.
Тогда >
 >.
Это влечет >
>.
Это влечет >
 >,
что противоречие тому, что >
>,
что противоречие тому, что >
 >.
>.
Следовательно,
>
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Согласно лемме Error: Reference source not found, >
>.
Согласно лемме Error: Reference source not found, >
 >
- >
>
- >
 >-нильпотентная
группа и поэтому >
>-нильпотентная
группа и поэтому >
 >.
Ввиду произвольного выбора >
>.
Ввиду произвольного выбора >
 >,
получаем, что >
>,
получаем, что >
 >
для любого >
>
для любого >
 >
и >
>
и >
 >.
Ясно, что >
>.
Ясно, что >
 >,
что противоречит >
>,
что противоречит >
 >.
Теорема доказана.
>.
Теорема доказана.
3.
Группы, в которых >
 >-максимальные
подгруппы перестановочны с >
>-максимальные
подгруппы перестановочны с >
 >-максимальными
подгруппами
>-максимальными
подгруппами
Целью данного
раздела является описание ненильпотентных
групп, у которых каждая >
 >-максимальная
подгруппа перестановочна со всеми
>
>-максимальная
подгруппа перестановочна со всеми
>
 >-максимальными
подгруппами.
>-максимальными
подгруппами.
Для доказательства основного результата данного раздела нам понадобится следующая лемма.
[3.1]. Пусть
>
 >
- группа Шмидта. Тогда в том и только том
случае каждая 2-максимальная подгруппа
группы >
>
- группа Шмидта. Тогда в том и только том
случае каждая 2-максимальная подгруппа
группы >
 >
перестановочна со всеми 3-максимальными
подгруппами группы >
>
перестановочна со всеми 3-максимальными
подгруппами группы >
 >,
когда группа >
>,
когда группа >
 >
имеет вид:
>
имеет вид:
(1) >
 >
- группа Миллера-Морено;
>
- группа Миллера-Морено;
(2) >
 >,
где >
>,
где >
 >
- группа кватернионов порядка >
>
- группа кватернионов порядка >
 >,
>
>,
>
 >
- группа порядка >
>
- группа порядка >
 >.
>.
Доказательство.
Необходимость. Предположим, что >
 >
- группа Шмидта, у которой каждая
2-максимальная подгруппа группы >
>
- группа Шмидта, у которой каждая
2-максимальная подгруппа группы >
 >
перестановочна со всеми 3-максимальными
подгруппами группы >
>
перестановочна со всеми 3-максимальными
подгруппами группы >
 >.
Докажем, что в этом случае, либо >
>.
Докажем, что в этом случае, либо >
 >
- группа Миллера-Морено, либо >
>
- группа Миллера-Морено, либо >
 >,
где >
>,
где >
 >
- группа кватернионов порядка >
>
- группа кватернионов порядка >
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >.
Предположим, что это не так и пусть >
>.
Предположим, что это не так и пусть >
 >
- контрпример минимального порядка.
>
- контрпример минимального порядка.
Так как >
 >
- группа Шмидта, то ввиду леммы Error: Reference source not found(I),
>
>
- группа Шмидта, то ввиду леммы Error: Reference source not found(I),
>
 >,
где >
>,
где >
 >
- силовская >
>
- силовская >
 >-подгруппа
в >
>-подгруппа
в >
 >,
>
>,
>
 >
- циклическая >
>
- циклическая >
 >-подгруппа.
>-подгруппа.
Покажем, что
>
 >
- группа простого порядка. Предположим,
что это не так. Тогда в группе >
>
- группа простого порядка. Предположим,
что это не так. Тогда в группе >
 >
имеется собственная подгруппа >
>
имеется собственная подгруппа >
 >
простого порядка. Ввиду леммы Error: Reference source not found(IV),
>
>
простого порядка. Ввиду леммы Error: Reference source not found(IV),
>
 >
и, следовательно, >
>
и, следовательно, >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >
и >
>
и >
 >
- группа Шмидта.
>
- группа Шмидта.
Понятно, что
в группе >
 >
каждая 2-максимальная подгруппа группы
>
>
каждая 2-максимальная подгруппа группы
>
 >
перестановочна со всеми 3-максимальными
подгруппами группы >
>
перестановочна со всеми 3-максимальными
подгруппами группы >
 >.
>.
Поскольку
>
 >,
то >
>,
то >
 >
и поэтому по выбору группы >
>
и поэтому по выбору группы >
 >
мы заключаем, что либо >
>
мы заключаем, что либо >
 >
- группа Миллера-Морено, либо >
>
- группа Миллера-Морено, либо >
 >,
где >
>,
где >
 >
- группа кватернионов порядка >
>
- группа кватернионов порядка >
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >.
>.
В первом
случае >
 >
- абелева подгруппа и, следовательно, >
>
- абелева подгруппа и, следовательно, >
 >
- группа Миллера-Морено. Полученное
противоречие с выбором группы >
>
- группа Миллера-Морено. Полученное
противоречие с выбором группы >
 >
показывает, что >
>
показывает, что >
 >,
где >
>,
где >
 >
- группа кватернионов порядка >
>
- группа кватернионов порядка >
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >.
Тогда >
>.
Тогда >
 >,
где >
>,
где >
 >
- группа кватернионов порядка >
>
- группа кватернионов порядка >
 >
и >
>
и >
 >
- циклическая группа порядка >
>
- циклическая группа порядка >
 >.
Пусть >
>.
Пусть >
 >
- такая максимальная подгруппа группы
>
>
- такая максимальная подгруппа группы
>
 >,
что >
>,
что >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >.
Поскольку >
>.
Поскольку >
 >
- группа Шмидта, то >
>
- группа Шмидта, то >
 >
нильпотентна, и поэтому >
>
нильпотентна, и поэтому >
 >.
Это означает, что >
>.
Это означает, что >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >.
Следовательно, >
>.
Следовательно, >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Понятно, что >
>.
Понятно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Пусть >
>.
Пусть >
 >
- подгруппа группы >
>
- подгруппа группы >
 >
с индексом >
>
с индексом >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-макимальная
подгруппа группы >
>-макимальная
подгруппа группы >
 >.
Так как по условию >
>.
Так как по условию >
 >
и >
>
и >
 >
перестановочны, то >
>
перестановочны, то >
 >
- подгруппа группы >
>
- подгруппа группы >
 >,
индекс которой равен >
>,
индекс которой равен >
 >.
Рассуждая как выше, видим, что >
>.
Рассуждая как выше, видим, что >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >
- группа простого порядка.
>
- группа простого порядка.
Пусть >
 >
- произвольная максимальная подгрупа
в >
>
- произвольная максимальная подгрупа
в >
 >
и >
>
и >
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >.
Так как >
>.
Так как >
 >
неабелева, то >
>
неабелева, то >
 >
- неединичная подгруппа. Из того, что >
>
- неединичная подгруппа. Из того, что >
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >,
следует, что >
>,
следует, что >
 >
- 3-максимальная подгруппа в >
>
- 3-максимальная подгруппа в >
 >.
>.
Ввиду леммы
(II), >
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >.
Рассмотрим максимальную в >
>.
Рассмотрим максимальную в >
 >
подгруппу >
>
подгруппу >
 >,
такую что >
>,
такую что >
 >.
Тогда
>.
Тогда
> >
>
и >
 >
- 2-максимальная подгруппа в >
>
- 2-максимальная подгруппа в >
 >.
По условию подгруппы >
>.
По условию подгруппы >
 >
и >
>
и >
 >
перестановочны. Если >
>
перестановочны. Если >
 >,
то используя лемму (V), имеем
>,
то используя лемму (V), имеем
> >
>
Из того, что
>
 >
получаем, что порядок >
>
получаем, что порядок >
 >
делит >
>
делит >
 >.
Поскольку >
>.
Поскольку >
 >,
то полученное противоречие показывает,
что >
>,
то полученное противоречие показывает,
что >
 >
- собственная подгруппа группы >
>
- собственная подгруппа группы >
 >.
Следовательно, >
>.
Следовательно, >
 >
нильпотентна, и поэтому
>
нильпотентна, и поэтому
> >
>
Значит, либо
>
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >,
либо >
>,
либо >
 >.
В первом случае получаем, что >
>.
В первом случае получаем, что >
 >
является единственной максимальной
подгруппой в >
>
является единственной максимальной
подгруппой в >
 >.
Это означает, что >
>.
Это означает, что >
 >
- циклическая подгруппа, что противоречит
выбору группы >
>
- циклическая подгруппа, что противоречит
выбору группы >
 >.
Следовательно, первый случай невозможен.
Итак, >
>.
Следовательно, первый случай невозможен.
Итак, >
 >.
Ввиду произвольного выбора >
>.
Ввиду произвольного выбора >
 >
получаем, что >
>
получаем, что >
 >
- единственная >
>
- единственная >
 >-максимальная
подгруппа в группе >
>-максимальная
подгруппа в группе >
 >.
Из теоремы Error: Reference source not found следует,
что >
>.
Из теоремы Error: Reference source not found следует,
что >
 >
- либо циклическая группа, либо группа
кватернионов порядка >
>
- либо циклическая группа, либо группа
кватернионов порядка >
 >.
Так как первый случай очевидно невозможен,
то >
>.
Так как первый случай очевидно невозможен,
то >
 >
- группа кватернионов порядка >
>
- группа кватернионов порядка >
 >.
Поскольку подгруппа >
>.
Поскольку подгруппа >
 >
изоморфна погруппе группы автоморфизмов
>
>
изоморфна погруппе группы автоморфизмов
>
 >,
то >
>,
то >
 >.
Полученное противоречие с выбором
группы >
>.
Полученное противоречие с выбором
группы >
 >
доказывает, что либо >
>
доказывает, что либо >
 >
- группа Миллера-Морена, либо >
>
- группа Миллера-Морена, либо >
 >,
где >
>,
где >
 >
- группа кватернионов порядка >
>
- группа кватернионов порядка >
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >.
>.
Достаточность очевидна. Лемма доказана.
Error: Reference source not found.
В ненильпотентной группе >
 >
каждая >
>
каждая >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
перестановочна со всеми >
>
перестановочна со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >
тогда и только тогда, когда группа >
>
тогда и только тогда, когда группа >
 >
имеет вид:
>
имеет вид:
(1) >
 >
- группа Миллера-Морена;
>
- группа Миллера-Морена;
(2) >
 >
- группа Шмидта, где >
>
- группа Шмидта, где >
 >
- группа кватернионов порядка >
>
- группа кватернионов порядка >
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >;
>;
(3) >
 >
и >
>
и >
 >,
>,
где >
 >
- группа простого порядка >
>
- группа простого порядка >
 >,
>
>,
>
 >
- нециклическая >
>
- нециклическая >
 >-группа
и все ее максимальные подгруппы, отличные
от >
>-группа
и все ее максимальные подгруппы, отличные
от >
 >,
цикличны;
>,
цикличны;
(4) >
 >,
>,
где >
 >
- группа порядка >
>
- группа порядка >
 >,
>
>,
>
 >
- группа простого порядка >
>
- группа простого порядка >
 >,
отличного от >
>,
отличного от >
 >;
>;
(5) >
 >,
>,
где >
 >
- группа порядка >
>
- группа порядка >
 >,
каждая подгруппа которой нормальна в
группе >
>,
каждая подгруппа которой нормальна в
группе >
 >,
>
>,
>
 >
- циклическая >
>
- циклическая >
 >-группа
и >
>-группа
и >
 >;
>;
(6) >
 >,
>,
где >
 >
- примарная циклическая группа порядка
>
>
- примарная циклическая группа порядка
>
 >,
>
>,
>
 >
- группа простого порядка >
>
- группа простого порядка >
 >,
где >
>,
где >
 >
и >
>
и >
 >;
>;
(7) >
 >,
>,
где >
 >
и >
>
и >
 >
- группы простых порядков >
>
- группы простых порядков >
 >
и >
>
и >
 >
(>
>
(> >),
>
>),
>
 >
- циклическая >
>
- циклическая >
 >-подгруппа
в >
>-подгруппа
в >
 >
(>
>
(> >),
которая не является нормальной в >
>),
которая не является нормальной в >
 >,
но максимальная подгруппа которой
нормальна в >
>,
но максимальная подгруппа которой
нормальна в >
 >.
>.
Доказательство.
Необходимость. Пусть >
 >
- ненильпотентная группа, у которой
каждая 2-максимальная подгруппа группы
>
>
- ненильпотентная группа, у которой
каждая 2-максимальная подгруппа группы
>
 >
перестановочна со всеми 3-максимальными
подгруппами группы >
>
перестановочна со всеми 3-максимальными
подгруппами группы >
 >.
>.
Если в группе
>
 >
все максимальные подгруппы нильпотентны,
то группа >
>
все максимальные подгруппы нильпотентны,
то группа >
 >
является группой Шмидта. Ввиду леммы,
группа >
>
является группой Шмидта. Ввиду леммы,
группа >
 >
оказывается группой типа (1) или типа
(2).
>
оказывается группой типа (1) или типа
(2).
Итак, мы можем
предположить, что в группе >
 >
существует ненильпотентная максимальная
подгруппа.
>
существует ненильпотентная максимальная
подгруппа.
Из теоремы
следует, что группа >
 >
разрешима. Так как в разрешимой группе
индекс любой максимальной подгруппы
является степенью простого числа, то
>
>
разрешима. Так как в разрешимой группе
индекс любой максимальной подгруппы
является степенью простого числа, то
>
 >.
>.
I. >
 >.
>.
Пусть >
 >
- некоторая силовская >
>
- некоторая силовская >
 >-подгруппа
в >
>-подгруппа
в >
 >
и >
>
и >
 >
- некоторая силовская >
>
- некоторая силовская >
 >-подгруппа
в >
>-подгруппа
в >
 >,
где >
>,
где >
 >.
>.
Предположим,
что в группе >
 >
нет нормальных силовских подгрупп. Так
как группа >
>
нет нормальных силовских подгрупп. Так
как группа >
 >
разрешима, то в >
>
разрешима, то в >
 >
существует нормальная подгруппа >
>
существует нормальная подгруппа >
 >
простого индекса, скажем индекса >
>
простого индекса, скажем индекса >
 >,
и она не является нильпотентной группой.
Действительно, если >
>,
и она не является нильпотентной группой.
Действительно, если >
 >
нильпотентна, то в ней нормальна силовская
>
>
нильпотентна, то в ней нормальна силовская
>
 >-подгруппа
>
>-подгруппа
>
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Из того, что >
>.
Из того, что >
 >
следует, что >
>
следует, что >
 >
- нормальная силовская >
>
- нормальная силовская >
 >-подгруппа
в >
>-подгруппа
в >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >
не является нильпотентной подгруппой.
>
не является нильпотентной подгруппой.
Так как >
 >
является максимальной подгруппой в >
>
является максимальной подгруппой в >
 >,
то по условию все 2-максимальные подгруппы
группы >
>,
то по условию все 2-максимальные подгруппы
группы >
 >
перестановочны с каждой максимальной
подгруппой группы >
>
перестановочны с каждой максимальной
подгруппой группы >
 >.
Ввиду следствия Error: Reference source not found,
группа >
>.
Ввиду следствия Error: Reference source not found,
группа >
 >
имеет вид >
>
имеет вид >
 >,
где >
>,
где >
 >
- группа простого порядка >
>
- группа простого порядка >
 >
и >
>
и >
 >
- циклическая >
>
- циклическая >
 >-подгруппа.
>-подгруппа.
Так как
> >
>
и факторгруппа
>
 >
изоморфна подгруппе из >
>
изоморфна подгруппе из >
 >,
то >
>,
то >
 >
больше >
>
больше >
 >.
>.
Если >
 >
- нильпотентная группа, то >
>
- нильпотентная группа, то >
 >
и поэтому согласно теореме Бернсайда
Error: Reference source not found, группа >
>
и поэтому согласно теореме Бернсайда
Error: Reference source not found, группа >
 >
>
>
>
 >-нильпотентна.
Но тогда >
>-нильпотентна.
Но тогда >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >
является ненильпотентной группой. Так
как >
>
является ненильпотентной группой. Так
как >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >,
то ввиду следствия Error: Reference source not found,
подгруппа >
>,
то ввиду следствия Error: Reference source not found,
подгруппа >
 >
имеет вид >
>
имеет вид >
 >,
где >
>,
где >
 >
- циклическая >
>
- циклическая >
 >-подгруппа,
и, следовательно, >
>-подгруппа,
и, следовательно, >
 >.
Полученное противоречие показывает,
что в группе >
>.
Полученное противоречие показывает,
что в группе >
 >
существует нормальная силовская
подгруппа.
>
существует нормальная силовская
подгруппа.
Пусть,
например, такой является силовская
>
 >-подгруппа
>
>-подгруппа
>
 >
группы >
>
группы >
 >.
Пусть >
>.
Пусть >
 >.
Ясно, что >
>.
Ясно, что >
 >.
>.
Если в группе
>
 >
существует подгруппа Шмидта >
>
существует подгруппа Шмидта >
 >,
индекс которой равен >
>,
индекс которой равен >
 >,
то >
>,
то >
 >.
Ввиду следствия Error: Reference source not found, >
>.
Ввиду следствия Error: Reference source not found, >
 >
- группа порядка >
>
- группа порядка >
 >.
>.
Пусь >
 >.
Допустим, что >
>.
Допустим, что >
 >
- циклическая подгруппа. В этом случае,
группа >
>
- циклическая подгруппа. В этом случае,
группа >
 >
является группой Шмидта. Полученное
противоречие с выбором группы >
>
является группой Шмидта. Полученное
противоречие с выбором группы >
 >
показывает, что >
>
показывает, что >
 >
- нециклическая подгруппа. Пусть >
>
- нециклическая подгруппа. Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >,
отличная от >
>,
отличная от >
 >.
Если >
>.
Если >
 >
- нильпотентная подгруппа, то группа >
>
- нильпотентная подгруппа, то группа >
 >
нильпотентна, противоречие. Следовательно,
>
>
нильпотентна, противоречие. Следовательно,
>
 >
- группа Шмидта, и поэтому >
>
- группа Шмидта, и поэтому >
 >
- циклическая подгруппа. Таким образом,
группа >
>
- циклическая подгруппа. Таким образом,
группа >
 >
относится к типу (3).
>
относится к типу (3).
Пусть >
 >.
Тогда >
>.
Тогда >
 >.
Следовательно, >
>.
Следовательно, >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Пусть >
>.
Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >.
Если >
>.
Если >
 >
- нильпотентная подгруппа, то >
>
- нильпотентная подгруппа, то >
 >,
и поэтому >
>,
и поэтому >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >
- группа Шмидта. Значит, >
>
- группа Шмидта. Значит, >
 >
- циклическая подгруппа. Пусть >
>
- циклическая подгруппа. Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >,
отличная от >
>,
отличная от >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- единственная >
>
- единственная >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Факторгруппа >
>.
Факторгруппа >
 >,
где >
>,
где >
 >
- элементарная абелева подгруппа порядка
>
>
- элементарная абелева подгруппа порядка
>
 >
и >
>
и >
 >.
Так как >
>.
Так как >
 >
- неприводимая абелева группа автоморфизмов
группы >
>
- неприводимая абелева группа автоморфизмов
группы >
 >,
то >
>,
то >
 >
- циклическая группа, и поэтому подгруппа
>
>
- циклическая группа, и поэтому подгруппа
>
 >
циклическая, противоречие.
>
циклическая, противоречие.
Предположим
теперь, что у всех подгрупп Шмидта индекс
в группе >
 >
является степенью числа >
>
является степенью числа >
 >.
>.
Так как в
группе >
 >
существуют собственные подгруппы
Шмидта, то >
>
существуют собственные подгруппы
Шмидта, то >
 >.
Пусть >
>.
Пусть >
 >
- подгруппа Шмидта группы >
>
- подгруппа Шмидта группы >
 >.
Тогда >
>.
Тогда >
 >
для некоторого >
>
для некоторого >
 >.
Понятно, что для некоторого >
>.
Понятно, что для некоторого >
 >
имеет место >
>
имеет место >
 >
и поэтому не теряя общности мы может
полагать, что >
>
и поэтому не теряя общности мы может
полагать, что >
 >.
Поскольку >
>.
Поскольку >
 >,
то >
>,
то >
 >.
Из того, что >
>.
Из того, что >
 >,
следует, что >
>,
следует, что >
 >.
>.
Так как >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
то по условию 2-максимальные подгруппы
группы >
>,
то по условию 2-максимальные подгруппы
группы >
 >
перестановочны со всеми максимальными
подгруппами в >
>
перестановочны со всеми максимальными
подгруппами в >
 >.
Используя следствие, мы видим, что >
>.
Используя следствие, мы видим, что >
 >
- группа простого порядка и >
>
- группа простого порядка и >
 >
- циклическая подгруппа, причем все
собственные подгруппы группы >
>
- циклическая подгруппа, причем все
собственные подгруппы группы >
 >
нормальны в >
>
нормальны в >
 >.
Следовательно, >
>.
Следовательно, >
 >
является максимальной подгруппой группы
>
>
является максимальной подгруппой группы
>
 >.
>.
Предположим,
что >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Тогда >
>.
Тогда >
 >.
Из того, что >
>.
Из того, что >
 >,
следует, что >
>,
следует, что >
 >
- нильпотентная максимальная подгруппа
в >
>
- нильпотентная максимальная подгруппа
в >
 >.
Значит, >
>.
Значит, >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Поскольку >
>.
Поскольку >
 >
нормальна в >
>
нормальна в >
 >,
то >
>,
то >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >.
Так как >
>.
Так как >
 >,
то в группе >
>,
то в группе >
 >
существует 2-максимальная подгруппа >
>
существует 2-максимальная подгруппа >
 >
такая, что >
>
такая, что >
 >.
Тогда >
>.
Тогда >
 >
- >
>
- >
 >-максимальная
подгруппа в >
>-максимальная
подгруппа в >
 >,
и следовательно, >
>,
и следовательно, >
 >
- >
>
- >
 >-максимальная
подгруппа в >
>-максимальная
подгруппа в >
 >.
Поскольку по условию >
>.
Поскольку по условию >
 >
перестановочна с >
>
перестановочна с >
 >,
то
>,
то
> >
>
что приводит
к противоречию с максимальностью
подгруппы >
 >.
Следовательно, >
>.
Следовательно, >
 >.
>.
Предположим
теперь, что >
 >.
Допустим, что >
>.
Допустим, что >
 >.
Пусть >
>.
Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >
и >
>
и >
 >
- произвольная >
>
- произвольная >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Рассуждая как выше видим, что >
>.
Рассуждая как выше видим, что >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >
и поэтому >
>
и поэтому >
 >
- подгруппа группы >
>
- подгруппа группы >
 >.
Используя приведенные выше рассуждения
видим, что >
>.
Используя приведенные выше рассуждения
видим, что >
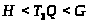 >.
Полученное противоречие с максимальностью
подгруппы >
>.
Полученное противоречие с максимальностью
подгруппы >
 >
показывает, что >
>
показывает, что >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
такая что >
>,
такая что >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- абелева и поэтому >
>
- абелева и поэтому >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >.
Из того, что
>.
Из того, что
> >
>
получаем,
что >
 >,
и поэтому >
>,
и поэтому >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
>.
Предположим,
что в группе >
 >
существует подгруппа >
>
существует подгруппа >
 >
порядка >
>
порядка >
 >,
отличная от >
>,
отличная от >
 >.
Из того, что порядок >
>.
Из того, что порядок >
 >
следует, что >
>
следует, что >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Так как по условию подгруппы >
>.
Так как по условию подгруппы >
 >
и >
>
и >
 >
перестановочны, то мы имеем
>
перестановочны, то мы имеем
> >
>
Следовательно,
>
 >
- подгруппа группы >
>
- подгруппа группы >
 >,
и поэтому
>,
и поэтому
> >
>
Это противоречие
показывает, что в группе >
 >
существует единственная подгруппа
порядка >
>
существует единственная подгруппа
порядка >
 >.
Ввиду теоремы Error: Reference source not found, группа
>
>.
Ввиду теоремы Error: Reference source not found, группа
>
 >
является либо группой кватернионов
порядка >
>
является либо группой кватернионов
порядка >
 >,
либо является циклической группой
порядка >
>,
либо является циклической группой
порядка >
 >.
В первом случае, подгруппа >
>.
В первом случае, подгруппа >
 >
порядка >
>
порядка >
 >
группы >
>
группы >
 >
содержится в центре >
>
содержится в центре >
 >
группы >
>
группы >
 >,
и поэтому подгруппа >
>,
и поэтому подгруппа >
 >
не является группой Шмидта, противоречие.
Следовательно, мы имеем второй случай.
Значит, >
>
не является группой Шмидта, противоречие.
Следовательно, мы имеем второй случай.
Значит, >
 >
- циклическая подгруппа порядка >
>
- циклическая подгруппа порядка >
 >.
Понятно, что >
>.
Понятно, что >
 >.
Если >
>.
Если >
 >,
то подгруппа >
>,
то подгруппа >
 >
нормальна в группе >
>
нормальна в группе >
 >,
и поэтому >
>,
и поэтому >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >.
Таким образом, >
>.
Таким образом, >
 >
- группа типа (6). Пусть теперь >
>
- группа типа (6). Пусть теперь >
 >.
Если порядок >
>.
Если порядок >
 >,
то >
>,
то >
 >,
и поэтому >
>,
и поэтому >
 >
- группа типа (4). Предположим, что порядок
>
>
- группа типа (4). Предположим, что порядок
>
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
и >
>
и >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Из того, что >
>.
Из того, что >
 >,
следует, что >
>,
следует, что >
 >
- неединичная подгруппа. Так как подгруппа
>
>
- неединичная подгруппа. Так как подгруппа
>
 >
нильпотентна, то >
>
нильпотентна, то >
 >.
Но как мы уже знаем, >
>.
Но как мы уже знаем, >
 >
- циклическая подгруппа и поэтому >
>
- циклическая подгруппа и поэтому >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Пусть >
>.
Пусть >
 >
- произвольная подгруппа порядка >
>
- произвольная подгруппа порядка >
 >
группы >
>
группы >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
и >
>
и >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Значит, по условию подгруппы >
>.
Значит, по условию подгруппы >
 >
и >
>
и >
 >
перестановочны. Так как >
>
перестановочны. Так как >
 >
- абелева подгруппа, то >
>
- абелева подгруппа, то >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Заметим, что поскольку >
>.
Заметим, что поскольку >
 >,
то
>,
то
> >
>
является
нормальной подгруппой в >
 >
и поэтому >
>
и поэтому >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Это означает, что >
>.
Это означает, что >
 >
- группа типа (5).
>
- группа типа (5).
II. >
 >.
>.
Пусть >
 >
- некоторая силовская >
>
- некоторая силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >,
>
>,
>
 >
- некоторая силовская >
>
- некоторая силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >
и >
>
и >
 >
- некоторая силовская >
>
- некоторая силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >,
где >
>,
где >
 >
- различные простые делители порядка
группы >
>
- различные простые делители порядка
группы >
 >.
Пусть >
>.
Пусть >
 >
- произвольная нормальная максимальная
подгруппа группы >
>
- произвольная нормальная максимальная
подгруппа группы >
 >.
Так как >
>.
Так как >
 >
- разрешимая группа, то индекс подгруппы
>
>
- разрешимая группа, то индекс подгруппы
>
 >
в группе >
>
в группе >
 >
равен некоторому простому числу. Пусть,
например, индекс >
>
равен некоторому простому числу. Пусть,
например, индекс >
 >
равен >
>
равен >
 >.
Ввиду следствия Error: Reference source not found, >
>.
Ввиду следствия Error: Reference source not found, >
 >
- либо нильпотентная подгруппа, либо
ненильпотентная группа порядка >
>
- либо нильпотентная подгруппа, либо
ненильпотентная группа порядка >
 >.
>.
1. Предположим,
что >
 >
- нильпотентная подгруппа. Пусть >
>
- нильпотентная подгруппа. Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >,
>
>,
>
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >
и >
>
и >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >.
Тогда >
>.
Тогда >
 >.
Так как >
>.
Так как >
 >
и >
>
и >
 >,
то >
>,
то >
 >
и >
>
и >
 >
- нормальные подгруппы в группе >
>
- нормальные подгруппы в группе >
 >.
Из того, что индекс подгруппы >
>.
Из того, что индекс подгруппы >
 >
равен >
>
равен >
 >,
следует, что >
>,
следует, что >
 >
и >
>
и >
 >
- силовские подгруппы группы >
>
- силовские подгруппы группы >
 >
и поэтому >
>
и поэтому >
 >
и >
>
и >
 >.
Понятно, что для некоторого >
>.
Понятно, что для некоторого >
 >
имеет место >
>
имеет место >
 >
и поэтому, не теряя общности, мы можем
полагать, что >
>
и поэтому, не теряя общности, мы можем
полагать, что >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Ясно, что >
>.
Ясно, что >
 >
не является нормальной подгруппой в
группе >
>
не является нормальной подгруппой в
группе >
 >.
>.
Если подгруппы
>
 >
и >
>
и >
 >
нильпотентны, то >
>
нильпотентны, то >
 >
и >
>
и >
 >,
и поэтому >
>,
и поэтому >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Значит, подгруппы >
>.
Значит, подгруппы >
 >
и >
>
и >
 >
не могут быть обе нильпотентными
подгруппами. Следовательно, возможны
следующие случаи.
>
не могут быть обе нильпотентными
подгруппами. Следовательно, возможны
следующие случаи.
а) >
 >
и >
>
и >
 >
- группы Шмидта.
>
- группы Шмидта.
Так как >
 >,
то ввиду следствия Error: Reference source not found,
>
>,
то ввиду следствия Error: Reference source not found,
>
 >
- подгруппа простого порядка >
>
- подгруппа простого порядка >
 >
и >
>
и >
 >
- циклическая подгруппа, которая не
является нормальной в группе >
>
- циклическая подгруппа, которая не
является нормальной в группе >
 >,
но максимальная подгруппа >
>,
но максимальная подгруппа >
 >
группы >
>
группы >
 >
нормальна в >
>
нормальна в >
 >.
Аналогично видим, что >
>.
Аналогично видим, что >
 >
- подгруппа простого порядка >
>
- подгруппа простого порядка >
 >
и >
>
и >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >,
и поэтому >
>,
и поэтому >
 >
является группой типа (7).
>
является группой типа (7).
б) Одна из
подгрупп >
 >,
>
>,
>
 >
является нильпотентной, а другая -
группой Шмидта.
>
является нильпотентной, а другая -
группой Шмидта.
Пусть например,
>
 >
- группа Шмидта и >
>
- группа Шмидта и >
 >
- нильпотентная подгруппа. Из следствия
следует, что >
>
- нильпотентная подгруппа. Из следствия
следует, что >
 >
- группа простого порядка >
>
- группа простого порядка >
 >,
>
>,
>
 >
- циклическая группа и максимальная
подгруппа >
>
- циклическая группа и максимальная
подгруппа >
 >
из >
>
из >
 >
нормальна в >
>
нормальна в >
 >.
Так как >
>.
Так как >
 >
- нильпотентная группа, то >
>
- нильпотентная группа, то >
 >.
Из того, что >
>.
Из того, что >
 >
следует, что >
>
следует, что >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Значит, ввиду леммы Error: Reference source not found,
>
>.
Значит, ввиду леммы Error: Reference source not found,
>
 >
- нормальная максимальная подгруппа в
группе >
>
- нормальная максимальная подгруппа в
группе >
 >
и поэтому >
>
и поэтому >
 >.
Следовательно, >
>.
Следовательно, >
 >
- группа простого порядка >
>
- группа простого порядка >
 >.
>.
Из того, что
>
 >
- нильпотентная подгруппа и >
>
- нильпотентная подгруппа и >
 >
- циклическая группа следует, что >
>
- циклическая группа следует, что >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Следовательно, >
>.
Следовательно, >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >,
т.е. >
>,
т.е. >
 >
- группа типа (7).
>
- группа типа (7).
2. Предположим
теперь, что >
 >
- ненильпотентная группа.
>
- ненильпотентная группа.
Из следствия
следует, что >
 >,
где >
>,
где >
 >
- группа простого порядка >
>
- группа простого порядка >
 >
и >
>
и >
 >
- циклическая группа, которая не является
нормальной в группе >
>
- циклическая группа, которая не является
нормальной в группе >
 >,
но максимальная подгруппа >
>,
но максимальная подгруппа >
 >
из >
>
из >
 >
нормальна в >
>
нормальна в >
 >.
Так как >
>.
Так как >
 >
- характеристическая подгруппа в >
>
- характеристическая подгруппа в >
 >
и >
>
и >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >,
то >
>,
то >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Из того, что >
>.
Из того, что >
 >
- нормальная максимальная подгруппа в
группе >
>
- нормальная максимальная подгруппа в
группе >
 >,
следует, что >
>,
следует, что >
 >
- группа простого порядка >
>
- группа простого порядка >
 >.
>.
Покажем
теперь, что >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Пусть >
>.
Пусть >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Тогда >
>.
Тогда >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
для любого >
>
для любого >
 >.
По условию >
>.
По условию >
 >
- подгруппа группы >
>
- подгруппа группы >
 >.
Поскольку порядок
>.
Поскольку порядок
> >
>
делит >
 >,
то >
>,
то >
 >.
Таким образом >
>.
Таким образом >
 >
для любого >
>
для любого >
 >,
т.е. >
>,
т.е. >
 >.
Так как >
>.
Так как >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >,
то >
>,
то >
 >,
и поэтому >
>,
и поэтому >
 >.
Отсюда получаем, что >
>.
Отсюда получаем, что >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Поскольку >
>.
Поскольку >
 >
- >
>
- >
 >-максимальная
подгруппа, то согласно следствия, >
>-максимальная
подгруппа, то согласно следствия, >
 >
- нильпотентная группа, и поэтому >
>
- нильпотентная группа, и поэтому >
 >.
Это означает, что >
>.
Это означает, что >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Таким образом, группа >
>.
Таким образом, группа >
 >
является группой типа (7).
>
является группой типа (7).
Итак, >
 >
- группа одного из типов (1) - (7) теоремы.
>
- группа одного из типов (1) - (7) теоремы.
Достаточность.
Покажем, что в группе >
 >
каждая >
>
каждая >
 >-максимальная
подгруппа перестановочна со всеми
>
>-максимальная
подгруппа перестановочна со всеми
>
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >.
>.
Пусть >
 >
- группа типа (1) или (2). Ввиду леммы Error: Reference source not found,
в группе >
>
- группа типа (1) или (2). Ввиду леммы Error: Reference source not found,
в группе >
 >
каждая >
>
каждая >
 >-максимальная
подгруппа перестановочна со всеми
>
>-максимальная
подгруппа перестановочна со всеми
>
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >.
>.
Пусть >
 >
- группа типа (3). Тогда >
>
- группа типа (3). Тогда >
 >
и >
>
и >
 >,
где >
>,
где >
 >
- группа простого порядка >
>
- группа простого порядка >
 >,
>
>,
>
 >
- нециклическая группа и все ее максимальные
подгруппы, отличные от >
>
- нециклическая группа и все ее максимальные
подгруппы, отличные от >
 >,
цикличны. Пусть >
>,
цикличны. Пусть >
 >.
>.
Так как >
 >,
то >
>,
то >
 >,
и поэтому в группе >
>,
и поэтому в группе >
 >
существует нильпотентная максимальная
подгруппа, индекс которой равен >
>
существует нильпотентная максимальная
подгруппа, индекс которой равен >
 >.
Пусть >
>.
Пусть >
 >
- произвольная нильпотентная максимальная
подгруппа группы >
>
- произвольная нильпотентная максимальная
подгруппа группы >
 >
с индексом >
>
с индексом >
 >.
Тогда >
>.
Тогда >
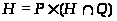 >.
Так как >
>.
Так как >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
то >
>,
то >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >,
и следовательно,
>,
и следовательно,
> >
>
Значит, >
 >
- единственная нильпотентная максимальная
подгруппа, индекс которой равен >
>
- единственная нильпотентная максимальная
подгруппа, индекс которой равен >
 >.
>.
Пусть >
 >
- произвольная максимальная подгруппа
в >
>
- произвольная максимальная подгруппа
в >
 >
и >
>
и >
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >.
Пусть >
>.
Пусть >
 >
- произвольная максимальная подгруппа
в >
>
- произвольная максимальная подгруппа
в >
 >,
>
>,
>
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >,
>
>,
>
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >.
>.
1. Если >
 >
и >
>
и >
 >
- нильпотентные подгруппы группы >
>
- нильпотентные подгруппы группы >
 >
индекса >
>
индекса >
 >,
то >
>,
то >
 >.
Так как >
>.
Так как >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
то >
>,
то >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >,
и следовательно, >
>,
и следовательно, >
 >
перестановочна с >
>
перестановочна с >
 >.
>.
2. Предположим,
что >
 >
является ненильпотентной подгруппой.
Так как >
>
является ненильпотентной подгруппой.
Так как >
 >,
то >
>,
то >
 >.
Из того, что >
>.
Из того, что >
 >,
следует, что >
>,
следует, что >
 >
- циклическая подгруппа. Так как >
>
- циклическая подгруппа. Так как >
 >,
то >
>,
то >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
и поэтому >
>,
и поэтому >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Из того, что >
>.
Из того, что >
 >,
следует, что >
>,
следует, что >
 >.
Следовательно, >
>.
Следовательно, >
 >
- нильпотентная максимальная подгруппа
группы >
>
- нильпотентная максимальная подгруппа
группы >
 >,
индекс которой равен >
>,
индекс которой равен >
 >.
Если >
>.
Если >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
такая, что >
>
такая, что >
 >,
то >
>,
то >
 >
- >
>
- >
 >-подгруппа,
и поэтому >
>-подгруппа,
и поэтому >
 >
- нильпотентная подгруппа. Пусть >
>
- нильпотентная подгруппа. Пусть >
 >
- произвольная максимльная подгруппа
группы >
>
- произвольная максимльная подгруппа
группы >
 >,
индекс которой >
>,
индекс которой >
 >
равен >
>
равен >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >.
Следовательно, для некоторого >
>.
Следовательно, для некоторого >
 >
мы имеем >
>
мы имеем >
 >.
Без ограничения общности можно полагать,
что >
>.
Без ограничения общности можно полагать,
что >
 >.
Так как >
>.
Так как >
 >
- максимальная подгруппа циклической
группы >
>
- максимальная подгруппа циклической
группы >
 >,
то >
>,
то >
 >,
и поэтому >
>,
и поэтому >
 >
- нильпотентная максимальная подгруппа.
Следовательно, >
>
- нильпотентная максимальная подгруппа.
Следовательно, >
 >
- группа Шмидта. Значит, >
>
- группа Шмидта. Значит, >
 >
и поэтому >
>
и поэтому >
 >,
где >
>,
где >
 >
- циклическая >
>
- циклическая >
 >-подгруппа.
>-подгруппа.
Если >
 >,
то >
>,
то >
 >.
Так как >
>.
Так как >
 >
- подгруппа циклической группы >
>
- подгруппа циклической группы >
 >,
то >
>,
то >
 >.
Из того, что >
>.
Из того, что >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
следует, что >
>,
следует, что >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >
и поэтому >
>
и поэтому >
 >.
Это означает, что подгруппа >
>.
Это означает, что подгруппа >
 >
перестановочна со всеми 2-максимальными
подгруппами группы >
>
перестановочна со всеми 2-максимальными
подгруппами группы >
 >.
>.
Если >
 >,
то >
>,
то >
 >
- подгруппа циклической группы >
>
- подгруппа циклической группы >
 >
и поэтому >
>
и поэтому >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Так как группа >
>.
Так как группа >
 >
нильпотентна, то >
>
нильпотентна, то >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >
и поэтому >
>
и поэтому >
 >
перестановочна со всеми 2-максимальными
подгруппами группы >
>
перестановочна со всеми 2-максимальными
подгруппами группы >
 >.
>.
3. Предположим
теперь, что >
 >
- нильпотентная группа, такая что >
>
- нильпотентная группа, такая что >
 >,
и >
>,
и >
 >
не является нильпотентнай подгруппой.
Тогда >
>
не является нильпотентнай подгруппой.
Тогда >
 >.
Рассуждая как выше видим, что >
>.
Рассуждая как выше видим, что >
 >
- группа Шмидта. Так как >
>
- группа Шмидта. Так как >
 >,
то >
>,
то >
 >
имеет вид
>
имеет вид
> >,
>,
где >
 >
- циклическая >
>
- циклическая >
 >-группа.
>-группа.
Если >
 >,
то >
>,
то >
 >.
Но >
>.
Но >
 >
- подгруппа циклической группы >
>
- подгруппа циклической группы >
 >
и поэтому >
>
и поэтому >
 >.
Из того, что >
>.
Из того, что >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
следует, что >
>,
следует, что >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >
и поэтому мы имеем >
>
и поэтому мы имеем >
 >,
что влечет перестановочность подгруппы
>
>,
что влечет перестановочность подгруппы
>
 >
со всеми >
>
со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >,
в частности с >
>,
в частности с >
 >.
>.
Если >
 >,
то подгруппа >
>,
то подгруппа >
 >
содержится в некоторой силовской
>
>
содержится в некоторой силовской
>
 >-подгруппе
>
>-подгруппе
>
 >
группы >
>
группы >
 >.
Так как >
>.
Так как >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
то >
>,
то >
 >
и поэтому >
>
и поэтому >
 >.
Следовательно, >
>.
Следовательно, >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Значит, >
>.
Значит, >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Так как >
>.
Так как >
 >
- нильпотентная группа, такая что >
>
- нильпотентная группа, такая что >
 >,
то >
>,
то >
 >.
Ясно, что >
>.
Ясно, что >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >
имеет вид >
>
имеет вид >
 >.
Так как >
>.
Так как >
 >,
то имеет место >
>,
то имеет место >
 >
и поэтому
>
и поэтому
> >.
>.
Это означает,
что подгруппы >
 >
и >
>
и >
 >
перестановочны. Если >
>
перестановочны. Если >
 >,
то >
>,
то >
 >
и поэтому >
>
и поэтому >
 >.
Следовательно, подгруппы >
>.
Следовательно, подгруппы >
 >
и >
>
и >
 >
перестановочны.
>
перестановочны.
4. Если >
 >,
то подгруппа >
>,
то подгруппа >
 >
является максимальной подгруппой группы
>
>
является максимальной подгруппой группы
>
 >
индекса >
>
индекса >
 >
и >
>
и >
 >
- 2-максимальная подгруппа в >
>
- 2-максимальная подгруппа в >
 >.
Но подгруппы такого вида уже изучены.
>.
Но подгруппы такого вида уже изучены.
5. Если >
 >,
то подгруппа >
>,
то подгруппа >
 >
является максимальной подгруппой группы
>
>
является максимальной подгруппой группы
>
 >
с индексом >
>
с индексом >
 >
и >
>
и >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Но как мы уже знаем, максимальные
подгруппы >
>.
Но как мы уже знаем, максимальные
подгруппы >
 >
группы >
>
группы >
 >
перестановочны со всеми >
>
перестановочны со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >.
>.
Это означает,
что в любом случае >
 >
перестановочна со всеми >
>
перестановочна со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >.
>.
Легко видеть,
что в группе >
 >
типа (4) каждая >
>
типа (4) каждая >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
перестановочна со всеми >
>
перестановочна со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >.
>.
Пусть >
 >
- группа типа (5). Легко видеть, что в
группе >
>
- группа типа (5). Легко видеть, что в
группе >
 >
все >
>
все >
 >-максимальные
подгруппы группы >
>-максимальные
подгруппы группы >
 >
нормальны в группе >
>
нормальны в группе >
 >.
Таким образом, каждая >
>.
Таким образом, каждая >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
перестановочна со всеми >
>
перестановочна со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >.
>.
Пусть >
 >
- группа типа (6). Пусть >
>
- группа типа (6). Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Понятно, что либо >
>.
Понятно, что либо >
 >,
либо >
>,
либо >
 >,
где >
>,
где >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >
- единственная неединичная >
>
- единственная неединичная >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >,
и поэтому подгруппа >
>,
и поэтому подгруппа >
 >
перестановочна со всеми >
>
перестановочна со всеми >
 >-максимальнаыми
подгруппами группы >
>-максимальнаыми
подгруппами группы >
 >.
>.
Пусть >
 >
- группа типа (7). Тогда >
>
- группа типа (7). Тогда >
 >,
где >
>,
где >
 >
- подгруппа группы >
>
- подгруппа группы >
 >
простого порядка >
>
простого порядка >
 >,
>
>,
>
 >
- подгруппа группы >
>
- подгруппа группы >
 >
простого порядка >
>
простого порядка >
 >
и >
>
и >
 >
- циклическая >
>
- циклическая >
 >-подгруппа
группы >
>-подгруппа
группы >
 >,
которая не является нормальной подгруппой
в группе >
>,
которая не является нормальной подгруппой
в группе >
 >,
но максимальная подгруппа группы >
>,
но максимальная подгруппа группы >
 >
нормальна в >
>
нормальна в >
 >.
Покажем, что в группе >
>.
Покажем, что в группе >
 >
любая >
>
любая >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
перестановочна со всеми >
>
перестановочна со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >.
Предположим, что данное утверждение не
верно, и пусть >
>.
Предположим, что данное утверждение не
верно, и пусть >
 >
- контрпример минимального порядка.
>
- контрпример минимального порядка.
Предположим,
что >
 >.
Пусть >
>.
Пусть >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Понятно, что >
>.
Понятно, что >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >.
Следовательно, >
>.
Следовательно, >
 >
перестановочна с любой >
>
перестановочна с любой >
 >-максимальной
подгруппой группы >
>-максимальной
подгруппой группы >
 >.
Полученное противоречие с выбором
группы >
>.
Полученное противоречие с выбором
группы >
 >
показывает, что >
>
показывает, что >
 >.
>.
Пусть >
 >
- подгруппа группы >
>
- подгруппа группы >
 >
с индексом >
>
с индексом >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- неединичная подгруппа группы >
>
- неединичная подгруппа группы >
 >.
Ясно, что >
>.
Ясно, что >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >.
Факторгруппа >
>.
Факторгруппа >
 >
имеет вид >
>
имеет вид >
 >,
где >
>,
где >
 >
- силовская подгруппа порядка >
>
- силовская подгруппа порядка >
 >,
>
>,
>
 >
- силовская подгруппа порядка >
>
- силовская подгруппа порядка >
 >,
>
>,
>
 >
- циклическая силовская >
>
- циклическая силовская >
 >-подгруппа,
которая не является нормальной подгруппой
в >
>-подгруппа,
которая не является нормальной подгруппой
в >
 >,
но максимальная подгруппа >
>,
но максимальная подгруппа >
 >
группы >
>
группы >
 >
нормальна в группе >
>
нормальна в группе >
 >.
Поскольку >
>.
Поскольку >
 >,
то >
>,
то >
 >
и поэтому по выбору группы >
>
и поэтому по выбору группы >
 >
мы заключаем, что любая >
>
мы заключаем, что любая >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
перестановочна со всеми >
>
перестановочна со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >.
Пусть >
>.
Пусть >
 >
- произвольная >
>
- произвольная >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
и >
>
и >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Понятно, что >
>.
Понятно, что >
 >
и >
>
и >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
и >
>
и >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >,
и поэтому
>,
и поэтому
> >
>
Следовательно,
подгруппы >
 >
и >
>
и >
 >
перестановочны. Полученное противоречие
с выбором группы >
>
перестановочны. Полученное противоречие
с выбором группы >
 >
заканчивает доказательство теоремы.
>
заканчивает доказательство теоремы.
Если в
группе >
 >
любая ее >
>
любая ее >
 >-максимальная
подгруппа перестановочна со всеми
>
>-максимальная
подгруппа перестановочна со всеми
>
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >
и >
>
и >
 >,
то >
>,
то >
 >
- нильпотентная группа.
>
- нильпотентная группа.
Классы групп типов (1) -(7), очевидно, попарно не пересекаются. Покажем, что все это классы не пусты. Но фактически мы должны установить это лишь для классов (2), (3), (5) - (7).
Хорошо
известно, что в группе автоморфизмов >
 >
группы кватернионов >
>
группы кватернионов >
 >
имеется элемент >
>
имеется элемент >
 >
порядка >
>
порядка >
 >.
Пусть >
>.
Пусть >
 >.
Тогда >
>.
Тогда >
 >
принадлежит типу (2). Действительно,
пусть >
>
принадлежит типу (2). Действительно,
пусть >
 >
- единственная подгруппа порядка 2 группы
>
>
- единственная подгруппа порядка 2 группы
>
 >.
Тогда >
>.
Тогда >
 >
и поэтому >
>
и поэтому >
 >.
Понятно, что >
>.
Понятно, что >
 >
- главный фактор группы >
>
- главный фактор группы >
 >
и кроме того, >
>
и кроме того, >
 >.
Таким образом, >
>.
Таким образом, >
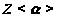 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
и все максимальные в >
>
и все максимальные в >
 >
подгруппы, индекс которых делится на
2, сопряжены с >
>
подгруппы, индекс которых делится на
2, сопряжены с >
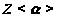 >.
Следовательно, >
>.
Следовательно, >
 >
- группа Шмидта.
>
- группа Шмидта.
Пусть
> >
>
и >
 >
- группа порядка 7. Ввиду леммы Error: Reference source not found,
>
>
- группа порядка 7. Ввиду леммы Error: Reference source not found,
>
 >
- абелева группа порядка 9. Поскольку >
>
- абелева группа порядка 9. Поскольку >
 >
изоморфна некоторой подгруппе >
>
изоморфна некоторой подгруппе >
 >
порядка 3 из группы автоморфизмов >
>
порядка 3 из группы автоморфизмов >
 >,
то >
>,
то >
 >
- группа операторов для >
>
- группа операторов для >
 >
с >
>
с >
 >.
Пусть >
>.
Пусть >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
и >
>
и >
 >
не является нормальной подгруппой
группы >
>
не является нормальной подгруппой
группы >
 >.
Легко проверить, что все максимальные
подгруппы группы >
>.
Легко проверить, что все максимальные
подгруппы группы >
 >,
отличные от >
>,
отличные от >
 >,
цикличны и не являются нормальными
подгруппами группы >
>,
цикличны и не являются нормальными
подгруппами группы >
 >
и поэтому >
>
и поэтому >
 >
- группа типа (3).
>
- группа типа (3).
Пусть теперь
>
 >
и >
>
и >
 >
- такие простые числа, что >
>
- такие простые числа, что >
 >
делит >
>
делит >
 >.
Тогда если >
>.
Тогда если >
 >
- группа порядка >
>
- группа порядка >
 >,
то в группе ее автоморфизмов >
>,
то в группе ее автоморфизмов >
 >
имеется подгруппа >
>
имеется подгруппа >
 >
порядка >
>
порядка >
 >.
Пусть >
>.
Пусть >
 >,
где >
>,
где >
 >
- группа порядка >
>
- группа порядка >
 >.
Тогда >
>.
Тогда >
 >
- группа операторов для >
>
- группа операторов для >
 >
с >
>
с >
 >
и поэтому группа >
>
и поэтому группа >
 >
принадлежит типу (3).
>
принадлежит типу (3).
Пусть снова
>
 >
и >
>
и >
 >
- группы, введенные в примере, >
>
- группы, введенные в примере, >
 >
и >
>
и >
 >,
где >
>,
где >
 >
Пусть >
>
Пусть >
 >
- канонический эпиморфизм группы >
>
- канонический эпиморфизм группы >
 >
на факторгруппу >
>
на факторгруппу >
 >.
Пусть >
>.
Пусть >
 >
- прямое произведение групп >
>
- прямое произведение групп >
 >
и >
>
и >
 >
с объединенной факторгруппой >
>
с объединенной факторгруппой >
 >
(см. лемму Error: Reference source not found). Пусть >
>
(см. лемму Error: Reference source not found). Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >.
Тогда >
>.
Тогда >
 >,
где >
>,
где >
 >
и поэтому
>
и поэтому
> >,
где >
>,
где >
 >
>
>
>
 >
>
Покажем, что
>
 >.
Поскольку >
>.
Поскольку >
 >
и >
>
и >
 >,
то >
>,
то >
 >.
Следовательно, >
>.
Следовательно, >
 >
и поэтому >
>
и поэтому >
 >.
Значит, >
>.
Значит, >
 >.
Так как >
>.
Так как >
 >
и >
>
и >
 >,
то >
>,
то >
 >
и поэтому >
>
и поэтому >
 >
. Пусть >
>
. Пусть >
 >
- неединичная подгруппа из >
>
- неединичная подгруппа из >
 >.
Ясно, что >
>.
Ясно, что >
 >.
Пусть >
>.
Пусть >
 >.
Мы имеем
>.
Мы имеем
> >
>
Значит, >
 >
и поэтому >
>
и поэтому >
 >.
Следовательно, >
>.
Следовательно, >
 >
- нормальная погруппа в >
>
- нормальная погруппа в >
 >.
Таким образом, группа >
>.
Таким образом, группа >
 >
принадлежит типу (5).
>
принадлежит типу (5).
Пусть >
 >
- циклическая группа порядка >
>
- циклическая группа порядка >
 >,
где >
>,
где >
 >
- простое нечетное число. Согласно лемме
Error: Reference source not found, >
>
- простое нечетное число. Согласно лемме
Error: Reference source not found, >
 >.
Пусть теперь >
>.
Пусть теперь >
 >
- произвольный простой делитель числа
>
>
- произвольный простой делитель числа
>
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >
в >
>
в >
 >.
Обозначим символом >
>.
Обозначим символом >
 >
полупрямое произведение >
>
полупрямое произведение >
 >.
Пусть >
>.
Пусть >
 >
- подгруппа порядка >
>
- подгруппа порядка >
 >
группы >
>
группы >
 >.
Тогда >
>.
Тогда >
 >
и поэтому если >
>
и поэтому если >
 >,
то согласно лемме Error: Reference source not found,
>
>,
то согласно лемме Error: Reference source not found,
>
 >,
что противоречит определению группы
>
>,
что противоречит определению группы
>
 >.
Следовательно, >
>.
Следовательно, >
 >,
что влечет >
>,
что влечет >
 >.
Значит, группа >
>.
Значит, группа >
 >
принадлежит типу(6).
>
принадлежит типу(6).
Покажем,
наконец, что класс групп (7) не пуст. Пусть
>
 >
и >
>
и >
 >
- группы нечетных простых порядков >
>
- группы нечетных простых порядков >
 >
и >
>
и >
 >
соответственно (>
>
соответственно (> >).
Тогда
>).
Тогда
> >
>
и поэтому
найдется такой простой делитель >
 >
числа >
>
числа >
 >,
который одновременно отличен от >
>,
который одновременно отличен от >
 >
и >
>
и >
 >.
Пусть >
>.
Пусть >
 >,
где >
>,
где >
 >
- группа порядка >
>
- группа порядка >
 >
в >
>
в >
 >.
Тогда группа >
>.
Тогда группа >
 >
принадлежит типу (7).
>
принадлежит типу (7).
4.
Группы, в которых максимальные подгруппы
перестановочны с >
 >-максимальными
подгруппами
>-максимальными
подгруппами
В данном
разделе дано описание групп, у которых
каждая максимальная подгруппа группы
перестановочна со всеми ее >
 >-максимальными
подгруппами.
>-максимальными
подгруппами.
Для доказательства основного результата данного раздела нам понадобятся следующие леммы.
Класс >
 >
всех таких абелевых групп >
>
всех таких абелевых групп >
 >,что
>
>,что
>
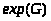 >
не содержит кубов, является формацией.
>
не содержит кубов, является формацией.
Доказательство.
Пусть >
 >.
И пусть >
>.
И пусть >
 >
- произвольная нормальная подгруппа
группы >
>
- произвольная нормальная подгруппа
группы >
 >.
Тогда >
>.
Тогда >
 >
абелева. Так как по определению экспоненты
>
>
абелева. Так как по определению экспоненты
>
 >
делит >
>
делит >
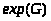 >
и поскольку >
>
и поскольку >
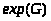 >
не содержит кубов, то >
>
не содержит кубов, то >
 >
не содержит кубов. Следовательно, >
>
не содержит кубов. Следовательно, >
 >.
>.
Пусть >
 >
и >
>
и >
 >.
Покажем, что
>.
Покажем, что
> >.
>.
Пусть >
 >.
Тогда >
>.
Тогда >
 >,
где >
>,
где >
 >
и >
>
и >
 >.
Так как >
>.
Так как >
 >,
то по определению экспоненты >
>,
то по определению экспоненты >
 >.
Из того, что >
>.
Из того, что >
 >
и >
>
и >
 >
не содержат кубов, следует, что >
>
не содержат кубов, следует, что >
 >
не содержит кубов. Поскольку группа >
>
не содержит кубов. Поскольку группа >
 >
изоморфна подгруппе из >
>
изоморфна подгруппе из >
 >,
то >
>,
то >
 >
делит >
>
делит >
 >,
и поэтому >
>,
и поэтому >
 >
не содержит кубов. Так как группа >
>
не содержит кубов. Так как группа >
 >
абелева, то >
>
абелева, то >
 >.
Следовательно, >
>.
Следовательно, >
 >
- формация. Лемма доказана.
>
- формация. Лемма доказана.
[4.1]. Пусть
>
 >,
где >
>,
где >
 >
- формация, описанная в лемме. Если каждая
максимальная подгруппа группы >
>
- формация, описанная в лемме. Если каждая
максимальная подгруппа группы >
 >
перестановочна с любой >
>
перестановочна с любой >
 >-максимальной
подгруппой группы >
>-максимальной
подгруппой группы >
 >,
то >
>,
то >
 >.
>.
Доказательство.
Предположим, что лемма не верна, и пусть
>
 >
- контрпример минимального порядка.
Доказательство разобьем на следующие
этапы.
>
- контрпример минимального порядка.
Доказательство разобьем на следующие
этапы.
(1) Для любой
неединичной нормальной подгруппы >
 >
группы >
>
группы >
 >,
факторгруппа >
>,
факторгруппа >
 >.
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
и >
>
и >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Тогда >
>.
Тогда >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
и >
>
и >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Из того, что по условию подгруппы >
>.
Из того, что по условию подгруппы >
 >
и >
>
и >
 >
перестановочны, мы имеем
>
перестановочны, мы имеем
> >
>
Поскольку
>
 >,
то >
>,
то >
 >
и поэтому по выбору группы >
>
и поэтому по выбору группы >
 >
мы заключаем, что >
>
мы заключаем, что >
 >.
>.
(2) >
 >
имеет единственную минимальную нормальную
подгруппу >
>
имеет единственную минимальную нормальную
подгруппу >
 >
для некоторого простого >
>
для некоторого простого >
 >,
и >
>,
и >
 >
где >
>
где >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
с >
>
с >
 >.
>.
Пусть >
 >
- минимальная нормальная подгруппа
группы >
>
- минимальная нормальная подгруппа
группы >
 >.
Ввиду леммы, >
>.
Ввиду леммы, >
 >
- разрешимая группа, и поэтому >
>
- разрешимая группа, и поэтому >
 >
- элементарная абелева >
>
- элементарная абелева >
 >-группа
для некоторого простого >
>-группа
для некоторого простого >
 >.
Так как >
>.
Так как >
 >
- насыщенная формация , то ввиду (1), >
>
- насыщенная формация , то ввиду (1), >
 >
- единственная минимальная нормальная
подгруппа группы >
>
- единственная минимальная нормальная
подгруппа группы >
 >
и >
>
и >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
не содержащая >
>,
не содержащая >
 >
и >
>
и >
 >.
По тождеству Дедекинда, мы имеем >
>.
По тождеству Дедекинда, мы имеем >
 >.
Из того, что >
>.
Из того, что >
 >
абелева, следует, что >
>
абелева, следует, что >
 >
и поэтому >
>
и поэтому >
 >.
Это показывает, что >
>.
Это показывает, что >
 >,
>
>,
>
 >.
>.
(3) Заключительное противоречие.
Ввиду (2), для
некоторой максимальной подгруппы >
 >
группы >
>
группы >
 >
имеем >
>
имеем >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >.
Пусть >
>.
Пусть >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Тогда по условию, >
>.
Тогда по условию, >
 >
для каждого >
>
для каждого >
 >.
По лемме Error: Reference source not found, >
>.
По лемме Error: Reference source not found, >
 >
и поэтому >
>
и поэтому >
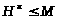 >.
Следовательно, >
>.
Следовательно, >
 >.
Это означает, что каждая >
>.
Это означает, что каждая >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >
единичная, и следовательно, >
>
единичная, и следовательно, >
 >
- простое число для всех максимальных
подгруппы >
>
- простое число для всех максимальных
подгруппы >
 >
группы >
>
группы >
 >.
Так как >
>.
Так как >
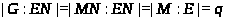 >
для некоторого простого >
>
для некоторого простого >
 >,
то >
>,
то >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Это означает, что >
>.
Это означает, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
>.
Предположим,
что >
 >.
Тогда в >
>.
Тогда в >
 >
имеется неединичная максимальная
подгруппа >
>
имеется неединичная максимальная
подгруппа >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >,
и поэтому >
>,
и поэтому >
 >
перестановочна с >
>
перестановочна с >
 >.
Следовательно, >
>.
Следовательно, >
 >,
но >
>,
но >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >.
>.
Поскольку ввиду (1),
> >,
то >
>,
то >
 >
- нильпотентная подгруппа.
>
- нильпотентная подгруппа.
Из того, что
>
 >
- неединичная нормальная подгруппа в
группе >
>
- неединичная нормальная подгруппа в
группе >
 >,
следует, что >
>,
следует, что >
 >.
>.
Так как
факторгруппа >
 >
изоморфна подгруппе группы автоморфизмов
>
>
изоморфна подгруппе группы автоморфизмов
>
 >
и группа автоморфизмов >
>
и группа автоморфизмов >
 >
группы >
>
группы >
 >
простого порядка >
>
простого порядка >
 >
является циклической группой порядка
>
>
является циклической группой порядка
>
 >,
то >
>,
то >
 >
абелева. Из того, что >
>
абелева. Из того, что >
 >
и >
>
и >
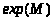 >
не содержит кубов, следует, что >
>
не содержит кубов, следует, что >
 >
не содержит кубов. Это означает, что >
>
не содержит кубов. Это означает, что >
 >.
Следовательно, >
>.
Следовательно, >
 >,
и поэтому >
>,
и поэтому >
 >
- нильпотентная подгруппа. Таким образом,
>
>
- нильпотентная подгруппа. Таким образом,
>
 >.
Полученное противоречие с выбором
группы >
>.
Полученное противоречие с выбором
группы >
 >
доказывает лемму.
>
доказывает лемму.
[4.1]. В
примитивной группе >
 >
каждая максимальная подгруппа группы
>
>
каждая максимальная подгруппа группы
>
 >
перестановочна со всеми >
>
перестановочна со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >
тогда и только тогда, когда группа >
>
тогда и только тогда, когда группа >
 >
имеет вид:
>
имеет вид:
(1) >
 >,
>,
где >
 >
- группа порядка >
>
- группа порядка >
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >,
где >
>,
где >
 >;
>;
(2) >
 >,
>,
где >
 >
- минимальная нормальная подгруппа в >
>
- минимальная нормальная подгруппа в >
 >
порядка >
>
порядка >
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >,
где >
>,
где >
 >;
>;
(3) >
 >,
>,
где >
 >
- группа порядка >
>
- группа порядка >
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >,
где >
>,
где >
 >.
>.
(4) >
 >,
>,
где >
 >
- группа порядка >
>
- группа порядка >
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >,
где >
>,
где >
 >
- различные простые делители порядка
группы >
>
- различные простые делители порядка
группы >
 >.
>.
Доказательство.
Необходимость. Так как ввиду теоремы,
группа >
 >
разрешима, то >
>
разрешима, то >
 >,
где >
>,
где >
 >
- примитиватор группы >
>
- примитиватор группы >
 >
и >
>
и >
 >
- единственная минимальная нормальная
подгруппа группы >
>
- единственная минимальная нормальная
подгруппа группы >
 >,
>
>,
>
 >.
Ввиду леммы Error: Reference source not found, >
>.
Ввиду леммы Error: Reference source not found, >
 >.
>.
Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >
и >
>
и >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
По условию подгруппы >
>.
По условию подгруппы >
 >
и >
>
и >
 >
перестановочны. Следовательно, для
любого >
>
перестановочны. Следовательно, для
любого >
 >,
>
>,
>
 >
- подгруппа группы >
>
- подгруппа группы >
 >,
и поэтому либо >
>,
и поэтому либо >
 >,
либо >
>,
либо >
 >.
Ввиду леммы, первый случай не возможен.
Следовательно, >
>.
Ввиду леммы, первый случай не возможен.
Следовательно, >
 >.
Это означает, что >
>.
Это означает, что >
 >
для любого >
>
для любого >
 >.
Значит, >
>.
Значит, >
 >.
Следовательно, в группе >
>.
Следовательно, в группе >
 >
все >
>
все >
 >-максимальные
подгруппы единичны. Это означает, что
либо >
>-максимальные
подгруппы единичны. Это означает, что
либо >
 >,
либо >
>,
либо >
 >,
либо >
>,
либо >
 >.
>.
1. Пусть >
 >.
Если >
>.
Если >
 >,
то группа >
>,
то группа >
 >
принадлежит типу (1). Если >
>
принадлежит типу (1). Если >
 >,
то группа >
>,
то группа >
 >
принадлежит типу (3).
>
принадлежит типу (3).
2. Пусть >
 >.
Допустим, что >
>.
Допустим, что >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Тогда >
>.
Тогда >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
По условию подгруппы >
>.
По условию подгруппы >
 >
и >
>
и >
 >
перестановочны. Следовательно, >
>
перестановочны. Следовательно, >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >.
В этом случае >
>.
В этом случае >
 >
- группа типа (2).
>
- группа типа (2).
3. Пусть >
 >.
Рассуждая как выше, видим, что >
>.
Рассуждая как выше, видим, что >
 >.
Значит, >
>.
Значит, >
 >
- группа типа (4).
>
- группа типа (4).
Достаточность очевидна. Лемма доказана.
Поскольку в
любой нильпотентной группе максимальная
подгруппа нормальна, то все они
перестановочны со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >.
Опишем теперь ненильпотентные группы,
у которых каждая максимальная подгруппа
перестановочна со всеми >
>.
Опишем теперь ненильпотентные группы,
у которых каждая максимальная подгруппа
перестановочна со всеми >
 >-максимальными
подруппами.
>-максимальными
подруппами.
[4.2]. В
ненильпотентной группе >
 >
каждая ее максимальная подгруппа
перестановочна со всеми >
>
каждая ее максимальная подгруппа
перестановочна со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >
тогда и только тогда, когда либо >
>
тогда и только тогда, когда либо >
 >
где >
>
где >
 >
- различные простые числа и >
>
- различные простые числа и >
 >
либо >
>
либо >
 >
- группа типа (2) из теоремы Error: Reference source not found,
либо >
>
- группа типа (2) из теоремы Error: Reference source not found,
либо >
 >
- сверхразрешимая группа одного из
следующих типов:
>
- сверхразрешимая группа одного из
следующих типов:
(1) >
 >,
>,
где >
 >
- группа простого порядка >
>
- группа простого порядка >
 >,
а >
>,
а >
 >
- такая бипримарная группа с циклическими
силовскими подгруппами, что >
>
- такая бипримарная группа с циклическими
силовскими подгруппами, что >
 >,
где >
>,
где >
 >
и >
>
и >
 >;
>;
(2) >
 >,
>,
где >
 >
- группа простого порядка >
>
- группа простого порядка >
 >,
>
>,
>
 >
- циклическая >
>
- циклическая >
 >-группа
с >
>-группа
с >
 >
(>
>
(> >)
и >
>)
и >
 >;
>;
(3) >
 >,
>,
где >
 >
- группа простого порядка >
>
- группа простого порядка >
 >,
>
>,
>
 >
- >
>
- >
 >-группа
с >
>-группа
с >
 >
(>
>
(> >),
>
>),
>
 >
и все максимальные подгруппы в >
>
и все максимальные подгруппы в >
 >,
отличные от >
>,
отличные от >
 >,
цикличны.
>,
цикличны.
Доказательство. Необходимость.
Пусть >
 >
- группа, в которой каждая максимальная
подгруппа перестановочна с любой
>
>
- группа, в которой каждая максимальная
подгруппа перестановочна с любой
>
 >-максимальной
подгруппой группы >
>-максимальной
подгруппой группы >
 >.
>.
Поскольку >
 >
- ненильпотентная группа, то в ней
существует максимальная подгруппа >
>
- ненильпотентная группа, то в ней
существует максимальная подгруппа >
 >,
которая не является нормальной в >
>,
которая не является нормальной в >
 >.
Тогда >
>.
Тогда >
 >.
Следовательно, >
>.
Следовательно, >
 >
- примитивная группа, которая удовлетворяет
условиям леммы Error: Reference source not found.
>
- примитивная группа, которая удовлетворяет
условиям леммы Error: Reference source not found.
I. Пусть >
 >,
где >
>,
где >
 >
и >
>
и >
 >
- простые числа (не обязательно различные).
Ввиду леммы Error: Reference source not found, >
>
- простые числа (не обязательно различные).
Ввиду леммы Error: Reference source not found, >
 >
и >
>
и >
 >.
>.
Так как >
 >,
то >
>,
то >
 >
содержится в некоторой максимальной
подгруппе >
>
содержится в некоторой максимальной
подгруппе >
 >
группы >
>
группы >
 >.
Пусть >
>.
Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >
и >
>
и >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Следовательно, для любого >
>.
Следовательно, для любого >
 >
подгруппы >
>
подгруппы >
 >
и >
>
и >
 >
перестановочны. Это означает, что >
>
перестановочны. Это означает, что >
 >.
Поскольку >
>.
Поскольку >
 >,
то либо >
>,
то либо >
 >,
либо >
>,
либо >
 >.
Ясно, что первый случай не возможен.
Следовательно, >
>.
Ясно, что первый случай не возможен.
Следовательно, >
 >
- единственная максимальная подгруппа
группы >
>
- единственная максимальная подгруппа
группы >
 >,
и поэтому >
>,
и поэтому >
 >
- примарная циклическая группа. Ввиду
произвольного выбора >
>
- примарная циклическая группа. Ввиду
произвольного выбора >
 >,
>
>,
>
 >
- примарная циклическая группа.
>
- примарная циклическая группа.
Пусть >
 >.
Тогда >
>.
Тогда >
 >
для некоторого >
>
для некоторого >
 >.
Пусть >
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >,
>
>,
>
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >
и >
>
и >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >.
Так как
>.
Так как
> >,
>,
то >
 >
- группа порядка >
>
- группа порядка >
 >
и >
>
и >
 >.
Из того, что факторгруппа >
>.
Из того, что факторгруппа >
 >
сверхразрешима и подгруппа >
>
сверхразрешима и подгруппа >
 >
циклическая, следует, что >
>
циклическая, следует, что >
 >
- сверхразрешимая группа. Допустим, что
>
>
- сверхразрешимая группа. Допустим, что
>
 >
- наибольший простой делитель порядка
группы >
>
- наибольший простой делитель порядка
группы >
 >.
Тогда >
>.
Тогда >
 >
и поэтому >
>
и поэтому >
 >.
Значит, >
>.
Значит, >
 >
и >
>
и >
 >,
противоречие. Если >
>,
противоречие. Если >
 >
- наибольший простой делитель порядка
группы >
>
- наибольший простой делитель порядка
группы >
 >,
то рассуждая как выше видим, что >
>,
то рассуждая как выше видим, что >
 >
и >
>
и >
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >
- наибольший простой делитель порядка
группы >
>
- наибольший простой делитель порядка
группы >
 >.
Значит, >
>.
Значит, >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >
и >
>
и >
 >,
где >
>,
где >
 >
- группа порядка >
>
- группа порядка >
 >,
>
>,
>
 >
- >
>
- >
 >-группа.
Ясно, что >
>-группа.
Ясно, что >
 >
- единственная >
>
- единственная >
 >-максимальная
подгруппа в >
>-максимальная
подгруппа в >
 >.
Поскольку >
>.
Поскольку >
 >
- неприводимая абелева группа автоморфизмов
группы >
>
- неприводимая абелева группа автоморфизмов
группы >
 >,
то >
>,
то >
 >
- циклическая группа и поэтому >
>
- циклическая группа и поэтому >
 >
- циклическая группа. Следовательно, >
>
- циклическая группа. Следовательно, >
 >
- группа типа (2).
>
- группа типа (2).
Пусть теперь
>
 >.
Поскольку в группе >
>.
Поскольку в группе >
 >
все максимальные подгруппы примарны и
цикличны, то >
>
все максимальные подгруппы примарны и
цикличны, то >
 >
и поэтому >
>
и поэтому >
 >.
>.
II. Пусть >
 >.
Согласно лемме Error: Reference source not found, >
>.
Согласно лемме Error: Reference source not found, >
 >,
где >
>,
где >
 >
- минимальная нормальная подгруппа в
группе >
>
- минимальная нормальная подгруппа в
группе >
 >
и либо >
>
и либо >
 >,
либо >
>,
либо >
 >.
>.
1. Пусть >
 >.
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >.
>.
Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >,
отличная от >
>,
отличная от >
 >.
Рассуждая как выше видим, что >
>.
Рассуждая как выше видим, что >
 >
- примарная циклическая группа. Значит,
>
>
- примарная циклическая группа. Значит,
>
 >.
>.
Предположим,
что >
 >
- >
>
- >
 >-группа.
Тогда >
>-группа.
Тогда >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
>.
Допустим,
что >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
такая, что >
>
такая, что >
 >.
Тогда >
>.
Тогда >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >,
и следовательно, >
>,
и следовательно, >
 >
- подгруппа группы >
>
- подгруппа группы >
 >,
что влечет
>,
что влечет
> >
>
Полученное
противоречие показывает, что >
 >
и поэтому >
>
и поэтому >
 >.
Значит, >
>.
Значит, >
 >,
где >
>,
где >
 >
- минимальная нормальная подгруппа
группы >
>
- минимальная нормальная подгруппа
группы >
 >
порядка >
>
порядка >
 >
и >
>
и >
 >.
Следовательно, >
>.
Следовательно, >
 >.
>.
Пусть теперь
>
 >
и >
>
и >
 >.
Пусть >
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
в >
>-подгруппа
в >
 >
и >
>
и >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
которая содержит >
>,
которая содержит >
 >.
Тогда >
>.
Тогда >
 >.
>.
Так как >
 >
- циклическая силовская >
>
- циклическая силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >,
то >
>,
то >
 >
- >
>
- >
 >-сверхразрешимая
группа.
>-сверхразрешимая
группа.
Предположим,
что >
 >.
Пусть >
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >
и пусть >
>
и пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Тогда >
>.
Тогда >
 >.
Допустим, что >
>.
Допустим, что >
 >.
Тогда ввиду леммы Error: Reference source not found, >
>.
Тогда ввиду леммы Error: Reference source not found, >
 >
- сверхразрешимая группа, >
>
- сверхразрешимая группа, >
 >
и поэтому >
>
и поэтому >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Пусть >
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >.
Так как >
>.
Так как >
 >
- нормальная максимальная подгруппа в
группе >
>
- нормальная максимальная подгруппа в
группе >
 >,
то >
>,
то >
 >.
Поскольку >
>.
Поскольку >
 >
сверхразрешима, то >
>
сверхразрешима, то >
 >,
и поэтому >
>,
и поэтому >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Из того, что >
>.
Из того, что >
 >
- циклическая группа, следует, что >
>
- циклическая группа, следует, что >
 >.
Значит, >
>.
Значит, >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Предположим, что >
>.
Предположим, что >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
такая что >
>,
такая что >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Поскольку по условию подгруппы >
>.
Поскольку по условию подгруппы >
 >
и >
>
и >
 >
перестановочны, то
>
перестановочны, то
> >
>
противоречие.
Следовательно, >
 >.
Пусть теперь >
>.
Пусть теперь >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >.
Поскольку >
>.
Поскольку >
 >
- >
>
- >
 >-максимальлная
подгруппа группы >
>-максимальлная
подгруппа группы >
 >,
то
>,
то
> >
>
Полученное
противоречие показывает, что >
 >.
Значит, >
>.
Значит, >
 >
и >
>
и >
 >.
Так как >
>.
Так как >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
то >
>,
то >
 >
- минимальная нормальная подгруппа в
группе >
>
- минимальная нормальная подгруппа в
группе >
 >.
Из того, что >
>.
Из того, что >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >,
следует, что >
>,
следует, что >
 >.
Ясно, что >
>.
Ясно, что >
 >.
Следовательно, >
>.
Следовательно, >
 >,
и поэтому >
>,
и поэтому >
 >
- нормальная подгруппа в группе >
>
- нормальная подгруппа в группе >
 >.
Допустим, что >
>.
Допустим, что >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
такая что >
>,
такая что >
 >.
Рассуждая как выше видим, что
>.
Рассуждая как выше видим, что
> >
>
противоречие.
С другой стороны, если >
 >,
то как и выше получаем, что
>,
то как и выше получаем, что
> >
>
что невозможно.
Следовательно, >
 >.
>.
Предположим
теперь, что >
 >.
Допустим, что >
>.
Допустим, что >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
такая что >
>,
такая что >
 >.
Поскольку >
>.
Поскольку >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
и >
>
и >
 >,
то >
>,
то >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
По условию >
>.
По условию >
 >
- подгруппа группы >
>
- подгруппа группы >
 >.
Следовательно, >
>.
Следовательно, >
 >,
противоречие. Используя приведенные
выше рассуждения можно показать, что
при >
>,
противоречие. Используя приведенные
выше рассуждения можно показать, что
при >
 >
этот случай также невозможен.
>
этот случай также невозможен.
Полученное
противоречие показывает, что >
 >.
Пусть >
>.
Пусть >
 >.
Тогда >
>.
Тогда >
 >,
и поэтому >
>,
и поэтому >
 >
- нормальная силовская >
>
- нормальная силовская >
 >-подгруппа
в группе >
>-подгруппа
в группе >
 >.
Значит, >
>.
Значит, >
 >,
где >
>,
где >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >
такая, что >
>
такая, что >
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >.
Пусть >
>.
Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Поскольку >
>.
Поскольку >
 >,
то >
>,
то >
 >
и поэтому >
>
и поэтому >
 >.
Значит, >
>.
Значит, >
 >
- единственная максимальная подгруппа
группы >
>
- единственная максимальная подгруппа
группы >
 >.
Следовательно, >
>.
Следовательно, >
 >
- циклическая группа. Пусть >
>
- циклическая группа. Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >,
отличная от >
>,
отличная от >
 >.
Так как
>.
Так как
> >,
>,
то >
 >.
С другой стороны, >
>.
С другой стороны, >
 >
и поэтому >
>
и поэтому >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
отличная от >
>,
отличная от >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Поскольку подгруппы >
>.
Поскольку подгруппы >
 >
и >
>
и >
 >
перестановочны и >
>
перестановочны и >
 >,
то >
>,
то >
 >
и поэтому >
>
и поэтому >
 >.
Следовательно, >
>.
Следовательно, >
 >
- единственная >
>
- единственная >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Значит, согласно теореме Error: Reference source not found,
>
>.
Значит, согласно теореме Error: Reference source not found,
>
 >
- либо циклическая группа, либо группа
кватернионов порядка >
>
- либо циклическая группа, либо группа
кватернионов порядка >
 >.
Пусть имеет место первый случай. Тогда
>
>.
Пусть имеет место первый случай. Тогда
>
 >.
Это означает, что >
>.
Это означает, что >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >,
и поэтому >
>,
и поэтому >
 >
Полученное противоречие показывает,
что первый случай невозможен. Следовательно,
>
>
Полученное противоречие показывает,
что первый случай невозможен. Следовательно,
>
 >,
где >
>,
где >
 >
- группа кватернионов порядка >
>
- группа кватернионов порядка >
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >.
>.
Пусть теперь
>
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Тогда >
>.
Тогда >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >,
и, следовательно, >
>,
и, следовательно, >
 >
- подгруппа группы >
>
- подгруппа группы >
 >.
Но поскольку >
>.
Но поскольку >
 >,
то этот случай невозможен.
>,
то этот случай невозможен.
2. Для любой
максимальной и не нормальной в >
 >
подгруппы >
>
подгруппы >
 >
имеет место >
>
имеет место >
 >,
где >
>,
где >
 >
и >
>
и >
 >
- различые простые числа. Более того, мы
теперь уже можем предполагать, что
индекс любой максимальной в >
>
- различые простые числа. Более того, мы
теперь уже можем предполагать, что
индекс любой максимальной в >
 >
подгруппы есть простое число. Это
означает, что группа >
>
подгруппы есть простое число. Это
означает, что группа >
 >
сверхразрешима, что в свою очередь
влечет сверхразрешимость подгруппы >
>
сверхразрешима, что в свою очередь
влечет сверхразрешимость подгруппы >
 >.
Пусть >
>.
Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >,
отличная от >
>,
отличная от >
 >.
Рассуждая как выше видим, что >
>.
Рассуждая как выше видим, что >
 >
- примарная циклическая подгруппа и
поэтому >
>
- примарная циклическая подгруппа и
поэтому >
 >
для некоторых >
>
для некоторых >
 >
и >
>
и >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Пусть >
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >,
пусть >
>,
пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >,
которая содержится в >
>,
которая содержится в >
 >
и пусть >
>
и пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >,
которая содержится в >
>,
которая содержится в >
 >.
Если >
>.
Если >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >,
то >
>,
то >
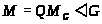 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >
не является нормальной подгруппой
группы >
>
не является нормальной подгруппой
группы >
 >.
>.
Допустим,
что >
 >.
Тогда >
>.
Тогда >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >
и >
>
и >
 >.
Из сверхразрешимости группы >
>.
Из сверхразрешимости группы >
 >
следует, что >
>
следует, что >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >.
Значит, >
>.
Значит, >
 >,
где >
>,
где >
 >
- группа простого порядка >
>
- группа простого порядка >
 >.
Ясно, что >
>.
Ясно, что >
 >
и поэтому >
>
и поэтому >
 >.
Поскольку все максимальные подгруппы
группы >
>.
Поскольку все максимальные подгруппы
группы >
 >,
отличные от >
>,
отличные от >
 >,
цикличны, то >
>,
цикличны, то >
 >
- группа типа (3).
>
- группа типа (3).
Пусть >
 >.
Тогда >
>.
Тогда >
 >
и >
>
и >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >.
Значит, >
>.
Значит, >
 >.
Так как >
>.
Так как >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
то >
>,
то >
 >
- циклическая подгруппа и >
>
- циклическая подгруппа и >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >
- группа типа (1).
>
- группа типа (1).
Пусть теперь,
>
 >
- различные простые числа. Тогда >
>
- различные простые числа. Тогда >
 >
и >
>
и >
 >.
Если >
>.
Если >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >,
то >
>,
то >
 >
и поэтому >
>
и поэтому >
 >
- группа типа (1). Пусть >
>
- группа типа (1). Пусть >
 >
не является нормальной подгруппой
группы >
>
не является нормальной подгруппой
группы >
 >.
Тогда >
>.
Тогда >
 >
- наибольший простой делитель порядка
группы >
>
- наибольший простой делитель порядка
группы >
 >
и поэтому >
>
и поэтому >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
такая что >
>,
такая что >
 >
и >
>
и >
 >.
Допустим, что >
>.
Допустим, что >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >.
Значит, в ней существует нормальная
силовская подгруппа. Если >
>.
Значит, в ней существует нормальная
силовская подгруппа. Если >
 >,
то >
>,
то >
 >
и поэтому >
>
и поэтому >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >.
Полученное противоречие показывает,
что для некоторого >
>.
Полученное противоречие показывает,
что для некоторого >
 >,
>
>,
>
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >.
Следовательно, >
>.
Следовательно, >
 >
- нормальная подгруппа группы >
>
- нормальная подгруппа группы >
 >,
противоречие. Значит, >
>,
противоречие. Значит, >
 >
не является нормальной подгруппой в
группе >
>
не является нормальной подгруппой в
группе >
 >.
Рассуждая как выше видим, что у >
>.
Рассуждая как выше видим, что у >
 >
все максимальные подгруппы отличные
от >
>
все максимальные подгруппы отличные
от >
 >
примарны и цикличны и >
>
примарны и цикличны и >
 >.
Значит, >
>.
Значит, >
 >
- группа типа (1).
>
- группа типа (1).
Достаточность.
Если >
 >
и >
>
и >
 >,
то очевидно, что любая >
>,
то очевидно, что любая >
 >-максимальная
погруппа группы >
>-максимальная
погруппа группы >
 >
перестановочна с ее максимальными
подгруппами.
>
перестановочна с ее максимальными
подгруппами.
Пусть >
 >
- группа Шмидта, где >
>
- группа Шмидта, где >
 >
- группа кватернионов порядка >
>
- группа кватернионов порядка >
 >
и >
>
и >
 >
- группа порядка >
>
- группа порядка >
 >.
Ясно, что в группе >
>.
Ясно, что в группе >
 >
>
>
>
 >-максимальные
подгруппы перестановочны со всеми
максимальными подгруппами.
>-максимальные
подгруппы перестановочны со всеми
максимальными подгруппами.
Предположим
теперь, что >
 >
- группа типа (1)-(3). Пусть >
>
- группа типа (1)-(3). Пусть >
 >
- произвольная максимальная подгруппа
группы >
>
- произвольная максимальная подгруппа
группы >
 >
и >
>
и >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Докажем, что подгруппы >
>.
Докажем, что подгруппы >
 >
и >
>
и >
 >
перестановочны.
>
перестановочны.
Пусть >
 >
- группа типа (1). Пусть >
>
- группа типа (1). Пусть >
 >.
>.
1. Пусть >
 >,
где >
>,
где >
 >
- простое число, отличное от >
>
- простое число, отличное от >
 >.
Пусть >
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >,
которая содержится в >
>,
которая содержится в >
 >.
Тогда >
>.
Тогда >
 >.
>.
Допустим,
что >
 >.
Поскольку группа >
>.
Поскольку группа >
 >
сверхразрешима, то индекс >
>
сверхразрешима, то индекс >
 >
максимальной подгруппы >
>
максимальной подгруппы >
 >
является простым числом.
>
является простым числом.
Пусть >
 >.
Тогда >
>.
Тогда >
 >.
Значит, >
>.
Значит, >
 >.
Поскольку
>.
Поскольку
> >,
>,
то >
 >
- максимальная в >
>
- максимальная в >
 >
подгруппа. Если >
>
подгруппа. Если >
 >,
то >
>,
то >
 >
- примарная циклическая группа. Так как
>
>
- примарная циклическая группа. Так как
>
 >
делит >
>
делит >
 >,
то >
>,
то >
 >,
>
>,
>
 >
и поэтому для некоторого >
>
и поэтому для некоторого >
 >,
>
>,
>
 >.
Полученное противоречие показывает,
что >
>.
Полученное противоречие показывает,
что >
 >.
Это означает, что >
>.
Это означает, что >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
>.
Допустим,
что >
 >.
Пусть >
>.
Пусть >
 >.
Тогда >
>.
Тогда >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Поскольку в >
>.
Поскольку в >
 >
любая максимальная подгруппа индекса
>
>
любая максимальная подгруппа индекса
>
 >
совпадает с >
>
совпадает с >
 >,
то >
>,
то >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >
и поэтому >
>
и поэтому >
 >
перестановочна с >
>
перестановочна с >
 >.
>.
Пусть теперь
>
 >.
Пусть >
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
и >
>-подгруппа
и >
 >
- силовская >
>
- силовская >
 >-подгруппа
в >
>-подгруппа
в >
 >
соответственно. Пусть >
>
соответственно. Пусть >
 >.
Тогда >
>.
Тогда >
 >
и поэтому для некоторого >
>
и поэтому для некоторого >
 >,
>
>,
>
 >.
Из того, что >
>.
Из того, что >
 >,
следует, что >
>,
следует, что >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
С другой стороны, >
>.
С другой стороны, >
 >
- максимальная подгруппа циклической
группы >
>
- максимальная подгруппа циклической
группы >
 >.
Значит, >
>.
Значит, >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >
и поэтому >
>
и поэтому >
 >
- нормальная подруппа в >
>
- нормальная подруппа в >
 >.
Следовательно, >
>.
Следовательно, >
 >
перестановочна с >
>
перестановочна с >
 >.
Пусть >
>.
Пусть >
 >.
Тогда для некоторого >
>.
Тогда для некоторого >
 >,
>
>,
>
 >.
Рассуждая как выше видим, что >
>.
Рассуждая как выше видим, что >
 >.
Значит, >
>.
Значит, >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Поскольку
>.
Поскольку
> >,
>,
то >
 >.
Это означает, что подгруппы >
>.
Это означает, что подгруппы >
 >
и >
>
и >
 >
перестановочны. Пусть >
>
перестановочны. Пусть >
 >.
Используя приведенные выше рассуждения
видим, что >
>.
Используя приведенные выше рассуждения
видим, что >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Поскольку >
>.
Поскольку >
 >,
то >
>,
то >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Следовательно, подгруппы >
>.
Следовательно, подгруппы >
 >
и >
>
и >
 >
перестановочны. Пусть >
>
перестановочны. Пусть >
 >.
Рассуждая как выше видим, что >
>.
Рассуждая как выше видим, что >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >
и >
>
и >
 >.
Значит, >
>.
Значит, >
 >.
Следовательно, подгруппы >
>.
Следовательно, подгруппы >
 >
и >
>
и >
 >
перестановочны. Пусть теперь >
>
перестановочны. Пусть теперь >
 >.
Поскольку >
>.
Поскольку >
 >,
то >
>,
то >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Пусть >
>.
Пусть >
 >.
Тогда >
>.
Тогда >
 >,
где >
>,
где >
 >.
Пусть >
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
группы >
>-подгруппа
группы >
 >.
Пусть >
>.
Пусть >
 >.
Тогда >
>.
Тогда >
 >
- >
>
- >
 >-группа
и для некоторого >
>-группа
и для некоторого >
 >,
>
>,
>
 >.
Без ограничения общности можно
предположить, что >
>.
Без ограничения общности можно
предположить, что >
 >.
Поскольку >
>.
Поскольку >
 >,
то >
>,
то >
 >.
Значит, >
>.
Значит, >
 >.
Следовательно, подгруппы >
>.
Следовательно, подгруппы >
 >
и >
>
и >
 >
перестановочны. Пусть >
>
перестановочны. Пусть >
 >.
Тогда >
>.
Тогда >
 >.
Следовательно, >
>.
Следовательно, >
 >
и поэтому подгруппа >
>
и поэтому подгруппа >
 >
перестановочна с >
>
перестановочна с >
 >.
Пусть >
>.
Пусть >
 >.
Тогда >
>.
Тогда >
 >.
Ясно, что >
>.
Ясно, что >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Это означает, что подгруппы >
>.
Это означает, что подгруппы >
 >
и >
>
и >
 >
перестановочны. Пусть >
>
перестановочны. Пусть >
 >.
Тогда >
>.
Тогда >
 >.
Поскольку >
>.
Поскольку >
 >,
то
>,
то
> >
>
и поэтому
подгруппы >
 >
и >
>
и >
 >
перестановочны.
>
перестановочны.
Если >
 >,
то рассуждая подобным образом, получаем,
что >
>,
то рассуждая подобным образом, получаем,
что >
 >
перестановочна с >
>
перестановочна с >
 >.
>.
Допустим,
что >
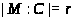 >.
Так как в >
>.
Так как в >
 >
все максимальные подгруппы, отличные
от >
>
все максимальные подгруппы, отличные
от >
 >,
примарные и циклические, то >
>,
примарные и циклические, то >
 >
- максимальная подгруппа в >
>
- максимальная подгруппа в >
 >.
Следовательно, >
>.
Следовательно, >
 >.
Это означает, что в группе >
>.
Это означает, что в группе >
 >
существует единственная >
>
существует единственная >
 >-максимальная
подгруппа >
>-максимальная
подгруппа >
 >
и она единична. Таким образом, >
>
и она единична. Таким образом, >
 >
перестановочна с >
>
перестановочна с >
 >.
>.
2. Пусть теперь
>
 >.
>.
Пусть >
 >.
Тогда >
>.
Тогда >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >
и поэтому >
>
и поэтому >
 >
перестановочна с >
>
перестановочна с >
 >.
Пусть >
>.
Пусть >
 >.
Тогда >
>.
Тогда >
 >.
Поскольку для некоторого >
>.
Поскольку для некоторого >
 >,
>
>,
>
 >,
то без ограничения общности можно
предположить, что >
>,
то без ограничения общности можно
предположить, что >
 >.
Значит, >
>.
Значит, >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >
и поэтому
>
и поэтому
> >
>
Допустим,
что >
 >.
Тогда >
>.
Тогда >
 >
- >
>
- >
 >-группа.
Поскольку для некоторого >
>-группа.
Поскольку для некоторого >
 >,
>
>,
>
 >
и >
>
и >
 >,
то >
>,
то >
 >
и поэтому >
>
и поэтому >
 >.
Пусть теперь >
>.
Пусть теперь >
 >.
Пусть >
>.
Пусть >
 >
- силовская >
>
- силовская >
 >-подгруппа
и >
>-подгруппа
и >
 >
- силовская >
>
- силовская >
 >-подгруппа
в >
>-подгруппа
в >
 >
соответственно. Тогда >
>
соответственно. Тогда >
 >.
Ясно, что >
>.
Ясно, что >
 >
для некоторого >
>
для некоторого >
 >
и >
>
и >
 >.
Следовательно, >
>.
Следовательно, >
 >
и поэтому >
>
и поэтому >
 >.
Если >
>.
Если >
 >,
то
>,
то
> >
>
Если >
 >,
то
>,
то
> >
>
В любом
случае, >
 >-максимальная
подгруппа >
>-максимальная
подгруппа >
 >
перестановочна с максимальной подгруппой
>
>
перестановочна с максимальной подгруппой
>
 >.
>.
Пусть >
 >
- группа типа (2) или (3). Если >
>
- группа типа (2) или (3). Если >
 >,
то >
>,
то >
 >.
Поскольку >
>.
Поскольку >
 >,
то >
>,
то >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >
содержится в некоторой максимальной
циклической подгруппе >
>
содержится в некоторой максимальной
циклической подгруппе >
 >
группы >
>
группы >
 >.
Так как >
>.
Так как >
 >,
то >
>,
то >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Отсюда следует, что
>.
Отсюда следует, что
> >
>
Значит, >
 >
перестановочна с >
>
перестановочна с >
 >.
Пусть >
>.
Пусть >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >
для некоторого >
>
для некоторого >
 >.
Поскольку >
>.
Поскольку >
 >
то
>
то
> >
>
и поэтому >
 >
перестановочна с >
>
перестановочна с >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >.
Из того, что >
>.
Из того, что >
 >,
следует, что >
>,
следует, что >
 >.
Значит, >
>.
Значит, >
 >
перестановочна с >
>
перестановочна с >
 >.
>.
Пусть теперь
>
 >.
Тогда >
>.
Тогда >
 >
- >
>
- >
 >-группа
и, следовательно, для некоторого >
>-группа
и, следовательно, для некоторого >
 >,
>
>,
>
 >
. Без ограничения общности можно
предположить, что >
>
. Без ограничения общности можно
предположить, что >
 >.
Ясно, что >
>.
Ясно, что >
 >
- >
>
- >
 >-максимальная
подгруппа группы >
>-максимальная
подгруппа группы >
 >.
Пусть >
>.
Пусть >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >,
содержащая >
>,
содержащая >
 >.
Допустим, что >
>.
Допустим, что >
 >.
Если >
>.
Если >
 >,
то >
>,
то >
 >.
Предположим, что >
>.
Предположим, что >
 >.
Тогда >
>.
Тогда >
 >
- циклическая группа. Поскольку >
>
- циклическая группа. Поскольку >
 >,
то >
>,
то >
 >
- максимальная подгруппа группы >
>
- максимальная подгруппа группы >
 >.
Из того, что >
>.
Из того, что >
 >
- циклическая подгруппа следует, что >
>
- циклическая подгруппа следует, что >
 >.
Значит, >
>.
Значит, >
 >.
Поскольку >
>.
Поскольку >
 >,
то >
>,
то >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Отсюда следует, что >
>.
Отсюда следует, что >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Значит, >
>.
Значит, >
 >
перестановочна с >
>
перестановочна с >
 >.
>.
Пусть >
 >.
Поскольку >
>.
Поскольку >
 >
- циклическая группа, то >
>
- циклическая группа, то >
 >
- нормальная подгруппа в >
>
- нормальная подгруппа в >
 >.
Следовательно, >
>.
Следовательно, >
 >
перестановочна с >
>
перестановочна с >
 >.
Теорема доказана.
>.
Теорема доказана.
Если в
группе >
 >
любая ее максимальная подгруппа
перестановочна со всеми >
>
любая ее максимальная подгруппа
перестановочна со всеми >
 >-максимальными
подгруппами группы >
>-максимальными
подгруппами группы >
 >
и >
>
и >
 >,
то >
>,
то >
 >
- нильпотентная группа.
>
- нильпотентная группа.
Легко видеть, что классы групп теоремы попарно не пересекаются. Отметим, что, как и в случае теоремы, можно построить примеры групп типов (1) - (3).
Заключение
В данной
работе дано описание групп, у которых
максимальные подгруппы перестановочны
с >
 >-максимальными
подгруппами групп; описание ненильпотентных
групп, у которых каждая >
>-максимальными
подгруппами групп; описание ненильпотентных
групп, у которых каждая >
 >-максимальная
подгруппа перестановочна со всеми
>
>-максимальная
подгруппа перестановочна со всеми
>
 >-максимальными
подгруппами; описание ненильпотентных
групп, у которых каждая максимальная
подгруппа перестановочна со всеми
>
>-максимальными
подгруппами; описание ненильпотентных
групп, у которых каждая максимальная
подгруппа перестановочна со всеми
>
 >-максимальными
подгруппами. Доказана >
>-максимальными
подгруппами. Доказана >
 >-разрешимость
и найдены оценки >
>-разрешимость
и найдены оценки >
 >-длины
групп, у которых каждая >
>-длины
групп, у которых каждая >
 >-максимальная
подгруппа >
>-максимальная
подгруппа >
 >-перестановочна
со всеми >
>-перестановочна
со всеми >
 >-максимальными
подгруппами, где >
>-максимальными
подгруппами, где >
 >.
>.
Литература
1.Боровиков М.Т. Группы с перестановочными подгруппами взаимно простых порядков // Вопросы алгебры. Выпуск 5. - Минск: Университетское, 1990. - С. 80-82.
2.Боровиков
М.Т. О >
 >-разрешимости
конечной группы // Арифметическое и
подгрупповое строение конечных групп
/ Под редакцией М.И. Салука. - Минск: Наука
и техника, 1986. - С. 3-7.
>-разрешимости
конечной группы // Арифметическое и
подгрупповое строение конечных групп
/ Под редакцией М.И. Салука. - Минск: Наука
и техника, 1986. - С. 3-7.
3.Белоногов
В.А. Конечные разрешимые группы с
нильпотентными >
 >-максимальными
подгруппами // Матем. заметки. - 1968. - Т.
3, № 1. - С. 21-32.
>-максимальными
подгруппами // Матем. заметки. - 1968. - Т.
3, № 1. - С. 21-32.
4.Беркович Я.Г. Конечные группы с дисперсивными вторыми максимальными подгруппами // Докл. АН СССР. - 1964. - Т. 158, № 5. - С. 1007-1009.
5.Беркович
Я.Г. Конечные группы, у которых все >
 >-е
максимальные подгруппы являются
обобщенными группами Шмидта // Мат.
заметки. - 1969. - Т. 5, № 1. - С. 129-136.
>-е
максимальные подгруппы являются
обобщенными группами Шмидта // Мат.
заметки. - 1969. - Т. 5, № 1. - С. 129-136.
6.Беркович Я.Г. Конечные неразрешимые группы с абелевыми третьими максимальными подгруппами // Изв. высш. учебн. заведений. Математика. - 1969. - № 7. - С. 10-15.
7.Беркович Я.Г., Пальчик Э.М. О перестановочности подгрупп конечной группы // Сиб. мат. журн. - 1967. - Т. 8, № 4. - С. 741-753.
8.Веньбинь
Го, Шам К.П., Скиба А.Н., >
 >-накрывающие
системы подгрупп для классов
>
>-накрывающие
системы подгрупп для классов
>
 >-сверхразрешимых
и >
>-сверхразрешимых
и >
 >-нильпотентных
конечных групп // Сиб. мат. журнал. - 2004.
- Т. 45, № 3. - С. 75-92.
>-нильпотентных
конечных групп // Сиб. мат. журнал. - 2004.
- Т. 45, № 3. - С. 75-92.
9.Голубева О.В., Пальчик Э.М. К теореме Виланда // Весцi НАН Беларусi. Сер. фiз.-матэм. навук. - 2001. - № 3. - С. 135-136.
10.Курносенко Н.М. О факторизации конечных групп сверхразрешимыми и нильпотентными подгруппами // Вопросы алгебры. Выпуск 12. - 1998. С. 113-122.
11.Пальчик
Э.М. О >
 >-квазинормальных
подгруппах // Докл. АН БССР. - 1967. - Т. 11, №
11. - С. 967-969.
>-квазинормальных
подгруппах // Докл. АН БССР. - 1967. - Т. 11, №
11. - С. 967-969.
12.Пальчик
Э.М. О группах, все >
 >-максимальные
подгруппы которых перестановочны с
силовской подгруппой // ИАН БССР. Сер.
физ.-матем. наук. - 1968. - № 1. - С. 45-48.
>-максимальные
подгруппы которых перестановочны с
силовской подгруппой // ИАН БССР. Сер.
физ.-матем. наук. - 1968. - № 1. - С. 45-48.
13.Пальчик Э.М. О конечных группах с перестановочными подгруппами // Докл. АН БССР. - 1967. - Т. 11, № 5. - С. 391-392.