Использование расчетных формул в задачах
Задача 1.
Определить центр тяжести сечения.

Решение
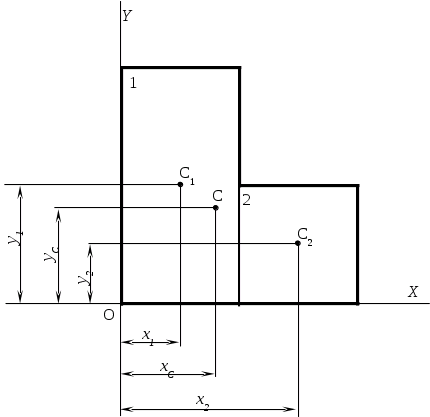
Укажем оси координат X и Y с началом в нижнем левом углу сечения.
Сечение разобьем на два простых сечения – прямоугольник 1 с центром тяжести С>1> и квадрат 2 с центром тяжести С>2>.
Координаты центра тяжести С сечения находим по формулам:
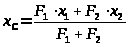 и
и
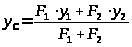 ,
где
,
где
x>1> = 15 мм - координата центра тяжести С>1> прямоугольника по оси Х;
y>1> = 30 мм - координата центра тяжести С>1> прямоугольника по оси Y;
x>2> = 45 мм - координата центра тяжести С>2> квадрата по оси Х;
y>2> = 15 мм - координата центра тяжести С>2> квадрата по оси Y;
F>1>
=
 =
1800 мм2 - площадь прямоугольника;
=
1800 мм2 - площадь прямоугольника;
F>2>
=
 =
900 мм2 - площадь квадрата.
=
900 мм2 - площадь квадрата.
Тогда
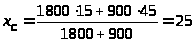 мм,
мм,
 мм.
мм.
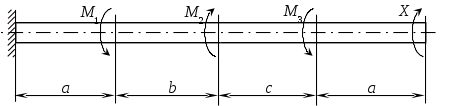
Задача 2.
К стальному валу приложены три известных момента М>1>, М>2>, М>3>. Требуется: 1) установить, при каком значении момента Х угол поворота правого концевого сечения вала равно нулю; 2) для найденного значения Х построить эпюру крутящих моментов; 3) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его значение до ближайшего, равного 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм; 4) построить эпюру углов закручивания; 5) найти наибольший относительный угол закручивания (на 1 м).
Для стали принять G
=
 МПа.
Полярный момент инерции
МПа.
Полярный момент инерции
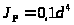 м4
м4
a = 1,9 м, b = 1,2 м, c = 1,4 м,
М>1> = 1900 Нм, М>2> = 1200 Нм,
М>3> = 1700 Нм, [τ] = 75 МПа.
Решение.
1) Угол поворота правого концевого сечения определяется как алгебраическая сумма взаимных углов поворота сечений на участках АВ, BC, CD, DE
 .
.
Отсюда определим момент X


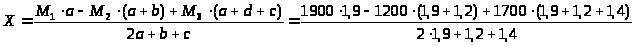 Х
= 1178,125 Нм
Х
= 1178,125 Нм
2) Строим эпюру крутящих моментов M>К >(см. рис а)
Определяем опорные реакции. Отбросив опору (в данном случае защемление), заменим ее возможными реакциями. Т. к. все активные силы представляют собой крутящие моменты, то в опоре возникает только одно воздействие крутящий момент М>Е>, который определим из уравнения равновесия:
 ;
М>Е>
– 1900 + 1200 – 1700 + 1178,125 = 0
;
М>Е>
– 1900 + 1200 – 1700 + 1178,125 = 0
М>Е> = 1900 – 1200 + 1700 – 1178,125 = 1221,875 Нм
При построении эпюры крутящих моментов М>К> применяем метод сечений дл каждого из четырех участков.
Для участка DE:
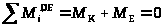 ;
;
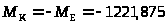 Нм
Нм

Для участка CD:
 ;
;
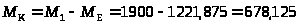 Нм
Нм
Для участка ВС:
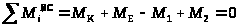 ;
;
 Нм
Нм
Для участка АВ:
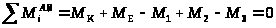 ;
;
 Нм
Нм
3) Определяем диаметр вала
Из эпюры максимальный М>К>
= 1221,875 Нм на участке DE.
На этом участке возникает максимальное
касательное напряжение
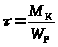 ,
где W>P>
– момент сопротивления сечения
,
где W>P>
– момент сопротивления сечения

Приравнивая τ [τ], определим диаметр вала

 0,043
м или 43 мм,
0,043
м или 43 мм,
Согласно условиям задачи принимаем d = 45 мм.
4) Строим эпюру углов закручивания (см. рис. в) для всех участков по формуле
 .
.
Выбираем начало координат в точке Е.
Участок DE:
Угол поворота сечения, взятого на расстоянии z от неподвижного сечения Е, будет
 ,
где
,
где
 ;
;
при z = 0 φ = 0;
при z = a = 1,9 м
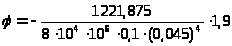 =
– 0,071 рад.
=
– 0,071 рад.
Участок CD:
 ,
где
,
где

при z = а = 1,9 м φ = – 0,071 рад;
при z
= (a
+ b)
= 3,1 м
 =
– 0,046 рад.
=
– 0,046 рад.
Участок BC:
 ,
где
,
где

при z = (а + b) = 3,1 м φ = – 0,046 рад;
при z
= (a
+ b
+c)
= 4,5 м
 =
– 0,068 рад.
=
– 0,068 рад.
Участок AB:
 ,
где
,
где

при z = (а + b + c) = 4,5 м φ = – 0,068 рад;
при z
= (2a
+ b
+ c)
= 6,4 м
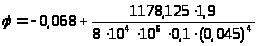 =
0 рад.
=
0 рад.
5) Наибольший относительный угол закручивания будет на участке DE
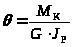 =
= =
0,037 рад/м
=
0,037 рад/м
Задача 3.
Для поперечного сечения, составленного из стандартных прокатных профилей, требуется:
определить положение центра тяжести;
найти значения осевых и центробежных моментов инерции относительно горизонтальной и вертикальной осей, проходящих через центр тяжести сечения;
определить направления главных центральных осей инерции;
найти значения моментов инерции относительно главных центральных осей;
вычертить сечение в масштабе 1:2 и указать на нем все оси и размеры.
Схема сечения состоит из двух прокатных профилей:
профиля I - швеллера № 30,
профиля II - двутавра № 33.
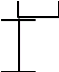
Решение.
Геометрические характеристики швеллера берем по ГОСТ 8240-72:
hI = 300 мм, bI = 100 мм, dI = 6,5 мм, tI = 11 мм,
 см4,
см4,
 см4,
А>1>
= 40,5 см2, z>0>
= 2,52 см.
см4,
А>1>
= 40,5 см2, z>0>
= 2,52 см.
Геометрические характеристики двутавра берем по ГОСТ 8239-72:
hII = 330 мм, bII = 140 мм, dII = 7 мм, tII = 11,2 мм,
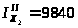 см4,
см4,
 см4,
А>2>
= 53,8 см2.
см4,
А>2>
= 53,8 см2.
Выбираем вспомогательные оси V, Z и определяем относительно их координаты центра тяжести составного сечения
 19,7
см;
19,7
см;
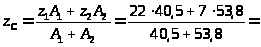 13,4
см.
13,4
см.
Вспомогательные центральные оси X>C> и Y>C> параллельны осям V и Z.
Вычисляем осевые и центробежные моменты инерции относительно этих осей. Центральные вспомогательные оси X>C> и Y>C> параллельны осям центральным осям швеллера и двутавра, относительно которых моменты инерции известны.
Тогда
Осевые моменты инерции
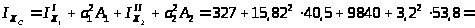
 см4
=
см4
=
 м4
м4

 см4
=
см4
=
 м4
м4
Центробежный момент инерции
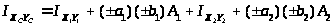
Для швеллера оси X>1>,
Y>1>
являются главными, поэтому
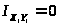 .
Для двутавра оси X>2>,
Y>2>
являются главными, поэтому
.
Для двутавра оси X>2>,
Y>2>
являются главными, поэтому
 .
.
Тогда
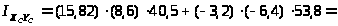
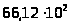 см4
=
см4
=
 м4
м4

Определяем положение главных осей инерции составного сечения (угол наклона) к исходной оси X>C>
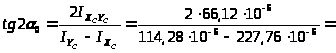 –1,165
–1,165
 .
.
Определяем главные моменты инерции составного сечения по формулам

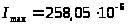 м4;
м4;
 м4.
м4.
Проверим правильность расчетов по выполнению соотношений

 м4
м4
 м4
м4
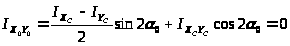
 ,
то есть расчет произведен точно.
,
то есть расчет произведен точно.
Задача 4.
Определить диаметр стального вала постоянного сечения из условия прочности, приняв [τ] = 30 Н/мм2. Мощности P>1> = 52 кВт, Р>2> = 100 кВт, Р>3> = 60 кВт. Угловая скорость ω = 32 рад/с.
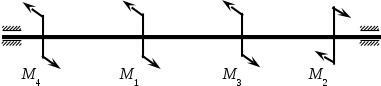
Решение
Разбиваем вал на три участка – по сечениям, в которых приложены вращающие моменты. Находим вращающие моменты
 =
1625 Нм,
=
1625 Нм,
 =
3125 Нм,
=
3125 Нм,
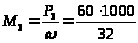 =
1875 Нм.
=
1875 Нм.
Равномерное вращение обеспечивается условием
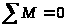 ;
;
 =0;
=0;
 =
– 375 Нм.
=
– 375 Нм.
Знак «–» указывает, что момент M>4> направлен в противоположную сторону, указанному в условии задачи.
Крутящий момент на участке 1

Справа
 ;
;
 3125
Нм.
3125
Нм.
Крутящий момент на участке 2
Справа
 ;
;
 3125
– 1875 = 1250 Нм.
3125
– 1875 = 1250 Нм.
Крутящий момент на участке 3
Справа
 ;
;
 1625
+ 3125 – 1875 = 375 Нм.
1625
+ 3125 – 1875 = 375 Нм.
По полученным результатам строим эпюру.
Диаметр вала определяем для наиболее напряженного участка.
Наиболее напряженный участок –
первый –
 3125
Нм.
3125
Нм.
Касательное напряжение сечения
вала
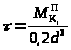 .
Из условия прочности
.
Из условия прочности
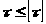 .
.
Отсюда
 =
80,5 мм.
=
80,5 мм.