Изучение матриц

1. Дайте определение алгебраического дополнения элемента определителя. Приведите пример вычисления алгебраического дополнения элемента а>12> определителя 3-го порядка

Алгебраическим дополнением А>ij> элемента а>ij> определителя n го порядка называется минор этого элемента, взятый со знаком (-1)i+j, где i+j – сумма номеров строки и столбца, которым принадлежит элемент а>ij>. Т.е. по определению А>ij>=(-1)i+j М>ij>.

Для определителя найти алгебраические дополнения элементов а>12>.

Для элемента а12 i=1, j=2 и i+j=3 число нечетное, отсюда

2. Разложите по теореме Лапласа определитель третьего порядка, записанный в общем виде по элементам второй строки

Вычисляем определитель путем разложения его по 2-ей строке

3. Какая система линейных алгебраических уравнений называется неоднородной? Какое решение имеет система неоднородных линейных уравнений, если главный определитель не равен нулю?

Система уравнений называется неоднородной, если хотя бы один свободный член уравнения не равен нулю.

Если главный определитель системы n уравнений с n неизвестными не равен нулю, то система имеет единственное решение, корни которого определяются по формулам:

, , …,

4. Дайте определение матрицы и ее размера. Приведите пример матриц размеров: 1х3, 3х4,1х1.

Матрицей называется таблица чисел или каких-либо других элементов, содержащая m строк и n столбцов.

Общий вид матрицы

Матрица имеет размер, который определяется ее количеством строк и столбцов, что записывается так – А>m>>>>n>.

Например, числовая матрица размером 11 имеет вид , размером 13 имеет вид , размером 34 имеет вид .

5. Что такое союзная или присоединенная матрица? Приведите пример вычисления союзной матрицы для заданной.

Если для заданной квадратной матрицы А определить алгебраические дополнения всех ее элементов и затем транспонировать их, то полученная таким образом матрица будет называться союзной или присоединенной по отношению к матрице А и обозначаться символом Ã

Для матрицы найти Ã.

Составляем определитель матрицы А

Определяем алгебраические дополнения всех элементов определителя по формуле

; ;

.

; ;

.

; ;

.

Транспонируя полученные алгебраические дополнения, получаем союзную или присоединенную матрицу Ã по отношению заданной матрицы А.

6. Вычислить определитель 3 го порядка, разложив его по 1 й строке

7. Определить алгебраические дополнения элементов 2 й строки определителя 3-го порядка

Для элемента а>21> i=2, j=1 и i+j=3 число нечетное, отсюда

Для элемента а>22> i=2, j=2 и i+j=4 число четное, отсюда

Для элемента а>23> i=2, j=3 и i+j=5 число нечетное, отсюда

8. Найти решение системы уравнений методом Крамера

Данная система уравнений будет иметь единственное решение только тогда, когда определитель составленный из коэффициентов при X>1 - n> не будет равен нулю. Обозначим этот определитель знаком – Δ. Если этот определитель не равен нулю, то решаем дальше. Тогда каждый X>i> = Δ>i> / Δ, где Δ>i> – это определитель составленный из коэффициентов при X>1 - n>, только значения коэффициентов в i – ом стольбце заменены на значения за знаком равенства в сисетеме уравнений, а Δ – это главный определитель

Решение

Запишем систему в виде:

Главный определить

9. Выполните операцию произведения двух матриц АхВ

Решение

Найти матрицу |C| = |A| x |B|

Вычислим элементы матрицы |C|:

c>1,1> = a>1,1>b>1,1>+a>1,2>b>2,1>

c>1,2> = a>1,1>b>1,2>+a>1,2>b>2,2>

c>2,1> = a>2,1>b>1,1>+a>2,2>b>2,1>

c>2,2> = a>2,1>b>1,2>+a>2,2>b>2,2>

c>1,1> =

2

*

1

+

1

*

4

=

2

+

4

=

6

c>1,2> =

2

*

-2

+

1

*

0

=

-4

+

0

=

-4

c>2,1> =

-3

*

1

+

4

*

4

=

-3

+

16

=

13

c>2,2> =

-3

*

-2

+

4

*

0

=

6

+

0

=

6

Результирующая матрица |С|:

6

-4

13

6

10. Какие величины называются скалярными и векторными? Приведите примеры скалярных и векторных величин? Каково условие равенства векторов? Приведите пример сложения двух векторов по правилу параллелограмма и треугольника

Скалярной величиной или просто скаляром называется величина, которая при определённом выборе единицы измерения определяется числом (удельный вес, плотность, работа, мощность, температура и т.д.)

Вектор – направленный отрезок, имеющий определённую величину (скорость, ускорение, сила, напряженность магнитного и электрического поля и т.д.).

Скалярная величина – 10 минут, векторная – 100 км/ч.

Два вектора и равны, если они равнонаправлены и имеют один и тот же модуль.

Правило треугольника

Для того чтобы сложить два вектора и нужно переместить вектор параллельно самому себе (рис. 1, б) так, чтобы его начало (точка B на рис. 1, а) совпадало с концом вектора (точка A на рис. 1, а). Тогда их суммой будет вектор (рис. 1, г), начало которого совпадает с началом вектора (точка D на рис. 1, в), а конец – с концом вектора (точка C на рис. 1, в).

а б

в г

Рис. 1.

Правило параллелограмма

Для того чтобы сложить два вектора и нужно переместить их параллельно самим себе так, чтобы начала векторов и находились в одной точке (рис. 2, а). Затем построить параллелограмм, сторонами которого будут эти вектора (рис. 2, б). Тогда их суммой будет вектор (рис. 2, в), начало которого совпадает с общим началом векторов (точка A на рис. 2, б), а конец – с противоположной вершиной параллелограмма (точка В на рис. 2, б).

а

б в

Рис. 2.

11. Напишите формулу разложения вектора по трем взаимно перпендикулярным осям координат

12. Как определяется вектор через координаты его начала и конца?

Пусть известны координаты начала вектора А(x>1>, y>1>, z>1>) и его конца В(x>2>, y>2>, z>2>). Точки А и В определяют радиус вектора

z

и .


0

Рис. 3

Из треугольника ОАВ следует, что , отсюда .

Если обозначить через X, Y, Z – координаты вектора , т.е. =(X, Y, Z), то следует, что

X=х>2>-х>1>

Y=у>2>-у>1>

Z=z>2>-z>1>

Чтобы найти абсциссу вектора Х, необходимо из абсциссы конца вектора вычесть абсциссу начала вектора.

12. Какой вид имеет уравнение прямой в плоскости, проходящей через две точки?

>>

13. Какой вид имеет уравнение прямой с угловым коэффициентом?

14. Напишите разложение вектора по трем взаимно перпендикулярным осям координат

Координаты вектора

X

-2

Y

4

Z

7

A (-2, 4, 7) означает, что абсцисса точки A x=-2, ордината у=4, аппликата z=7.

15. Чему равно скалярное произведение векторов и ? Данные для варианта взять из таблицы 2.3

Координаты вектора

X

-2

Y

4

Z

7

Координаты вектора

X

3

Y

6

Z

4

Т.к. векторы заданы в координатной форме, то по формуле имеем:

16. Найти уравнение прямой, проходящей через точку пересечения прямых l>1> и l>2> и отсекающей на оси абсцисс отрезок, равный d

Уравнение прямой l>1>

Уравнение прямой l>2>

d

Координаты точки Р

x

y

3x 2y 7=0

x+3y 6=0

3

2

5

Отсюда находим х = 6 – 3у

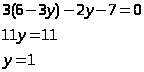
x = 3

Значит точка пересечения двух прямых A (3; 1)

По условия отрезок равен 3, значит координата точки B (3; 0).

Найдем уравнение прямой, проходящей через точки А и В.

Здесь знаменатель равен нулю. Полагаем числитель левой части равным нулю.

Получаем

17. Найти уравнение прямой, отсекающей на оси ординат отрезок, равный d и проходящей параллельно прямой l>1>

Уравнение прямой l>1>

Уравнение прямой l>2>

d

Координаты точки Р

x

y

3x 2y 7=0

x+3y 6=0

3

2

5

Найдем две точки прямой 3x 2y 7=0

Подставим в уравнение х=1 и х=3 и получим значения у соответственно -2 и 1.

A (1; – 2) и B (3; 1).

Координаты направляющего вектора найдём по координатам конца и начала вектора

Подставляя в формулу координаты точки O (0; 3) и координаты вектора получим искомое уравнение прямой

или .

18. Как определяются горизонтальные асимптоты функции

В случае если наклонная асимптота расположена горизонтально, то есть при , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота – частный случай наклонной асимптоты; прямая y = с = const является горизонтальной асимптотой графика y = f(x) при или , если

или

соответственно.

19. Что такое частное приращение функции нескольких переменных?

Частной производной функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных в точке частные производные определяются так:

,

,

если эти пределы существуют.

Из определения следует геометрический смысл частной производной функции двух переменных: частная производная – угловой коэффициент касательной к линии пересечения поверхности и плоскости в соответствующей точке.

20. Каковы выражения для частных дифференциалов функции z=f (x, y)?

Частной производной по x функции z = f (x, y) в точке M>0>(x>0>, y>0>) называется предел ,

если этот предел существует. Обозначается эта частная производная любым из следующих символов:

;;.

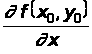Частная производная по x есть обычная производная от функции z = f (x, y), рассматриваемой как функция только от переменной x при фиксированном значении переменной y.

Совершенно аналогично можно определить частную производную по y функции z = f (x, y) в точке M>0>(x>0>, y>0>):

=.

Приведем примеры вычисления частных производных

21. Каково выражение для полного дифференциала функции u=u (x, y, z)?

Полный дифференциал du функции u = f (x, y, z) (если он существует) равен сумме всех ее частных дифференциалов:

22. Напишите частные производные третьего порядка для функции z=f (x, y, z)

23. Найти частную производную и частный дифференциал функции.

24. Вычислить значения частных производных f’>x>(M>0>), f’>y>(M>0>), f’>z>(M>0>) для данной функции f (x, y, z) в точке M>0>(x>0>, y>0>, z>0>) с точностью до двух знаков после запятой

25. Вычислить значения частных производных функции z (x, y), заданной неявно, в данной точке M>0>(x>0>, y>0>, z>0>) с точностью до двух знаков после запятой

lnZ=x+2y-z+ln3 M>0>(1,1,3)

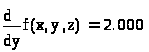
26. Найти уравнение касательной плоскости и нормали к заданной поверхности S в точке M>0>(x>0>, y>0>, z>0>). S: z=x2+y2-4xy+3x 15, M>0>(-1,3,4)

Следовательно, уравнение касательной плоскости будет таким:

а уравнение нормали таким: