Застосування координатного методу в стереометрії
1
Зміст
Вступ
Просторова декартова прямокутна система координат.
Рівняння прямої та площини у просторі.
Умова паралельності та перпендикулярності двох прямих, двох площин, прямої та площини у просторі.
Доказ координатним методом теореми про три перпендикуляри.
Вивід методом координат ознаки паралельності двох площин.
Рівняння сфери. Властивість перетину кулі площиною.
Висновки
Список використаної літератури
Вступ
При вивченні геометрії в просторі методом координат частіше всього розглядають поверхні. Метод координат полягає в тому, що завдяки координатам точок геометричні об’єкти задають аналітично за допомогою чисел,рівнянь, нерівностей та їх систем і тим самим при доведенні теорем або розв’язанні геометричних завдань використовують аналітичні методи. Це суттєво спрощує розмірковування та часто дозволяє доводити теореми або розв’язувати задачі, користуючись певним алгоритмом ( виконуючи ті чи інші обчислення), в той час, як синтетичний метод в геометрії в більшості випадків вимагає штучних прийомів. Але для того, щоб користуватися методом координат, необхідно вміти за допомогою чисел, рівнянь, нерівностей та їх систем завдавати геометричні фігури.
Просторова декартова прямокутна система координат.
Візьмемо три взаємно перпендикулярні прямі x, y, z, що перетинаються в одній точці О (див. мал. 1). Проведемо через кожну пару цих прямих площину. Площина, що проходить через прямі х та у, зветься площиною ху. Дві інші площини звуться відповідно xz та yz. Прямі x, y, z звуться кординатними осями або осями координат, точка їх перетину О- початком координат, а площини xy, yz, та xz- координатними площинами. Точка О розбиває кожну з осей координат на дві напівпрямі. Умовимся одну з них називати додатньою, а іншу- від’ємною.
Візьмемо тепер довільну точку А та проведем через неї площину, паралельну площині yz. Вона перетинає вісь х в деякій точці А>х>. Координатою х точки А будемо називати число, рівне за абсолютною велчиною довжині відрізка ОА>х>, додатнє, якщо точка А>х> розташована на додатній півосі х, та від’ємне, якщо вона розташована на від’ємній півосі. Якщо точка А>х> співпадає з точкою О, то приймаємо х=0. Аналогічно визначаються координати y, z точки А. Координати точки будемо записувати в дужках поряд з літерним позначенням точки: А (x, y, z). Іноді будемо позначати точку просто її координатами (x, y, z).
Відстань між двома точками А>1> (x>1>,y>1>,z>1>) та А>2> (x>2>,y>2>,z>2>) визначається співвідношенням:
Нехай
А (x>1>,y>1>,z>1>)
та В (x>2>,y>2>,z>2>)
дві довільні точки. Координати x,
y,
z
точки С, що ділить
відрізок АВ у відношенні
через координати точок А та В визначаються
слідуючим чином:
z
xz
xz
yz J
O
x
xy
y
Малюнок 1- Просторова декартова прямокутна система координат
Рівняння прямої та площини у просторі.
Нехай d- пряма у просторі. Будь-який ненульовий вектор, що паралельний цій прямій, зветься її напрямним вектором. Ясно, що пряма має нескінчену множину направляючих векторів, будь-які два з яких колінеарні. Всі ці вектори,разом з нульовим вектором, утворюють одномірний векторний підпростір, що зветься направляючим підпростіром прямої d.
Положення прямої d у просторі визначається повністю, якщо задані:
направляючий вектор прямої d та деяка точка;
дві точки прямої;
дві площини, що перетинаються по прямій d.
Поставимо задачу: для кожного з цих способів задання прямої написати її рівняння.
Канонічне
рівняння прямої.
Нехай у просторі обрана прямокутна
декартова система координат і в цій
системі відомі координати деякої точки
М>0>
(x>0>,
y>0>,z>0>)
та координати
направляючого вектора
прямої d.
Напишемо рівняння цієї прямої. Спочатку
розглянемо той випадок, коли жодна з
координат вектора не дорівнює нулю.
Очевидно, точка
М (x,
y,
z)
розташована на
прямій d
тоді і тільки тоді, коли вектори
та
колінеарні. Вектор
має координати (х-х>0>,
y-y>0>,
z-z>0>).
Враховуючи умову колінеарності, можна
записати рівняння прямої d:
(1)
Якщо
одна з координат вектора
дорівнює нулю, наприклад:
, то умова колінеарності запишеться
так:
(2)
Аналогічно,
якщо дорівнюють нулю дві координати
вектора
,
наприклад:
,
то отримуємо:
y-y>0>=0, z-z>0>=0 (3)
В цьому випадку пряма d паралельна осі Ох ( якщо принаймні одно з чисел y>0>,z>0> відмінно від нуля) або співпадає з віссю Ох (якщо y>0>= z>0>=0).
Рівняння (1), (2), (3) звуться канонічними рівняннями прямої.
Рівняння
прямої, заданої двома точками.
Нехай в просторі обрана афінна система
координат і в цій системі відомі
координати двох точок М>1>
(x>1>,
y>1>,z>1>)
та М>2>
(x>2>,
y>2>,z>2>)
прямої d.
Тоді вектор
є напрямним вектором цієї прямої.
Оскільки вектор
має координати (х>2>-х>1>,
y>2>-y>1>,
z>2>-z>1>),
то канонічне рівняння прямої d
при
згідно формули (1) має вигляд:
(4)
Якщо
одна з координат вектора
або дві його координати дорвінюють
нулю, то для отримання канонічних рівнянь
прямих слід скористатися формулами (2)
та (3).
Приклад.
Нехай у просторі задано дві точки М>1>(1,2,5) та М>2> (4,7,8). Треба скласти рівняння прямої, що проходить крізь ці точки.
Розв’язання. Згідно (4), маємо:
Рівняння
прямої, що задана двома площинами.
Нехай пряма d
є лінією перетину площин
та
, що в декартовій прямокутній системі
координат задані рівняннями:
(5)
Точка
М (x,
y,
z)
належить прямій d
тоді та тільки тоді, коли її координати
є розв’язанням системи рівнянь (5), тому
ця система і є рівнянням прямої d.
Навпаки, будь-яка система рівнянь (5) є
рівнянням деякої прямої простору, якщо
ранг матриці
дорівнює двом.
Для
того, щоб знайти канонічне рівняння
прямої, що задана рівняннями (5) , потрібно
знати координати будь-якої точки М>0>
цієї прямої та деякого направляючого
вектора
.
Точку М>0>
(x>0>,
y>0>,z>0>)
слід обрати так, щоб її координати
задовольняли системі лінійних рівнянь
(5) . Для знаходжння координат направляючого
вектора слід скористатися лемою: якщо
в декартовій системі координат пряма
завдана рівняннями (5), то вектор
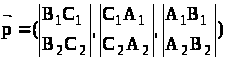є направляючим вектором цієї прямої.
Приклад. Написати канонічне рівняння прямої ,що в декартовій просторовій прямокутній системі координат задана системою рівнянь:
Розв’язання. Спочатку оберемо будь-яку точку на даній прямій. В даному випадку коефіцієнти при х та у не пропорційні, тому надамо z довільне значення, наприклад z>0>=0 та знайдемо з вихідної системи : х>0>=-1, у>0>=-4. Ми знайшли точку М>0> (-1,-4,0), що належить даній прямій.
Координати
напрямного вектора
знайдемо , скористувавшись наведеною
вище лемою:
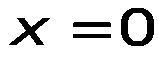або
Таким чином, канонічне рівняння прямої, заданої вихідним рівнянням, має вигляд:
Параметричне рівняння
прямої. Оберем
прямокутну систему координат і задамо
пряму d з
напрямним вектором
та точкою М>0>
(x>0>,
y>0>,z>0>).
Точка М
(x,
y,
z)
простору належить прямій d
тоді та тільки тоді, коли вектори
та
колінеарні, тобто коли існує таке число
t,
що
. Це відношення в координатах запишеться
так:
,
або
(6)
Ці рівності звуться параметричними рівняннями прямої , а t- параметром.
Будь-яку площину у просторі
можна задати точкою, що їй належить М>0>
(x>0>,
y>0>,z>0>)
та направляючим підпростором
,
де
та
два неколінеарних вектори. Будь-яка
точка належить площині тоді та тільки
тоді, коли виконана рівність:
(7)
Розкриваючи по елементах першого стовпчика визначник, отримаємо рівняння площини у вигляді:
Ax+By+Cz+D=0 (8)
де
.
Рівняння (8) є загальним рівнянням площини.
Приклад. Нехай
задано М>0>
(8,-5,6) та
та
.
Треба записати рівняння площини.
Розв’язання. Згідно (8) визначаємо параметри загального рівняння площини:
Таким чином, рівняння площини має вигляд:
-66x-60y-12z+300=0
Умова паралельності та перпендикулярності двох прямих, двох площин, прямої та площини у просторі.
Нехай є дві площини
(9)
З’ясуємо, за яких умов ці площини : а) паралельні; б) перепендикулярні.
Оскільки
A>1>,B>1>,C>1>
–координати вектора
, що перпендикулярний першій площині,
а A>2>,B>2>,C>2>
–координати вектора
, що перпендикулярний другій площині,
то площини паралельні, якщо вектори
,
паралельні, тобто якщо їх координати
пропорціональні:
.
Ця умова разом з тим достатня для паралельності площин ,якщо вони не співпадають.
Для
того, щоб площини (9) були перпендикулярні,
необхідно та достатньо, щоб вказані
вектори
,
були перпендикулярні, що для ненульових
векторів еквівалентно умові:
або А>1>А>2>+
В>1>В>2>+
С>1>С>2>=0.
Приклад. Нехай задано дві площини:
Треба з’ясувати їх взаємне розташування. В даному випадку маємо:
площини не паралельні.
1*2-1*1-2*1=-1
площини не перпендикулярні.
Таким чином, площини розташовані під деяким углом, відмінним від ноля та дев’яноста градусів.
Нехай є площина та пряма, задані рівняннями:
Оскільки вектор
перпендикулярний площині, а вектор
паралельний прямій, то пряма та площина
паралельні, якщо ці вектори перпендикулярні,
тобто якщо
(10)
Якщо при цьому точка ( x>0>, y>0>,z>0>), що належить прямій, задовольняє рівнянню площини
то пряма розташована у площині.
Пряма
та площина перпендикулярні, якщо вектори
та
паралельні, тобто якщо
(11)
Нехай дві прямі задані рівняннями в канонічній формі:
(12)
(13)
Оскільки вектор
паралельний
першій прямій, а вектор
паралельний другій прямій, то прямі
паралельні якщо
Зокрема, прямі співпадають, якщо при цьому точка першої прямої, наприклад (x>0>,y>0>,z>0>) задовольняє рівнянню другої прямої, тобто якщо
.
Прямі перпендикулярні
,якщо вектори
та
перпендикулярні, тобто якщо
Приклад. Нехай задано площину та пряму:
Треба з’ясувати їх взаємне розташування.
Розв’язання. Маємо:
площина та
пряма не паралельні;
площина та
пряма не перпендикулярні.
Таким чином, площина та пряма розташовані у просторі під деяким кутом, відмінним від ноля та дев’яноста градусів.
Дведення координатним методом теореми про три перпендикуляри.
Теорема про три перпендикуляри: якщо пряма, проведена на площині через основу нахилої, перпендикулярна її проекції, то вона перпендикулярна нахилій. І навпаки: якщо пряма на площині перпендикулярна наклонній, то вона перпендикулярна і проекції нахилій.
Доведення.
Нехай АВ- перпендикуляр до площини
,
АС –нахила та с- пряма в площині
, що проходить через основу С нахилої
(малюнок 3). Проведемо пряму
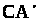, паралельну прямій АВ. Вона перпендикулярна
площині
.
Проведемо через прямі АВ та
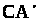площину
. Пряма с перепендикулярна прямій
.
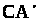Якщо вона перпендикулярна прямій СВ,
то вона перпендикулярна площині
, тобто, і прямій АС.
Аналогічно,
якщо пряма с перпендикулярна похилій
СА то вона, будучи перпендикулярною і
прямій
,
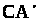перпендикулярна площині
,
а значить, і проекції похилій ВС. Теорему
доведено.
Того ж самого результату можна досягти, якщо скористатись координатним методом, попередньо задавши відповідні прямі їх напрямними векторами та послідовно використовуючи ознаки паралельності та перпендикулярності прямих у просторі.
Малюнок 2- Доведення теореми про три перпендикуляри.
Доведення методом координат ознаки паралельності двох площин.
Нехай
завдані площини
своїми рівняннями:
(14)
(15)
Оскільки
координати загальної точки площин
є розв’язанням системи рівнянь (14),(15)
та кожне розв’язання системи рівнянь
(14),(15) є координатами загальної точки
площин
,
то питання про взаємне розташування
двох площин
зводиться до дослідження системи
лінійних рівнянь (14),(15).
Позначимо через
r
та
відповідно ранги матриць:
Якщо
=2,
r=1, то система рівнянь
(14),(15) несумісна, тому площини
не мають загальних точок, тобто паралельні.
Рівняння сфери. Властивість перетину кулі площиною.
Знайдемо рівняння сфери радіуса r з центром С (a, b, c) в прямокутній системі координат. Точка М простору належить цій сфері тоді та тільки тоді, коли СМ=r або СМ2=r2. Ця рівність в координатах запишеться таким чином:
(16 )
Це – рівняння сфери радіусу r з центром в точці С (a, b, c). Зокрема якщо центр сфери співпадає з початком координат, то a=b=c=0, тому рівність ( 16 ) набуває вигляду :
(17 )
Рівняння (16) можна записати у вигляді :
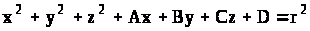(18 )
де
Таким чином, рівняння
будь- якої сфери в прямокутній системі
координат має вигляд (18 ). За аналогією
з колом можна довести, що якщо коефіцієнти
рівняння (18) задовольняють нерівності
,
то поверхня, задана цим рівнянням є
сфера з центром
та радіусом
.
Перетин кулі
площиною є коло- основна властивість
перетинів кулі площиною.
Висновки
При написанні курсової роботи при розгляді питань широко використовувався метод координат. Були розглянуті питання прямої та площини у просторі, умови взаємного розташування прямої та площини, умови паралельності та перпендикулярності прямих та площин.
Список використаної літератури
Атанасян Л.С.,Базылев В.Т. Геометрия. В 2-х ч.. Ч.1.- М.: Просвещение,1986.-336 с.
2.Погорелов А.В. Геометрия.-М.:Наука,1983.-288 с.
Атанасян Л.С., Атанасян В.А. Сборник задач по геометрии, ч.1.-М.:Просвещение,1974.
Мальцев А.И. Основы линейной алгебры.-М.: Наука,1970.