Законы распределения случайных величин. Доверительный интервал

Контрольная работа по дисциплине:

Теория вероятностей и математическая статистика

Законы распределения случайных величин. Доверительный интервал

Задача 1

Вероятность появления события в каждом из независимых испытаний равна 0,8. Найти вероятность того, что в 100 испытаниях событие появится не менее 70 и не более 80 раз.

Решение:

,

где - функция Лапласа, значения которой находятся из таблиц.

;

.

Здесь: .

.

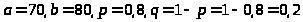Ответ: 0,49.

Задача 2

Среднее число вызовов, поступающих на АТС на 1 минуту, равно двум. Найти вероятность того, что за 4 минуты поступит: а) 3 вызова; б) не менее 3-х вызовов; в) менее 3-х вызовов. Предполагается, что поток вызовов – простейший.

а) Вероятность события «за 4 минуты поступило 3 вызова равна:

,

где

- среднее число вызовов в минуту; ;

t – время, за которое может поступить 3 вызова; t=4 мин.;

k – число возможных вызовов за время t; k=3.

.

- находим из таблицы значений функции распределения Пуассона для k=3 и a==8.

в) События «поступило менее 3-х вызовов» и «поступило не менее 3-х вызовов» являются противоположными. Поэтому найдем сначала вероятность первого события:

.

Здесь: вероятности находятся из таблиц распределения Пуассона соответственно для значений k=0, k=1, k=2 и для a==8.

б) Данное событие является противоположным к событию, описанному в пункте в) (выше), поэтому: .

Ответ: а) 0,03; б) 0,99; в) 0,01.

Задание 3

Случайная величина Х задана функцией распределения (интегральной функцией) f(x). Требуется: а) найти дифференциальную функцию f(x) (плотность вероятности); б) найти математическое ожидание и дисперсию Х; в) построить графики функций f(x) и f(x).

Решение:

а) - плотность вероятности.

б) Математическое ожидание:

.

Дисперсия величины Х:

в) График функции f(x):

х		1	2
f(х)			1

; ; .

График функции

х	1	2
f(х)		1

; .

Задание 4

Найти доверительный интервал для оценки математического ожидания Q нормального распределения с надежностью , зная выборочную среднюю , объем выборки n и среднее квадратическое отклонение .

; ; n=225.

Решение:

.

Здесь: находится из таблицы распределения Стьюдента для n=225 и .

.

;

.

Ответ: (73,12; 77,04).