Жизнь и деятельность семьи Бернулли

Федеральное агентство по образованию РФ

Государственное образовательное учреждение

высшего профессионального образования

Тульский государственный университет

Кафедра математического моделирования

Контрольно-курсовая работа

по курсу

«История и методология механики»

на тему

«Жизнь и деятельность семьи Бернулли»

Тула 2009

Оглавление

Введение

Якоб Бернулли

Иоганн Бернулли

Даниил Бернулли

Якоб II Бернулли

Математические объекты, названные в честь членов семьи

Дифференциальное уравнение Бернулли

Закон Бернулли

Лемниската Бернулли

Неравенство Бернулли

Распределение Бернулли

Числа и многочлены Бернулли

Список литературы

Введение

Семейство Бернулли было одним из протестантских семей, которые из Антверпена в 1583 году, чтобы избежать избиения католиками. Семейство нашло убежище сначала во Франкфурте, а вскоре перебралось в Швейцарию, где осело в Базеле. Основатель династии женился на представительнице одного из самых старинных семейств Базеля и стал крупным купцом. Николай Старший также был крупным купцом. Три поколения Бернулли дали 8 крупных математиков и физиков, из которых наиболее известны Якоб, Иоганн, Даниил и Якоб II. Среди академиков Петербургской Академии наук – пятеро представителей семьи Бернулли. Ниже приведено генеалогическое древо семейства Бернулли.

010009000003d800000001009600000000009600000026060f002201574d464301000000000001004c390000000001000000000100000000000000010000010000006c0000000000000000000000ffffffffffffffff0000000000000000e0360000a629000020454d46000001000001000009000000010000000000000000000000000000007f120000771a0000c80000001f010000000000000000000000000000000f030058600400160000000c000000180000000a0000001000000000000000000000000900000010000000f50c0000d9090000250000000c0000000e00008046000000280000001c0000004744494302000000fffffffffffffffff60c0000da090000000000004600000014000000080000004744494303000000250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c026c01e001040000002e0118001c000000fb020200010000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d010000030000000000

Якоб Бернулли

Якоб родился в семье преуспевающего фармацевта Николая Бернулли. Вначале учился богословию, но увлёкся математикой, которую изучил самостоятельно. В 1677 году совершил поездку во Францию для изучения идей Декарта, затем в Нидерланды и Англию, где познакомился с Гуком и Бойлем.

Вернувшись в Базель, некоторое время работал частным учителем. В 1684 году женился на Юдит Штупанус, у них родились сын и дочь.

С 1687 года – профессор физики (позже – математики) в Базельском университете. В 1684 штудирует первый мемуар Лейбница по анализу и становится восторженным адептом нового исчисления. Пишет письмо Лейбницу с просьбой разъяснить несколько тёмных мест. Ответ он получил только спустя три года (Лейбниц тогда был в командировке в Париже); за это время Якоб Бернулли самостоятельно освоил дифференциальное и интегральное исчисление, а заодно приобщил к нему брата Иоганна. По возвращении Лейбниц вступает в активную и взаимно-полезную переписку с обоими. Сложившийся триумвират – Лейбниц и братья Бернулли – 20 лет возглавлял европейских математиков и чрезвычайно обогатил новый анализ. В 1699 оба брата Бернулли избраны иностранными членами Парижской Академии наук.

Первое триумфальное выступление молодого математика относится к 1690 году. Якоб решает задачу Лейбница о форме кривой, по которой тяжелая точка опускается за равные промежутки времени на равные вертикальные отрезки. Лейбниц и Гюйгенс уже установили, что это полукубическая парабола, но лишь Якоб Бернулли опубликовал доказательство средствами нового анализа, выведя и проинтегрировав дифференциальное уравнение. При этом впервые появился в печати термин «интеграл».

Якоб Бернулли внёс огромный вклад в развитие аналитической геометрии и зарождение вариационного исчисления. Его именем названа лемниската Бернулли. Он исследовал также циклоиду, цепную линию, и особенно логарифмическую спираль. Последнюю из перечисленных кривых Якоб завещал нарисовать на своей могиле; к сожалению, по невежеству там изобразили спираль Архимеда. Согласно завещанию, вокруг спирали выгравирована надпись на латыни, «EADEM MUTATA RESURGO» («изменённая, я вновь воскресаю»), которая отражает свойство логарифмической спирали восстанавливать свою форму после различных преобразований.

Якобу Бернулли принадлежат значительные достижения в теории рядов, дифференциальном исчислении, теории вероятностей и теории чисел, где его именем названы «числа Бернулли».

Он изучил теорию вероятностей по книге Гюйгенса «О расчётах в азартной игре», в которой ещё не было определения и понятия вероятности (её заменяет количество благоприятных случаев). Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей и сформулировал первый вариант закона больших чисел. Якоб Бернулли подготовил монографию в этой области, однако издать её не успел. Она была напечатана посмертно, в 1713 году, его братом Николаем, под названием «Искусство предположений». Это содержательный трактат по теории вероятностей, статистике и их практическому применению, итог комбинаторики и теории вероятностей XVII века. Имя Якоба носит важное в комбинаторике распределение Бернулли.

Якоб Бернулли издал также работы по различным вопросам арифметики, алгебры, геометрии и физики.

Иоганн Бернулли

Иоганн стал магистром (искусств) в 18 лет, перешёл на изучение медицины, но одновременно увлёкся математикой (хотя медицину не бросил). Вместе с братом Якобом изучает первые статьи Лейбница о методах дифференциального и интегрального исчисления, начинает собственные глубокие исследования.

В 1691 будучи во Франции, пропагандирует новое исчисление, создав первую парижскую школу анализа. По возвращении в Швейцарию переписывается со своим учеником маркизом де Лопиталем, которому оставил содержательный конспект нового учения из двух частей: исчисление бесконечно малых и интегральное исчисление.

В качестве концептуальной основы действий с бесконечно малыми Иоганн сформулировал в начале лекций три постулата (первая попытка обоснования анализа):

Величина, уменьшенная или увеличенная на бесконечно малую величину, не уменьшается и не увеличивается.

Всякая кривая линия состоит из бесконечно многих прямых, которые сами бесконечно малы.

Фигура, заключенная между двумя ординатами, разностью абсцисс и бесконечно малым куском любой кривой, рассматривается как параллелограмм.

Позже Лопиталь при издании своего учебника отбросил 3-й постулат как излишний, вытекающий из первых.

В этом же 1691 г. появился первый печатный труд Иоганна в Acta Eruditorum: он нашёл уравнение «цепной линии» (из-за отсутствия в то время показательной функции построение выполнялось через логарифмическую функцию). Одновременно подробное исследование кривой дали Лейбниц и Гюйгенс.

В 1692 им получено классическое выражение для радиуса кривизны кривой.

С 1693 подключился к переписке брата с Лейбницем.

В 1694 женился и в том же году защитил докторскую диссертацию по медицине. В ответ на письмо Лопиталя сообщает ему метод раскрытия неопределённостей, известный сейчас как «правило Лопиталя».

Печатает в Acta Eruditorum статью «Общий способ построения всех дифференциальных уравнений первого порядка». Здесь появились выражения «порядок уравнения» и «разделение переменных» – последним термином Иоганн пользовался еще в своих парижских лекциях. Выражая сомнение в сводимости любого уравнения к виду с разделяющимися переменными, Иоганн предлагает для уравнений первого порядка общий прием построения всех интегральных кривых при помощи изоклин в определяемом уравнением поле направлений. В 1695 по рекомендации Гюйгенса становится профессором математики в Гронингене.

В 1696 Лопиталь выпускает в Париже под своим именем первый в истории учебник по математическому анализу: «Анализ бесконечно малых для исследования кривых линий» (на французском языке), в основу которого была положена первая часть конспекта Бернулли. Значение этой книги для распространения нового учения трудно переоценить – не только потому, что она была первой, но и благодаря ясному изложению, прекрасному слогу, обилию примеров. Как и конспект Бернулли, учебник Лопиталя содержал множество приложений; собственно, они занимали львиную долю книги – 95%. Практически весь изложенный Лопиталем материал был почерпнут из работ Лейбница и Иоганна Бернулли (авторство которых в общей форме было признано в предисловии). Кое-что, впрочем, Лопиталь добавил и из своих собственных находок в области решения дифференциальных уравнений. Объяснение этой необычной ситуации – в материальных затруднениях Иоганна после женитьбы.

Двумя годами ранее, в письме от 17 марта 1694 г. Лопиталь предложил Иоганну ежегодную пенсию в 300 ливров, с обещанием затем ее повысить, при условии, что Иоганн возьмет на себя разработку интересующих его вопросов и будет сообщать ему, и только ему, свои новые открытия, а также никому не пошлет копии своих сочинений, оставленных в свое время у Лопиталя. Этот необычный контракт пунктуально соблюдался 2 года, до издания книги Лопиталя. Позднее Иоганн Бернулли – сначала в письмах к друзьям, а после смерти Лопиталя (1704) и в печати – стал защищать свои авторские права.

Книга Бернулли-Лопиталя имела оглушительный успех у самой широкой публики, выдержала четыре издания (последнее – в 1781 году), обросла комментариями, была даже (1730) переведена на английский, с заменой терминологии на ньютоновскую (дифференциалов на флюксии и т.п.). В Англии первый общий учебник по анализу вышел только в 1706 г. (Диттон).

В 1696 Иоганн публикует задачу о брахистохроне: найти форму кривой, по которой материальная точка быстрее всего скатится из одной заданной точки в другую. Ещё Галилей размышлял на эту тему, но ошибочно полагал, что брахистохрона – дуга окружности. Это была первая в истории вариационная задача, и математики с ней блестяще справились. Иоганн сформулировал задачу в письме Лейбницу, который тотчас её решил и посоветовал выставить на конкурс. Тогда Иоганн опубликовал её в Acta Eruditorum. На конкурс пришли три решения, все верные: от Лопиталя, Якова Бернулли и (анонимно опубликовано в Лондоне без доказательства) от Ньютона. Кривая оказалась циклоидой. Своё собственное решение Иоганн тоже опубликовал.

В 1699 вместе с Якобом избран иностранным членом Парижской Академии наук. В 1702 совместно с Лейбницем открыл приём разложения рациональных дробей на сумму простейших. В 1705 вернулся в Базельский университет, профессором греческого языка.

В 1708 после смерти брата Якоба (1705) приглашается на его кафедру в Базеле и занимает её до самой смерти (1748).

Другими научными заслугами Иоганна Бернулли являются постановка классической задачи о геодезических линиях и нахождение характерных геометрических свойств этих линий, а позднее вывод их дифференциальное уравнение. Необходимо также отметить, что он воспитал множество учеников, среди которых – Эйлер и Даниил Бернулли.

К его портрету Вольтер написал четверостишие:

Его ум видел истину,

Его сердце познало справедливость.

Он – гордость Швейцарии

И всего человечества.

В честь Якоба и Иоганна Бернулли назван кратер на Луне.

Даниил Бернулли

Даниил родился в Гронингене (Голландия), где его отец тогда преподавал математику в университете. С юных лет увлёкся математикой, вначале учился у отца и брата Николая, параллельно изучая медицину. После возвращения в Швейцарию подружился с Эйлером. В 1721 сдал экзамены на медика в Базеле, защитил диссертацию. Затем уехал в Италию, где набирался опыта в медицине. В 1724 выпустил «Математические этюды», принесшие ему известность. В 1725 вместе с братом Николаем уезжает по приглашению в Петербург, где по императорскому указу учреждена Петербургская академия наук. Занимается там медициной, но потом переходит на кафедру математики (1728), ставшую вакантной после смерти его брата Николая. Момент для приезда был чрезвычайно неудачным – как раз скончался Пётр I, началась неразбериха. Приглашённые в Академию иностранцы частично рассеялись, но Даниил остался и даже уговорил приехать друга Эйлера (1727). Но тут умерла императрица Екатерина I, и властям окончательно стало не до Академии. Вскоре Даниил возвращается в Базель. Он остался почётным членом Петербургской академии, в её журнале опубликованы 47 из 75 трудов Даниила Бернулли.

В 1728 напечатал «Замечания о рекуррентных последовательностях». В 1733 устроился профессором анатомии и ботаники в Базеле (других вакансий не было). Ведёт оживлённую, взаимно-полезную переписку с Эйлером. В 1738 как результат многолетних трудов выходит фундаментальный труд «Гидродинамика». Среди прочего там основополагающий «закон Бернулли». Дифференциальных уравнений движения жидкости в книге ещё нет (их установил Эйлер в 1750-е годы).

В течение 1747–1753 выходит в свет важная серия работ о колебаниях струны. Бернулли, исходя из физических соображений, догадался разложить решение в тригонометрический ряд. Он провозгласил, что этот ряд не менее общий, чем степенной. Эйлер и Даламбер выступили с возражениями. Вопрос был решён только в XIX веке, и Бернулли оказался прав.

В 1748 избран иностранным членом Парижской Академии наук. В 1750 перешёл на кафедру физики Базельского университета, где и трудился до кончины в 1782 году. Умер за рабочим столом весной 1782 года.

Женат не был. Отношения с отцом колебались от натянутых до враждебных, споры между ними о приоритете не утихали.

Более всего Даниил Бернулли прославился трудами в области математической физики и теории дифференциальных уравнений – его считают, наряду с Даламбером и Эйлером, основателем математической физики.

Физик-универсал, он основательно обогатил кинетическую теорию газов, гидродинамику и аэродинамику, теорию упругости и т.д. Он первый выступил с утверждением, что причиной давления газа является тепловое движение молекул. В своей классической «Гидродинамике» он вывел уравнение стационарного течения несжимаемой жидкости (уравнение Бернулли), лежащее в основе динамики жидкостей и газов. С точки зрения молекулярной теории он объяснил закон Бойля-Мариотта.

Бернулли принадлежит одна из первых формулировок закона сохранения энергии (живой силы, как тогда говорили), а также (одновременно с Эйлером) первая формулировка закона сохранения момента количества движения (1746). Он много лет изучал и математически моделировал упругие колебания, ввёл понятие гармонического колебания, дал принцип суперпозиции колебаний.

В математике опубликовал ряд исследований по теории вероятностей, теории рядов и дифференциальным уравнениям. Он первый применил математический анализ к задачам теории вероятностей (1768), до этого использовались только комбинаторный подход. Бернулли продвинул также математическую статистику, рассмотрев с применением вероятностных методов ряд практически важных задач.

Даниил являлся Академиком и почетным иностранным членом Петербургской академии наук(1733), членом Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750). Лауреат многочисленных премий и призов в конкурсах.

Якоб II Бернулли

Якоб получил юридическое образование, но затем переключился на физику и математику. После неудачной попытки занять кафедру физики в Базеле, освободившуюся после смерти Даниила Бернулли (1782), Якоб уехал в Италию и поступил на дипломатическую службу. В 1786 году он переселился в Россию. Женился на внучке Эйлера. Служил в Академии наук и Кадетском корпусе. Погиб в возрасте 30 лет в результате несчастного случая при купании в Неве.

Якоб Бернулли успел опубликовать незаурядные работы по различным вопросам механики, теории упругости, гидростатики и баллистики: вращательному движению тела, укрепленного на растяжимой нити, течению воды в трубах, гидравлическим машинам. Вывел дифференциальное уравнение колебания пластин.

Математические объекты, названные в честь членов семьи

Дифференциальное уравнение вида:

_>>с, n≠1, 0.

называется дифференциальным уравнением Бернулли (в честь Якоба).

Метод решения:

1. Делим левую и правую части на yⁿ

_>>

2. Выполняем замену

_>> _>>

3. Решаем дифференциальное уравнение

_>>

Оно может быть решено с использованием интегрирующего множителя

_>>

Пример:

_>>

Делим на y²

_>>

Замена переменных

_>>

Умножаем на M(x),

_>>

Результат

_>>

Закон Бернулли

Закон Бернулли (в честь Даниила Бернулли) является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

_>>

Здесь

ρ – плотность жидкости,

v – скорость потока,

h – высота, на которой находится рассматриваемый элемент жидкости,

p – давление.

Константа в правой части обычно называется напором, или полным давлением, а также интегралом Бернулли. Размерность всех слагаемых – единица энергии, приходящейся на единицу объёма жидкости. Для горизонтальной трубы h = 0 и уравнение Бернулли принимает вид:

_>>

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности ρ:

_>>

Согласно закону Бернулли полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового (ρgh), статического (p) и динамического (_>>) давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров, водо- и пароструйных насосов.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы. На самом деле экспериментально установлено, что скорость жидкости на поверхности твердого тела всегда в точности равна нулю.

Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда.

Согласно закону Бернулли приравняем полные давления на верхней поверхности жидкости и на выходе из отверстия:

_>>

где

p_>0> – атмосферное давление,

h – высота столба жидкости в сосуде,

v – скорость истечения жидкости.

Отсюда: _> >. Это – формула Торричелли. Она показывает, что при истечении идеальной несжимаемой жидкости из отверстия в широком сосуде жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты h.

Для сжимаемого идеального газа

_>>(постоянна вдоль линии тока или линии вихря)

где

_>> – адиабатическая постоянная газа

p – давление газа в точке

ρ – плотность газа в точке

v – скорость течения газа

g – ускорение свободного падения

h – высота относительно начала координат

При движении в неоднородном поле gz заменяется на потенциал гравитационного поля.

Термодинамика закона Бернулли

Выведем закона Бернулли из уравнения Эйлера и термодинамических соотношений.

1. Запишем Уравнение Эйлера:

_>>

φ – потенциал. Для силы тяжести φ=gz

2. Запишем выражение для энтальпии и предположим, что энтропия системы постоянна (или, можно сказать, что течение адиабатично):

dW = VdP + TdS

Пусть S = const и w – энтальпия единицы массы, тогда:

_>> или _>>

3. Воспользуемся следующими соотношениями из векторной алгебры:

_>>

_>>– проекция градиента на некоторое направление равно производной по этому направлению.

4. Уравнение Эйлера с использованием соотношений выведенных выше:

_>>

Спроецируем это уравнение на единичный вектор касательный к линии тока, учитывая следующее:

_>>– условие стационарности

_>>– так как _> >

Получаем:

_>>

То есть на линиях тока в стационарной адиабатической жидкости выполняется следующее соотношение:

_>>

Лемниската Бернулли

Лемниската по форме напоминает восьмёрку. Её название восходит к античному Риму, где «лемнискатой» называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх. Эту лемнискату называют в честь швейцарского математика Якоба Бернулли, положившего начало её изучению.

Уравнения

Рассмотрим простейший случай: если расстояние между фокусами 2c, расположены они на оси OX, и начало координат делит отрезок между ними пополам, то следующие уравнения задают лемнискату:

в прямоугольных координатах:

_>>

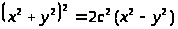в полярных координатах

_>>

Параметрическое уравнение в прямоугольной системе:

_>>,

Чтобы задать лемнискату по двум произвольным точкам, можно не выводить уравнение заново, а определить преобразование координат, при котором старый (данный) фокусный отрезок переходит в новый, и воздействовать на представленные уравнения этим преобразованием.

Свойства.

Лемниската – кривая четвёртого порядка.

Она имеет две оси симметрии: прямая, на которой лежит F_>1>F_>2>, и серединный перпендикуляр этого отрезка, в простейшем (данном) случае – ось OY.

Точка, где лемниската пересекает саму себя, называется узловой или двойной точкой.

Кривая имеет 2 максимума и 2 минимума. Их координаты:

_>>

Расстояние от максимума до минимума, находящихся по одну сторону от серединного перпендикуляра (оси OY в данном случае) равно расстоянию от максимума (или от минимума) до двойной точки.

Касательные в двойной точке составляют с отрезком F_>1>F_>2> углы_>>.

Лемнискату описывает окружность радиуса_>>, поэтому иногда в уравнениях производят эту замену.

Инверсия относительно окружности с центром в двойной точке, переводит лемнискату Бернулли в равнобочную гиперболу.

Для представления в полярных координатах, верно следующее

Площадь полярного сектора _> >, при _> >: _> >

В частности, площадь каждой петли _> >.

Радиус кривизны лемнискаты есть_>>

Построение лемнискаты

с помощью трёх отрезков

Это один из наиболее простых и быстрых способов, однако требует наличия дополнительных приспособлений.

На плоскости выбираются две точки – A и B – будущие фокусы лемнискаты. Собирается специальная конструкция из трёх скреплённых в ряд на шарнирах отрезков, чтобы полученная линия могла свободно изгибаться в двух местах (точки сгиба – C и D). При этом необходимо соблюсти пропорции отрезков: AC=BD=_>>, CD=AB. Края линии крепятся к фокусам. При непараллельном вращении отрезков вокруг фокусов середина центрального отрезка опишет лемнискату Бернулли.

при помощи секущих (способ Маклорена)

Строится окружность радиуса _> >с центром в одном из фокусов. Из середины O фокусного отрезка строится произвольная секущая OPS (P и S – точки пересечения с окружностью), и на ней в обе стороны откладываются отрезки OM_>1> и OM_>2>, равные хорде PS. Точки M_>1>, M_>2> лежат на разных петлях лемнискаты.

Неравенство Бернулли

Неравенство Бернулли (названо в честь Иоганна) утверждает: если_>>, то

_>>

Доказательство проводится методом математической индукции по n. При n = 0 неравенство, очевидно, верно. Допустим, что оно верно для n, докажем его верность для n+1:

_>>, ч.т.д.

Примечания:

Неравенство справедливо также для вещественных _> > (при_>>)

Неравенство также справедливо для _> > (при_>>), но указанное выше доказательство по индукции в случае _> >не работает.

Распределение Бернулли

Распределение Бернулли (названо в честь Якоба) моделирует случайный эксперимент произвольной природы, когда заранее известна вероятность успеха или неудачи.

Случайная величина X имеет распределение Бернулли, если она принимает всего два значения: 1 и 0 с вероятностями p и _> >соответственно. Таким образом:

P (X = 1) = p

P (X = 0) = q

Принято говорить, что событие {X = 1} соответствует «успеху», а {X = 0} «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.

E[X] = p,

D[X] = pq.

Вообще, легко видеть, что

E[_>>] = p _> >.

Числа и многочлены Бернулли

Числа Бернулли – последовательность рациональных чисел B_>0>, B_>1>, B_>2>,… найденная Якобом Бернулли в связи с вычислением суммы одинаковых степеней натуральных чисел:

_>>

Для чисел Бернулли существует следующая реккурентная формула: _> >

Первые четырнадцать чисел Бернулли равны:

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
>>	1	>>	>>	0	>>	0	>>	0	>>	0	>>	0	>>	0	>>

Свойства

Все числа Бернулли с нечетными номерами, кроме B_>1>, равны нулю, знаки B_>2>_>n> чередуются.

Числа Бернулли являются значениями при x = 0 многочленов Бернулли _> >,_>>и равны: B_>n> = B_>n>(0).

Коэффициентами разложения некоторых элементарных функций в степенные ряды часто служат числа Бернулли. Например:

Экспоненциальная производящая функция для чисел Бернулли:

_>>,

_>>

_>>

Эйлер указал на связь между числами Бернулли и значениями дзета-функции Римана ζ(s) при четных s = 2m:

_>>

Из чего следует

B_>n> = − nζ (1 − n) для всех n.

_>>

Список литературы

Белл Э.Т. Творцы математики. М.: Просвещение, 1979.

Боголюбов А.Н. Математики. Механики. Биографический справочник. Киев: Наукова думка, 1983.

История математики. Под редакцией Юшкевича А.П. в трёх томах. Том 3 Математика XVIII столетия. М.: Наука, 1972.