Диференціальні рівняння вищих порядків

ВІННИЦЬКИЙ ФІНАНСОВО-ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ

Кафедра економічної кібернетики

ЗВІТ

з навчальної практики на тему:

«Диференціальні рівняння вищих порядків»

Вінниця 2009

Зміст

Вступ

Диференціальне рівняння вищого порядку

Геометричне тлумачення задачі Коші

Зниження порядку диференціальних рівнянь другого порядку

Диференціальні рівняння є однорідними відносно функції у та її похідних і

Лінійні диференціальні рівняння другого порядку

Питання для перевірки

Тестові завдання

Задачі

Відповіді на тестові завдання

Розв’язок до задач

Охорона праці

Висновки

Література

Вступ

Для успішної участі у сучасному суспільному житті особистість повинна володіти певними прийомами математичної діяльності та навичками їх застосувань до розв’язання практичних задач. Певної математичної підготовки і готовності її застосовувати вимагає і вивчення багатьох навчальних предметів. Значні вимоги до володіння математикою у розв’язанні практичних задач ставлять сучасний ринок праці, отримання якісної професійної освіти, продовження освіти на наступних етапах. Тому одним з головних завдань цього тренінгу є забезпечення умов для досягнення кожним студентом практичної компетентності.

Прикладна спрямованість математичної освіти суттєво підвищується завдяки впровадженню комп’ютерів у навчання математики, повноцінному введенню ймовірносно-статистичної змістової лінії.

Мета: придбання знань, вмiнь та навичок, необхiдних для розв’язання та обчислення диференціальних рівнянь вищих порядків.

Завдання:

вивчення класичних і сучасних наближених методів розв’язання диференціальних рівнянь та їх систем;

придбання умінь використання методів розв’язання задач з початковими умовами та крайових задач для звичайних диференціальних рівнянь та диференціальних рівнянь з частинними похідними при моделюванні систем.

Студент повинен знати:

класифікацію наближених методів розв’язування диференціальних рівнянь та їх систем;

методи розв’язування трансцендентних, алгебраїчних і диференціальних рівнянь та їх систем;

методи чисельного інтегрування і диференціювання.

Студент повинен вміти: самостійно вибирати і обґрунтовувати раціональний метод розв’язування поставленої задачі.

Диференціальне рівняння вищого порядку

Диференційні рівняння вищого порядку стосовно функції у(х) має вигляд:

(1)

яке називають диференційованим рівнянням першого порядку, якщо рівняння (1) подано у вигляді:

(2)

та його називають диференційованим рівнянням першого порядку, яке є розв’язком відносно найстаршої похідної, або явним диференціальним рівнянням, або нормальним диференційованим рівнянням першого порядку.

Оскільки теоретичні поняття і методи інтегрування диференціальних рівнянь вищого порядку є споріднені для рівнянь різних порядків, то надалі ми обмежемось розглядом диференціальних рівнянь другого порядку:

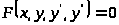(3)

(4).

Функція називається розв’язком диференціального рівняння (3)чи (4) проміжну (a,b), якщо вона двічі не перервно диференційованa на цьому проміжку і будучи підставлена у рівняння, перетворює його у тотожність, тобто

x є (a,b)

або

Графік функції називається при цьому інтегральною кривою диференціального рівняння (3) чи (4).

Зрозуміло, що інтегральна крива повинна міститися в області визначення функції F.

Наприклад, розв’язком диференційованого рівняння є функція на проміжку , бо ця функція є двічі диференційована на цьому проміжутку і Крім того, функція де C_>1,>C_>2>- довільні сталі, є також розв’язком цього рівняння.

Аналогічно переконаємось, що функція і є розвязками диференціального рівняння на проміжку , бо вони двічі диференційовані на цьому проміжку

Розвязком цього рівняння є також функції де - довільні сталі.

Далі будемо розглядпти основні поняття та означення для диференціального рівняння (4).

Функція де і довільні сталі називається загальним розв’язком диференційованого рівняння другого порядку, якщо вона є розв’язком цього рівняння для розв’язком функції і і з якої за рахунок вибору значень цих сталих можна отримати будь-який розв’язок цього рівняння (за винятком може окремих).

Розвязок який отримуємо із загального диференціального рівняння 2-го порядку, мадаючи і певних числових значень, називається числовим розвязком цього рівняння.

Задача Коші. Практичних задач, які зводяться до диференціального рівняння другого порядку, потрібно відшукати розвязок цього рівняння, що задовольняє певні додаткові умови.

Найчастіше ними є умови Коші:

(5)

Задача знаходження розвязку диференціального рівняння (4), який задовольняє умови (5), називається задачею Коші для цього рівняння. Цю задачу Коші записуватимемо коротко:

Геометрично, задача Коші для диференціального рівняння (4) полягає у знаходженні інтегральної кривої цього рівняння. Яке проходить через точку і яка дотикається у цій точці до вектора, що утворює кут y, з додатним напрямком осі

Геометричне тлумачення задачі Коші

Зрозуміло, що точки повинні лежати області визначення функції , тобто області визначення диференціального рівняння (4).

Можна показати, що правильне таке твердження: якщо функція та її частинні похідні і є неперервні в деякому околі точки , то існує єдиний розв’язок задачі Коші (4) – (5), який визначений у певному околі точки .

Геометрично це означає, що при виконанні умов сформульованої теореми, через точну проходить єдина інтегральна крива диференціального рівняння (4), яка замикається у цій точці до вектора, який утворює з додатним напрямом осі 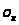кут .

З теореми існування та розв’язку задачі Коші для рівняння (4) випливає, що при виконанні умов теореми в деякому околі точки існує загальний розв’язок цього рівняння, з розв’язком якого отримати розв’язок задачі Коші, визначивши значення сталих і із системи рівнянь:

(6)

Відзначемо, що система рівняння (6) завжди є розв’язком, бо існує розв’язок задачі Коші (4) – (5)

На практиці для диференціального рівняння другого порятку можуть бути задані інші умови замість умов Коші. Ними можуть бути крайові умови: і геометрична задача полягає у знаходженні інтигральної кривої диференціального рівняння (4), яка проходить через дві точки ,.

Примітка. Якщо диференціального рівняння (3) має один розвязок відносно , то воно рівносильне диференційномурівняню , де

Якщо ж диференціальне рівняння (3) має декілька розв’язком відносно , то воно рівносильне сукупності диференціальних рівнянь.

де

Зниження порядку диференціальних другого порядку

Основним методом інтегрування (знаходження загального розвязку або загального інтеграла) диференціальних рівнянь вищого порядку є зниження їх порядку і зведення до інтегрування диференціальних рівнянь першого порятку. Розглянемо деякі можливі видатки зниження порядку диференціальних рівнянь другого порядку.

Диференціальне рівняння не містить невідомої функції у, тобто має вигляд:

(7).

У цьому випадку робимо заміну і отримуємо диференціальне рівняння першого порядку стосовно невідомої функції Z:

Якщо знайдемо загальний розв’язок , рівнянь (8) то далі інтегруємо рівняння ; якщо ж знайдемо загальний інтеграл то для знаходження розв’язків диференціального рівняння (7) отримуємо наявне диференціальних рівнянь першого порятку

Диференціальне рівняння не містить явно аргументах х, тобто має вигляд

(9)

У розв’язаному випадку приймаємо за невідому функцію а й аргументи вважаємо у. Тоді маємо:

Підставимо вирази для у’,y” у рівняння (9), отримаємо відносно функцію диференціальних рівнянь першого порядку:

(10)

Якщо знайдемо загальний розв’язок рівняння (10), то дані інтнгруєм явне диференціальне рівняння першого порядку яке є з розв’язком функції змінними; якщо ж знайдено загальний інтеграл рівняння (17.10), то дані інтегруємо наявне диференційне рівняння першого порядку.

Диференціальне рівняння (3) є однорідним відносно функції у та її похідних і

тобто

У цьому випадку виконуємо заміну де z = z (x). Знаходимо Підготовимо вирази для та у рівняння (3) і використовуємо його однорідність:

У результаті приходимо до диференціальних рівнянь першого порятку стосовно функції

(11)

яке з точністюдо розвязку рівносильне рівняню (3)

Якщо знайдемо загальний розвязок рівняння (11), то речі інтегруємо розв’язане дифененційне рівняння першого порядку , яке є з відокремлюваними змінними; якщо ж знайдемо загальний інтеграл то приходимо до інтегрування наявного диференціального рівняння першого порядку:

При зниженні порядку вихідного рівняння міг бути втрачений його розв’язок у=0. Але він не втрачений, отримуємо із загального розв’язку при

Лінійні диференціальні рівняння другого порядку

Диференціальні рівняння розв’язку порядку (3) називається лінійним, якщо функція,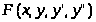є лінійно відносно тобто якщо воно має вигляд

(12)

Будемо вважати, що розв’язком і вільний член q(x) x є(a,b) i .

Якщо то маємо відповідне лінійне однорідне рівняння

(13)

Якщо ,то рівняння (12) називають лінійним не однорідним диференціальним рівняння другого порядку.

Питання для перевірки

Що називається диференціальним рівнянням вищого порядку ?

Задача Коші.

Основні методи інтегрування.

Лінійні диференціальні рівняння другого порядку.

Тестові завдання

1. Диференційні рівняння вищого порядку стосовно функції у(х) має вигляд:

1.

2.

3.

2. Функція (вписати відповідь) де і довільні сталі називається загальним розв’язком диференційованого рівняння другого порядку, якщо вона є розв’язком цього рівняння для розв’язком функції і і з якої за рахунок вибору значень цих сталих можна отримати будь-який розв’язок цього рівняння (за винятком може окремих).

3. Співвідношення яким певно додається загальний розв’язок диференціального рівняння 2-го порядку, називається (вписати відповідь) цього рівняння.

4. Диференціальне рівняння не містить невідомої функції у, тобто має вигляд:

1.

2.

3.

5. Розв’язок який отримуємо із загального диференціального рівняння 2-го порядку, падаючи і певних числових значень, називається числовим (вписати відповідь) цього рівняння.

6. Графік функції називається при цьому (вписати відповідь) диференціального рівняння (3) чи (4).

7. Диференціальні рівняння розв’язку порядку (3) називається лінійним, якщо функція,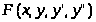є лінійно відносно тобто якщо воно має вигляд

1.

2.

3.

8. Співвідношення … яким певно додається загальний розв’язок диференціального рівняння 2-го порядку, називається загальним інтегралом цього рівняння:

1.

2.

3.

9. З теореми існування та розв’язку задачі Коші для рівняння (4) випливає, що при виконанні умов теореми в деякому околі точки існує загальний розв’язок цього рівняння, з розв’язком якого отримати розв’язок задачі Коші, визначивши значення сталих і із системи рівнянь:

1.

2.

3.

Задачі

Задача 1. Знайти розв’язок диференційoваного рівняння що задовольняє умови

Розв’язання. Загальний розв’язок цього рівняння легко знайти шляхом інтегрування заданої рівності, бо тоді розв’язком функції , друга похідна яких дорівнює 6х:

загальний розв’язок рівняння.

Задача 2. Знайти розв’язок рівняння , який звдовольняє умови: .

Розв’язання. Оскільки у рівнянні явно не входить аргумент х, то знижуємо його порядок підстановкою 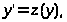з якої випливає, що

Підставити вирази для і , у дане рівняння, отримаємо диференціальне рівняння першого порядку

яке рівносильне сукупності рівнянь:

Інтегруємо друге рівняння, яке є з відокремлюваними змінними:

.

При відокремлені зміних втраченими могли бути розвязки і . Ці розв’язки не є втраченими, бо перший з них співпадає з першим рівнянням сукупності, а другий отримуємо з сімї

при

Отже, множина всіх розв’язкв дискретного рівняння у змінних y i z записується сукупністю розв’язком:

Враховуючи, що з одержаних розв’язків з яких отримуємо дві сукупності диференційних рівнянь:

Одже множина розв’язків вихідного диференціального рівняння складається з двох цілей інтегральних кривих і .

Розв’язок, який задовольняє початкові умови у(1)=1, у’(1)= -1 входить у другу сімю, яка виражається загальним інтегралом . З цього загального інтеграла вилучаємо розвязок, що задовольняє задані початкові умови. Для цього маємо систему рівнянь для визначенняі :

Таким чином, шуканий розв’язок задачі Коші має вигляд:

Задача 3. Проінтегрувати рівняння знаючи, що є розв’язком відповідного однорідного рівняння.

Розв’язання. Приймемо і обчислемо похожі Підставимо вирази для у рівняння:

Після елементарних перетворень отримуємо рівняння:

або

Виконуємо заміну z’=u і маємо лінійне диференціальне рівняння першого порядку

Інтегруємо відповідне однорідне рівняння:

Загальний розв’язок лінійного неоднорідного рівняння стосовно функції u шукаємо у вигляді

Підготовимо цю функцію в неоднорідне рівняння і знайдемоС(х):

Отже, загальний розв’язок лінійного неоднорідного рівняння стосовно функції u записується у вигляді

Врахувавши, що , одержуємо загальний розв’язок

вихідного рівняння.

Задача 4. Розв’яжіть рівняння

Задача 5. Розв’язати рівняння

Відповіді на тестові завдання

1.

2.

3. загальним інтегралом

4.

5. числовим розв’язком

6. інтегральною кривою

7.

8.

9.

Розв’язок до задач

Розв’язання до задачі 4. Дане рівняння не містить невідомої функції, тому приймаємо, що і отримуємо диференціальних рівнянь першого порятку

Інтнгруємо одержане рівняння з відокремлюваними змінними:

Далі інтегруємо рівняння

Прийнявши отримаємо загальний розв’язок рівняння у вигляді

Розв’язання до задачі 5. Дане рівняння є однорідне відносно у,у’,у”, бо

Приймемо, що одержуємо:

Вихідне рівняння з точністю до зводити до рівняння

Одержали для знаходження z лінійне неоднорідне диференційне рівняння першого порядку

Спочатку інтегруємо відповідне однорідне рівняння

Загальний розв’язок неоднорідного рівняння шукаємо методом варіації сталої, тобто у вигляді

Підготовимо цю функцію в неоднорідне рівняння і знайдемо функцію С(х):

Загальний розв’язок лінійного неоднорідного рівняння розв’язком функції z має вигляд

Оскільки , то далі інтегруємо диференціюємо рівняння

Після потенціювання отримуємо загальний розв’язок вихідного рівняння:

Охорона праці. Вентиляція виробничих приміщень

Одним з ефективних засобів нормалізації повітря у приміщенні є вентиляція.

Вентиляція - повітрообмін, завдяки якому забруднене повітря виводиться з приміщення, а замість нього вводиться свіже зовнішнє або очищене повітря.

Задачі вентиляції - забезпечення чистоти повітря та заданих мікрокліматич-них умов.

Вентиляція класифiкується:

1) по засособу переміщення повітря розрізнюють системи природньої, штучної (механічної) та змішаної вентиляції.

2) по напрямку руху повітря - підрозділяються на приточну (повітря подається у приміщення), витяжну (забруднений повітря удаляється з приміщення) та приточно - витяжну.

В залежності від місця дії вентиляція може бути загальнообмінною (використовується коли шкідливі речовини рівномірно розміщуються у робочої зоні), місцевою (- шкідливі речовин виділяються на декількох робочих місцях), локалізованою (- шкідливі речовин виділяються на робочих місцях, розташованих одне біля іншого) та комбiнованою.

Загальнообмінна вентиляція забезпечує створення необхідного мікроклімату та чистоти повітряного середовища у всьому об’ємі робочої зони. При місце-вій вентиляції шкідливі речовини виводяться (або розстворюються шляхом подачі чистого повітря) безпосередньо від місць їх створення.

По призначенню вентиляція може бути робочою (використовується при нормальному режимі роботи технологічних процесів) та аварійною (викорис-товується у випадку, якщо стався викид шкідливих речовин у наслідку аварії).

Вимоги до вентиляції:

1) кiлькiсть приточного повітря у одиницю часу повинне відповідати кiлькості витяжного повітря.

2) правильне розташування приточних та витяжних завіс. Свіже повітря подається, де концентрація шкідливих речовин менше, а удаляється, де концентрація більше.

3) вентиляція не повинна створювати перегрівання або охолодження працюю-чих.

4) вентиляція має бути пожежовибухонебезпечною.

Висновки

Ознайомившись з матеріалом ми можемо навчитися володіти певними прийомами математичної діяльності та навичками їх застосування до розв’язання практичних задач.

Виконавши головні завдання цього трейнінгу ми можемо досягти компетентності в практичні діяльності.

Ми оволоділи уміннями та навичками, необхідними для розв’язання та обчислення диференціальних рівнянь вищих порядків.

Ми вивчили класичні і сучасні методи розв’язання алгебраїчних, трансцендентних, диференціальних рівнянь та їх систем.

Ми навчились використовувати методи розв’язання задач з початковими умовами та крайових задач для звичайних диференціальних рівнянь та диференціальних рівнянь з частинними похідними при моделюванні систем.

Література

1. Ильин В.А., Позняк Э.Г., Аналитическая геометрия. Наука. М. 1978.-302 с.

2. Панков О.А., Панкова Т.Е. Вища математика.ВІРЕУ. 1998.-120с.

3. Булига К.Б., Барановська Л.В. Практикум з теорії ймовірностей та

математичної статистики. – К.: Видавництво Європейського університету, 2000

4. Чубатюк В.М. Вища математика. Навчальний посібник для студентів економічних спеціальностей навчальних закладів III та IV рівнів акредитації.- К.: ВД «Професіонал», 2006.-432 с.

5. Барковський В.В., Барковська Н.В., Математика для економістів. Вища математика.- К.: Н.А.У., 1999.- 428с.