Дискретная математика (работа 3)
Министерство образования и науки
Российской Федерации
Российский химико-технологический университет
им. Д.И. Менделеева
Новомосковский институт
Издательский центр
T.П. Тюрина, В.И. Емельянов
Дискретная математика
(часть 3)
Учебное пособие
Новомосковск 2004
Содержание
Часть 3. Элементы алгебры логики 3
3.1 Введение в алгебру логики 3
3.2 Основные функции алгебры логики 5
3.3 Формулы алгебры логики 9
Контрольные вопросы 12
3.4 Законы алгебры логики и следствия из них 12
Контрольные вопросы 16
3.5 Логические функции многих переменных 16
3.6 Построение формул алгебры логики по заданной таблице истинности 18
Контрольные вопросы и упражнения 26
3.7 Некоторые замкнутые классы (классы Поста). Понятие базиса 26
Контрольные вопросы и упражнения 34
3.8 Методы минимизации логических функций 34
Контрольные вопросы 39
3.9 Неполностью определенные логические функции 40
3.10 Формы представления булевых функций 41
3.10.1 Семантические деревья 42
3.10.2 Бинарные диаграммы решений (БДР) 45
3.11 Построение логических схем 45
Контрольные вопросы 45
3.12 Логические конечные автоматы 46
3.12.1 Процессы 50
3.12.2 Конечные автоматы 52
Контрольные вопросы 55
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 60
Часть 3. Элементы алгебры логики
3.1 Введение в алгебру логики
Алгебру логики иначе еще называют алгеброй высказываний, логикой высказываний. Алгебра логики начала формироваться в 19 веке в трудах английского математика Дж. Буля.
Прежде всего, благодаря труду английского логика Джорджа Буля «Математический анализ логики», был достигнут подлинный прогресс науки, называемый математической логикой. Он перенёс на логику законы и правила математических действий, ввёл логические операции, предложил способ записи высказываний в символической форме.
В трудах Джорджа Буля и О. де Моргана математическая логика представлена как своеобразная алгебра – алгебра логики (алгебра высказываний).
Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Джордж Буль (1815–1864) родился в Линкольне (Англия). Сын сапожного мастера. Окончил только начальную школу и дальнейшие знания приобретал самоучкой. С 1849 г. Буль – профессор математики в Куинс – колледже в Корке (Ирландия), где преподавал до конца жизни. Буля почти в равной степени интересовали логика, математический анализ, теория вероятностей, этика Б. Спинозы, философские работы Аристотеля и Цицерона. Он считается несомненным создателем современной символической (математической) логики.
Огастес де Морган (1806–1871) родился в Индии в семье полковника английских войск. Получил образование в Кембриджском университете. Был профессором математики Лондонского университета. Математику и логику де Морган назвал азами точного знания и выражал сожаление, что математики не более заботятся о логике, чем логики о математике. Сам он стремился сблизить обе науки, и его главной заслугой явилось построение логики по образу и подобию математических наук. Независимо от Дж. Буля он открыл основные идеи алгебры логики.
«Логика Буля» основывается на отношении эквивалентности, при котором правая часть равенства всегда содержит ровно столько же «истин», сколько и левая.
Высказывание – это имеющее смысл языковое выражение (повествовательное предложение), относительно которого в данной ситуации можно утверждать, что оно либо истинно, либо ложно, т. е. каждому высказыванию можно приписать истинное значение И (истина) или Л (ложь), но не то и другое одновременно.
Примеры:
НГТУ – крупнейший «вуз Новосибирска».
«Снег зелёный».
Р= «Чтобы подключиться к Интернету с домашнего компьютера, необходим модем и соответствующее ПО».
Крокодилы летают очень низко.
«А ты любишь информатику?» – это предложение не является высказыванием.
Уравнение 2+х=4 не является высказыванием. Однако, всякий раз, придавая переменной х определенное числовое значение, будем получать высказывание. Используя частицу «не», а также союзы «и», «или», связки «если …., то…», «тогда и только тогда, когда…» и т. п., можно из одних высказываний строить другие высказывания.
Изучением высказываний занимается Булева алгебра, в которой предполагается, что уже имеется некоторый запас высказываний, для каждого из которых известно истинно оно или ложно. Такие высказывания называют элементарными высказываниями. Из элементарных высказываний могут быть построены сложные с помощью операций алгебры логики.
Знаки логических операций называют логическими связками (или просто связками). Логические связки могут быть одноместные (унарные), двухместные (бинарные), трехместные (тернарные) и т. д.
В алгебре логики логические операции чаще всего описываются при помощи таблиц истинности, содержащих все наборы значений переменных и значения функции этих наборов. Алгебра логики не занимается обоснованием того, почему тому или иному элементарному высказыванию приписано значение истины или лжи. Этот вопрос решается за пределами алгебры логики.
Например: сумма углов в треугольнике – 180 градусов. Алгебра логики отвлекается и от смысловой содержательности высказывания. Она интересуется только одним свойством сложных высказываний: быть истинным (True – 1) или ложным (False – 0).
3.2 Основные функции алгебры логики
Основной задачей теории булевых функций является разработка систематического метода построения сложных функций из более простых. Этот метод основан на изучении свойств булевых функций.
Основными символами алгебры высказываний являются:
а) пропозиционные переменные Р1, Р2, Р3, …;
б) одноместная связка – () и двуместные связки (и), (или), , , ;
в) скобки ().
Переменная, значениями которой являются высказывания, называется пропозиционной переменной.
Пусть А, В-некоторые элементарные высказывания.
Определим
новое высказывание Ā
(т. е. не А),
будем называть его отрицанием (инверсия:
 ,
Ā),
представим таблицы значений функции
отрицания:
,
Ā),
представим таблицы значений функции
отрицания:
|
А |
Ā |
|
1 0 |
0 1 |
|
A |
B |
|
0 0 1 1 |
0 1 0 1 |
|
№ |
Обозначение операции |
Другие обозначения |
Набор истинных значений |
Название логической опции и связки |
Как читается |
Арифметическая модель |
|
12 |
АВ |
А+В Max (А, В) |
0 1 1 1 |
Дизъюнкция, логическое сложение, «или» |
А или В |
A+B-AB |
|
23 |
АВ |
А&В АВ Min (А, В) |
0 0 0 1 |
Конъюнкция, логическое умножение «и» |
А и В |
AB |
|
34 |
АВ |
АВ АВ |
1 1 0 1 |
Импликация, логическое следование |
Если А, то В А влечет В |
1 A+ AB |
|
45 |
АВ |
АВ АВ АВ |
1 0 0 1 |
Эквиваленция, эквивалентность |
А тогда и только тогда, когда В; А эквивалентно В |
1 – (A-B)2 |
|
56 |
АВ |
А+В АВ АВ |
0 1 1 0 |
Сумма по модулю 2, сумма Жегалкина |
А плюс В; Либо А, либо В |
|
|
67 |
АВ |
1 1 1 0 |
Штрих Шеффера, антиконъюнкция |
Неверно, что А и В; А штрих Шеффера В |
||
|
78 |
АВ |
АВ АВ |
1 0 0 0 |
Стрелка Пирса, антидизъюнкция, функция Вебба, функция Даггера |
Ни А, ни В; А стрелка Пирса В |
Несмотря на то, что булевых функций от любого заданного числа m двоичных переменных конечное число, их слишком много, чтобы иметь запас преобразователей для любых встретившихся отображений. Рассмотрим сначала все возможные функции от одной двоичной переменной. Их четыре, две из них – константы (0 и 1), одна – тождественная функция и только одна – функция отрицания (функция НЕ) – является нетривиальной.
|
p |
|
|
0 |
1 |
|
1 |
0 |
Очевидно,
что число различных булевых функций от
m
переменных
равно 2 в степени
 .
При m
= 2 это число 16, то есть всего функций от
двух переменных 16, однако наиболее
практически применимых из них меньше.
.
При m
= 2 это число 16, то есть всего функций от
двух переменных 16, однако наиболее
практически применимых из них меньше.
Суперпозиция двоичных функций может быть записана как формула, которую называют логической формулой.
Пример.
Логическая
формула
 задает функцию от трех переменных как
суперпозицию функций одной и двух
переменных.
задает функцию от трех переменных как
суперпозицию функций одной и двух
переменных.
Для
уменьшения числа скобок вводятся
приоритеты операций. Наиболее приоритетна
функция отрицания. Затем идет конъюнкция,
после нее – дизъюнкция. Все другие
функции имеют равный приоритет, меньший,
чем у дизъюнкции. Очевидно, что скобками
можно установить желаемый порядок
операций. Вышеприведенная формула может
быть эквивалентно записана так:
 .
Отметим, что используют и другое
распределение приоритетов, в частности,
полагая импликацию менее приоритетной,
чем все другие функции.
.
Отметим, что используют и другое
распределение приоритетов, в частности,
полагая импликацию менее приоритетной,
чем все другие функции.
Логическая формула дает возможность построить соответствующий функциональный преобразователь, если мы имеем «элементарные» или «базисные» преобразователи. Для реализации преобразователя f примера выше необходимо иметь элементы, реализующие отрицание, дизъюнкцию, конъюнкцию и сложение по модулю два (см. рис. 1).
На этом рисунке представлен пример синтаксической структуры формулы – графическое представление формулы.

Рис. 1.
Синтаксическая структура формулы

Очевидным образом по формуле можно построить табличное представление функции f.
Таблица 2
|
p |
q |
r |
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
Суперпозицией нескольких простых булевых функций можно построить более сложную функцию, в частности, булеву функцию от большего числа переменных. Поставим вопрос: можно ли суперпозицией фиксированного набора функций представить любую булеву функцию от любого числа переменных? Удивительно, но ответ на этот вопрос положителен.
Штрих Шеффера является отрицанием конъюнкции, стрелка Пирса – отрицание дизъюнкции, сумма Жегалкина – отрицание эквивалентности.
М. Жегалкин (1869–1947) – российский математик и логик, один из основоположников современной математической логики.
Чарльз Пирс (1839–1914) – американский логик, математик и естествоиспытатель. Основоположник семиотики, родоначальник прагматизма.
3.3 Формулы алгебры логики
Из логических переменных можно составлять различные конструкции, которые образуют формулы алгебры логики.
Пусть
 – некоторое множество логических
переменных. По индукции определим
понятие формулы алгебры логики:
– некоторое множество логических
переменных. По индукции определим
понятие формулы алгебры логики:
любая логическая переменная является формулой (атомарной);
если
 и
и
 – формулы, то выражения
– формулы, то выражения
 и другие, представленные в табл. 1,
являются формулами;
и другие, представленные в табл. 1,
являются формулами;никаких других формул, кроме построенных в пунктах 1 и 2, нет.
Если
формула
 построена из логических переменных,
лежащих в множестве {x>1>,
x>2>,…,
x>n>},
то будем писать
построена из логических переменных,
лежащих в множестве {x>1>,
x>2>,…,
x>n>},
то будем писать
 {x>1>,
x>2>,…,
x>n>}.
{x>1>,
x>2>,…,
x>n>}.
Таблицы истинности также называются интерпретациями логических операций и составляют семантику формул (т. е. придание смысла формулам) в отличие от синтаксиса формул (т. е. формальных законов их построения, данных в определении формулы).
На
множестве
 вводится транзитивное отношение <
«быть более сильным» и отношение ~ «быть
равносильным» по правилам, представленным
на рис. 2. Для равносильных связок
расстановка скобок выполняется слева
направо.
вводится транзитивное отношение <
«быть более сильным» и отношение ~ «быть
равносильным» по правилам, представленным
на рис. 2. Для равносильных связок
расстановка скобок выполняется слева
направо.

Рис. 2. Приоритетность логических операций
Все формулы алгебры логики можно разделить на 3 класса:
нейтральные, или выполнимые – принимающие как истинное, так и ложное значения;
тождественно истинные формулы (или тавтологии) – принимающие истинные значения при любых значениях переменных;
тождественно ложные формулы – принимающие ложные значения при любых оценках переменных.
Существует два способа определения истинного значения формулы. Первый – с помощью таблиц истинности, а второй – путём приведения формул к нормальной форме. Формула имеет нормальную форму, если в ней отсутствуют знаки эквиваленции, импликации, двойного отрицания и др., при этом знаки отрицания находятся только при переменных.
Табличный способ определения истинного значения формул имеет ограниченное применение, поскольку при увеличении количества переменных приходится рассматривать слишком много вариантов (2N).
Равносильными называются два высказывания, у которых таблицы истинности совпадают.
Пример.
Составим таблицу истинности функции
f=(A B)~(
B)~(
 ):
):
Таблица 3
|
A |
B |
A |
|
|
|
(A |
|
0 0 1 1 |
0 1 0 1 |
1 1 0 1 |
1 1 0 0 |
1 0 1 0 |
1 1 0 1 |
1 1 1 1 |
Полученное
высказывание истинно всегда. Такие
высказывания называют тождественно
истинными и обозначаются J.
По аналогии существуют и тождественно
ложные высказывания L.
Метод заполнения таблицы истинности
принят для не очень сложных высказываний.
Если выражение содержит N
опций, то таблица становится громоздкой.
Для этого используются законы алгебры
логики. Таблицу истинности можно
составить с использованием программы.
В большинстве языков высокого уровня
имеются логические операции NOT,
AND,
OR,
XOR,
реализующие операции
 соответственно.
соответственно.
Контрольные вопросы
1. Дайте определение высказывания.
2. Перечислите основные символы алгебры высказываний.
3. Перечислите основные функции алгебры логики.
4. Что является основной задачей алгебры логики?
5. Что такое таблицы истинности логических функций?
6. Составьте таблицу истинности функций дизъюнкции и конъюнкции.
7. Составьте таблицу истинности функций импликации и эквивалентности.
8. Составьте таблицу истинности функций отрицания и сложения по модулю 2.
9. Составьте таблицу истинности функций Штрих Шеффера и Стрелка Пирса.
10. Формулы алгебры логики. Приоритет логических операций. Какие отношения имеют место на множестве логических операций?
11. Что такое синтаксическая структура формулы?
12. На какие классы делятся формулы алгебры логики?
3.4 Законы алгебры логики и следствия из них
При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре логики производится на основе эквивалентных преобразований, опирающихся на основные логические законы. Законы алгебры логики – это тавтологии (или теоремы).
1. Закон тождества:
А=А
2. Закон непротиворечия:


3. Закон исключения третьего:

4. Закон двойного отрицания:

5. Законы истины и лжи (свойства констант):






6. Законы идемпотентности:


7. Коммутативные законы:


8. Ассоциативные законы:
 – дизъюнкции
– дизъюнкции
 – конъюнкции
– конъюнкции
9. Дистрибутивные законы:
 – 1 ый
дистрибутивный закон
– 1 ый
дистрибутивный закон
 – 2 ой
дистрибутивный закон
– 2 ой
дистрибутивный закон
10. Законы поглощения:


11. Законы де Моргана:


12. Закон импликации:

13. Закон эквивалентности:



14. Свойства сложения «по модулю два»:


Справедливость этих законов можно доказать с помощью таблиц истинности сложных логических связей описываемых законов.
Следствия из законов алгебры логики (часто используются при упрощении логических выражений).
1. Правило поглощения. Данное правило является следствием из дистрибутивного закона. Оно может быть записано в следующем виде:
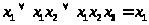 .
.
2. Правило свертки. Правило является следствием из второго дистрибутивного закона. Запись правила:
а)
 ;
;
б)
 .
.
3. Правило расширения. Правило записывается в следующем виде:
 .
.
4.
Правило склеивания. Базируется на
понятии соседних конъюнкций. Соседними
называются конъюнкции, отличающиеся
представлением одной переменной.
Например, конъюнкции
 и
и
 ,
,
 и
и
 являются попарно соседними. В первой
паре конъюнкции отличаются представлением
х>2>,
а во второй – представлением х>1>.
По этим переменным конъюнкции склеиваются.
являются попарно соседними. В первой
паре конъюнкции отличаются представлением
х>2>,
а во второй – представлением х>1>.
По этим переменным конъюнкции склеиваются.
Формулировка правила: две соседние конъюнкции склеиваются с образованием одной конъюнкции меньшего ранга; исчезает та переменная, по которой конъюнкция склеивается.
 ,
,
 .
.
Контрольные вопросы
1. Перечислите основные законы алгебры логики. Как дозывается их справедливость?
2. Перечислите следствия из законов алгебры логики.
3.5 Логические функции многих переменных
Все логические операции, которые были рассмотрены в 3.2, распространяются и на функции нескольких переменных. Теперь будем рассматривать функции F(x>1>, x>2>,…, x>n>), где x>i> – логические переменные, которые принимают значения нуля или единицы. Для описания логики функционирования аппаратных и программных средств компьютера используется алгебра логики, или булева алгебра. Два элемента алгебры логики – ее константы – 0 (ложь) и 1 (истина). Во всех компьютерах используются сигналы двух видов. Сигналы можно интерпретировать как двоичные числа, или логические переменные.
Логической функцией F от набора логических переменных х>1>,…, х>n> называется функция, которая может принимать только два значения: логический 0 и логическая 1.
Область определения логической функции конечна и зависит от количества возможных наборов аргументов. Если n – число аргументов, то количество возможных наборов аргументов равно 2n.
Множество значений функции F(x>1>,…, x>n>) – это множество {0,1}, т. е. F=0 либо 1.
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записываются наборы аргументов, а в правой – соответствующие значения функции.
|
x>1> |
x>2> |
… |
x>n-1> |
x>n> |
F(x>1, >x>2,…>, x>n-1, >x>n>) |
|
0 |
0 |
… |
0 |
0 |
F (0,0,…, 0,0) |
|
0 |
0 |
… |
0 |
1 |
F (0,0,…, 0,1) |
|
0 |
0 |
… |
1 |
0 |
F (0,0,…, 1,0) |
|
… |
… |
… |
… |
… |
… |
|
1 |
1 |
… |
1 |
1 |
F (1,1,…, 1,1) |
Вектором значений булевой функции F(x>1>,…, x>n>) называется упорядоченный набор всех значений функции F, при которых значения упорядочены по лексикографическому порядку множества аргументов {0,1}n.
Поскольку
всего имеется 2n
наборов
 нулей и единиц (|{0,1}n|=2n),
существует ровно
нулей и единиц (|{0,1}n|=2n),
существует ровно
 булевых функций F(x>1>,…,
x>n>)
от n
переменных:
булевых функций F(x>1>,…,
x>n>)
от n
переменных:
 .
.
При n=2 количество функций равно 16, при n=3 – 256 и т. д. На рис. 3 представлены в упорядоченном виде наборы аргументов для ряда функций – отрицания 0, функций одного, двух и трёх аргументов.

Рис. 3. Упорядоченные наборы аргументов
3.6 Построение формул алгебры логики по заданной таблице истинности
Пусть F – двоичная функция от n переменных. Предположим, что F не равна тождественно нулю. Пусть T>1>, T>2>,…, T>k> – все точки ее определения, в которых F=1. Можно доказать, что справедлива следующая формула:
 ,
,
где
 ,
j=1,2,…,
k,
,
j=1,2,…,
k,

Построить функцию F можно и по-другому. Если функция F не равна тождественно единице и S>1>, S>2>,…, S>m> – все точки области ее определения, в которых F=0, то справедлива формула:
 ,
,
где
 ,
j=1,2,…,
m.
,
j=1,2,…,
m.

Из
приведенных формул видно, что любую
двоичную функцию можно записать,
используя лишь операции ¬,
 ,
,
 .
.
Основная
конъюнкция – это конъюнкция основных
высказываний переменных или их отрицаний.
Например,
 .
.
Основная
дизъюнкция – это дизъюнкция основных
высказываний переменных или их отрицаний.
Например,
 .
.
Конъюнктивной нормальной формой (КНФ) данной формулы называется формула, равносильная данной и представленная в виде конъюнкции основных дизъюнкций. Например, (A+B) (A+C+B) (D+A).
Дизъюнктивной нормальной формой (ДНФ) данной формулы называется формула, равносильная данной и представленная в виде дизъюнкции основных конъюнкций. Например, AB+C+AC.
Теорема 1. Для того чтобы формула алгебры высказываний была тождественно истинной, необходимо и достаточно, чтобы ее КНФ содержала в каждой элементарной дизъюнкции некоторое высказывание и его отрицание.
Теорема 2. Для того чтобы формула алгебры высказываний была тождественно ложной, необходимо и достаточно, чтобы ее ДНФ содержала в каждой элементарной конъюнкции некоторое высказывание и его отрицание.
Совершенные дизъюнктивные, конъюнктивные и полиномиальные нормальные формы представления переключательных (логических) функций. Многообразие формул, посредством которых может быть выражена любая логическая функция, определяет многообразие форм логических функций, т. е. способов их записи путем применения к переменным и их группам элементарных логических операций. Наиболее удобными для практического использования оказываются совершенные нормальные формы представления сложных логических функций. В алгебре логики доказывают, что любая логическая функция F (A, B, C,…, N) может быть представлена только одной совершенной дизъюнктивной нормальной формой (кроме константы нуль) или только одной совершенной конъюнктивной нормальной формой (кроме константы единица).
Пусть функция X=F (A, B, C) задана таблицей 4. Запись функции Х в виде логической суммы (дизъюнкции) логических произведений (конъюнкций) переменных, для которых значение функции Х равно 1, и является совершенной дизъюнктивной нормальной формой (СДНФ) представления логической функции.
Таблица 4
|
A |
B |
C |
X |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
СДНФ логической функции следует находить в такой последовательности:
1) составить произведения переменных для строк таблицы истинности, в которых Х равна 1. Если значение переменной (А, В или С) в строке равно 0, то в произведении записывается отрицание этой переменной;
2) написать сумму произведений, для которых функция Х равна 1. Полученная сумма и является СДНФ. В общем виде
 , (1)
, (1)
Это правило называют правилом записи переключательной функции по единицам. Согласно этому правилу, данные табл. 4 описываются аналитическим выражением, связывающим все наборы переменных, для которых Х=1, в виде:
 . (2)
. (2)
Запись функции Х в виде логического произведения (конъюнкции) логических сумм (дизъюнкций) переменных, для которых функция Х равна 0, является совершенной конъюнктивной нормальной формой (СКНФ) представления логической функции.
Для табл. 4 аналитическое выражение в СДНФ, связывающее все наборы переменных, для которых Х=0, имеет вид:
 . (3)
. (3)
Для представления логической функции Х в СКНФ произведем операцию отрицания левой и правой частей равенства (3)

и на основании законов двойного отрицания и инверсии

 . (4)
. (4)
СКНФ логической функции, согласно (4), следует находить в такой последовательности:
1) составить логические суммы переменных для строк таблицы истинности, в которых функция Х равна 0. Если значение переменной (А, В или С) в строке равно 1, то в сумме записывается отрицание этой переменной;
2) написать логическое произведение составленных логических сумм. Полученное произведение и является СКНФ. В общем виде:
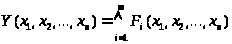 , (5)
, (5)
где F>i> – сложные дизъюнкции.
Это правило также называют правилом построения переключательной функции по нулям.
Кроме представления функций в виде СДНФ и СКНФ используют и совершенную полиномиальную нормальную форму СПНФ. Вместо дизъюнкции может быть записана функция сложения по модулю два (сумма Жегалкина):
 , (6)
, (6)
где F>i> – сложные конъюнкции.
Существует специальная таблица, в которой все элементарные логические операции от двух аргументов представлены в двух совершенных нормальных формах.
Нормальные формы представления переключательной функции иногда называют стандартными (табл. 5).
Таблица 5
|
f |
A 0011 B 0101 |
Название функции |
Обозначение функции |
СДНФ |
СКНФ |
|
f>0> |
0000 |
Константа нуль |
0 |
Не имеет |
|
|
f>1> |
0001 |
Логическое произведение, конъюнкция |
|
|
|
|
f>2> |
0010 |
Функция запрета по В |
|
|
|
|
f>3> |
0011 |
Переменная А |
|
|
|
|
f>4> |
0100 |
Функция запрета по А |
|
|
|
|
f>5> |
0101 |
Переменная В |
|
|
|
|
f>6> |
0110 |
Сумма по мо дулю 2, логическая неравнозначность |
|
|
|
|
f>7> |
0111 |
Логическое сложение, дизъюнкция |
|
|
|
|
f>8> |
1000 |
Операция (стрелка) Пирса, операция Вебба |
|
|
|
|
f>9> |
1001 |
Эквивалентность, логическая равнозначность |
|
|
|
|
f>10> |
1010 |
Инверсия В |
|
|
|
|
f>11> |
1011 |
Импликация от В к А |
|
|
|
|
f>12> |
1100 |
Инверсия А |
|
|
|
|
f>13> |
1101 |
Импликация от А к В |
|
|
|
|
f>14> |
1110 |
Операция (штрих) Шеффера |
|
|
|
|
f>15> |
1111 |
Константа единица |
1 |
|
Не имеет |
Многочленом Жегалкина называется многочлен, являющийся суммой константы 0 или 1 и различных одночленов, в которые все переменные входят не выше, чем в первой степени.
Теорема. Любая функция булевой алгебры может быть представлена, и притом единственным образом, с помощью полинома Жегалкина вида
J
= .
.
Представим,
например, в виде полинома выражение
вида X>1> X>2>.
Для этого проведем следующие рассуждения.
X>2>.
Для этого проведем следующие рассуждения.
Пусть
X>1> X>2
>=
aX>1>X>2>+bX>1>+cX>2>+k,
X>2
>=
aX>1>X>2>+bX>1>+cX>2>+k,
где а, b, с, k – неопределенные коэффициенты.
При X>1> = X>2> = 0 имеем k = 0. При Х>1> = 1, X>2>= 0 имеем b= 1. При Х>1>= 0, Х>2>= 1 имеем с= 1. При X>1>=Х>2>= 1 имеем а + b + с = 1, т. е. а = -1. Таким образом, получаем:
X>1> X>2
>= –
X>1>X>2>+
X>1>+
X>2>.
X>2
>= –
X>1>X>2>+
X>1>+
X>2>.
СПНФ
образуется путем замены в СДНФ:
 на + и
на + и
 на
на
1
 х.
х.
 ,
,
 ,
,

В
последнем случае выражение для
 легко можно упростить, если раскрыть
скобки и взаимно сократить все одинаковые
слагаемые, входящие в формулу четное
число раз:
легко можно упростить, если раскрыть
скобки и взаимно сократить все одинаковые
слагаемые, входящие в формулу четное
число раз:
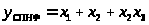 .
.
Подобное упрощение, которое называется минимизацией логической функции, можно осуществить и по отношению к СДНФ и СКНФ.
Таблица 6
|
|
|
|
y |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
Применение
законов алгебры логики позволяет найти
более компактные аналитические выражения
для заданной функции у,
т. е. минимальную дизъюнктивную
нормальную форму
 .
Приведем соответствующие формы
представления функции у,
заданной табл. 6:
.
Приведем соответствующие формы
представления функции у,
заданной табл. 6:
 ,
,
и для СКНФ, т. е. минимальную КНФ:
 .
.
После
того, как найдены минимальные нормальные
формы (МНФ), их рекомендуется проверить
на всех наборах аргументов
 .
Переменные
.
Переменные
 или
или
 часто называют термами. Именно полный
набор из n
термов образует конституенту. В процессе
же минимизации некоторые термы из
конституент пропадут. Тогда оставшуюся
часть дизъюнкта или конъюнкта называют
импликантой.
часто называют термами. Именно полный
набор из n
термов образует конституенту. В процессе
же минимизации некоторые термы из
конституент пропадут. Тогда оставшуюся
часть дизъюнкта или конъюнкта называют
импликантой.
Как мы только что убедились на примере, импликанты появляются в результате склейки смежных конституент, различающихся одним термом.
Контрольные вопросы и упражнения
1. Дайте определение логической функции многих переменных.
2. Что такое вектор значений булевой функции? Приведите пример построения таблицы истинности логической функции многих переменных.
3. Сколько существует булевых функций от n переменных?
4. Что такое ДНФ и КНФ?
5. Каков алгоритм построения СДНФ? Приведите пример построения СДНФ.
6. Каков алгоритм построения СКНФ? Приведите пример построения СКНФ.
7.
Составьте СКНФ и СДНФ для функции
 .
.
8. Приведите пример построения СПНФ.
3.7 Некоторые замкнутые классы (классы Поста). Понятие базиса
Система булевых функций {f>1>, f>2>,…, f>m>} называется полной, если любая булева функция может быть выражена через функции f>1>, f>2>,…, f>m> с помощью суперпозиций.
Пусть К0={f>1>(x>1,…,>x>k>>1>), f>2>(x>1,…,>x>k>>2>),…, f>m>(x>1,…,>x>km>)} – конечная система булевых функций. Функция f называется элементарной суперпозицией (суперпозицией ранга 1) функций f>1>, f>2>,…, f>m>>,> если f может быть получена одним из следующих способов:
а) переименованием некоторой переменной x>j> какой-нибудь функции f>i>;
б)
подстановкой некоторой функции
 вместо какой-либо переменной x>j>
любой из функций
вместо какой-либо переменной x>j>
любой из функций
 .
.
Суперпозиции ранга 1 образуют класс функций К1. Класс функций, получающийся из функций класса Ks-1 суперпозицией ранга s 1 с помощью элементарных суперпозиций, называется классом функций Ks суперпозиций ранга s. Суперпозициями функций из К0 называются функции, входящие в какой-то из классов Ks.
Согласно введенным определениям, можно говорить, что система булевых функций полна. Тогда любую булеву функцию можно представить в виде многочлена от своих переменных.
В
современном компьютере цифрами являются
ноль и единица. Следовательно, команды,
которые выполняет процессор, суть булевы
функции. Мы уже видели, что любая булева
функция реализуется через конъюнкцию,
дизъюнкцию и отрицание. Следовательно,
можно построить нужный процессор, имея
в распоряжении элементы, реализующие
 .
Далее рассмотрим вопрос: существуют ли
(и если существуют, то какие) другие
системы булевых функций, обладающие
тем свойством, что с их помощью можно
выразить все другие функции. Рассмотрим
некоторые замкнутые классы (классы
Поста), их пять.
.
Далее рассмотрим вопрос: существуют ли
(и если существуют, то какие) другие
системы булевых функций, обладающие
тем свойством, что с их помощью можно
выразить все другие функции. Рассмотрим
некоторые замкнутые классы (классы
Поста), их пять.
1. Класс функций, сохраняющих константу нуль (обозначается T>0 >или P>0>):
T>0>:={f | f (0,0,…, 0)=0}.
К
этому классу относятся, например, функции
 ;
;
 ;
;
 ;
;
 .
.
2. Класс функций, сохраняющих константу единица (обозначается T>1 >или P>1>):
T>1>:={f | f (1,1,…, 1)=1}.
К нему относятся все нечетные функции.
3. Класс самодвойственных функций (обозначается T>* >или S):
T>*>:={f | f*};

Пример
 и
и
 .
.
Функция
 называется двойственной по отношению
к функции
называется двойственной по отношению
к функции
 ,
если
,
если
 .
Двойственная функция получается из
исходной при замене значений всех
переменных, а также значений функции
на противоположные, т. е. в таблице
истинности нужно заменить 0 на 1, 1 на 0.
.
Двойственная функция получается из
исходной при замене значений всех
переменных, а также значений функции
на противоположные, т. е. в таблице
истинности нужно заменить 0 на 1, 1 на 0.
Пример.
Двойственной к функции
 является функция, соответствующая
формуле
является функция, соответствующая
формуле
 ,
т. е.
,
т. е.
 или
или
 :
:
 .
Аналогично
.
Аналогично
 ,
,
 .
.
Принцип двойственности:
Если
 ,
,
то
 .
.
Таким образом, функция, двойственная суперпозиции функций, есть соответствующая суперпозиция двойственных функций.
Этот принцип удобен при нахождении двойственных функций, представленных формулами, содержащими лишь конъюнкции, дизъюнкции и отрицание. В этом случае в исходной формуле конъюнкции заменяются на дизъюнкции, а дизъюнкции – на конъюнкции. Таким образом, ДНФ соответствует КНФ, КНФ – ДНФ, СДНФ – СКНФ, СКНФ – СДНФ.
Пример.
 ,
,
если
 ,
то и
,
то и
 .
.
Функция
 называется самодвойственной, если
называется самодвойственной, если
 .
.
Пример.
Покажем, что формула
 задает самодвойственную функцию.
задает самодвойственную функцию.
Убедимся,
что на всех противоположных наборах
значений переменных
 и
и
 формула принимает противоположные
значения. Действительно, составим
таблицу истинности:
формула принимает противоположные
значения. Действительно, составим
таблицу истинности:
|
|
x |
y |
z |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
Получаем
 ,
,
 ,
,
 ,
,
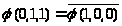 .
.
4. Класс монотонных функций (обозначается T>M>> >или M):
 ,
где
,
где
 ,
,
 ,
,
 ,
,
 .
.
5. Класс линейных функций (обозначается T>L>> >или L):
 .
.
Эквивалентность
является линейной функцией
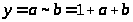 .
Стрелка Пирса – нет,
.
Стрелка Пирса – нет,
 .
.
 ,
,
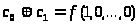 ,
,
 ,…,
,…,
 ,
,
т. е.
 ,
,
 ,…,
,…,
 . (7)
. (7)
Таким
образом, проверка линейности сводится
к нахождению коэффициентов
 по формулам (7) и сопоставлению таблиц
истинности данной формулы
по формулам (7) и сопоставлению таблиц
истинности данной формулы
 и полученной формулы
и полученной формулы
 .
.
Пример.
Проверим, является ли линейной функция
 .
Имеем
.
Имеем
 ,
,
 ,
,
 .
Таким образом,
.
Таким образом,
 .
Сопоставляя таблицы истинности формул
.
Сопоставляя таблицы истинности формул
 и
и
 ,
убеждаемся, что они не совпадают. Вывод:
функция
,
убеждаемся, что они не совпадают. Вывод:
функция
 нелинейна.
нелинейна.
Линейность функции можно также определить с помощью следующей теоремы.
Теорема
Жегалкина. Всякая булева функция
 представима полиномом Жегалкина, т. е.
в виде
представима полиномом Жегалкина, т. е.
в виде
 ,
где в каждом наборе (i>1>,…,
i>k>)
все i>j>
различны, а суммирование ведется по
некоторому множеству таких несовпадающих
наборов. Представление булевой функции
в виде полинома Жегалкина единственно
с точностью до порядка слагаемых.
,
где в каждом наборе (i>1>,…,
i>k>)
все i>j>
различны, а суммирование ведется по
некоторому множеству таких несовпадающих
наборов. Представление булевой функции
в виде полинома Жегалкина единственно
с точностью до порядка слагаемых.
Полином Жегалкина называется нелинейным (линейным), если он (не) содержит произведения переменных.
Таким образом, линейность булевой функции равносильна линейности соответствующего полинома Жегалкина.
Для
получения полинома Жегалкина булевой
функции, находящейся в СДНФ, используются
аксиомы булевой алгебры, аксиомы булева
кольца
 и равенства, выражающие операции
и равенства, выражающие операции
 через операции этого булева кольца:
через операции этого булева кольца:
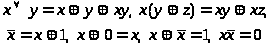 и т. д.
и т. д.
Пример.
Определим линейность функции
 .
.
Имеем

Полученный полином Жегалкина является нелинейным, и, следовательно, функция f также нелинейна.
Заметим,
что если в эквивалентности
 формулы
формулы
 являются различными конституентами
единицы, то их произведение
являются различными конституентами
единицы, то их произведение
 равно 0, и тогда
равно 0, и тогда
 .
Следовательно, для получения полинома
Жегалкина из СДНФ можно сразу заменить
.
Следовательно, для получения полинома
Жегалкина из СДНФ можно сразу заменить
 .
.
Отметим, что каждый класс Поста замкнут относительно операций замены переменных и суперпозиции, т. е. с помощью этих операций из функций, принадлежащих данному классу, можно получить только функции из этого же класса.
Пример.
Определим, к каким классам Поста относится
булева функция
 .
.
Так
как f
(0,0)=1, а f
(1,1)=0, то
 и
и
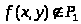 .
Поскольку
.
Поскольку
 ,
то
,
то
 .
Так как f
(0,0)>f
(1,1), то
.
Так как f
(0,0)>f
(1,1), то
 .
Полином Жегалкина для функции
.
Полином Жегалкина для функции
 имеет вид
имеет вид
 в силу равенства
в силу равенства
 .
Поэтому данная функция нелинейна. Таким
образом, можно составить следующую
таблицу
.
Поэтому данная функция нелинейна. Таким
образом, можно составить следующую
таблицу
Таблица функций
|
Функция |
Классы |
||||
|
Р>0> |
Р>1> |
S |
М |
L |
|
|
х | у |
Нет |
Нет |
Нет |
Нет |
Нет |
Теорема Поста. Система F булевых функций тогда и только тогда является полной, когда для каждого из классов P>0>, P>1>, S, M, L в системе F найдется функция, не принадлежащая этому классу.
В
силу теоремы Поста функция х
| у
образует полную систему, т. е. с помощью
штриха Шеффера можно получить любую
булеву функцию. В частности,
 .
.
Система булевых функций называется базисом, если она полна, а удаление любой функции из этой системы делает ее неполной.
Теорема. Каждый базис содержит, не более четырех булевых функций.
Доказательство.
Предположим, что существует базис F,
состоящий более чем из четырех функций.
По теореме Поста тогда получаем, что F
состоит ровно из пяти функций, каждая
из которых не принадлежит ровно одному
классу Поста. Пусть f
– функция из F,
не принадлежащая классу Р>0>.
Тогда, с одной стороны, f
(0,0,…, 0)=1,
а, с другой – из
 следует, что f
(1,1,…, 1)=1.
Это означает, что f
не является самодвойственной функцией,
что противоречит предположению.
следует, что f
(1,1,…, 1)=1.
Это означает, что f
не является самодвойственной функцией,
что противоречит предположению.
Пример.
Следующие системы булевых функций
являются базисами:
 .
.
Таблица 7
|
Обоснование |
Базис |
|
следовательно,
|
{И, НЕ} – конъюнктивный базис |
|
следовательно,
|
{ИЛИ, НЕ} – дизъюнктивный базис |
|
|
{И,
|
|
следовательно,
|
{|} – базис Шеффера |
|
следовательно,
|
{ |
Пример.
Конъюнкции,
то есть все функции вида
 ,
тоже составляют замкнутый класс.
Очевидно, однако, что, например, функцию,
которая на наборе (0,0,…, 0) имеет значение
1, нельзя представить суперпозицией
таких функций. Таким образом, {И} не
является базисом, следовательно,
конъюнктивный базис {И, НЕ} является
минимальным.
,
тоже составляют замкнутый класс.
Очевидно, однако, что, например, функцию,
которая на наборе (0,0,…, 0) имеет значение
1, нельзя представить суперпозицией
таких функций. Таким образом, {И} не
является базисом, следовательно,
конъюнктивный базис {И, НЕ} является
минимальным.
Рассмотрим более подробно базис Жегалкина.
Алгебра Жегалкина и линейные функции
Алгебра
Жегалкина – это алгебра над множеством
двух бинарных булевых функций (И,
 )
и нульарной функции 1. Легко проверить
следующие соотношения в этой алгебре:
)
и нульарной функции 1. Легко проверить
следующие соотношения в этой алгебре:
 ;
;
 ;
;
 ;
;
 .
.
Если в произвольной формуле, включающей только функции базиса Жегалкина, раскрыть скобки, то получим бесскобочную формулу, имеющую вид суммы (по модулю два) произведений, то есть некоторый полином. Он называется полиномом Жегалкина.
Широкий набор базисов открывает большие возможности при решении задач минимизации схем устройств дискретного действия, поскольку из базисных схем с помощью суперпозиций можно составить схему, соответствующую любой булевой функции.
Контрольные вопросы и упражнения
1. Дайте определение полной системе булевых функций.
2. Перечислите классы Поста.
3. Дайте определение двойственной функции. Приведите примеры.
4. Дайте определение самодвойственной функции. Приведите примеры.
5. Постройте полином Жегалкина для функции «стрелка Пирса».
6. Сформулируйте теорему Поста.
7. Что такое базис? Приведите примеры базисов.
3.8 Методы минимизации логических функций
Наиболее употребляемая операция при минимизации функций – это операция склеивания.
AB+ ĀB=B (A+ Ā)=B.
Рассмотрим три наиболее распространенных метода минимизации.
1. Пусть будут заданы номера наборов четырех переменных, на которых логическая функция принимает единичное значение: f (2,5,6,7,10,12,13,14)=1.
Выразим эту логическую функцию в СДНФ (символ конъюнкции писать не будем):
f (0010,0101, 0110, 0111, 1010, 1100, 1101, 1110) =
 .
.
На первом этапе минимизации исходную СДНФ можно упростить за счет использования закона склеивания, тогда получим:
 .
.
Обращаем внимание на то, что одну и ту же конституенту (импликанту) можно склеивать с другими конституентами (импликантами) многократно, так как в логике Буля действует закон идемпотентности:
 ,
,
поэтому любую конституенту можно размножить.
На втором этапе воспользуемся таблицей Куайна (табл. 8), в соответствии с которой данный метод минимизации получил свое наименование – метод Куайна. В таблице по вертикали перечислены все полученные на первом этапе упрощения импликанты, а по горизонтали – исходные конституенты. Единица в табл. 8 стоит там, где импликанта «накрывает» конституенту. Дело в том, что конституента всегда может быть заменена импликантой или даже отдельным термом по закону поглощения:

Таблица 8
|
|
0010 |
0101 |
0110 |
0111 |
1010 |
1100 |
1101 |
1110 |
|
– – 1 0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
0 1 – 1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 1 1 – |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
– 1 0 1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 1 0 – |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
1 1 – 0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
После заполнения таблицы Куайна у нас получилось так, что почти в каждой графе оказалось по две единицы; между тем достаточно иметь одну единицу в графе. Поэтому, по возможности, нужно исключить избыточные единицы. Выбор единиц производится из соображений минимальности числа термов (выбранные единицы затемнены). В итоге оказалось, что можно обойтись только тремя импликантами вместо шести:
 .
.
С помощью таблиц истинности легко проверить, что полученная в МНФ функция воспроизводит все значения исходной функции. Отметим, что в общем случае решений по критерию минимума термов может быть несколько.
2.
Не менее эффективным способом минимизации
логических функций является метод
сочетания индексов. Для его изложения
составим табл. 9, в графах которой записаны
возможные сочетания индексов. В последней
графе выписаны значения функции. Анализ
таблицы начинается слева по столбцам.
Принцип исключения i,
j кода
следующий. На пересечении i столбца,
например, с сочетанием индексов 23, и
j строки,
например, 3 ей, находится код 10, что
соответствует импликанте
 .
Следовательно, в этом столбце везде,
где встречается код 10, т. е. в строках
2, 3, 10 и 11, эти коды исключаются, поскольку
значение функции в 3 ей строке равно
нулю. Теперь возьмем столбец с сочетанием
индексов 124. Здесь во 2 ой и 6 ой
строках оставлены коды 010, а в 10 ой и
14 ой строках – код 011. Сделано это
потому, что эти коды встречаются только
на строках со значением функции, равным
единице. Напротив, код 110 этого же столбца
встречается как при единичных значениях
функции, так и при нулевых.
.
Следовательно, в этом столбце везде,
где встречается код 10, т. е. в строках
2, 3, 10 и 11, эти коды исключаются, поскольку
значение функции в 3 ей строке равно
нулю. Теперь возьмем столбец с сочетанием
индексов 124. Здесь во 2 ой и 6 ой
строках оставлены коды 010, а в 10 ой и
14 ой строках – код 011. Сделано это
потому, что эти коды встречаются только
на строках со значением функции, равным
единице. Напротив, код 110 этого же столбца
встречается как при единичных значениях
функции, так и при нулевых.
Таблица 9
|
n |
1 |
2 |
3 |
4 |
12 |
13 |
14 |
23 |
24 |
34 |
123 |
124 |
134 |
234 |
1234 |
y |
|
0 |
0 |
0 |
0 |
0 |
00 |
00 |
00 |
00 |
00 |
00 |
000 |
000 |
000 |
000 |
0000 |
0 |
|
1 |
1 |
0 |
0 |
0 |
10 |
10 |
10 |
00 |
00 |
00 |
100 |
100 |
100 |
000 |
1000 |
0 |
|
2 |
0 |
1 |
0 |
0 |
01 |
00 |
00 |
10 |
10 |
00 |
010 |
010 |
000 |
100 |
0100 |
1 |
|
3 |
1 |
1 |
0 |
0 |
11 |
10 |
10 |
10 |
10 |
00 |
110 |
110 |
100 |
100 |
1100 |
0 |
|
4 |
0 |
0 |
1 |
0 |
00 |
01 |
00 |
01 |
00 |
10 |
001 |
000 |
010 |
010 |
0010 |
0 |
|
5 |
1 |
0 |
1 |
0 |
10 |
11 |
10 |
01 |
00 |
10 |
101 |
100 |
110 |
010 |
1010 |
1 |
|
6 |
0 |
1 |
1 |
0 |
01 |
01 |
00 |
11 |
10 |
10 |
011 |
010 |
010 |
110 |
0110 |
1 |
|
7 |
1 |
1 |
1 |
0 |
11 |
11 |
10 |
11 |
10 |
10 |
111 |
110 |
110 |
110 |
1110 |
1 |
|
8 |
0 |
0 |
0 |
1 |
00 |
00 |
01 |
00 |
01 |
01 |
000 |
001 |
001 |
001 |
0001 |
0 |
|
9 |
1 |
0 |
0 |
1 |
10 |
10 |
11 |
00 |
01 |
01 |
100 |
101 |
101 |
001 |
1001 |
0 |
|
10 |
0 |
1 |
0 |
1 |
01 |
00 |
01 |
10 |
11 |
01 |
010 |
011 |
001 |
101 |
0101 |
1 |
|
11 |
1 |
1 |
0 |
1 |
11 |
10 |
11 |
10 |
11 |
01 |
110 |
111 |
101 |
101 |
1101 |
0 |
|
12 |
0 |
0 |
1 |
1 |
00 |
01 |
01 |
01 |
01 |
11 |
001 |
001 |
011 |
011 |
0011 |
1 |
|
13 |
1 |
0 |
1 |
1 |
10 |
11 |
11 |
01 |
01 |
11 |
101 |
101 |
111 |
011 |
1011 |
1 |
|
14 |
0 |
1 |
1 |
1 |
01 |
01 |
01 |
11 |
11 |
11 |
011 |
011 |
011 |
111 |
0111 |
1 |
|
15 |
1 |
1 |
1 |
1 |
11 |
11 |
11 |
11 |
11 |
11 |
111 |
111 |
111 |
111 |
1111 |
0 |
Итак, все коды на строках, заканчивающихся нулевыми значениями функции, исключаются автоматически. Если эти коды попадают на строки, заканчивающиеся единичным значением функции, то они также не учитываются. Остаются только те коды, которые расположены на строках с единичным значением функции (эти коды затемнены).
Далее
руководствуются следующим правилом.
Для того чтобы функция приняла значение,
равное единице, достаточно того, чтобы
только какая-нибудь одна импликанта на
строке приняла единичное значение.
Прежде всего, оставляем минимальную
импликанту
 ,
которая перекрывает единицы в строках
2, 6, 10 и 14. Затем, естественно, обращаемся
к 12 ой строке. Здесь оставляем
единственный на строке код 011, что
отвечает импликанте
,
которая перекрывает единицы в строках
2, 6, 10 и 14. Затем, естественно, обращаемся
к 12 ой строке. Здесь оставляем
единственный на строке код 011, что
отвечает импликанте
 .
Эта же импликанта ответственна за 13 ую
строку, оканчивающуюся тоже единицей.
Осталось рассмотреть 5 ую и 7 ую
строки. Общей для них является импликанта:
.
Эта же импликанта ответственна за 13 ую
строку, оканчивающуюся тоже единицей.
Осталось рассмотреть 5 ую и 7 ую
строки. Общей для них является импликанта:
 .
Таким образом, тремя импликантами мы
перекрыли все единичные значения
функции, что совпадает с результатом,
полученным на основе таблиц Куайна.
.
Таким образом, тремя импликантами мы
перекрыли все единичные значения
функции, что совпадает с результатом,
полученным на основе таблиц Куайна.
3. Существует графический способ склеивания, который получил название метод карты Карно (представлен в табл. 10). Выделяем смежные единицы, это и будут слагаемые нашей функции.
Таблица 10
|
x>3>x>4> x>1>x>2> |
00 |
01 |
11 |
10 |
|
00 |
0 |
0 |
1 |
1 |
|
01 |
1 |
0 |
0 |
0 |
|
11 |
1 |
0 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
 – получили два слагаемых
– получили два слагаемых
Хотя табл. 9 более громоздка, чем табл. 8, метод сочетания индексов не считается более сложным, чем метод Куайна, если помнить, что до составления таблиц Куайна необходимо произвести многочисленные склейки конституент и импликант. Реализация на компьютере алгоритма метода сочетания индексов оказывается сравнительно простой. И напротив, внешняя простота и наглядность третьего метода минимизации логических функций с помощью карт Карно оборачивается сложной программой при реализации алгоритма на компьютере.
Таблица 11
|
|
|
|
|
||
|
|
1100 |
1110 |
0110 |
0100 |
|
|
|
1101 |
1111 |
0111 |
0101 |
|
|
|
1001 |
1011 |
0011 |
0001 |
|
|
|
1000 |
1010 |
0010 |
0000 |
|
|
|
|
|
|
Таблица 12



Карта Карно для четырех переменных представлена в виде табл. 11. Каждая клетка карты соответствует конституенте. Заполненная карта представлена табл. 12 (функция взята та же, что и в первых двух методах). Согласно закону склеивания, две смежные конституенты с единичными значениями всегда можно объединить для получения соответствующей импликанты. Причем смежными считаются и те, которые лежат на границах карты. Какие именно единицы требуется объединить для получения подходящей импликанты, легко определить визуально. Следует также помнить, что в соответствии с законом идемпотентности одна и та же единица табл. 12 может склеиваться с двумя или тремя смежными единицами.
Контрольные вопросы
1. Перечислите основные методы минимизации функций.
2. Расскажите о методе Куайна.
3. Расскажите о методе карт Карно.
3.9 Неполностью определенные логические функции
Ранее мы рассматривали ситуации, когда на множество аргументов или логических переменных x>1>, x>2>,…, x>n> не накладывались ограничения, или, что то же самое, функции были определены на всем наборе аргументов. Однако реально на практике функции либо не определены полностью, либо есть запрещенные комбинации. Необходимо доопределить функцию таким образом, чтобы аналитическая форма ее представления была минимальной, далее производят склейки (пример приведён в табл. 13).
Таблица 13
|
x>3>x>4> x>1>x>2> |
00 |
01 |
11 |
10 |
|
00 |
0* |
0 |
1* |
0 |
|
01 |
1* |
1 |
1 |
1* |
|
11 |
0 |
0 |
1 |
0* |
|
10 |
0* |
0* |
1* |
0* |
 .
.
* – эти значения доопределили сами, исходя того, чтобы выражение для функции F было минимальным.
3.10 Формы представления булевых функций
К настоящему времени мы знакомы с двумя формами представления булевых функций: таблица истинности и формула (аналитическая запись). Рассмотрим еще две формы представления таких функций.
3.10.1 Семантические деревья
Семантическое дерево – это двоичное дерево, корень которого помечен двоичной функцией от m переменных, из каждого узла идут по два ребра, соответствующих двум значениям очередной переменной, а 2m листьев помечены соответствующими значениями функции.
3.10.2 Бинарные диаграммы решений (БДР)
Бинарная диаграмма решений (Binary Decision Diagrams, BDD) – это граф, являющийся модификацией семантического дерева. В БДР узлы с одним и тем же значением функции объединены. Если на каждом уровне БДР все вершины имеют одну и ту же метку (одинаковые переменные), то такая БДР называется упорядоченной (в англоязычной литературе такое представление называется Ordinary Binary Decision Diagrams, или сокращенно OBDD). Будем называть такое представление УБДР. Вершины УБДР расположены по уровням, каждому уровню соответствует одна переменная, которая помечает вершины, находящиеся на этом уровне. Из каждой вершины выходят два ребра: одно соответствует нулевому значению соответствующей переменной (будем его изображать штриховой линией), а другое – единичному значению этой переменной (оно изображается сплошной линией).
На
рис. 4 показаны все четыре формы
представления функции
 .
.
Бинарные диаграммы решений используются как компактная форма представления булевой функции. Такое представление полезно во многих случаях, например, когда нужно многократно вычислять значения функции при различных наборах значений ее аргументов. Для того чтобы получить значение функции f, например, на языке С, вместо хранения громоздкой таблицы истинности можно вычислить оператор: f=q? (r? 0:1): (р? 0:1), который построен на основании БДР (см. рис. 4). В этом примере использование УБДР позволяет вычислить значение булевой функции, выполнив всего две операции, в то время как при ее вычислении по аналитическому представлению требуется не менее 5 операций.
Рис. 4. Четыре формы представления двоичной функции
|
f (p, q, r) |
Таблица истинности |
Семантическое дерево |
Бинарная диаграмма решений |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Сложность представления функции с помощью УБДР существенно зависит от порядка переменных. Так, например, УБДР для иного порядка переменных, чем на рис. 4, содержит четыре вершины, а не три (рис. 5). Интересной проблемой теоретической информатики является нахождение алгоритма, дающего оптимальный порядок переменных булевой функции с точки зрения представления этой функции упорядоченной БДР.

Рис. 5.
УБДР для функции
 с порядком переменных [p,
q,
r]
с порядком переменных [p,
q,
r]
3.11 Построение логических схем
При синтезе логических схем применяют элементы с одним и несколькими входами. Условия функционирования таких элементов определяются переключательными функциями одной или нескольких переменных.
Входные и выходные сигналы логических схем зависят от времени (одни из них в некоторый момент времени равны 1, в другие моменты времени 0). Логические функции, описывающие работу таких схем, называют переменными. Используют также схемы, для которых во все моменты времени сигналы равны либо 1, либо 0. Логические функции, описывающие работу этих схем, называют постоянными.
Существует только четыре различные переключательные функции одной переменной. Как видно из таблицы 14, только две функции не зависят от переменной А (в этих случаях переменная А фиктивна).
Таблица 14
|
Х |
А |
Условное обозначение |
Название функции |
|
0 1 |
|||
|
X>0>=f>0> (A) X>1>=f>1> (A) X>2>=f>2> (A) X>3>=f>3> (A) |
0 0 0 1 1 0 1 1 |
0 A
1 |
Константа 0 Переменная А Инверсия А Константа 1 |
Для функции двух переменных существует шестнадцать различных переключательных функций. Как видно из таблицы 5, только десять функций существенно зависят от переменных А и В.
На рис. 6, 7 приведены обозначения элементов, реализующих некоторые переключательные функции двух переменных.
Каждой элементарной логической операции можно поставить в соответствие элементарную логическую схему или вентиль. На входе и выходе вентиля мы имеем логические сигналы двух видов, что можно ассоциировать с логическим 0 или логической 1.
1. Элемент «И» 2. Элемент «ИЛИ» 3. Элемент «НЕ»

F=x>1>∙x>2>
F=x>1 >x>2>
F=
>x>2>
F=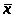
Рис. 6. Символическое обозначение вентилей
а) б) в)

г

 )
д)
е)
)
д)
е)

Рис. 7. Условные обозначения переключательных функций двух переменных: а – элемент Шеффера; б – элемент Пирса; в-импликатор; г – запрет; д – равнозначность; е – сложение по модулю 2
В технической литературе используются обозначения элементов, несколько отличающихся друг от друга.
Логическая схема, которая полностью описывается булевыми выражениями или таблицами истинности, называется комбинационной схемой.
Таким образом, комбинационная схема – схема, в которой значения входных переменных в текущий момент времени полностью определяют значения выходных переменных.
Другой класс схем – последовательностные схемы. Это схемы с внутренней памятью. В них значения выходных переменных определяются не только значениями входных переменных в текущий момент времени, но и их значениями в предыдущие моменты времени.
Будем рассматривать только комбинационные схемы.
До сих пор мы рассматривали поведение логической схемы, таблицы истинности и булевы выражения, использованные для описания значений выходной переменной в зависимости от набора значений входных переменных. Но булево выражение содержит сведения и о структуре логической схемы.
Соединив логические элементы в соответствии с булевыми выражениями, получим логическую схему, реализующую данное выражение.
Логическая связь выхода и входов этой схемы описывается исходным булевым выражением. Таким образом, булево изображение – описание логической схемы.
Контрольные вопросы
1. Перечислите все известные формы представления булевых функций.
2. Перечислите основные элементы, используемые при построении логических схем.
3.12 Логические конечные автоматы
3.12.1 Процессы
Описывая конкретные алгоритмы, мы отмечали, что вычисление по алгоритму можно рассматривать как некоторый процесс, который описывается множеством состояний, начальным состоянием и правилами перехода из состояния в состояние.
Рассмотрим три варианта таких правил и соответственно три в принципе различных процесса:
процесс, в котором переходы выполняются под влиянием некоторых внешних воздействий. Этот процесс называется автоматом;
процесс, в котором переходы выполняются под влиянием некоторого случайного механизма. Таких процессов можно придумать много, простейший из них, который будем рассматривать в дальнейшем, называется марковской цепью;
процесс, в котором переходы выполняются по выбору некоего «одушевленного существа», стремящегося выбрать такой набор или последовательность решений, которые обеспечат ему максимальное значение некоторой функции от траектории процесса. Это управляемые процессы.
Разумеется, кроме таких чистых схем имеются и всякого рода смеси. Однако, чистые схемы интересны тем, что по ним можно увидеть, на что в соответствующей конкретной науке обращается особое внимание, и как сильно традиции этой конкретной науки влияют на изучение одного и того же математического объекта.
3.12.2 Конечные автоматы
Пусть заданы:
М – конечное непустое множество, элементы которого называются состояниями автомата;
А – конечное непустое множество внешних воздействий на автомат (входной алфавит автомата);
В-множество ответов автомата на внешние воздействия (выходной алфавит).
Автомат – это процесс, который рассматривается в дискретные моменты времени (такты работы) и в каждый момент времени получает внешние воздействия. В зависимости от воздействия и текущего состояния процесса переходит в новое состояние и вырабатывает свой ответ.
По сравнению со схемой из функциональных элементов конечный автомат является более точной моделью дискретного преобразователя информации, однако, как и любая модель, понятие конечного автомата связано с рядом упрощающих предположений.
Во-первых, предполагается, что вход (выход) автомата в каждый момент времени может находиться в одном из конечного числа различных состояний. Но у реального преобразователя входной сигнал x(t) представляет собой непрерывную величину, и для описания такого преобразователя с помощью модели конечного автомата нужно разделить диапазон изменения x(t) на конечное число уровней и произвести квантование.
Во-вторых, предполагается, что время изменяется дискретно. Это означает, что состояния входа и выхода устройства отмечаются только в определенные моменты времени, образующие дискретную последовательность
t>1>, t>2>,…, t>n>. Каждый момент времени однозначно определяется его индексом, поэтому с целью упрощения будем считать, что время t принимает значения 1, 2, 3,…, n. Промежуток (n, n+1) называется тактом.
Конечный автомат является математической моделью реальных дискретных устройств по переработке информации. Структура теории конечных автоматов определяется теми задачами, которые возникают при производстве и эксплуатации таких устройств.
Теория автоматов – раздел теоретической кибернетики, в котором изучаются математические модели (называемые автоматами, машинами) реально существующих (механических, биологических и т. п.) или принципиально возможных устройств, перерабатывающих дискретную информацию дискретными временными тактами.
Теория автоматов возникла, главным образом, под влиянием запросов техники цифровых вычислительных и управляющих машин, а также внутренней потребности теории алгоритмов и математической логики.
Понятие «автомата» заметно варьируется в зависимости от характера названных устройств, от принятого уровня абстракции и целесообразной степени общности (автоматы конечные, бесконечные, растущие, вероятностные, детерминированные, автономные и т. п.).
Автомат можно рассматривать как частный случай общего понятия управляющей системы. В теории автоматов широко применяется аппарат алгебры, математической логики, комбинаторного анализа (включая теорию графов) и теорию вероятностей.
Конечные и бесконечные автоматы характеризуются соответственно конечностью и бесконечностью объема памяти (число внутренних состояний). Конечными автоматами являются отдельные блоки компьютера и даже компьютер в целом. Мозг тоже можно также рассматривать как конечный автомат. Бесконечные автоматы представляют собой естественную математическую идеализацию, вырастающую из представления об автомате с конечным, но необратимо большим числом состояний.
Анализ автоматов – нахождение по заданному в том или ином виде автомату отображения «вход-выход», осуществляемого этим автоматом; часто такое отображение можно интерпретировать как вычисление предиката, и поскольку каждый предикат характеризуется своим множеством истинности, то задача анализа автомата сводится к нахождению этого множества (говорят, что это множество распознается автоматом).
Для многих классов автоматов хорошо известны классы распознаваемых ими множеств. Например, машины Тьюринга распознают все рекурсивно перечислимые множества, автоматы с магазинной памятью (недетерминированные) – контекстно свободные языки.
Далеко не всегда по заданным автомату и множеству удается определить, распознает ли автомат в точности это множество. В общем виде для произвольного класса автоматов или даже для произвольного конкретного автомата эта проблема является алгоритмически неразрешимой. Если наложить ограничения на способы задания автоматов и на способы задания множеств, то для многих случаев она становится разрешимой. Например, если регулярные события задавать регулярными выражениями, а конечные автоматы – матрицами переходов и выходов, то существует общий конструктивный прием (алгоритм анализа конечных автоматов), позволяющий находить регулярные выражения для событий, представляемых в произвольном конечном автомате.
Синтез автоматов – построение автоматов по заданному поведению «вход-выход». Проблема синтеза наиболее подробно исследовалась для конечных автоматов, поскольку к этому случаю сводятся многие практические задачи, связанные с проектированием разного рода управляющих и вычислительных устройств.
Трудности синтеза автоматов зависят в основном от того, как заданы условия функционирования автомата. Чем выразительнее язык, применяемый для задания условий функционирования аппарата (т. е., чем удобнее он для заказчика), тем сложнее метод синтеза. Во многих случаях может оказаться, что единого метода синтеза не существует. Поэтому для ряда классов автоматов, в частности, для конечных автоматов, разрабатываются специальные языки, с помощью которых удобно задавать условия функционирования автоматов, для которых существуют методы синтеза (регулярные события и выражения, логический язык для задания автоматов).
Минимизация числа состояний автомата – по произвольному заданному конечному автомату создается автомат с наименьшим возможным числом состояний, обладающий тем же поведением, что и исходный автомат. Решение этой задачи состоит в нахождении эффективного алгоритма минимизации. Оно представляет интерес, как в абстрактной теории автоматов, так и в проектировании реальных автоматов.
Рассмотрим модели, которые представлены в виде некоторого черного ящика, на вход которого поступают некоторые логические переменные x>1>, x>2>,…, x>n>. Объект их перерабатывает, и на выходе получаем некоторые логические функции y>1>, y>2>,…, y>k>.
x>1>
x>2>
.
x>n>
y>1>
y>2>
.
y>k>
Объект

Входные
переменные
Выходные
функции




Рис. 8. Логический конечный автомат
Такие модели называют логически конечными автоматами. Существуют некоторые классы таких автоматов:
автоматы без памяти (комбинационные)
автоматы с памятью (последовательностные).
3.12.2.1 Конечные автоматы без памяти (комбинационные)
Общая формула, описывающая этот вид автоматов:
 ,
i
= 1, 2, …, k.
,
i
= 1, 2, …, k.
 – в векторной форме
– в векторной форме
Пример 1.
Примером таких автоматов является простая экспертная система профессиональной пригодности, где входные значения – это ответы на n вопросов, а выходные – k выводов о том, может ли человек работать в данной области.
Пример 2.
Диагностика неисправностей, заболеваний и т. д.
Пример 3.
Пусть функционирование логического автомата описывается формулой:
 .
.
На языке Pascal оператор присваивания, соответствующий этой формуле:

Для более сложной модели получается структура типа запись:
Type
Prep = record
Number: Integer;
Stroka: String;
Zn: Boolean;
End;
Далее моделируется базис, который будет работать с этими высказываниями. Для каждой логической операции пишем процедуру или функцию.
Function otr (a: prep; var b: prep; параметры сохранения и т. д.): Boolean;
Function con (a, b: prep; var c: prep; параметры сохранения и т. д.): Boolean;
Function diz (a, b: prep; var c: prep; параметры сохранения и т. д.): Boolean;
Пример 4.
Отмоделировать функцию Y>i>:

Высказывание моделируется записью:
Function y1 (x>1>, x>2>, x>3>, x>4:> prep; var rez: prep; sohr: Boolean; newnumber: Integer; t: String): Boolean;
Var
I: boolean; a, b, c, d, e,: prep;
Begin
I:= otr(x>1>, a, false, 0);
I:= otr(x>2>, b, false, 0);
I:= con (a, b, c, false, 0);
I:= con (c, x>3>, d, false, 0);
I:= otr(x>3>, a, false, 0);
I:= otr(x>4>, a, false, 0);
I:= con(x>2>, a, c, false, 0);
I:= con (c, b, e, false, 0);
I:= diz (d, e, rez, false, 0);
If sohr then begin
rez.number:=newnumber;
rez.stroka:=t;
end;
y1:=rez.znachenie;
end;
Отмоделировать функцию лучше программным путем, т. к. программу довольно просто модифицировать.
3.12.2.2 Конечные автоматы с памятью (последовательностные)
Для таких автоматов характерно наличие вектора внутренних состояний z=(z>1>, z>2>,…, z>m>>).>
В таких автоматах каждая логическая функция зависит от входных функций x и функций внутреннего состояния z.

Рис. 10. Конечный автомат с памятью

 . (8)
. (8)
Для автоматов с
памятью характерно, что они функционируют
во времени, и в момент времени t>0>
должно быть задано начальное состояние
z>0>.
В момент времени t>0>
 определяется выражением (8). В момент
времени t>1>=t>0>+
входной вектор может поменяться, в свою
очередь может поменяться вектор состояний
Y.
определяется выражением (8). В момент
времени t>1>=t>0>+
входной вектор может поменяться, в свою
очередь может поменяться вектор состояний
Y.
 , (9)
, (9)
где – такт логического конечного автомата. Считается, что много больше времени расчета на ЭВМ.
Пример.
Та же самая экспертная система определения профессиональной пригодности, но с условием, что значение о профессиональной пригодности зависит от ранее полученных ответов. Такие экспертные системы называют самообучающимися, т. к. сразу правильного ответа не дают. Частным случаем конечного автомата с памятью является автомат с обратной связью по выходу. Для него вектор внутренних состояний в момент времени t+ равен вектору выходных сообщений в момент времени t. Пример конечного автомата с памятью и обратной связью по выходу приведен на рис. 11.

Рис. 11. Конечный автомат с памятью и обратной связью по выходу
Экспертная система является примером конечного автомата с памятью с обратной связью по выходу. Программная модель такого автомата базируется на программной модели автомата без памяти, однако, помимо уже накопленного опыта добавляется процедура tact, а также начальные значения входных и выходных переменных.
Const
N=…; k=…;
Type
Vector x = array [1..n] of boolean;
Vector y = array [1..k] of boolean;
Var
X: vector X;
Ypred, Y: vector Y;
Procedure tact (v: vector X; var Ypred, Y: vector Y);
Var
I: integer;
Begin
Y[1]:=y>1>(…);
Y[2]:=y>2>(…);
Y[3]:=y>3>(…);
Y[k]:=y>k>(…);
For i:=1 to k do
Ypred[i]:= Y[i];
End;
End.
Состояние конечного автомата называется установившимся, если с течением времени при постоянном значении входного вектора Х, вектор Y принимает постоянное значение. В этом случае процесс обучения конечного автомата заканчивается, и результаты его работы могут быть использованы. Однако существуют автоматы, состояние которых не устанавливается с течением времени. Такие автоматы используются только в схемотехнике. Примером такого автомата является автомат триггерного типа. Логическая схема триггера приведена на рис. 12.

Рис. 12. Автомат триггерного типа
Другим
частным случаем является автономный
конечный автомат, для которого вектор
входных воздействий
 отсутствует. Для него вектор выходных
состояний является функцией от вектора
внутренних состояний
отсутствует. Для него вектор выходных
состояний является функцией от вектора
внутренних состояний
 .
Для него
.
Для него
 (с
обратной связью по выходу), тогда
(с
обратной связью по выходу), тогда
 .
Такие конечные автоматы называют также
генераторами высказываний или генераторами
логической последовательности. Они
могут использоваться для отладки и
моделирования некоторых ситуаций.
.
Такие конечные автоматы называют также
генераторами высказываний или генераторами
логической последовательности. Они
могут использоваться для отладки и
моделирования некоторых ситуаций.
Контрольные вопросы
1. Что такое логический конечный автомат?
2. Представьте в виде рисунка логический конечный автомат.
3. Что такое такт конечного логического автомата?
4. Приведите пример конечного автомата без памяти.
5. Приведите пример конечного автомата с памятью.
6. Приведите пример конечного автомата с обратной связью по выходу.
Библиографический список
Акимов В.А. Дискретная математика: логика, группы, графы. М.: Лаборатория Базовых Знаний, 2003, 376 с.
Стол Роберт Р. Множества. Логика. Аксиоматические теории. Пер. с англ. Ю.А. Гастева И.Х. Шмаина. Под ред. Ю.А. Шихановича. М., «Просвещение», 1968, 232 с.
Ершов Ю.А., Полюнин Е.А. Математическая логика: Учебное пособие для вузов. М.: Наука. Гл. ред. физ. – мат. лит., 1987, 336 с.
Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Высшая школа, 2003, 256 с.
Р. Хаггарти Дискретная математика для программистов Москва: Техносфера, 2003, 320 с.
Гончарова Г.А., Мочалин А.А. Элементы дискретной математики: Учебное пособие. – М.: ФОРУМ: ИНФРА-М, 2004, 128 с.
7. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики: Учебник. – М.: ИНФРА – М; Новосибирск: НГТУ, 2003, 280 с. – (Серия «Высшее образование»)
8. Новиков Ф.А. Дискретная математика для программистов. – СПб: Питер, 2001, 304 с.: ил.
 p
p















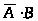
































 ;
;
 ;
;
 ;
; ;
; ;
;

 ;
; ;
;

 }
– базис Пирса
}
– базис Пирса












