Графы. Основные понятия
Министерство образования и науки Российской Федерации
Курский государственный технический университет
Кафедра ПО ВТ и АС
Лабораторная работа № 1
Графы. Основные понятия
Выполнил: студент гр. ПО 62 Шиляков И.А.
Проверил: доцентТомакова Р.А.
Курск 2007
Задание:
По заданным матрицам смежности вершин восстановить графы.
Построить для каждого графа матрицу смежности ребер, инцидентности, достижимости, контрдостижимости.
Найти и построить объединение, пересечение, кольцевую сумму заданных графов.
Найти композицию графов >
>
>
>.Для каждого графа найти и построить остовный подграф, произвольный подграф, порожденный подграф.
Определить локальные степени вершин графа, проверить существует ли в данном графе эйлерова цепь, эйлеров цикл.
Определить хроматические и цикломатические числа данных графов.
Найти все базы графа.
Определить в каждом графе сильные компоненты связности, построить конденсацию графа.
Выполнение:
По заданным матрицам смежности вершин восстановить графы.
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
|
|
x>1> |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
x>2> |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
x>3> |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
x>4> |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
x>5> |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
x>6> |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
x>7> |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
A>1>
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
G>1>(X>1>,A>1>)
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
|
|
x>1> |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
x>2> |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
x>3> |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
x>4> |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
x>5> |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
x>6> |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
x>7> |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
A>2>
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
G>2>(X>2>,A>2>)
Построить для каждого графа матрицу смежности ребер, инцидентности, достижимости, контрдостижимости.
-
а>1>
а>2>
а>3>
а>4>
а>5>
а>6>
а>7>
а>8>
а>9>
а>10>
а>11>
а>12>
а>13>
а>14>
а>1>
0
1
1
1
1
0
1
0
1
0
0
0
0
0
а>2>
1
0
0
0
0
0
1
0
1
1
0
0
1
1
а>3>
1
0
0
1
1
1
0
0
0
0
1
0
0
0
а>4>
1
0
1
0
1
0
0
0
0
0
1
1
0
1
а>5>
1
0
1
1
0
1
0
0
0
0
1
0
0
0
а>6>
0
0
1
0
1
0
1
1
0
0
1
1
0
0
а>7>
1
1
0
0
0
1
0
1
1
0
0
1
0
0
а>8>
0
0
0
0
0
1
1
0
1
1
0
1
1
0
а>9>
1
1
0
0
0
0
1
1
0
1
0
0
1
0
а>10>
0
1
0
0
0
0
0
1
1
0
0
0
1
1
а>11>
0
0
1
1
1
1
0
0
0
0
0
1
0
1
а>12>
0
0
0
1
0
1
1
1
0
0
1
0
0
1
а>13>
0
1
0
0
0
0
0
1
1
1
0
0
0
1
а>14>
0
1
0
1
0
0
0
0
0
1
1
1
1
0
B>1>
-
а>1 >
а>2>
а>3>
а>4>
а>5>
а>6>
а>7>
а>8>
а>9>
а>10>
а>11>
а>12>
а>13>
а>14>
а>1>
0
1
0
1
1
1
1
0
1
0
0
0
0
0
а>2>
1
0
1
1
1
1
0
1
0
0
0
0
0
0
а>3>
0
1
0
1
0
0
1
1
0
0
0
1
1
0
а>4>
1
1
1
0
0
0
1
1
1
0
0
0
0
0
а>5>
1
1
0
0
0
1
0
0
0
1
1
0
0
0
а>6>
1
1
0
0
1
0
0
0
0
1
1
0
0
0
а>7>
1
0
1
1
0
0
0
0
1
0
0
1
1
0
а>8>
0
1
1
1
0
0
0
0
0
0
1
0
1
1
а>9>
1
0
0
1
0
0
1
0
0
1
0
1
0
1
а>10>
0
0
0
0
1
1
0
0
1
0
1
1
0
1
а>11>
0
0
0
0
1
1
0
1
0
1
0
0
1
1
а>12>
0
0
1
0
0
0
1
0
1
1
0
0
1
1
а>13>
0
0
1
0
0
0
1
1
0
0
1
1
0
1
а>14>
0
0
0
0
0
0
0
1
1
1
1
1
1
0
B>2>
|
а>1 > |
а>2> |
а>3> |
а>4> |
а>5> |
а>6> |
а>7> |
а>8> |
а>9> |
а>10> |
а>11> |
а>12> |
а>13> |
а>14> |
|
|
x>1> |
1 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
|
x>2> |
-1 |
0 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
x>3> |
0 |
0 |
-1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
|
x>4> |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
1 |
0 |
0 |
0 |
-1 |
0 |
0 |
|
x>5> |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
1 |
0 |
0 |
-1 |
0 |
|
x>6> |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
-1 |
|
x>7> |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
1 |
S>1>
|
а>1 > |
а>2> |
а>3> |
а>4> |
а>5> |
а>6> |
а>7> |
а>8> |
а>9> |
а>10> |
а>11> |
а>12> |
а>13> |
а>14> |
|
|
x>1> |
1 |
0 |
0 |
1 |
0 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
|
x>2> |
0 |
-1 |
1 |
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
x>3> |
-1 |
1 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
x>4> |
0 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
|
x>5> |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
1 |
0 |
-1 |
1 |
|
x>6> |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
1 |
0 |
-1 |
|
x>7> |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
S>2>
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
|
|
x>1> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>2> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>3> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>4> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>5> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>6> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>7> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
|
|
x>1> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>2> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>3> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>4> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>5> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>6> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>7> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
R>1 >R>2>
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
|
|
x>1> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>2> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>3> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>4> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>5> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>6> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>7> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>1> |
x>2> |
x>3> |
x>4> |
x>5> |
x>6> |
x>7> |
|
|
x>1> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>2> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>3> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>4> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>5> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>6> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x>7> |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Q>1 >Q>2 >
Найти и построить объединение, пересечение, кольцевую сумму заданных графов.
Объединение графов
>0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000>
G>3>(X>3>,A>3>)=G>1>(X>1>,A>1>) YG>2>(X>2>,A>2>); X>3>= X>1>YX>2, >A>3>= A>1>YA>2>
Пересечение графов
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
G>3>(X>3>,A>3>)=G>1>(X>1>,A>1>) ∩G>2>(X>2>,A>2>); X>3>= X>1>∩X>2, >A>3>= A>1>∩A>2>
Кольцевая сумма графов
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
G>3>(X>3>,A>3>)=G>1>(X>1>,A>1>)>
>G>2>(X>2>,A>2>)
Найти и построить композицию графов >
>
>
>.
|
G>1>(Х) |
G>2>(Х) |
G>1>(G>2>(Х)) |
G>2>(G>1>(Х)) |
|
|
x>1> |
(x>1>,x>2>), (x>1>,x>7>) |
(x>1>,x>2>), (x>1>,x>3>) |
(x>1>,x>3>), (x>1>,x>6>), (x>1>,x>2>), (x>1>,x>4>), |
(x>1>,x>4>), (x>1>,x>5>), (x>1>,x>3>), (x>1>,x>6>), |
|
x>2> |
(x>2>,x>3>), (x>2>,x>6>) |
(x>2>,x>4>), (x>2>,x>5>) |
(x>2>,x>1>), (x>2>,x>5>), (x>2>,x>7>), |
(x>2>,x>2>), (x>2>,x>7>), (x>2>,x>1>), (x>2>,x>4>), |
|
x>3> |
(x>3>,x>2>), (x>3>,x>4>) |
(x>3>,x>2>), (x>3>,x>7>) |
(x>3>,x>3>), (x>3>,x>6>), (x>3>,x>5>), |
(x>3>,x>4>), (x>3>,x>5>), (x>3>,x>1>), |
|
x>4> |
(x>4>,x>1>), (x>4>,x>5>) |
(x>4>,x>1>), (x>4>,x>5>) |
(x>4>,x>2>), (x>4>,x>7>), (x>4>,x>1>), |
(x>4>,x>2>), (x>4>,x>3>), (x>4>,x>6>), (x>4>,x>7>), |
|
x>5> |
(x>5>,x>1>), (x>5>,x>7>) |
(x>5>,x>6>), (x>5>,x>7>) |
(x>5>,x>3>), (x>5>,x>4>), (x>5>,x>5>), (x>5>,x>6>), |
(x>5>,x>2>), (x>5>,x>3>), (x>5>,x>6>), |
|
x>6> |
(x>6>,x>3>), (x>6>,x>4>) |
(x>6>,x>1>), (x>6>,x>4>) |
(x>6>,x>2>), (x>6>,x>7>), (x>6>,x>1>), (x>6>,x>5>), |
(x>6>,x>2>), (x>6>,x>7>), (x>6>,x>1>), (x>6>,x>5>), |
|
x>7> |
(x>7>,x>5>), (x>7>,x>6>) |
(x>7>,x>3>), (x>7>,x>6>) |
(x>7>,x>2>), (x>7>,x>4>), (x>7>,x>3>), |
(x>7>,x>6>), (x>7>,x>7>), (x>7>,x>1>), (x>7>,x>4>), |
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000G>1>(G>2>(Х))
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
G>2>(G>1>(Х))
Для каждого графа найти и построить остовный подграф, произвольный подграф, порожденный подграф.
Остовные подграфы
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
G’>1>(X>1>,A>1>)
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
G’>2>(X>2>,A>2>)
Произвольные подграфы
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
G>1>’’ (X>1>’’,A>1>’’)
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
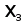G>2>’’
(X>2>’’,A>2>’’)
Порожденные подграфы
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
G>1P>(X>1P>,A>1P>) G>2P>(X>2P>,A>2P>)
Определить локальные степени вершин графа, проверить существует ли в данном графе эйлерова цепь, эйлеров цикл.
Локальные степени графа G>1>
>
>>1>
(х>1>)=2 ; >>>2>
(х>1>)=2 ; >>
(х>1>)=4 ;
>>>1>
(х>2>)=2 ; >>>2>
(х>2>)=2 ; >>
(х>2>)=4 ;
>>>1>
(х>3>)=2 ; >>>2>
(х>3>)=2 ; >>
(х>3>)=4 ;
>>>1>
(х>4>)=2 ; >>>2>
(х>4>)=2 ; >>
(х>4>)=4 ;
>>>1>
(х>5>)=2 ; >>>2>
(х>5>)=2 ; >>
(х>5>)=4 ;
>>>1>
(х>6>)=2 ; >>>2>
(х>6>)=2 ; >>
(х>6>)=4 ;
>>>1>
(х>7>)=2 ; >>>2>
(х>7>)=2 ; >>
(х>7>)=4 ;
Локальные степени графа G>2>
>>>1>
(х>1>)=2 ; >>>2>
(х>1>)=2 ; >>
(х>1>)=4 ;
>>>1>
(х>2>)=2 ; >>>2>
(х>2>)=2 ; >>
(х>2>)=4 ;
>>>1>
(х>3>)=3 ; >>>2>
(х>3>)=2 ; >>
(х>3>)=4 ;
>>>1>
(х>4>)=2 ; >>>2>
(х>4>)=2 ; >>
(х>4>)=4 ;
>>>1>
(х>5>)=2 ; >>>2>
(х>5>)=2 ; >>
(х>5>)=4 ;
>>>1>
(х>6>)=2 ; >>>2>
(х>6>)=2 ; >>
(х>6>)=4 ;
>>>1>
(х>7>)=2 ; >>>2>
(х>7>)=2 ; >>
(х>7>)=4 ;
Эйлерова цепь существует в двух графах, т.к. все локальные степени графов четны.
Эйлеров цикл существует в двух графах, т.к. все локальные степени графов четны.
Определить хроматические и цикломатические числа данных графов.
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
Хроматическое число γ для графа G>1> = 4
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
Хроматическое число γ для графа G>2> = 4
Цикломатические числа графов
V(G>1>)=m-n+r, где m - число рёбер (дуг);
n – число вершин;
r – число компонент связности.
V(G>1>)=14-7+1=8;
V(G>2>)=14-7+1=8;
Найти все базы графа.
Базы графа G>1 >
B>1>={x>1>}
B>2>={x>2>}
B>3>={x>3>}
B>4>={x>4>}
B>5>={x>5>}
B>6>={x>6>}
B>7>={x>7>}
Базы графа G>2 >
B>1>={x>1>}
B>2>={x>2>}
B>3>={x>3>}
B>4>={x>4>}
B>5>={x>5>}
B>6>={x>6>}
B>7>={x>7>}
Определить в каждом графе сильные компоненты связности, построить конденсацию графа.
Сильные компоненты связности G>1>
СК={x>1>, x>2>, x>3>, x>4>, x>5>, x>6>, x>7>}
Сильные компоненты связности G>2 >
СК={x>1>, x>2>, x>3>, x>4>, x>5>, x>6>, x>7>}
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d0100000300000000000100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010009f30000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000a41f0000b80b000020454d4600000100180300001200000002000000000000000000000000000000000500002003000040010000c800000000000000000000000000000000e20400400d0300160000000c000000180000000a00000010000000000000000000000009000000100000004401000078000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100b0ae11001000000014b2110094af11005251603214b211000caf1100100000007cb01100f8b111002451603214b211000caf11002000000049642f310caf110014b2110020000000ffffffffcc43d300d0642f31ffffffffffff0180ffff01809f020180ffffffff00a907000008000000080000014a250001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c0069006200720000000000410e0000d4af1100dee32e31e88d083234b3110040af11009c38273106000000010000007caf11007caf1100e878253106000000a4af1100cc43d3006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000000000c8410000c841000000000d000000010000004c000000040000000000000000000000440100007800000050000000200008000900000046000000280000001c0000004744494302000000ffffffffffffffff4501000079000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c0278004401040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000004401780020390900040000002d010000040000002d010000030000000000
Конденсация графа G>1 >Конденсация графа G>2 >