Высшая математика (работа 6)
Задача 1
Провести полное исследование функций и построить их графики
>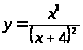 >
>
Решение:
1)
Область определения >
 >,функция
общего вида, т.к.
>,функция
общего вида, т.к.
y(-x)≠-y(x), y(-x)≠y(x);
2)
>
 >
=>x=-4
>
=>x=-4
точка разрыва 2-го рода
3)
Нули функции >
 >
>
4) Интервалы монотонности
> >
>
>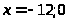 >
возможные точки экстремума
>
возможные точки экстремума
> >не
существует при >
>не
существует при >
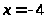 >
>
-
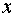

-12

4

0



0

-

0

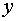

-27

-

0

Функция возрастает при
> >.
>.
Функция
убывает при >
 >.
>.
> >–
точка максимума.
>–
точка максимума.
5. Выпуклость и вогнутость кривой.
> >
>
> >
при >
>
при >
 >
>
>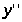 >не
существует при >
>не
существует при >
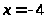 >
>
при
>
 >
кривая выпукла
>
кривая выпукла
при
>
 >
кривая вогнута
>
кривая вогнута
> >
тч. перегиба
>
тч. перегиба
6) Асимптоты.
а) вертикальные: х=-4.
б) наклонные:
> >,
>
>,
>
 >=>
>=>
> >
>
– наклонная асимптота
7) График функции

Задача 2
Фирма планирует собирать S шт./год телевизоров. Она периодически закупает кинескопы одинаковыми партиями размером q , шт./партию. Издержки по поставке не зависят от размера партии и равны С>П>, руб./поставку. Хранение одного кинескопа на складе в течение года обходится в С>Х>. руб./шт. год. Сборка телевизоров производится равномерно, с постоянной интенсивностью. Требуется определить оптимальные параметры системы снабжения кинескопами, при которых суммарные годовые издержки пополнения и хранения запаса кинескопов минимальны.
Таблица 1 - Параметры системы снабжения фирмы кинескопами
-
№
S
С>П>
С>Х>
12
62000
1650
68
Указания к задаче 2:
1) Запишите формулы для годовых издержек пополнения запасов И>П>(q), издержек хранения И>Х>(q) и суммарных издержек И(q) → min;
2) Сформулируйте критерий нахождения экстремума суммарных издержек;
3) Рассчитайте оптимальные значения параметров системы (партия поставок q, число поставок в год Nо, период между поставками То, издержки пополнения И>П>о, издержки хранения И>Х>о , суммарные издержки Ио);
4) Постройте график изменения текущего запаса кинескопов в течение года;
5) Исследуйте характер изменения трех видов издержек как функций размера партииq и постройте графики этих функций на новом рисунке.
Решение:
Годовые издержки пополнения запасов И>П> можно определить как произведение числа поставок N на стоимость одной поставки С>П>.
И>П> = N * С>П>
Число поставок можно выразить через общий объем поставок S и размер партии q:
N
= >
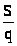 >
>
Тогда можно записать функцию годовых издержек пополнения запасов в зависимости от размера партии:
И>П>(q)
= С>П>
* >
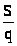 >
>
Функцию годовых издержек хранения И>Х> можно определить как произведение стоимости хранения единицы С>Х> на среднее число кинескопов на складе.
Среднее число единиц хранения при равномерном расходе определяется как полусумма максимального и минимального числа кинескопов. Примем за минимальный уровень нулевое значение (без страхового запаса). Тогда максимальный уровень будет равен размеру партии, т.к. сразу после поставки на складе будет лежать q кинескопов.
Исходя из вышесказанного, можно записать функцию годовых издержек хранения:
И>Х>(q)
= C>X>
* >
 >
= C>X>
* >
>
= C>X>
* >
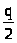 >
>
Запишем функцию суммарных издержек:
И(q)
= И>П>(q)
+ И>Х>(q)
= С>П>
* >
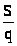 >
+ C>X>
* >
>
+ C>X>
* >
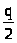 >
>
Экстремум функции суммарных издержек от размера партии определим из условия равенства нулю первой производной. Это экстремум соответствует минимуму суммарных издержек и определяет оптимальный размер партии.
И’(q)
= (С>П>
* >
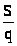 >
+ C>X>
* >
>
+ C>X>
* >
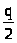 >)’=
– >
>)’=
– >
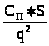 >
+ >
>
+ >
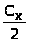 >
>
Составим и решим уравнение:
– >
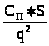 >
+ >
>
+ >
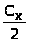 >
= 0 ; >
>
= 0 ; >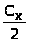 >
= >
>
= >
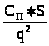 >
; q2
= >
>
; q2
= >
 >
; q
= >
>
; q
= >
 >.
>.
Отрицательное значение корня не имеет физического смысла.
В результате получили формулу для определения оптимального размера партии.
Рассчитаем оптимальные значения параметров системы.
Найдем оптимальный размер партии:
q
= >
 >
= >
>
= >
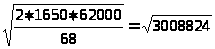 >
»
1735 шт.
>
»
1735 шт.
Найдем число поставок в год:
Nо = S / q = 62000 / 1735 = 35,7 » 36 раз
Найдем период между поставками:
То = 360 / 36 = 10 дней
Найдем издержки пополнения:
И>П>о = С>П> * N = 1650 * 36 = 59400 руб.
Найдем издержки хранения:
И>Х>о
= C>X>
* >
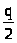 >
= 68 * 1735 / 2 = 58990 руб.
>
= 68 * 1735 / 2 = 58990 руб.
Найдем суммарные издержки
Ио = И>П>о + И>Х>о = 59400 + 58990 = 118390 руб.
Построим график запасов:
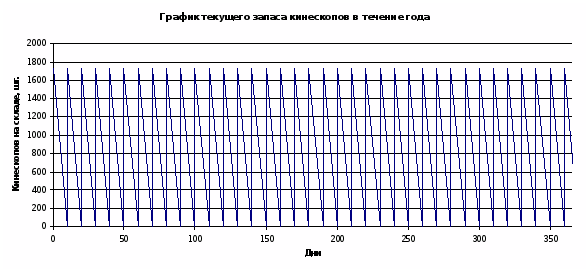
Рис. 1
Рассмотрим функции издержек.
Годовые
издержки пополнения запасов И>П>(q)
= С>П> * >
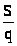 >
являются обратной гиперболической
функцией, которая монотонно убывает с
увеличением размера партии q.
С возрастанием q скорость
убывания падает.
>
являются обратной гиперболической
функцией, которая монотонно убывает с
увеличением размера партии q.
С возрастанием q скорость
убывания падает.
Годовые
издержки хранения И>Х>(q)
= C>X> *
>
 >
являются линейной функцией, которая
монотонно возрастает с увеличением
размера партии q. Минимальное
значение функции нулевое. С возрастанием
q скорость увеличения
издержек хранения не изменяется.
>
являются линейной функцией, которая
монотонно возрастает с увеличением
размера партии q. Минимальное
значение функции нулевое. С возрастанием
q скорость увеличения
издержек хранения не изменяется.
Суммарные издержки являются суммой двух предыдущих функций. В силу этого, функция сначала убывает – когда издержки пополнения запасов существенно выше издержек хранения, а после выравнивания размеров издержек начинает возрастать – когда издержки хранения превышают размер издержек пополнения. Функция суммарных издержек имеет один минимум в районе примерного равенства входящих в нее функций.
Построим графики изменения трех видов издержек как функций размера партииq:
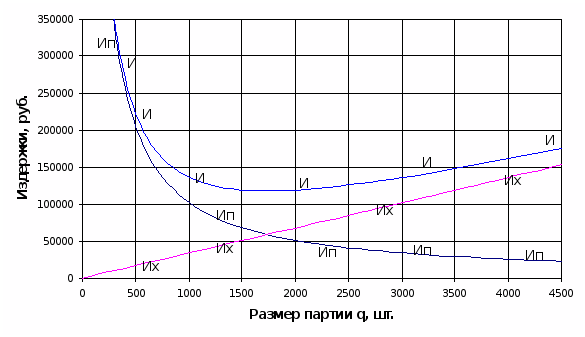
Рис..2
Задача 3
Фирма собрала сведения об объемах продаж своей продукции (Y>i>) за 6 последних месяцев (X>i> =1...6) и представила их в виде таблицы. Перед отделом маркетинга поставлена задача аппроксимировать эмпирические данные подходящей функцией, чтобы использовать ее для целей краткосрочного прогнозирования (на один и два месяца вперед, X>j>> >=7, 8).
Таблица 1 - Данные о помесячных объемах продаж фирмы
-
№
Y>1>
Y>2>
Y>3>
Y>4>
Y>5>
Y>6>
12
14
13
11
14
13
16
Указания к задаче 3:
1) выполните аппроксимацию эмпирических данных линейной функцией у = a>0>x + a>1>;
2) выведите нормальные уравнения метода наименьших квадратов для линейной функции;
3) выведите формулы Крамера для параметризации аппроксимирующей линейной функции;
4) для расчета параметров аппроксимирующей линейной функции составьте таблицу.
Таблица.2 - Параметризация аппроксимирующей линейной функции.
-
i
X>i>
Y>i>
X>i>2
X>i>Y>i>
1
2
3
4
5
6
Сумма
5) запишите выражение для аппроксимирующей линейной функции и рассчитайте ее значения о точках X>i> = 1...8; результаты расчетов оформите в виде таблицы;
6) изобразите на одном рисунке в большом масштабе график аппроксимирующей линейной функции и нанесите эмпирические точки.
Решение:
Аппроксимацию эмпирических данных будем выполнять линейной функцией
у = a>0>x + a>1>
Сущность
метода наименьших квадратов состоит в
подборе таких a>1>
и a>0>
, чтобы сумма квадратов отклонений была
минимальной. Так как каждое отклонение
зависит от отыскиваемых параметров, то
и сумма квадратов отклонений будет
функцией F
этих параметров: F(a>0>
, a>1>)
= >
 >
или F(a>0>
, a>1>)
= >
>
или F(a>0>
, a>1>)
= >
 >
>
Для отыскания минимума приравняем нулю частные производные по каждому параметру:
> >=
>
>=
>
 >
>
>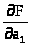 >=
>
>=
>
 >
>
Выполнив элементарные преобразования сумм, получим систему из двух линейных уравнений относительно a>1> и a>0>:
> >
>
Решим данную систему методом Крамера:
>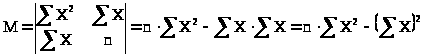 >
>
> >
>
> >
>
Тогда можно вывести формулы расчета параметров:
>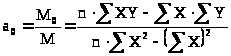 >
>
> >
>
Построим расчетную таблицу
Таблица 3 – Расчетная таблица
-
i
X>i>
Y>i>
X>i>2
X>i>Y>i>
1
1
14
1
14
2
2
13
4
26
3
3
11
9
33
4
4
14
16
56
5
5
13
25
65
6
6
16
36
96
Сумма
21
81
91
290
Найдем значения параметров:
> >
>
>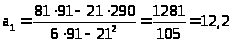 >
>
Тогда формула аппроксимирующей линейной функции будет равна
> >
= 0,3714·X>i>
+ 12,2
>
= 0,3714·X>i>
+ 12,2
Найдем значения аппроксимирующей функции:
Таблица 4 – Расчет значений аппроксимирующей функции
-
i
X>i>

1
1
12,5714
2
2
12,9428
3
3
13,3142
4
4
13,6856
5
5
14,057
6
6
14,4284
7
7
14,7998
8
8
15,1712
Построим график аппроксимирующей функции
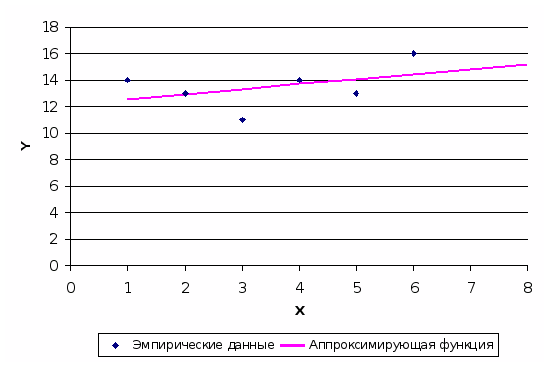
Рис.1
Задача 4
Найти приращение и дифференциал функции y=a>0>x3+a>1>x2+a>2>x (таблица). Рассчитать абсолютное и относительное отклонения dy от Δy.
Решение:
y=4x3–2x2–3x
Приращение функции
y(x+Δx)–y(x)= 4(x+Δx)3–2(x+Δx)2–3(x+Δx) – (4x3–2x2–3x)=
=4(x3+3x2Δx + 3xΔx2 + Δx3) –2(x2+2 xΔx +Δx2)–3x–3Δx –4x3+2x2+3x=
=4x3+12x2Δx + 12xΔx2 + 4Δx3 –2x2–4 xΔx –2Δx2–3Δx –4x3+2x2=
=12x2Δx + 12xΔx2 + 4Δx3–4 xΔx –2Δx2–3Δx =
=(12x2–4 x–3)Δx +((12x–2)Δx2 + 4Δx3)
Линейная по Δx часть приращения есть дифференциал, то есть
dy=(12x2–4 x–3)Δx или заменяя Δx на dx получим dy=(12x2–4 x–3)dx
Абсолютное отклонение:
Δy– dy = (12x2–4 x–3)Δx +((12x–2)Δx2 + 4Δx3)– (12x2–4 x–3)Δx =(12x–2)Δx2 + 4Δx3
Относительное отклонение:
>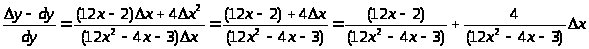 >
>
Задача 5
Используя
дифференциал, рассчитайте приближенное
значение функции >
 >,
оцените относительную погрешность и
вычислите значение с 6 знаками.
>,
оцените относительную погрешность и
вычислите значение с 6 знаками.
n=3, x=63
Решение:
>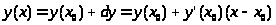 >
>
Возьмем
>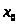 >=64
>=64
>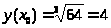 >
>
> >=>>
>=>> >
>
Тогда
>
 >
>
>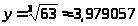 >
>
Относительная погрешность
> >
>
Задача 6. Найти неопределенные интегралы, используя метод разложения.
Решение:
1)
>
 >
>
2)
>
 >
>
Задача 7
Найти неопределенные интегралы, используя метод замены переменной.
Решение:
1)
>
 >2)>
>2)>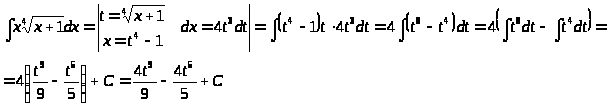 >
>
Задача 8
Найти неопределенные интегралы, используя метод интегрирования по частям.
Решение:
1)
>
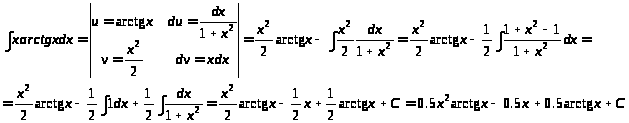 >
>
2)
>
 >
>
Задача 9. Нарисуйте прямоугольный треугольник с вершинами в точках О(0,0), А(а,0), В(0,b). Используя определенный интеграл выведите формулу площади прямоугольного треугольника.
Решение:
Уравнение гипотенузы найдем как уравнение прямой по 2-м точкам:
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010030910000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000021b0000df14000020454d4600000100180300001200000002000000000000000000000000000000900600001a040000b801000013010000000000000000000000000000c0b6060038320400160000000c000000180000000a000000100000000000000000000000090000001000000008010000cc000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100dc5f11001000000040631100c060110052516032406311003860110010000000a8611100246311002451603240631100386011002000000049642f31386011004063110020000000fffffffffc02e600d0642f31ffffffffffff0180ffff0180efff0180ffffffff0000000000080000000800004300000001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c00690062007200000000000000000000611100dee32e31e88d0832606411006c6011009c3827310800000001000000a8601100a8601100e878253108000000d0601100fc02e6006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000001886d1411886d141000000000d000000010000004c00000004000000000000000000000008010000cc000000500000002000ffff0900000046000000280000001c0000004744494302000000ffffffffffffffff09010000cd000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02cc000801040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000000801cc00204e0900040000002d010000040000002d010000030000000000
> >
=> >
>
=> >
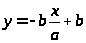 >
>
Тогда площадь треугольника равна:
> >
>
Задача 10. Нарисуйте треугольник произвольной формы, расположив его вершины в точках А>1>(а>1>,0), А>2>(а>2>,0), В(0,b). Используя определенный интеграл, выведите формулу площади треугольника произвольной формы.
Решение:
Уравнение сторон найдем как уравнения прямых по 2-м точкам:

А>1>В: >
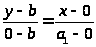 >
=> >
>
=> >
 >
>
А>2>В:
>
 >
=> >
>
=> >
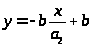 >
>
Тогда площадь треугольника равна:
> >
>
Задача 11. Начертите четверть круга радиуса R с центром в точке О(0,0). Используя определенный интеграл, выведите формулу площади круга. (Уравнение окружности x2+y2=R2)
Решение:



 0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010030910000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000021b0000df14000020454d4600000100180300001200000002000000000000000000000000000000900600001a040000b801000013010000000000000000000000000000c0b6060038320400160000000c000000180000000a000000100000000000000000000000090000001000000008010000cc000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100dc5f11001000000040631100c060110052516032406311003860110010000000a8611100246311002451603240631100386011002000000049642f31386011004063110020000000fffffffffc02e600d0642f31ffffffffffff0180ffff0180efff0180ffffffff0000000000080000000800004300000001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c00690062007200000000000000000000611100dee32e31e88d0832606411006c6011009c3827310800000001000000a8601100a8601100e878253108000000d0601100fc02e6006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000001886d1411886d141000000000d000000010000004c00000004000000000000000000000008010000cc000000500000002000ffff0900000046000000280000001c0000004744494302000000ffffffffffffffff09010000cd000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02cc000801040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000000801cc00204e0900040000002d010000040000002d010000030000000000
0100090000032a0200000200a20100000000a201000026060f003a03574d4643010000000000010030910000000001000000180300000000000018030000010000006c000000000000000000000008000000100000000000000000000000021b0000df14000020454d4600000100180300001200000002000000000000000000000000000000900600001a040000b801000013010000000000000000000000000000c0b6060038320400160000000c000000180000000a000000100000000000000000000000090000001000000008010000cc000000250000000c0000000e000080250000000c0000000e000080120000000c00000001000000520000007001000001000000f1ffffff00000000000000000000000090010000000000cc04400022430061006c006900620072006900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100dc5f11001000000040631100c060110052516032406311003860110010000000a8611100246311002451603240631100386011002000000049642f31386011004063110020000000fffffffffc02e600d0642f31ffffffffffff0180ffff0180efff0180ffffffff0000000000080000000800004300000001000000000000006000000025000000372e9001cc00020f0502020204030204ef0200a07b20004000000000000000009f00000000000000430061006c00690062007200000000000000000000611100dee32e31e88d0832606411006c6011009c3827310800000001000000a8601100a8601100e878253108000000d0601100fc02e6006476000800000000250000000c00000001000000250000000c00000001000000250000000c00000001000000180000000c00000000000002540000005400000000000000000000000800000010000000010000001886d1411886d141000000000d000000010000004c00000004000000000000000000000008010000cc000000500000002000ffff0900000046000000280000001c0000004744494302000000ffffffffffffffff09010000cd000000000000004600000014000000080000004744494303000000250000000c0000000e000080250000000c0000000e0000800e000000140000000000000010000000140000000400000003010800050000000b0200000000050000000c02cc000801040000002e0118001c000000fb021000070000000000bc02000000cc0102022253797374656d0000000000000000000000000000000000000000000000000000040000002d010000040000002d01000004000000020101001c000000fb02f1ff0000000000009001000000cc0440002243616c6962726900000000000000000000000000000000000000000000000000040000002d010100040000002d010100040000002d010100050000000902000000020d000000320a0d00000001000400000000000801cc00204e0900040000002d010000040000002d010000030000000000
Из уравнения окружности:
>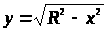 >
>
Тогда четверти круга равна:
> >
>
Тогда площадь круга равна:
>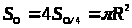 >
>
Задача 12
Используя определенный интеграл, вычислите площадь, ограниченную кривой y=lnx, осью ОХ и прямой х=е. Нарисуйте чертеж.
Решение:
Найдем
точки пересечения y=lnx
=0 (y=lnx с осью
ОХ: y=0)=>> >,
тогда искомая площадь:
>,
тогда искомая площадь:
> >
>

Задача 13
Вычислите площадь сегмента, отсекаемого прямой y=3–2x от параболы y=x2. Нарисуйте чертеж.
Решение:
Найдем точки
пересечения y=
x2
=3–2x
=> x2
+2x–3=0
=>> >,
тогда искомая площадь:
>,
тогда искомая площадь:
> >
>

Задача 14
Вычислить площадь между кривой y=1/x2 и осью ОХ, располагающуюся вправо от линии x=1. Нарисуйте чертеж.
Решение:
Искомая площадь:
>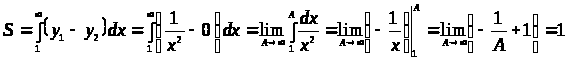 >
>

Вычислить
приближенное значение интеграла >
 >
по формуле трапеции, принимая n
= 5.
>
по формуле трапеции, принимая n
= 5.
Формула трапеций имеет вид
> >
>
Длина интервала
> >
>
Для удобства вычислений составим таблицу:
-
N

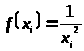
0
1
1,0000
1
2
0,2500
2
3
0,1111
3
4
0,0625
4
5
0,0400
5
6
0,0278
Тогда по формуле трапеций имеем:
> >
>
Точное значение
>
 >
>
Относительная погрешность
>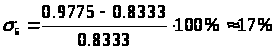 >
>
Повторим вычисления для 10 отрезков.
Длина интервала
> >
>
Для удобства вычислений составим таблицу:
-
N

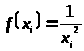
0
1
1,0000
1
1,5
0,4444
2
2
0,2500
3
2,5
0,1600
4
3
0,1111
5
3,5
0,0816
6
4
0,0625
7
4,5
0,0494
8
5
0,0400
9
5,5
0,0331
10
6
0,0278
Тогда по формуле трапеций имеем:
> >
>
Относительная погрешность
> >
>
Как видно, большее число разбиения дает более точный результат.
Задача 15. Решить дифференциальные уравнения с разделяющимися переменными.
Решение:
1)
>
 >
>
Разделим переменные
>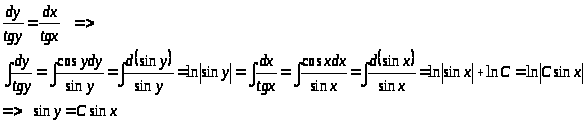 >
>
2) >
 >
>
Разделим переменные
> >
>
Задача 16
Преобразовать
дифференциальные уравнения к однородному
вида >
 >.
Выполнить замену y/x
и решить.
>.
Выполнить замену y/x
и решить.
Решение:
1)
>
 >
>
Разделим обе части на xy
>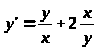 >
>
>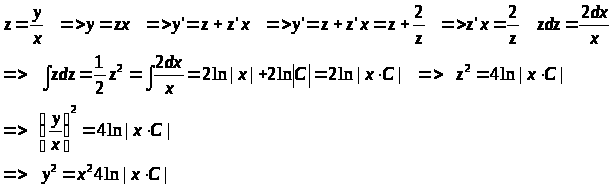 >2)
>
>2)
>
 >
>
Разделим обе части на x
> >
>
>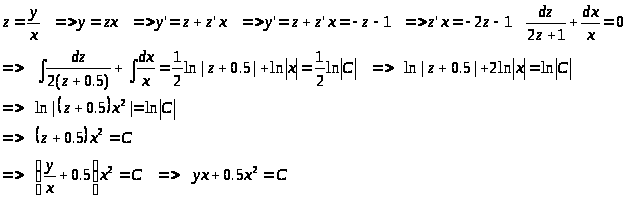 >
>
или
>
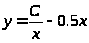 >
>
Задача 17
Привести
линейное дифференциальное уравнение
к виду >
 >
и решить его применив подстановку
y=u(x)∙v(x).
>
и решить его применив подстановку
y=u(x)∙v(x).
Решение:
1)
>
 >
>
Преобразуем
>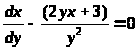 >
=> >
>
=> >
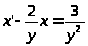 >
>
Пусть x=uv, тогда x′=u′v+uv′,
=>
>
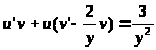 >=>
>
>=>
>
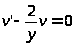 >,
>
>,
>
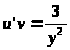 >,
>,
>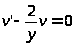 >
>
>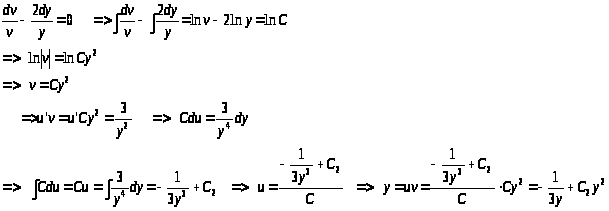 >>
>> >
>
2)
>
 >
>
Преобразуем
> >
=> >
>
=> >
 >
>
Пусть x=uv, тогда x′=u′v+uv′,
=>
>
 >=>
>
>=>
>
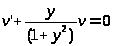 >,
>
>,
>
 >,
>,
>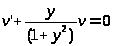 >>
>> >>
>> >
>
2)
>
 >
>
Разделим обе части на x
> >
>
>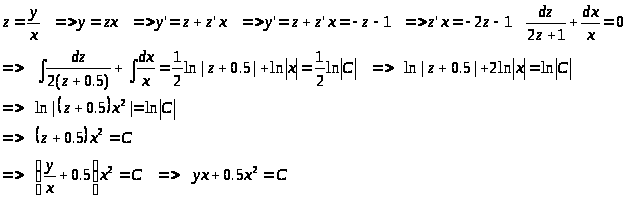 >
>
или
>
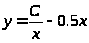 >
>
Задача 18
Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Решение:
1)
>
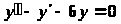 >
>
Запишем характеристическое уравнение:
λ2–λ–6=0 => λ>1,2>=3;-2 =>
Тогда общее решение дифференциального уравнения:
y = C>1>e3x + C>2>e–2x
2)> >
>
Найдем решение однородного дифференциального уравнения:
>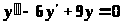 >
>
запишем характеристическое уравнение
: λ2–6λ+9=0 => λ>1,2>= 3 =>
y>0> = (C>1>+ C>2>x)e3x
Запишем частное решение по виду правой части:
ŷ = C>3>x2+ C>4>x+ C>5>
Найдем
ŷ ′ = 2C>3>x–C>4>
ŷ ′′ = 2C>3>
Подставим в исходное уравнение, получим:
2C>3> – 6(2C>3>x–C>4>)+9(C>3>x2+ C>4>x+ C>5>) =9C>3>x2+(9C>4>–12C>3>)x+(2C>3> + 6C>4>+9C>5>)= x2
=> C>3> = 1/9, => C>4> = 4/27, => C>5> = –10/81
> >
>
y
= y>0>
+ ŷ = (C>1>+
C>2>x)e3x
+
>
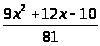 >
>