Асимптотика решений дифференциальных уравнений
Курсовая работа
по дисциплине “Эффективные алгоритмы исследования моделей естествознания”
на тему: «Асимптотические решения дифференциальных уравнений по малому параметру. Регулярные возмущения»
Содержание
Ведение
Применения регулярного возмущения
1. Асимптотическое поведение решений дифференциальных уравнений с малым параметром
1.1 Асимптотическое поведение решений системы
2. Регулярные возмущения
2.1 Асимптотические методы
2.2 Регулярные возмущения решений задачи Коши для обыкновенных дифференциальных уравнений
2.3 Существование решении возмущенной задачи
Литература
Ведение
Невозможно представить себе современную науку без широкого применения математического моделирования. Сущность этой методологии состоит в замене исходного объекта его «образом» — математической моделью — и дальнейшем изучении модели с помощью реализуемых на компьютерах вычислительно-логических алгоритмов. Этот «третий метод» познания, конструирования, проектирования сочетает в себе многие достоинства как теории, так и эксперимента. Работа не с самим объектом (явлением, процессом), а с его моделью дает возможность безболезненно, относительно быстро и без существенных затрат исследовать его свойства и поведение в любых мыслимых ситуациях (преимущества теории). В то же время вычислительные (компьютерные, симуляционные, имитационные) эксперименты с моделями объектов позволяют, опираясь на мощь современных вычислительных методов и технических инструментов информатики, подробно и глубоко изучать объекты в достаточной полноте, недоступной чисто теоретическим подходам (преимущества эксперимента).
Неудивительно, что методология математического моделирования бурно развивается, охватывая все новые сферы — от разработки технических систем и управления ими до анализа сложнейших экономических и социальных процессов.
Сейчас математическое моделирование вступает в третий принципиально важный этап своего развития, «встраиваясь» в структуры так называемого информационного общества.
Применения регулярного возмущения
Выходные пучки лазеров часто имеют квазирегулярную модуляцию волнового фронта (ВФ). В газовых лазерах с движущейся активной средой такую модуляцию могут вызывать неоднородности, возникающие под действием периодической сопловой решетки [1], под влиянием страт и доменов в газовом разряде [2], в результате наложения ударных волн [3,4], а также под действием ряда других физических факторов. Модуляция ВФ выходных лазерных пучков в литературе чаще всего рассматривается как фактор, влияющий, прежде всего на расходимость излучения.
Гораздо меньше внимания уделяется анализу метаморфоз структуры ВФ, условиям появления и взаимосвязи каустических и фазовых дислокационных образований в лазерных пучках. Такого рода образования регистрируются в излучении лазеров с самыми разными оптическими резонаторами [5,6]. В настоящей работе рассматриваются качественные изменения амплитудно-фазовой структуры лазерных пучков, первоначально обладающих плавной регулярной модуляцией ВФ.
Общее представление о характере рассматриваемых процессов можно получить на примере известной задачи [7] о распространении безграничной волны, фаза которой в начальной плоскости меняется по гармоническому закону. Амплитуда такой волны имеет следующий вид:
где m - параметр, характеризующий глубину фазовой модуляции; х - поперечная координата; а - период модуляции. На расстоянии z от начальной плоскости поле можно представить в виде суперпозиции плоских волн [7]:
где
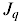- функция Бесселя порядка
-
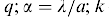волновое число. Это поле является частным
случаем самовоспроизводящихся полей,
свойства которых нашли применение в
лазерной технике [8,9]
Используя для расчета характеристик поля его разложение по плоским волнам (2), а также лучевой метод из работы [10], можно установить основные особенности трансформации первоначального распределения амплитуды и фазы. Расчеты показывают, что даже при малой глубине модуляции фазы и равномерном распределении интенсивности в начальной плоскости дифракционные эффекты приводят к значительному пространственному перераспределению интенсивности.
Перераспределение
наиболее заметно вблизи плоскостей
Эти плоскости располагаются между
плоскостями, в которых, согласно эффекту
Тальбо, воспроизводится первоначальное
равномерное распределение интенсивности.
Так, при m
= 0.1 контраст картины распределения
интенсивности
,
а при m
= 0.5 контраст К = 2.82. С превышением
определенной критической глубины
модуляции в структуре волны происходят
качественные изменения..
На рис.1
приведены распределения амплитуды А и
фазы Ф на расстояниях
при разных первоначальных глубинах
модуляции фазы. Видно, что при превышении
критической глубины модуляции появляются
линии с нулевыми амплитудами. В
распределении фазы им соответствуют
КД, обусловленные скачкообразным
изменением фазы на π. КД располагаются
симметрично относительно осей
клювообразных каустик. Клювы каустик,
находящиеся сначала вблизи плоскостей
,
с дальнейшим увеличением глубины фазовой
модуляции приближаются к плоскостям
воспроизведения первоначальной
структуры. При этом растет и число КД.
Их расположение по отношению к образующим каустик соответствует рассчитанной на основе интеграла Перси фазовой структуре поля, приведенной в работе [11].
Рис. 1.
Распределение амплитуды А (1,2) и фазы Ф
(3,4) по поперечной координате х для
безграничной волны на расстоянии
стрелками
указано положение клювов каустик.
Продольная структура распределения интенсивности излучения показана на рис. 2 для т = 1.2. Из него видно, что фазовая модуляция вызывает формирование каналов, вытянутых вдоль направления распространения, в которых интенсивность излучения существенно превышает среднюю. Оси этих областей совпадают с осями симметрии клювообразных каустик.
Если фазовая модуляция в начальной плоскости осуществляется не по одной а по двум поперечным координатам, то появляется возможность формирования винтовых дислокаций (ВД) волнового фронта. ВД отличаются от КД принципиально иной топологической структурой (при обходе вокруг ВД фаза меняется на 2п). На рис. 3,а приведена структура эквифазных линий ВФ в начальной плоскости когда распределение поля задается формулой
Здесь функция
)
совпадает с функцией
при
замене поперечной координаты х поперечной
координатой у С —константа.
Структура эквифазных линий в начальной плоскости на рис.3,а построена с помощью формулы (3) для С = 0.2 и m = 2. Ход линий свидетельствует о наличии плавных регулярных возмущений волнового фронта. На рис.3,6 изображена структура эквифазных линий на расстояниях
ВД располагаются в точках пересечения эквифазных линий. Они образуют своеобразные квадруполи каждый из которых состоит из четырех ВД. Две из них имеют положительный знак (являются «правыми»), две - отрицательный знак (являются «левыми»). Квадруполи окружают оси каустик.
В отличие от
КД каждая из которых строго говоря
формируется в определенной плоскости
z = const, ВД характеризуются определенной
продольной длиной. Как и КД дислокации
винтового типа возникают лишь при
превышении глубиной первоначальной
модуляции волнового фронта некоторого
критического значения. Если обозначить
через
разность
между максимальной и минимальной фазами
в начальной плоскости (при модуляции
по одной координате
совпадает с ni) то ВД будут возникать
когда
>
Все вышеперечисленные эффекты были проанализированы применительно к пространственно-ограниченному пучку с гауссовым профилем распределения интенсивности. В основу расчета была положена формула (2), в которой суперпозиция плоских волн была заменена системой распространяющихся под углом друг к другу raусовых мод свободного пространства [12]. Горловины мод располагались в начальной плоскости
Расчеты
показали, что переход к более точной
модели гауссова пучка с периодической
модуляцией ВФ не вносит существенных
качественных изменений в данные о
преобразовании амплитудно-фазового
распределения, по крайней мере на
расстояниях сопоставимых с характерной
длиной
.
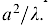Как и в случае безграничной волны
дислокации ВФ начинают формироваться
в ближней зоне, когда глубина модуляции
фазы превышает
.
Сказанное иллюстрирует рис. 4, который
является аналогом рис. 1 для гауссова
пучка. Отношение радиуса пучка в горловине
к периоду модуляции, а
равно пяти.
Из сравнения
рис. 1 и 4 видно, что имеющиеся в них
различия проявляются в дифракционном
«замывании» части дислокаций. Различия
усиливаются с ростом координаты z по
мере того, как ухудшается периодическая
воспроизводимость первоначальной
структуры поля. Это видно, в частности,
из рис. 5, на котором изображено продольное
распределение интенсивности для
параметров
Распределения, приведенные на рис.2 и 5, близки лишь в ближней зоне, для которой характерны узкие зоны, где концентрируется энергия светового потока. В дальней зоне дифракции перекрытие гауссовых угловых компонент излучения ослабевает, и структура излучения кардинальным образом отличается от структуры безграничной волны: излучение представляет собой «веер» пучков, интенсивность которых убывает с увеличением угла наклона.
Фазовая модуляция гауссова пучка по двум поперечным координатам, если ее глубина превышает указанную выше критическую глубину, приводит к появлению на волновом фронте БД. Как и в безграничной волне, эти БД обладают определенной продольной длиной, увеличивающейся с ростом глубины модуляции. Это свойство БД значительно облегчает их экспериментальное обнаружение. В дальней зоне дифракции вследствие изменения фазы в начальной плоскости по двум координатам будут формироваться два веера пучков, располагающихся во взаимно перпендикулярных плоскостях.
Заметим в заключение, что результаты выполненного анализа могут быть частично перенесены и на случай нерегулярной плавной модуляции ВФ, если длина рассматриваемой пространственной области сопоставима с величиной аЦк, где ап - характерный размер нерегулярных возмущений ВФ. В частности, это относится к образованию в световом поле каналов с повышенной интенсивностью и к появлению дислокаций волнового фронта при превышении фазовыми возмущениями определенного значения.
Таким образом, плавные возмущения ВФ играют важную роль в трансформации амплитудно-фазового профиля излучения и в формировании каустических и дислокационных образований. Появление каустик и дислокаций волнового фронта носит пороговый характер и непосредственно связано с глубиной первоначальной модуляции фазы. Для практики важным является то, что появление указанных образований в лазерном пучке сопряжено с формированием узких каналов, в которых интенсивность излучения значительно превышает среднюю.
Работа выполнена при финансовой поддержке государственной научно-технической программы «Физика квантовых и волновых процессов» (проект 1.61) и физического учебно-научного центра «Фундаментальная оптика и спектроскопия».
1. Асимптотическое поведение решений дифференциальных уравнений с малым параметром
Многие колебательные системы описываются дифференциальными уравнениями с малым параметром при производных:
или, в векторной форме
где
— малый положительный параметр,
—
неизвестные функции времени t,
характеризующие данную систему.
В работах (х) — (5) находится асимптотика решений системы (1.1) в случае, когда при каждом z любое решение системы «быстрых движений» **
при
приближается
либо к устойчивому положению равновесия,
либо к устойчивому предельному циклу.
Но возможны случаи, когда система «быстрых движений» (1.2) может не иметь асимптотически устойчивых положений равновесия и изолированных предельных циклов. Такова, например, гамильтонова система. Целью настоящей работы и является изучение этих случаев. Так, в § 2 с точностью до величин порядка О (г) находится решение системы (1.1), для которой соответствующая система «быстрых движений» гамильтонова и к = 2, т. е. находится решение системы
Асимптотические формулы для решения этой системы находятся для области, где траектории соответствующей гамильтоновой системы «быстрых движений» при каждом векторе z замкнуты (в случае невырожденного центра в рассматриваемую область включается и сам центр). Метод исследования системы (1.3) таков: сначала рассматривается система «быстрых движений» (1.4), а затем система (1.3) после соответствующей замены переменных усредняется вдоль решений (1.4). Оказывается, что уравнение с малым параметром и. при старшей производной и с пропущенной в основном члене Q (п — 1)-й производной, исследованное В.М. Волосовым (при п — 2 — в работе (12Г), при F ~ О — в 'работах (8) — (п)) методом конечных разностей, является частным случаем системы (1.3). Поэтому результаты работ (8) — (12) (эти результаты сформулированы в § 3 настоящей работы) следуют из результатов § 2.
Метод построения решения уравнения (1.5) при п = 2 с любой наперед заданной точностью в случае, когда известно общее решение (в форме разложения в тригонометрический ряд Фурье) соответствующего невозмущенного уравнения был дан в работе Ю.А. Митрополъским.
Задача исследования системы (1.3) с точки зрения работ (3) — (4) и вывода из нее известных результатов В.М. Волосова [работы (8) — (12)] относительно уравнения (1.5) была поставлена Л.С. Понтрягиным в его докладе на семинаре В.И. Смирнова в Ленинграде в середине апреля 1957 г.
Выражаю глубокую благодарность Л.С. Понтрягину за ценные указания, советы и постоянное внимание к настоящей работе.
1.1 Асимптотическое поведение решений системы
Система (1.3) в векторной форме имеет вид:
глк, в быстром времени
При е = 0 система (2.1') переходит в гамильтонову систему
являющуюся системой «быстрых движений» для системы (2.1). 1. Изучение системы (2.2). Пусть функции
определены и непрерывны вместе со всеми своими первыми частными производными в некоторой области G эвклидова пространства E>2>+i переменных х, у, zi,..., zi. Как известно, система (2.2) имеет первый интеграл
и (2.3) представляет собой семейство всех фазовых траекторий системы(2.2) на кажтгой плоскости z = const области G.
Возьмем некоторую точку (х, у, z) из G, не являющуюся положением равновесия системы (2.2). По известной теореме существования и единственности решений системы обыкновенных дифференциальных уравнений, через эту точку пройдет только одна фазовая траектория системы
(2.2). Уравнение этой траектории запишется в виде:
(см. (2.3)).
Докажем следующее утверждение.
Пусть траектория (2.4) замкнута и целиком лежит внутри области G. Тогда в пространстве E>2>+i существует некоторая окрестность G этой траектории (2.4) такая, что
фазовые траектории системы (2.2), проходящие через точки G, замкнуты и целиком лежат в G;
уравнение (2.3) при каждой паре (/г, z) определяет одну и только одну фазовую траекторию системы (2.2), расположенную в G;
на каждой
фазовой траектории (2.3)
системы
(2.2), лежащей
в G,
можно
выбрать по одной точке
,
гладко зависящей от
В самом деле, в силу известных свойств гамильтоновой системы, в пространстве E>2>+i существует некоторая окрестность G траектории (2.4) (Gd G), в которой выполняется условие 1). Выделим из G ту окрестность траектории (2.4), в которой выполняются и условия 2), 3). Для этого возьмем поверхность, пересекающую каждую плоскость z = const области G
о о по нормали в точке (х, у, z) к фазовой траектории системы (2.2), проходящей через эту точку. Уравнение этой поверхности имеет вид:
Следовательно, точка (х, у, z, h) эвклидова пространства £">2>+z переменных х, у, z, h удовлетворяет системе
Левые части системы (2.5) определены и непрерывны вместе со всеми своими частными производными в области Г: (#, у, z) £ G, —ос <^ /г<^оо. Якобиан системы (2.5)
отличен от нуля в точке (х, у, z, /г), так как точка (х,?/, z) не является положением равновесия системы (2.2). Поэтому, по теореме о неявных функциях, в некоторой окрестности Г° точки (х, у, z, h) (Г°С Г) система (2.5) разрешима относительно х и у:
причем
являются однозначными функциями от /г, zi,..., z>x>, непрерывными по совокупности этих переменных вместе со всеми своими первыми частными производными. Следовательно, целые фазовые траектории системы (2.2), проходящие через точки
составляют искомую окрестность G траектории (2.4). Пусть
— решение системы (2.2) с начальными условиями
Решение (2.6) системы (2.2) является периодическим, поскольку описывает замкнутую траекторию (2.3). Тогда, полагая получим:
2. Изучение системы (2.1). Исследуем решение
системы (2.1) с начальными условиями
на конечном промежутке времени Uo, L]. Имеет место
ТЕОРЕМА 1.
Пусть
функции 1
определены
и непрерывны в
вместе со всеми своими частными
произвооными до второго'порядка
включительно, а функции
непрерывны в
вместе со всеми своими первыми частными
производными. Тогда существует число
такое, что при любом
на конечном промежутке времени [to,
L]:
1) решение
системы (2.1)
остается
в G
и функции h
с точностью до величин порядка О (г)
совпадают соответственно с функциями
представляющими собой решение следующей
автономной системы не зависящих от е
обыкновенных
дифференциальных уравнений, правые
части которых выражаются через правые
части системы (2.1):
циал дуги фазовой траектории
(2.3),
интегрирование
ведется при произвольно фиксированной
паре
Предполагаем, что решение системы
(2.8)
имеет начальные значения
2) Функции х (I, е), у (г, е) с точностью до величин порядка О (е) совпадают соответственно с функциями
Здесь ф>0> определяется из соотношений постоянная величина, v (t, e) — решение уравнения:
Доказательство. Прежде всего установим ряд свойств решения (2.6) системы (2.2), имеющих место при тех требованиях гладкости, которые указаны в формулировке теоремы 1.
Свойство
1. Периодом
решения (2.6)
является
функция
следовательно,
эта функция
непрерывна в G>h>
вместе со всеми своими частными
производными до второго порядка
включительно. Действительно,
из (2.2) следует соотношение интегрирование
которого дает формулу (2.9). Из указанной
в условиях теоремы гладкости функций
следует соответствующая гладкость функции Т(h, z) в G>h>.
Свойство 2.
Функции
определены и непрерывны в области —
вместе со всеми своими частными
производными до второго порядка
включительно.
В самом деле,
в силу указанной гладкости правых частей
системы (2.2), из (2.5), по теореме о неявных
функциях, следует, что функции а (/г, z),
Р (/г, z)
непрерывны
в G>h>
вместе со
всеми своими частными производными до
второго порядка включительно. Далее,
из теорем о существовании и единственности,
о непрерывности и непрерывной
дифференцируемости решений системы
обыкновенных дифференциальных уравнений
по начальным значениям и по параметрам
следует, что функции
вместе со всеми своими частными
производными до второго порядка
включительно, непрерывны в области —
.
Следовательно,
функции
обладают свойством 2 как сложные функции.!
Свойство 3.
Пусть D
— некоторая
ограниченная замкнутая об
ласть,
содержащаяся в G>h>.
Тогда на множестве —
функции
вместе со всеми своими частными
производными до второго порядка
включительно ограничены.
Свойство 3
является следствием свойства 2, так как
периодичность функций
позволяет рассматривать их в замкнутой
и ограниченной области
Свойство 4.
так как решение (2.6) описывает фазовую траекторию (2.3). Дифференцирование соотношения (2.10) по Zj дает Свойство 5.
(2.10)
где
(2.11)
Свойство 6.
(2.12)
Свойство 8, Для любой функции y (х, у, z), непрерывной в G, справедливо равенство
где
и интегрирование ведется при произвольно фиксированных
Действительно, вдоль траекторий (2.3), в силу (2.7) и свойства 6, имеем:
что дает:
Перейдем к непосредственному изучению системы (2.1). Заменим переменные х, 2/,%,..., Zi переменными ф, /?, z,,..., z\ по формуле:
что, в силу (2.10), дает:
Преобразование (2.13) — невырожденное в рассматриваемой области поскольку там
(см. свойство 7). В силу (2.12), замена (2.13) переводит систему (2.1) в следующую:
Система (2.14) является линейной алгебраической по отношению к функциям
с определителем
и поэтому она единственным образом разрешима относительно этих функций. По правилу Крамера имеем:
или, в силу свойств 7, 6, 5:
Пусть при
Из последнего соотношения следует:
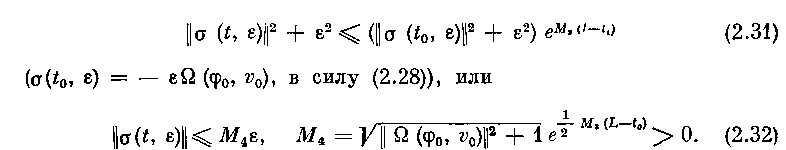
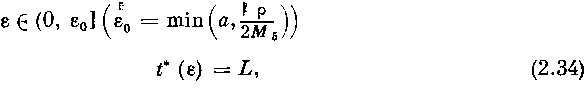
Так как в противном случае
что противоречит определению
Оценим
В силу (2.19), (2.20) и (2.22),
или, по формуле конечных приращений,
(применимость формулы конечных приращений следует из (2.24)). Следовательно, в силу ограниченности функций w (v), В (φ, v, е) и всех их частных производных в области значений, по (2.33), (2.34) имеем:
Поэтому
Из (2.36) следует:
Соотношения (2.33), (2.34), (2.37), (2.38) полностью доказывают теорему об усреднении (м° = max (М>5>, М>в>), е>0> = min(a,^)).
Вернемся к доказательству теоремы 1. Так как система (2.15) типа (2.19), то, по теореме об усреднении, существует число е>0> > 0 такое, что при любых eg (0, е>0>], t 6 [*<>> L] решение {ф (t, е), h (t, е), z (t, г)} системы (2.15) с начальными условиями
и решение {ф (t, e), h(t), z (t)} усредненной системы (2.17) с теми же начальными условиями
связаны следующим образом: точка {h (t, e), z (t, г)} остается в некоторой и выполняются соотношения:
окрестность решения)). А так как, по (2.13),
и так как точка {h (£, е), z (t, е)} остается в G>hp> CZ G>h>, то на отрезке [t>Q>, L] при любом 8 g (0, е>0>] решение {х (t, е),?/ (£, е), z (£, г)} системы (2.1) остается в G, причем, по свойству 3,
В силу же (2.13),
и потому соотношения (2.39), (2.40) доказывают первую часть теоремы 1. Докажем вторую часть теоремы 1. По формуле конечных приращений, из (2.41) получаем:
Возникает вопрос, как ведут себя решения системы (2.1) во всей указанной окрестности Go (включая и положения равновесия {/ (z), g (z), z} системы (2.3)). На этот вопрос отвечают теорема 1 и нижеследующие теоремы 2 и 3.
ТЕОРЕМА 2. Пусть в окрестности Go выполнены условия теоремы 1, касающиеся гладкости правых частей системы (2.1). Тогда найдется число 8° у> О, такое, что при любом г £ (0, е°] (е° <^ а) на конечном промежутке времени [to,L] решение {х (t, е), у (t, е), z (t, г)} системы (2.1) с начальными условиями вырожденной системы
остается в Go и с точностью до величин порядка О (г) совпадает с решением
проходящим при t — to через то же положение равновесия
(предполагается, что решение {х (t), у (t), z (t)} остается в G на [t>0>, L]). Доказательство. Не нарушая общности рассуждений, будем считать, что в Go
1 1 так как замена переменных х, у, z>x>,..., z>t> на х, у, z>1?>.... z> и Н
на Я1, где
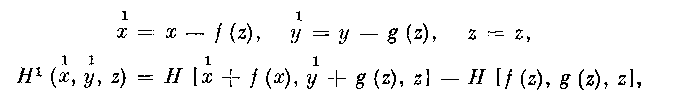
сохраняет вид системы (2.1), но дает условия (2.54). Следовательно, в силу.
Это решение на конечном промежутке времени [t>0>, L] составляет некоторое замкнутое ограниченное множество F>Q> CZ G>0> и поэтому найдется ро > 0 такое, что G>00> С G>0> (G>Q>>0> — р>0>-окрестность F>0>).
Положим
В силу (2.56) и (2.1), вдоль решения {х (£, е), у (t, е), z (t, &)} имеем:
Следовательно, по формуле Тейлора, примененной к функциям
относительно х, у в G>00>, в силу (2.54), (2.58), получим на [t>0>, t^ (г)]:
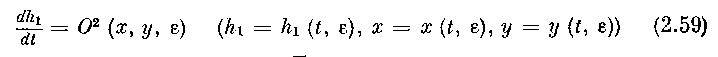
(формула Тейлора применима в G>00> относительно х, у, так как прямолинейный отрезок, соединяющий любые две точки (я, у, z) и (0, 0, z) из Goo, содержится в Goo, поскольку каждое сечение области G>00> плоскостью z = const представляет собой круг с центром в точке (0, 0, z), по определению Goo).
Функция О2 (х, у, е), в силу указанной в условиях теоремы гладкости правых частей системы (2.1), является однородной квадратичной относительно х, у, е с ограниченными в Goo коэффициентами, и поэтому
постоянная величина).
С другой стороны, по формуле Тейлора, в силу (2.54) имеем в G>00>
и так как при (х, у, z)
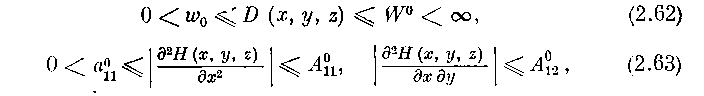
то соотношение (2.61), в силу (2.57), дает на [£>0>, t(е)]:
Но, по (2.56) - (2.58) и (2.63),
Соотношения
дают:
откуда следует, что на отрезке
Но так как, в силу
т. е. окончательно, по (2.64), (2.67),
2. Регулярные возмущения.
2.1 Асимптотические методы
Пусть задано
банахово пространство
и отображение
.
Определение.
Будем ряд
называть асимптотическим
рядом
для функции
,
если для любого
найдутся числа
и
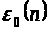такие, что
при
(2.1)
Пример 1.
Если функция
имеет производные всех порядков в точке
,
то справедливо формула Тейлора
(2.2)
Ряд Тейлора
может расходиться на любом отрезке
,
но он будет асимптотическим рядом для
функции
.
Действительно,
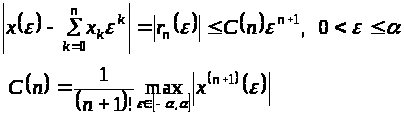(2.3)
Пример 2. Рассмотрим функцию
Интегрируя по частям, получаем
Таким образом,
Ряд
расходится при любом
,
но является асимптотическим для функции
,
так как
Замечание. Асимптотический ряд может быть полезен при вычислении значений функции при малых или больших значениях параметра.
Рассмотрим
функцию примера 2. Вычисляя интеграл
численно, получаем при
Вычисляя
частичные суммы асимптотического ряда
и оценивая разности
,
получаем первые 20 чисел
0.0015633, -0.0004366, 0.0001633, -0.0000766, 0.0000433, -0.0000287, 0.0000217,
-0.000186, 0.0000177, -0.0000186, 0.00002133, -0.0000266, 0.0000357, -0.0000515,
0.0000793, -0.0001299, 0.0002257, -0.0004145, 0.0008020
Наилучшее приближение дает девятая частичная сумма.
На рис. 1
изображен графически характер приближения
частичных сумм к значению.
На горизонтали оси откладывается номер
,
по вертикали частичная сумма
.
рис. 1
Пусть
банаховы
пространства
и при
задано семейство операторов
.
Рассмотрим при
уравнение
.
Допустим, что это уравнение при каждом
имеет единственное решение
.
Уравнение
будем называть вырожденным.
Допустим, что вырожденное уравнение
имеет единственное решение
.
Будем говорить, что вырождение регулярное,
если
при
(2.4)
Если (18.4) не выполняется, то говорят, что вырождение сингулярное.
Распространена
еще и такая терминология: Уравнение
называют уравнением
возмущений для
уравнения
.
Если условие (2.4) выполнено, то говорят
о регулярных
возмущениях. В противном случае речь
идет о сингулярных
возмущениях. Сам термин «теория
возмущений» возник в рамках небесной
механики. В следующем параграфе будет
исследована задача о регулярных
возмущениях для обыкновенных
дифференциальных уравнений.
2.2 Регулярные возмущения решений задачи Коши для обыкновенных дифференциальных уравнений
Рассмотрим
задачу Коши
(2.2.1)
Функция
непрерывна по переменной
и бесконечно дифференцируемая по
переменным
и
при
,
, 
.
Предполагается,
что вырожденная задача
(2.2.2)
имеет
единственное решение при
,
причем
.
Полагая
(2.2.3)
и воспользовавшись
тем, что функция
удовлетворяет
уравнению (2.2.2) запишем систему уравнений
для функции
в виде
(2.2.4)
где
(2.2.5)
(2.2.6)
Будем искать
решение задачи Коши (2.1.4) в виде формального
ряда по степеням малого параметра
(2.2.7)
Для определения
неизвестных функций
получаем рекуррентную систему задач
Коши для линейных уравнений (уравнений
в вариациях)
(2.2.8)
Уравнение (2.2.8) называют уравнением в вариациях.
Вычислим две
первых функции
(2.2.9)
Подставляя разложения (2.2.7) и (2.2.8) в уравнения (2.2.4),получаем рекуррентную систему уравнений
(2.2.10)
Все уравнения (2.2.4) имеют одинаковую структуру
,
(2.1.11)
Столбцы
фундаментальной
матрицы
образуют фундаментальную систему
решений. При помощи формулы
Коши получим
решение в виде
(2.2.12)
Линейный
оператор 
(2.2.13)
Покажем, что
ряд (2.2.3) асимптотический для решения
.
Положим
(2.2.14)
Применяя формулу Тейлора, получаем
(2.2.15)
где функции
те же, что и в формуле (19.8), а
(2.2.16)
Подставляя
представление (2.2.14) в уравнение (2.2.4),
воспользовавшись представлением
(2.2.15) и формулами (2.2.8), получаем уравнение
для функции
.
(2.2.17)
где
(2.2.18)
Из формулы (2.2.6) получаем
и формула (2.2.18) может быть записана в виде
(2.2.19)
Так как вторые
производные функции
ограничены, то функция
удовлетворяет условию Липшица и
(2.2.20)
Вспоминая
определение оператора
,
получаем функциональное уравнение
(2.2.21)
Используя
принцип сжатых отображений, покажем,
что уравнение (2.1.21) при
имеет единственное решение, и справедливо
неравенство
.
Тем самым будет доказано, что ряд
является асимптотическим рядом для
функции
,
являющейся решением задачи Коши (2.2.1).
Пусть
.
Так как частные производные равномерно
непрерывны, то из (2.2.17)- (2.2.20) получаем
оценки
при
.
Таким образом, шар радиуса
отображается в себя при.
Используя (2.2.20), получаем
Используя равномерную непрерывность частных производных, получаем
Уменьшая,
если нужно,
получаем, что при
оператор
является оператором сжатия. Следовательно,
и ряд
асимптотический
для решения
задачи Коши (2.1.1).
2.3 Существование решении возмущенной задачи
Результаты, полученные обладают той особенностью, что справедливость асимптотического представления гарантируется на некотором сегменте [0,T], определяемом свойствами правой части (2.3.1), одновременно с существованием и единственностью как невозмущенного, так и возмущенного уравнений.
Можно ставить вопрос иначе. Допустим, что решение невозмущенной задачи (2.3.2) существует, единственно и принадлежит некоторой области G пространства переменных y(t,μ) при, 0≤t≤T. Величину T в данном случае можно, например, установить непосредственно из явного вида y(t). Будет ли при достаточно малых μ решение задачи (2.3.1) также существовать на всем [0,T] и подчиниться формуле (1.3)? Ответ на этот вопрос дает следующая
Теорема 1.2. Пусть в области
непрерывны и равномерно
ограничены:
Пусть решение
y(t)
задачи
(2.3.2)
существует,
единственно на [0,T]
и
принадлежит
.
Тогда при каждом достаточно малом μ
решение y(t,μ)
задачи
(2.3.1) также
существует, единственно на [0,T]
принадлежит
G,
и имеет место равномерный относительно
предельный
переход
(2.3.8)
Доказательство.
Перейдем в (2.3.1) к новой неизвестной
функции
.
Имеем
Перейдем к эквивалентному интегральному уравнению
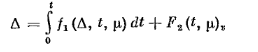(2.3.9)
где
причем
.
Здесь и в
дальнейшем бесконечно малые при μ →0 величины будем обозначать
ω(μ), ω>1>(μ)
и т. д. Применим к уравнению (2.3.9) метод
последовательных приближений и докажем,
что ▲(t,μ)
существует
на сегменте [0,Т] и
.Это
очевидно, равносильно утверждению
теоремы 1.2.
Построим последовательные приближения обычным образом
Предварительно
заметим, что так как y=y(t)
принадлежит G
для
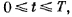кривая
,
где
при
достаточно малом μ. также принадлежит
G
для
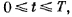
Положим
Тогда
(2.3.10)
|
В равномерной
сходимости последовательности (k)▲
к решению
▲(t,μ)
уравнения
(2.3.9) можно убедиться совершенно, может
в пределе при k→∞
появиться равенство. Поэтому
,
что равносильно (2.3.8).
Замечание. Теорема доказана для скалярного случая, но аналогичное утверждение справедливо и для случая, когда y — вектор.
2.3.2 Теорема 2.3.2 остается справедливой, если имеет место возмущение не только в уравнении, во и в начальных условиях, т. е. имеет вид
Литература
Понтрягин Л.С. Асимптотическое поведение решений системы дифференциальных уравнений с малым параметром при высших производных, Известия Ак. паук СССР, серия метем, 21(1957), 605—626.
Мищенко Е.Ф., Понтрягии Л.С. Периодические решения систем дифференциальных уравнении, близкие к разрывным, Доклады Ак. наук СССР, 102, № 5 (1955), 889-891.
Мищенко Е.Ф., Асимптотическое вычисление периодических решении систем дифференциальных уравнении, содержащих малые параметры при производные. Известия Ак. наук СССР, серия матем., 21 (1957), 627—654.
Мищенко Е., Понтрягии Л.С. Вывод некоторых асимптотических оценок для решений дифференциальных уравнений с малым параметром пр" производных, Известия Ак. наук СССР, серия матем., 23(1959), 643—660.
Тихонов А. И-, Системы дифференциальных уравнений, содержащие малые параметры при производных, Матем. еборн., 31(73): 3 (1952), 574—586.
Боголюбов Н.И., Митропольский Ю.А., Асимптотические методы в теории нелинейных колебаний, Москва, 1955.
Митропольскнй Ю.А., Нестационарные процессы в нелинейных колебательных системах, Изд. АН УССР, 1955.