*-Алгебры и их применение
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ТАВРИЧЕСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
им. В.И. ВЕРНАДСКОГО
ФАКУЛЬТЕТ МАТЕМАТИКИ И ИНФОРМАТИКИ
КАФЕДРА АЛГЕБРЫ И ФУНКЦИОНАЛЬНОГО АНАЛИЗА
*-АЛГЕБРЫ И ИХ ПРИМЕНЕНИЕ
Дипломная работа специалиста
|
студент 5 курса специальности математика _________________________________ НАУЧНЫЕ РУКОВОДИТЕЛИ: ассистент каф. алгебры и функционального анализа _________________________________ профессор, доктор физико-математических наук _________________________________ РЕШЕНИЕ О ДОПУСКЕ К ЗАЩИТЕ: зав. кафедрой, профессор, д.ф.м.н. _________________________________ |
СИМФЕРОПОЛЬ
2003
СОДЕРЖАНИЕ
Введение……………………………………………………………………………..4
Глава I. Основные понятия и определения…………………………………….6
§ 1. * - алгебры……………………………………………………………………...6
1.1. Определение * - алгебры……………………………………………………….6
1.2. Примеры…………………………………………………………………………7
1.3. Алгебры с единицей…………………………………………………………….7
1.4. Простейшие свойства * - алгебр……………………………………………….9
1.5. Гомоморфизм и изоморфизм алгебр…………………………………………11
§ 2. Представления ……………………………………………………………….13
2.1. Определение и простейшие свойства представлений……………………….13
2.2. Прямая сумма представлений ………………………………………………..15
2.3. Неприводимые представления………………………………………………..16
2.4. Конечномерные представления……………………………………………….19
2.5. Интегрирование и дезинтегрирование представлений ……………………..20
§ 3. Тензорные произведения……………………………………………………26
3.1. Тензорные произведения пространств……………………………………….26
3.2. Тензорные произведения операторов………………………………………..28
Глава II. Задача о двух ортопроекторах………………………………………..31
§ 1. Два ортопроектора в унитарном пространстве…………………………..31
1.1. Постановка задачи……………………………………………………………..31
1.2. Одномерные *-представления *-алгебры P>2> ……………………………….31
1.3. Двумерные *-представления *-алгебры P>2> ……………………………….32
1.4. n-мерные *-представления *-алгебры P>2> …………………………………35
1.5. Спектральная теорема…………………………………………………………37
§ 2. Два ортопроектора в сепарабельном гильбертовом пространстве……39
2.1. Неприводимые *-представления *-алгебры P>2> …………………………...39
2.2. Спектральная теорема…………………………………………………………41
Глава III. Спектр суммы двух ортопроекторов ……………………………...45
§ 1. Спектр суммы двух ортопроекторов в унитарном пространстве……...45
1.1. Спектр ортопроектора в гильбертовом пространстве……………………….45
1.2. Постановка задачи……………………………………………………………..45
1.3. Спектр в одномерном пространстве………………………………………….45
1.4. Спектр в двумерном пространстве……………………………………….…..46
1.5. Спектр в n-мерном пространстве……………………………………………..47
1.6. Линейная комбинация ортопроекторов………………………………………49
§ 2. Спектр суммы двух ортопроекторов в сепарабельном
гильбертовом пространстве …………………………………………………….52
2.1. Спектр оператора А = Р>1> +Р>2> …………………………………………………52
2.2. Спектр линейной комбинации А = аР>1> + bР>2> (0<а<b) ……………………..53
Заключение………………………………………………………………………..55
Литература ………………………………………………………………………..56
ВВЕДЕНИЕ
Пусть Н – гильбертово пространство, L(Н) – множество непрерывных линейных операторов в Н. Рассмотрим подмножество А в L(Н), сохраняющееся при сложении, умножении, умножении на скаляры и сопряжении. Тогда А – операторная *-алгебра. Если дана абстрактная *-алгебра А, то одна из основных задач теории линейных представлений (*-гомоморфизмов А в L(Н)) – перечислить все ее неприводимые представления (с точностью до эквивалентности).
Теория унитарных представлений групп восходит к XIX веку и связана с именами Г.Фробениуса, И.Шура, В.Бернсайда, Ф.Э. Молина и др. В связи с предложениями к квантовой физике теория унитарных представлений топологических групп, групп Ли, С*-алгебр была разработана И.М.Гельфандом, М.А. Наймарком, И.Сигалом, Ж.Диксмье, А.А. Кирилловым и др. в 60-70-х годах XX века. В дальнейшем интенсивно развивается теория представлений *-алгебр, заданных образующими и соотношениями.
Дипломная работа посвящена развитию теории представлений (конечномерных и бесконечномерных) *-алгебр, порожденных двумя проекторами.
Глава I в краткой форме содержит необходимые для дальнейшего сведения из теории представлений и функционального анализа. В §1 дано определение *-алгебры и приведены простейшие свойства этих алгебр. В §2 излагаются основные свойства представлений, вводятся следующие понятия: неприводимость, эквивалентность, прямая сумма, интегрирование и дезинтегрирование представлений. В §3 определяются тензорные произведения пространств, тензорные произведения операторов и др. (см. [2], [3], [4], [8], [9])
В Главе II изучаются представления *-алгебры P>2>
P>2>> >= С < p>1>, p>2> | p>1>2 = p>1>* = p>1>, p>2>2 = p>2>* = p>2> >,
порожденной двумя самосопряженными идемпотентами, то есть проекторами (см., например, [12]). Найдены все неприводимые *-представления *-алгебры P>2>, с точностью до эквивалентности., доказаны соответствующие спектральные теоремы.
В §1 рассматриваются только конечномерные *-представления π в унитарном пространстве Н. Описаны все неприводимые и неэквивалентные *-представления *-алгебры P>2> . Неприводимые *-представления P>2> одномерны и двумерны:
4 одномерных: π>0,0>(p>1>) = 0, π>0,0>(p>2>) = 0; π>0,1>(p>1>) = 0, π>0,1>(p>2>) = 1;
π>1,0>(p>1>) = 1, π>1,0>(p>2>) = 0; π>1,1>(p>1>) = 1, π>1,1>(p>2>) = 1.
И двумерные:
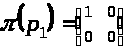 ,
,
 τ
τ
 (0, 1).
(0, 1).
Доказана спектральная теорема о разложении пространства Н в ортогональную сумму инвариантных относительно π подпространств Н, а также получено разложение π на неприводимые *-представления. Результаты §1 относятся к математическому фольклору.
В §2 получены основные результаты работы. Для пары проекторов в сепарабельном гильбертовом пространстве Н приведено описание всех неприводимых представлений, доказана спектральная теорема.
В Главе III спектральная теорема для пары проекторов Р>1, >Р>2>, применяется к изучению сумм Р>1>+Р>2>, аР>1>+bР>2> (0 < a < b). Получены необходимое и достаточное условие на самосопряженный оператор А для того чтобы А = Р>1>+Р>2>> >или А = аР>1>+bР>2>, 0 < a < b, (этот частный случай задачи Г.Вейля (1912 г.) о спектре суммы пары самосопряженных операторов).

Глава I. Основные понятия и определения
§ 1.
 -
алгебры
-
алгебры
Определение
 -
алгебры.
-
алгебры.
Определение 1.1.
Совокупность А
элементов x,
y,
… называется алгеб-
рой, если:
А есть линейное пространство;
в А
введена операция умножения (вообще
некоммутативного), удовлет-
воряющая
следующим условиям:
α (x y) = (α x) y,
x (α y) = α (x y),
(x y) z = x (y z),
(x + y) = xz +xy,
x
(y
+ z)
= xy
+ xz
для любых x,
y,
z
 А и любых чисел
α.
А и любых чисел
α.
Два элемента x,
y
алгебры А
называются перестановочными, если xy
= yx.
Алгебра А
называется коммутативной, если все ее
элементы попарно пере-
становочны.
Определение 1.2. Пусть А – алгебра над полем С комплексных чисел. Инволюцией в А называется такое отображение x → x* алгебры А в А, что
(x*)* = x;
(x + y)* = x* + y*;
(α
x)* =
 x*;
x*;
(x
y)*
= y*x*
для любых x,
y
 С.
С.
Алгебра над С, снабженная
инволюцией, называется инволютивной
алгеброй или *- алгеброй. Элемент х*
называют сопряженным к х. Подмножество
А, сохраняющееся при инволюции,
называется само-
сопряженным.
Из свойства (i) следует, что инволюция в А необходимо является биекцией А на А.
1.2. Примеры
На А
= С отображение
z
→ (комплексное число, сопряженное к z)
есть инволюция, превращающая С
в коммутативную *- алгебру.
(комплексное число, сопряженное к z)
есть инволюция, превращающая С
в коммутативную *- алгебру.
Пусть Т
– локально компактное пространство,
А = С(Т)
– алгебра непре-
рывных комплексных
функций на Т,
стремящихся к нулю на бесконечности
(то есть для любого ε > 0
множество {t T:
|f
(t)|
T:
|f
(t)|
 ε} компактно, f
(t)
ε} компактно, f
(t)
 А. Снабжая А
отображением f→
А. Снабжая А
отображением f→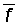 получаем коммутативную *- алгебру. Если
Т сводится к
одной точке, то возвращаемся к примеру
1).
получаем коммутативную *- алгебру. Если
Т сводится к
одной точке, то возвращаемся к примеру
1).
Пусть Н – гильбертово пространство. А = L(H) – алгебра ограниченных линейных операторов в Н. Зададим инволюцию как переход к сопряженному оператору. Тогда А - *- алгебра.
Обозначим через К(Н)
совокупность всех компактных операторов
в гильбертовом пространстве Н;
операции сложения, умножения на число
и умножения определим как соответствующие
действия с операторами. Тогда К(Н)
будет *- алгеброй, если ввести инволюцию
А→А*
(А К(Н)).
Алгебра К(Н)
в случае бесконечного Н
есть алгебра без единицы. Действительно,
если единичный оператор I
принадлежит К(Н),
то он переводит открытый единичный шар
S
К(Н)).
Алгебра К(Н)
в случае бесконечного Н
есть алгебра без единицы. Действительно,
если единичный оператор I
принадлежит К(Н),
то он переводит открытый единичный шар
S H
в себя. Значит I
не может быть компактным оператором.
H
в себя. Значит I
не может быть компактным оператором.
Обозначим через W
совокупность всех абсолютно сходящихся
рядов
 .
.
Алгебра W
есть *- алгебра, если положить
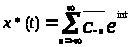 .
(
.
( )
)
1.3. Алгебры с единицей
Определение 1.3. Алгебра А называется алгеброй с единицей, если А содержит элемент е, удовлетворяющий условию
ех = хе = х для
всех х А
(1.1.)
А
(1.1.)
Элемент е называют единицей алгебры А.
Теорема 1.1. Алгебра А не может иметь больше одной единицы.
Доказательство. Действительно, если е΄ - также единица в А, то
е΄х = хе΄ = х, для
всех х А
(1.2.)
А
(1.2.)
Полагая в (1.1.) х = е΄, а в (1.2.) х = е, получим:
ее΄ = е΄е = е΄ и е΄е = ее΄ =е, следовательно е΄ = е.
Теорема 1.2. Всякую алгебру А без единицы можно рассматривать как подалгебру некоторой алгебры А΄ с единицей.
Д оказательство.
Искомая алгебра должна содержать все
суммы х΄=αе + х,
х
оказательство.
Искомая алгебра должна содержать все
суммы х΄=αе + х,
х А;
с другой стороны, совокупность всех
таких сумм образует алгебру А΄,
в которой основные операции определяются
формулами:
А;
с другой стороны, совокупность всех
таких сумм образует алгебру А΄,
в которой основные операции определяются
формулами:
β(αе + х) = βαе + βх, (α>1>е + х>1>) + (α>2>е + х>2>) = (α>1> + α>2>)е + (х>1> + х>2>),
(α>1 >е + х>1>)(α>2 >е+ х>2> )=α>1> α>2 >е +α>1 >х>2> +α>2 >х>1> + х>1> х>2 > (1.3.)
Каждый элемент х΄ из А΄ представляется единственным образом в виде
х΄ = αе + х, х А,
так как по условию А
не содержит единицы. Поэтому А΄
можно реализовать как совокупность
всех формальных сумм х΄ =
αе + х, х
А,
так как по условию А
не содержит единицы. Поэтому А΄
можно реализовать как совокупность
всех формальных сумм х΄ =
αе + х, х А,
в которой основные операции определяются
формулами (1.3.); сама алгебра А
получится при α = 0.
А,
в которой основные операции определяются
формулами (1.3.); сама алгебра А
получится при α = 0.
А лгебру
А΄ можно также
реализовать как совокупность всех пар
(α, х), х
лгебру
А΄ можно также
реализовать как совокупность всех пар
(α, х), х А,
в которой основные операции определяются
по формулам:
А,
в которой основные операции определяются
по формулам:
β (α, х) = (βα, βх), (α>1>,> >х>1>) + (α>2>, х>2>) = (α>1> + α>2>, х>1> + х>2>),
(α>1>,> >х>1>)(α>2>, х>2>) = (α>1>α>2>, α>1>х>2> + α>2> х>1> + х>1>х>2>), (1.4.)
аналогично тому, как определяются
комплексные числа. Саму алгебру А
можно тогда рассматривать как совокупность
всех пар (0, х), х А
и не делать различия между
х и (0,
х). Полагая е
= (0, х), мы получим:
А
и не делать различия между
х и (0,
х). Полагая е
= (0, х), мы получим:
(α, х) = α(1, 0) + (0, х) = αе + х,
так что вторая реализация алгебры А΄ равносильна первой.
Переход от А к А΄ называется присоединением единицы.
Определение 1.4. Элемент y называется левым обратным элемента х, если xy = e. Элемент z называется правым обратным элемента х, если xz = e.
Если элемент х имеет и левый, и правый обратные, то все левые и правые обратные элемента х совпадают. Действительно, умножая обе части равенства yx = e справа на z, получим
z = (yx)z = y(xz) = ye,
В этом случае говорят, что существует обратный х-1 элемента х.
1.4. Простейшие свойства
 -
алгебр
-
алгебр
Определение 1.5. Элемент х *-алгебры А называется эрмитовым или самосопряженным, если х* = х, нормальным, если хх* = х*х. Идемпотентный эрмитов элемент называется проектором. Элемент алгебры называется идемпотентным, если все его (натуральные) степени совпадают.
Каждый эрмитов элемент нормален.
Множество эрмитовых элементов есть
вещественное векторное подпространство
А. Если х
и y
эрмитовы, то (xy)*=
y*x*
= yx;
следовательно, xy
эрмитов, если x
и y
перестановочны. Для каждого х А
элементы хх*
и х*х эрмитовы.
Но, вообще говоря, эрмитов элемент не
всегда представим в этом виде, как
показывает пример 1 из пункта 1.2.
Действительно, для любого z
А
элементы хх*
и х*х эрмитовы.
Но, вообще говоря, эрмитов элемент не
всегда представим в этом виде, как
показывает пример 1 из пункта 1.2.
Действительно, для любого z C
C
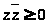 ,
но если z
действительно отрицательное число, то
его нельзя представить в виде
,
но если z
действительно отрицательное число, то
его нельзя представить в виде
 .
.
Теорема 1.3. Всякий элемент х *-алгебры А можно представить, и притом единственным образом, в виде х = х>1> +iх>2>, где х>1>, х>2> – эрмитовы элементы.
Доказательство. Если такое представление имеет место, то х* = х>1> +iх>2>, следовательно:
 ,
,
 (1.5.)
(1.5.)
Таким образом, это представление единственно. Обратно, элементы х>1>, х>2>, определенные равенством (1.5.), эрмитовы и х = х>1> +iх>2>.
Эти элементы х>1>, х>2> называются эрмитовыми компонентами элемента х.
Заметим, что хх* = х>1>2 + х>2>2 + i(х>2>х>1> – х>1>х>2>),
хх* = х>1>2 + х22 - i(х>2>х1 – х1х2)
так что х нормален тогда и только тогда, когда х>1> и х>2> перестановочны.
Так как е*е = е* есть эрмитов элемент, то е* = е , то есть единица эрмитов элемент.
Если А -
*-алгебра без единицы, а А΄
- алгебра, полученная из А
присоединением единицы,
то, положив
 при х
при х А,
мы определим инволюцию в А΄,
удовлетворяющую всем требованиям
определения 2. Так что А΄
станет *-алгеброй. Говорят, что А΄
есть *-алгебра, полученная из А
присоединением единицы.
А,
мы определим инволюцию в А΄,
удовлетворяющую всем требованиям
определения 2. Так что А΄
станет *-алгеброй. Говорят, что А΄
есть *-алгебра, полученная из А
присоединением единицы.
Теорема 1.4. Если х-1 существует, то (х*)-1 также существует и
(х*)-1 = (х-1)*
Доказательство. Применяя операцию * к обеим частям соотношения
х-1х = хх-1 = е,
получим х*(х-1)*= (х*)-1х*=е.
Но это означает, что (х-1)* есть обратный к х*.
Подалгебра А>1>
алгебры А
называется *-подалгеброй,
если из х А>1>
следует, что х*
А>1>
следует, что х* А>1>
.
А>1>
.
Непустое пересечение *-подалгебр
есть также *-подалгебра. В частности,
пересечение всех *-поалгебр, содержащих
данное множество S А, есть минимальная
*-подалгебра, содержащая S.
А, есть минимальная
*-подалгебра, содержащая S.
Коммутативная *-алгебра называется максимальной, если она не содержится ни в какой другой коммутативной *-подалгебре.
Теорема 1.5. Если
В – максимальная
коммутативная *-подалгебра, содержащая
нормальный элемент х
, и если х-1
существует, то х-1 В.
В.
Доказательство. Так как х
т х* перестановочны
со всеми элементами из В,
то этим же свойством обладают х-1
и (х*)-1
= (х-1)*.
В силу максимальности В
отсюда следует, что х-1 В.
В.
Определение 1.6.
Элемент х А
- *-алгебры называется
унитарным, если хх* = х*х =
е, иначе говоря, если х
обратим и х = (х*)-1.
А
- *-алгебры называется
унитарным, если хх* = х*х =
е, иначе говоря, если х
обратим и х = (х*)-1.
В примере 1 п.1.2. унитарные элементы – комплексные числа с модулем, равным 1.
Унитарные элементы А образуют группу по умножению – унитарную группу А. Действительно, если x и y – унитарные элементы *-алгебры А, то
((хy)*)-1 = (у*х*)-1 =(х*)-1 (y*)-1 = xy,
поэтому xy унитарен, и так как ((х-1)*)-1= ((х*)-1)-1 = х-1, то х-1 унитарен.
1.5. Гомоморфизм и изоморфизм алгебр
Определение 1.7. Пусть А и В – две *-алгебры. Назовем гомоморфизмом (*-гомоморфизмом) А в В такое отображение f множества А в В, что
f (x + y) = f (x) + f (y),
f (αx) = α f (x),
f (xy) = f (x) f (y),
f (x*) = f (x)*
для любых х,y А,
α
А,
α С.
Если отображение f
биективно, то f
называют изоморфизмом (*-изоморфизмом).
С.
Если отображение f
биективно, то f
называют изоморфизмом (*-изоморфизмом).
Определение 1.8. Совокупность I элементов алгебры А называется левым идеалом, если:
I ≠ A;
Из х, y I
следует x
+ y
I
следует x
+ y
 I;
I;
Из х I,
а α
I,
а α А
следует α
х
А
следует α
х I.
I.
Если I = А, то I называют несобственным идеалом.
Аналогично определяется и правый идеал. Идеал, являющийся одновременно и левым, и правым, называется двусторонним.
Всякий идеал автоматически оказывается алгеброй.
Пусть I
– двусторонний идеал в алгебре А.
Два элемента х, y
из А назовем
эквивалентными относительно идеала I,
если х-y I.
Тогда вся алгебра А
разбивается на классы эквивалентных
между собой элементов. Обозначим через
А совокупность
всех этих классов. Введем в А>1>
операции сложения, умножения на число
и умножения, производя эти действия над
представителями классов. Так как I
– двусторонний идеал, то результат
операций не зависит от выбора этих
представителей.
I.
Тогда вся алгебра А
разбивается на классы эквивалентных
между собой элементов. Обозначим через
А совокупность
всех этих классов. Введем в А>1>
операции сложения, умножения на число
и умножения, производя эти действия над
представителями классов. Так как I
– двусторонний идеал, то результат
операций не зависит от выбора этих
представителей.
Следовательно, А>1 > становится алгеброй. Эта алгебра называется фактор-алгеброй алгебры А по идеалу I и обозначается A/I.
*-гомоморфизм алгебр описывается при помощи так называемых самосопряженных двусторонних идеалов.
Определение 1.9.
Идеал I
(левый, правый или двусторонний) называется
самосопряженным, если из х I
следует х*
I
следует х* I.
I.
Самосопряженный идеал автоматически является двусторонним. Действительно, отображение х → х* переводит левый идеал в правый и правый идеал в левый; если поэтому отображение х → х* переводит I в I, то I есть одновременно и левый и правый идеал.
В фактор-алгебре A/I
по самосопряженному
двустороннему идеалу I
можно определить инволюцию
следующим образом. Если х-y I,
то х*-y*
I,
то х*-y* I.
Поэтому при переходе от х
к х* каждый
класс вычетов х
по идеалу I
переходит в некоторый другой класс
вычетов по I.
Все условия из определения 1.2. выполнены;
следовательно, A/I
есть *-алгебра.
I.
Поэтому при переходе от х
к х* каждый
класс вычетов х
по идеалу I
переходит в некоторый другой класс
вычетов по I.
Все условия из определения 1.2. выполнены;
следовательно, A/I
есть *-алгебра.
Если х → х΄ есть *-гомоморфизм А на А΄, то полный прообраз I нуля (то есть ядро данного гомоморфизма) есть самосопряженный двусторонний идеал в А. Фактор-алгебра A/I *-изоморфна *-алгебре А΄.
Обратно, отображение х
→ [х] каждого элемента х А
в содержащий его класс
вычетов по I
есть *-гомоморфизм алгебра А
на A/I.
А
в содержащий его класс
вычетов по I
есть *-гомоморфизм алгебра А
на A/I.
§ 2. Представления
2.1. Определения и простейшие свойства представлений.
Определение 2.1. Пусть А - *-алгебра, Н – гильбертово пространство. Представлением А в Н называется *-гомоморфизм *-алгебры А в *-алгебру ограниченных линейных операторов L(H).
Иначе говоря, представление *-алгебры А в Н есть такое отображение из А в L(H), что
π (x+y) = π (x) + π (y), π (α x) = α π(x),
π (xy) = π (x) π (y), π (x*) = π (x)*
для любых х, y
 А и α
А и α
 С.
С.
Размерность гильбертова пространства Н называется размеренностью π и обозначается dimπ. Пространство Н называется пространством представления π.
Определение 2.2.
Два представления π>1>
и π>2>
инволютивной алгебры А
в Н>1>
и Н>2>
соответственно, эквивалентны
(или унитарно эквивалентны), если
существует унитарный оператор U,
действующий из гильбертова пространства
Н>1>
в гильбертово пространство Н>2>,
переводящий π>1>(х)
в π>2>(х)
для любого х А,
то есть
А,
то есть
U π>1>(х) =
π>2>(х) U для
всех х
 А.
А.
Определение
2.3. Представление π
называется циклическим, если в пространстве
Н
существует вектор f
такой, что множество всех векторов π
(х)f
(для всех х А)
плотно в Н.
Вектор f
называют циклическим (или тотализирующим)
для представления π.
А)
плотно в Н.
Вектор f
называют циклическим (или тотализирующим)
для представления π.
Определение 2.4.
Подпространство Н>1> Н
называется инвариантным,
относительно представления π,
если π (А)Н>1>
Н
называется инвариантным,
относительно представления π,
если π (А)Н>1> Н>1>.
Н>1>.
Если Н>1>
инвариантное подпространство,
то все операторы π(х)
(х А)
можно рассматривать как операторы Н>1>.
Сужения π(х)
на Н>1>
определяют подпредставления π>1>
*-алгебры А
в Н>1>.
А)
можно рассматривать как операторы Н>1>.
Сужения π(х)
на Н>1>
определяют подпредставления π>1>
*-алгебры А
в Н>1>.
Теорема 2.1. Если Н>1> инвариантное подпространство Н, то его ортогональное дополнение также инвариантно.
Доказательство. Пусть f
ортогонален к Н>1>,
то есть (f,
g)
= 0 для всех g Н>1>.
Тогда для любого х
Н>1>.
Тогда для любого х А
(π(х)f,
g)
= (f,
π(х)*g)
= (f, π(х*)g)
= 0,
так как π(х*)g
А
(π(х)f,
g)
= (f,
π(х)*g)
= (f, π(х*)g)
= 0,
так как π(х*)g Н>1>.
Следовательно, вектор π(х)f
также ортогонален к Н>1>.
Н>1>.
Следовательно, вектор π(х)f
также ортогонален к Н>1>.
Обозначим через Р>1>
оператор проектирования в Н
на подпространство Н>1> Н>1>.
Н>1>.
Теорема 2.2. Н>1> – инвариантное подпространство тогда и только тогда, когда все операторы представления перестановочны с оператором проектирования Р>1> на Н>1>.
Доказательство. Пусть Н>1>
– инвариантное подпространство и f Н>1>,
но также π(х)f
Н>1>,
но также π(х)f
 Н>1>.
Отсюда для любого вектора f
Н>1>.
Отсюда для любого вектора f Н
Н
π(х)Р>1>f
 Н>1>
Н>1>
следовательно, Р>1>π(х)Р>1>f = π(х)Р>1>f ,
то есть Р>1>π(х)Р>1> = π(х)Р>1>.
Применяя операцию инволюции к обеим частям этого равенства и подставляя затем х* вместо х, получаем, что также
Р>1>π(х)Р>1> = Р>1>π(х).
Следовательно, Р>1>π(х) = π(х)Р>1>; операторы Р>1> и π(х) коммутируют.
Обратно, если эти операторы
перестановочны, то для f Н>1>
Н>1>
Р>1>π(х)f = π(х)Р>1>f = π(х)f ;
Следовательно, также π(х)f
 Н>1>.
Это означает, что Н>1> –
инвариантное подпространство.
Н>1>.
Это означает, что Н>1> –
инвариантное подпространство.
Теорема 2.3. Замкнутая
линейная оболочка К
инвариантных подпрост-
ранств есть
также инвариантное подпространство.
Доказательство. Всякий элемент g из К есть предел конечных сумм вида
h = f>1> + … + f>n>, где f>1>, …, f>n> – векторы исходных подпространств. С другой стороны, π(х)h = π(х)f>1> +…+ π(х)f>n> есть сумма того же вида и имеет своим пределом π(х)g.
2.2. Прямая сумма представлений.
Пусть I
– произвольное множество. Пусть (π>i>)>i>> >>I>
- семейство представлений
*-алгебры А в
гильбертовом пространстве Н>i>
(i
>>I>
- семейство представлений
*-алгебры А в
гильбертовом пространстве Н>i>
(i I).
Пусть
I).
Пусть
|| π>i> (х) || ≤ с>х>
где с>х> – положительная константа, не зависящая от i.
Обозначим через Н прямую
сумму пространств Н>i>,
то есть Н =
 Н>i>.
В силу (2.1.) можно образовать
непрерывный линейный оператор π(х)
в Н, который индуцирует π>i>>
>(х) в каждом Н>i>.
Тогда отображение х → π(х)
есть представление А в Н,
называемое прямой суммой представлений
π>i>>
> и обозначаемое
Н>i>.
В силу (2.1.) можно образовать
непрерывный линейный оператор π(х)
в Н, который индуцирует π>i>>
>(х) в каждом Н>i>.
Тогда отображение х → π(х)
есть представление А в Н,
называемое прямой суммой представлений
π>i>>
> и обозначаемое
 π>i>>
>или π>1>
π>i>>
>или π>1> …..
….. π>n>
в случае конечного семейства представлений
(π>1>…..π>n>).
Если (π>i>)>i>>
π>n>
в случае конечного семейства представлений
(π>1>…..π>n>).
Если (π>i>)>i>> >>I>
– семейство представлений *-алгебры
А, совпадающих с представлением π,
и если CardI
= c, то представления
>>I>
– семейство представлений *-алгебры
А, совпадающих с представлением π,
и если CardI
= c, то представления
 π>i>
обозначается через сπ.
Всякое представление, эквивалентное
представлению этого типа, называется
кратным π.
π>i>
обозначается через сπ.
Всякое представление, эквивалентное
представлению этого типа, называется
кратным π.
Для доказательства следующего понадобится лемма Цорна. Напомним ее.
Лемма Цорна. Если в частично упорядоченном подмножестве Х всякое линейно упорядоченное подмножество имеет в Х верхнюю грань, то Х содержит максимальный элемент.
Теорема 2.4. Всякое представление есть прямая сумма цикличных представлений.
Доказательство. Пусть f>0> ≠ 0 – какой-либо вектор из Н. Рассмотрим совокупность всех векторов π(х)f>0>, где х пробегает всю *-алгебру А. Замыкание этой совокупности обозначим через Н>1>. Тогда Н>1> – инвариантное подпространство, в котором f>0> есть циклический вектор. Другими словами, Н>1> есть циклическое подпространство представления π.
Если Н>1> = H, то предложение доказано; в противном случае H-Н>1> есть отличное от {0} инвариантное подпространство. Применяя к нему тот же прием, мы выделим циклическое подпространство Н>2> ортогональное Н>1>.
Обозначим через М
совокупность всех систем {Н>α>},
состоящих из взаимно ортогональных
циклических подпространств представления;
одной из таких систем является построенная
выше система {Н>1>,
Н>2>}.
Упорядоченная при помощи соотношения
включения совокупность М
образует частично упорядоченное
множество, удовлетворяющее условиям
леммы Цорна; именно, верхней гранью
линейно упорядоченного множества систем
{Н>α>} М
будет объединение этих систем. Поэтому
в М существует
максимальная система {Н>α>}.
Но тогда Н=
М
будет объединение этих систем. Поэтому
в М существует
максимальная система {Н>α>}.
Но тогда Н=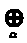 Н>α>;
в противном случае в инвариантном
подпространстве Н-(
Н>α>;
в противном случае в инвариантном
подпространстве Н-(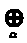 Н>α>)
существовало бы отличное от {0} циклическое
подпространство Н>0>
и мы получили бы систему {Н>α>}
Н>α>)
существовало бы отличное от {0} циклическое
подпространство Н>0>
и мы получили бы систему {Н>α>} Н>0>
Н>0> М,
содержащую максимальную систему {Н>α>},
что невозможно.
М,
содержащую максимальную систему {Н>α>},
что невозможно.
2.3. Неприводимые представления.
Определение 2.5. Представление называется неприводимым, если в пространстве Н не существует инвариантного подпространства, отличного от {0} и всего Н.
Согласно теореме 2.2. это означает, что всякий оператор проектирования, перестановочный со всеми операторами представления, равен 0 или 1.
Всякое представление в одномерном пространстве неприводимо.
Теорема 2.5. Представление π в пространстве Н неприводимо тогда и только тогда, когда всякий отличный от нуля вектор пространства Н есть циклический вектор этого представления.
Доказательство. Пусть представление
π неприводимо.
При f Н,
f
≠ 0, подпространство,
натянутое на векторы π(х)f
, х
Н,
f
≠ 0, подпространство,
натянутое на векторы π(х)f
, х А,
есть инвариантное подпространство; в
силу неприводимости представления оно
совпадает с {0} или Н.
Но первый случай невозможен, ибо тогда
одномерное пространство
А,
есть инвариантное подпространство; в
силу неприводимости представления оно
совпадает с {0} или Н.
Но первый случай невозможен, ибо тогда
одномерное пространство
{α
f
| α
 C}
инвариантно и потому совпадает с Н,
то есть π(х)=0 в
Н. Во втором
же случае f
есть циклический вектор.
C}
инвариантно и потому совпадает с Н,
то есть π(х)=0 в
Н. Во втором
же случае f
есть циклический вектор.
Обратно, если представление π приводимо и К – отличное от {0} и Н инвариантное подпространство в Н, то никакой вектор f из К не будет циклическим для представления π в Н.
Теорема 2.6. (И.Шур) Представление π неприводимо тогда и только тогда, когда коммутант π (А) в L(H) сводится к скалярам (то есть операторам кратным единичному).
Доказательство. Пусть представление
π неприводимо и пусть
ограни-
ченный оператор В перестановочен
со всеми операторами π(х).
Предположим сначала, что В – эрмитов
оператор; обозначим через E(λ)
спектральные проекторы оператора В.
Тогда при любом λ оператор E(λ)
перестановочен со всеми операторами
π(х) ; в виду неприводимости
представления E(λ) =0 или
E(λ) =1, так как (E(λ)
f, f)
не убывает при возрастании λ, то отсюда
следует, что существует λ>0> такое,
что E(λ) =0 при λ<λ>0>
и E(λ) =1 при λ>λ>0> .
Отсюда
В= λ
dE(λ)
= λ>0> 1.
λ
dE(λ)
= λ>0> 1.
Пусть теперь В – произвольный
ограниченный оператор, переста-
новочный
со всеми операторами π(х).
Тогда В* также перестановочен со всеми
операторами π(х).
Действительно,
В*π(х) = (π(х*)В)* = (Вπ(х*))* = π(х)В*
Поэтому эрмитовы операторы В>1>= ,
В>2>=
,
В>2>= также перестановочны со всеми операторами
π(х)
и, следовательно, кратны единице. Но
тогда и оператор В = В>1>+iВ>2>
кратен единице, то есть В – скаляр.
также перестановочны со всеми операторами
π(х)
и, следовательно, кратны единице. Но
тогда и оператор В = В>1>+iВ>2>
кратен единице, то есть В – скаляр.
Обратно, пусть всякий ограниченный оператор, перестановочный со всеми операторами π(х), кратен единице. Тогда, в частности, всякий оператор проектирования, перестановочный со всеми операторами π(х) кратен единице. Но оператор проектирования может быть кратным единице только тогда, когда он равен 0 или 1. Следовательно, представление неприводимо.
Определение 2.6
Всякий линейный оператор Т
: Н →
Н΄ такой, что Тπ(х)=π΄(х)Т
для любого х А,
называется оператором сплетающим π
и π΄.
А,
называется оператором сплетающим π
и π΄.
Пусть Т : Н → Н΄ - оператор, сплетающий π и π΄. Тогда Т* : Н΄ → Н является оператором, сплетающим π΄ и π, так как
Т* π΄(х) = (π΄(х)Т)* = (Тπ(х*))* = π(х)Т*
Отсюда получаем, что
Т* Тπ(х)=Т* π΄(х)Т= π(х)Т*Т (2.1.)
Поэтому |T|
= (T*T)1/2
перестановочен с π(А).
Пусть Т = U|T|
- полярное разложение Т.
Тогда для любого х А
А
Uπ(х)|T| = U|T| π(х)= Тπ(х)= π΄(х)Т=π΄(х)U|T| (2.2.)
Если KerT={0}, то |T| (Н) всюду плотно в Н и из (2.2.) следует
Uπ(х) = π΄(х)U (2.3.)
Если, кроме того,
 =
Н΄, то есть
если KerT*={0},
то U
является изоморфизмом Н
и Н΄ и (2.3.)
доказывает что π и
π΄
эквивалентны.
=
Н΄, то есть
если KerT*={0},
то U
является изоморфизмом Н
и Н΄ и (2.3.)
доказывает что π и
π΄
эквивалентны.
Пусть π и π΄ - неприводимые представления *-алгебры А в гильбертовых пространствах Н и Н΄ соответственно. Допустим, что существует ненулевой сплетающий оператор Т : Н → Н΄. Тогда из (2.1.) и теоремы 2.6. следует, что Т*Т и ТТ* - скалярны (≠0) и π, π΄ эквивалентны.
2.4. Конечномерные представления.
Теорема 2.7. Пусть
π – конечномерное
представление *-алгебры А.
Тогда π = π>1> …..
….. π>n>
, где π>i>>
>неприводимы.
π>n>
, где π>i>>
>неприводимы.
Доказательство. Если dimπ
= 0 (n=0),
то все доказано. Предположим, что dimπ
= q
и что наше предложение доказано при
dimπ<q.
Если π неприводимо,
то предложение снова доказано. В противном
случае π = π΄
 π΄΄,
причем dimπ΄<q,
dimπ΄΄<q,
и достаточно применить предположение
индукции.
π΄΄,
причем dimπ΄<q,
dimπ΄΄<q,
и достаточно применить предположение
индукции.
Разложение π =
π>1> …..
….. π>n>
не единственно. Тем не менее,
мы получим некоторую теорему единственности.
π>n>
не единственно. Тем не менее,
мы получим некоторую теорему единственности.
Пусть ρ>1>,
ρ>2>
– два неприводимых подпредставления
π. Им отвечают
инвариантные подпространства Н>1>
и Н>2>.
Пусть Р>1> и
Р>2> – проекторы
Н на Н>1>
и Н>2>.
Они коммутируют с π(А).
Поэтому ограничение Р>2>
на Н>1>
есть оператор, сплетающий ρ>1>
и ρ>2>.
Следовательно, если Н>1>
и Н>2>
не ортогональны, то из
пункта 2.3. следует, что ρ>1>
и ρ>2>
эквивалентны. Это доказывает, что любое
неприводимое подпредставление π
эквивалентно одному из π>i>>
>. Итак, перегруп-
пировав
π>i>>
>, получаем, что π
= ν>1> …..
….. ν>m>,
где каждое ν>i>
есть кратное ρ>i>ν>i>΄
неприводимого представления ν>i>΄,
и ν>i>΄
попарно эквивалентны. Если ρ
– неприводимое представление π,
то предыдущее рассуждение показывает,
что соответствующее инвариантное
подпространство Н΄
ортогонально всем инвариантным
подпространствам Н>i>,
отвечающих ν>i>,
кроме одного. Поэтому Н΄
содержится в одном из Н>i>.
Это доказывает, что каждое пространство
Н>i>
определяется однозначно: Н>i>
– это подпространство Н,
порожденное пространствами подпредставлений
π, эквивалентных
ν>i>΄.
Таким образом, доказано предложение.
ν>m>,
где каждое ν>i>
есть кратное ρ>i>ν>i>΄
неприводимого представления ν>i>΄,
и ν>i>΄
попарно эквивалентны. Если ρ
– неприводимое представление π,
то предыдущее рассуждение показывает,
что соответствующее инвариантное
подпространство Н΄
ортогонально всем инвариантным
подпространствам Н>i>,
отвечающих ν>i>,
кроме одного. Поэтому Н΄
содержится в одном из Н>i>.
Это доказывает, что каждое пространство
Н>i>
определяется однозначно: Н>i>
– это подпространство Н,
порожденное пространствами подпредставлений
π, эквивалентных
ν>i>΄.
Таким образом, доказано предложение.
Теорема 2.8. В
разложении π =
ρ>1>ν>1>΄ …..
….. ρ>m>ν>m>΄
представления π,
(где ν>1>΄,…,
ν>m>΄
неприводимы и неэквивалентны) целые
числа ρ>i>
и классы представлений ν>i>΄
определяются единственным образом,
как и пространства представлений.
ρ>m>ν>m>΄
представления π,
(где ν>1>΄,…,
ν>m>΄
неприводимы и неэквивалентны) целые
числа ρ>i>
и классы представлений ν>i>΄
определяются единственным образом,
как и пространства представлений.
2.5. Интегрирование и дезинтегрирование представлений. Напомним определение борелевского пространства.
Определение 2.7.
Борелевским пространством называется
множество Т,
снабженное множеством В
подмножеств Т,
обладающим следующими свойствами: Т В,
Ø
В,
Ø В,
В инвариантно относительно счетного
объединения, счетного пересечения и
перехода к дополнению.
В,
В инвариантно относительно счетного
объединения, счетного пересечения и
перехода к дополнению.
Определение 2.8. Пусть Т>1>, Т>2> – борелевские пространства. Отображение f: Т>1>→Т>2> называется борелевским, если полный прообраз относительно f любого множества в Т>2> есть борелевское множество в Т>1>.
Дадим несколько вспомогательных определений и утверждений.
Пусть Т – борелевское пространство и μ – положительная мера на Т.
Определение 2.9. μ
– измеримое поле гильбертовых пространств
на Т есть пара
ε =
((H(t))>t>> >>T>,
Г), где (H(t))>t>>
>>T>,
Г), где (H(t))>t>> >>T>
– семейство гильбертовых пространств,
индексы которых пробегают Т,
а Г – множество
векторных полей, удовлетворяющее
следующим условиям:
>>T>
– семейство гильбертовых пространств,
индексы которых пробегают Т,
а Г – множество
векторных полей, удовлетворяющее
следующим условиям:
(i)
Г – векторное
подпространство
 Н(t);
Н(t);
существует последовательность
(х>1>,
х>2>,…)
элементов Г
таких, что для любого t T
элементы х>n>(t)
образуют последовательность H(t);
T
элементы х>n>(t)
образуют последовательность H(t);
для любого х Г
функция t→||x(t)||
μ – измерима;
Г
функция t→||x(t)||
μ – измерима;
пусть х
– векторное поле; если для любого y Г
функция t→(x(t),
y(t))
μ – измерима,
то х
Г
функция t→(x(t),
y(t))
μ – измерима,
то х Г.
Г.
Пусть ε =
((H(t))>t>> >>T>,
Г) μ – измеримое поле гильбертовых
пространств на Т. Векторное поле х
называется полем с интегрируемым
квадратом, если х
>>T>,
Г) μ – измеримое поле гильбертовых
пространств на Т. Векторное поле х
называется полем с интегрируемым
квадратом, если х Г
и
Г
и
 ||x(t)||2
dμ(t)
< +∞.
||x(t)||2
dμ(t)
< +∞.
Если х,
y
– с интегрируемым квадратом, то х+y
и λх (λ С)
– тоже и функция t
→(x(t),
y(t))
интегрируема; положим
С)
– тоже и функция t
→(x(t),
y(t))
интегрируема; положим
(x, y)
=
 (x(t),
y(t)) dμ(t)
(x(t),
y(t)) dμ(t)
Тогда векторные поля с интегрируемым
квадратом образуют гильбертово
пространство Н,
называемое прямым интегралом Н(t)
и обозначаемое
 x(t)dμ(t).
x(t)dμ(t).
Определение 2.10.
Пусть ε =
((H(t))>t>> >>T>,
Г)
– измеримое поле гильбер-
>>T>,
Г)
– измеримое поле гильбер-
товых
пространств на Т.
Пусть для любого t T
определен оператор S(t)
T
определен оператор S(t) L(H(t)).
Если для любого х
L(H(t)).
Если для любого х T
поле t→S(t)x(t)
измеримо, то t→S(t)
называется измеримым операторным полем.
T
поле t→S(t)x(t)
измеримо, то t→S(t)
называется измеримым операторным полем.
Пусть Т
– борелевское пространство, μ
- положительная мера на
Т, t→Н(t)
- μ - измеримое
поле гильбертовых пространств на Т.
Пусть для каждого t T
задано представление π(t)
*-алгебры А в
Н(t):
говорят, что t→π(t)
есть поле представлений А.
T
задано представление π(t)
*-алгебры А в
Н(t):
говорят, что t→π(t)
есть поле представлений А.
Определение 2.11.
Поле представлений t→π(t)
называется измеримым, если для каждого
х А
поле операторов t→π(t)х
измеримо.
А
поле операторов t→π(t)х
измеримо.
Если поле представлений t→π(t)
измеримо, то для каждого х А
можно образовать непрерывный оператор
π(х)=
А
можно образовать непрерывный оператор
π(х)= π(t)
(x)
dμ(t)
в гильбертовом прост-
π(t)
(x)
dμ(t)
в гильбертовом прост-
ранстве Н
= Н(t)
dμ(t).
Н(t)
dμ(t).
Теорема 2.9. Отображение х→π(х) есть представление А в Н.
Доказательство. Для любых х,
y А
имеем
А
имеем
π(х+y)
=
 π(t)
(x+y) dμ(t)
=
π(t)
(x+y) dμ(t)
=
 (π(t)
(x) + π(t) (y))
dμ(t)
=
(π(t)
(x) + π(t) (y))
dμ(t)
= π(t)
(x )dμ(t)
+
π(t)
(x )dμ(t)
+
+ π(t)
(y)
dμ(t)
= π(х) +π(y)
π(t)
(y)
dμ(t)
= π(х) +π(y)
Аналогично π(λх) = λπ(х), π(хy) = π(х) π(y), π(х*)=π(х)*
Определение 2.12.
В предыдущих обозначениях
π называется
прямым интегралом π(t)
и обозначается π
= π(t)
dμ(t).
π(t)
dμ(t).
Определение 2.13.
Операторное поле t→φ(t)I(t) L(H(t))
где I(t)-единичный
оператор в H(t),
называется диагональным оператором в
Н=
L(H(t))
где I(t)-единичный
оператор в H(t),
называется диагональным оператором в
Н= Н(t)dμ(t).
Н(t)dμ(t).
Пусть ε =
((H(t))>t>> >>T>,
Г) – μ-измеримое поле гильбертовых
пространств на Т, μ>1> – мера
на Т, эквивалентная μ (то есть
каждая из мер μ>1>, μ абсолютно
непрерывна по другой), и ρ(t)=
>>T>,
Г) – μ-измеримое поле гильбертовых
пространств на Т, μ>1> – мера
на Т, эквивалентная μ (то есть
каждая из мер μ>1>, μ абсолютно
непрерывна по другой), и ρ(t)= .
Тогда отображение, которое каждому
х
.
Тогда отображение, которое каждому
х Н==
Н== Н(t)dμ(t)
составляет поле t→ρ(t)-1/2х(t)Н>1>=
Н(t)dμ(t)
составляет поле t→ρ(t)-1/2х(t)Н>1>= Н(t)
dμ>1>(t),
Н(t)
dμ>1>(t),
есть изометрический изоморфизм Н на Н>1>, называемый каноническим.
Действительно,
|| ρ(t)-1/2х(t)dμ>1>(t)||2
=
ρ(t)-1/2х(t)dμ>1>(t)||2
=
 ||х(t)||2ρ(t)-1
dμ>1>(t)
=
||х(t)||2ρ(t)-1
dμ>1>(t)
=
 ||х(t)||2dμ>1>(t)
= ||х(t)||2
||х(t)||2dμ>1>(t)
= ||х(t)||2
Теорема 2.10. Пусть Т – борелевское пространство, μ – мера на Т, t→Н(t) – измеримое поле гильбертовых пространств на Т, t→π(t) – измеримое поле представлений А в Н(t),
Н = Н(t)
dμ(t)
, π>1>==
Н(t)
dμ(t)
, π>1>== π(t
)dμ(t),
π(t
)dμ(t),
Д – алгебра диагональных операторов в Н. Пусть μ>1> – мера на Т, эквивалентная μ,
Н>1>
= Н(t)
dμ>1>(t)
, π>1 >=
Н(t)
dμ>1>(t)
, π>1 >= π(t)
dμ>1>(t),
π(t)
dμ>1>(t),
Д>1> – алгебра диагональных операторов в Н>1>. Тогда канонический изоморфизм преобразует π в π>1> и Д в Д>1>.
Доказательство. Пусть ρ(t)= .
Канонический изоморфизм из Н
в Н>1>
есть изометрический
изоморфизм, который переводит х
=
.
Канонический изоморфизм из Н
в Н>1>
есть изометрический
изоморфизм, который переводит х
= x(t)
dμ(t)
x(t)
dμ(t) Н
в
Н
в
Ux>
>=
 ρ-1/2х(t)
dμ>1>(t).
ρ-1/2х(t)
dμ>1>(t).
Пусть α
 А.
Имеем
А.
Имеем
π>1>(α)Ux
=
 π(t)(α)
ρ-1/2 х(t)
dμ>1>(t)
= U
π(t)(α)
ρ-1/2 х(t)
dμ>1>(t)
= U π(t)(α)
х(t)
dμ(t)
= Uπ(α)x,
π(t)(α)
х(t)
dμ(t)
= Uπ(α)x,
поэтому и преобразуем π
в π>1>.
Тогда если S Д,
то аналогично SUx
= USx,
для любого х
Д,
то аналогично SUx
= USx,
для любого х Н.
Н.
Определение 2.14.
Пусть Т, Т>1>
– борелевские пространства; μ,
μ>1>
– меры на Т и
Т>1>
соответственно; ε
= ((H(t))>t>> >>T>,
Г), Z>1>
= ((H>1>(t>1>))>t>>1>>
>>T>,
Г), Z>1>
= ((H>1>(t>1>))>t>>1>> >>T>>1>,
Г), - μ-измеримое
и μ>1>-измеримое
поля гильбертовых пространств. Пусть
η: Т→Т>1>
– борелевский изоморфизм, переводящий
μ в μ>1>;
η-изоморфизм
ε на ε>1>
называется семейство (V(t))>t>>
>>T>>1>,
Г), - μ-измеримое
и μ>1>-измеримое
поля гильбертовых пространств. Пусть
η: Т→Т>1>
– борелевский изоморфизм, переводящий
μ в μ>1>;
η-изоморфизм
ε на ε>1>
называется семейство (V(t))>t>> >>T>,
обладающее следующими
свойствами:
>>T>,
обладающее следующими
свойствами:
для любого t T
отображение V(t)
является изоморфизмом Н(t)
на Н>1>(η(t));
T
отображение V(t)
является изоморфизмом Н(t)
на Н>1>(η(t));
для того, чтобы поле векторов
t→x(t) H(t)
на Т было
μ-измеримо,
необходимо и достаточно, чтобы поле
η(t)→V(t)х(t)
H(t)
на Т было
μ-измеримо,
необходимо и достаточно, чтобы поле
η(t)→V(t)х(t)
 Н>1>(η(t))
на Т>1>
было μ>1>-измеримо.
Н>1>(η(t))
на Т>1>
было μ>1>-измеримо.
Отображение, переводящее
поле х Н
=
Н
= Н(t)
dμ(t) в поле
η(t))→V(t)х(t)
Н(t)
dμ(t) в поле
η(t))→V(t)х(t)
 Н>1>
=
Н>1>
=
 Н>1>(t)
dμ>1>(t)
, есть изоморфизм Н на Н>1>,
обозначаемый
Н>1>(t)
dμ>1>(t)
, есть изоморфизм Н на Н>1>,
обозначаемый
 V(t)
dμ(t).
V(t)
dμ(t).
Теорема 2.11. Пусть Т – борелевское пространство; μ – мера на Т, t→H(t) – μ- измеримое поле гильбертовых пространств на Т, t→ π(t) - μ- измеримое поле представлений А в H(t),
Н = Н(t)
dμ(t),
π ==
Н(t)
dμ(t),
π == π(t)
dμ(t),
π(t)
dμ(t),
Д – алгебра диагональных операторов в Н. Определим аналогичным образом Т>1>, μ>1>, t>1>→H>1>(t>1>), t>1>→ π>1>(t>1>), Н>1>, π>1>, Д>1>.
Предположим, что существует:
N, N>1> – борелевские подмножества Т и Т>1>, такие что μ (N) = μ (N>1>) = 0;
борелевский изоморфизм η: T\N →T\N>1>, преобразует μ в μ>1>;
η-изоморфизм
t→V(t)
поля t→Н(t)
(t Z\N)
на поле t>1>→Н>1>(t>1>)
(t>1>
Z\N)
на поле t>1>→Н>1>(t>1>)
(t>1> Т>1>\N>1>)
такой, что V(t)
преобразует π(t)
в π>1>(η(t))
для каждого t.
Т>1>\N>1>)
такой, что V(t)
преобразует π(t)
в π>1>(η(t))
для каждого t.
Тогда V
= V(t)dμ(t)
преобразует Д в Д>1> и π
в π>1>.
V(t)dμ(t)
преобразует Д в Д>1> и π
в π>1>.
Доказательство. Обозначим через
I>t>,
I>t>>1>
единичные операторы в Н(t)
и Н>1>(t>1>).
Если f L∞(T,
μ) и если f>1>
– функция на Т>1>\N>1>,
получаемая из f|(T\N)
при помощи η,
то V
преобразует
L∞(T,
μ) и если f>1>
– функция на Т>1>\N>1>,
получаемая из f|(T\N)
при помощи η,
то V
преобразует
 f(t)I>t>>
>dμ(t)
в
f(t)I>t>>
>dμ(t)
в
 f>1>(t>1>)
I>t>>1
>dμ>1>(t>1>),
поэтому V
преоб-
f>1>(t>1>)
I>t>>1
>dμ>1>(t>1>),
поэтому V
преоб-
разует Д
в Д>1>.
С другой стороны, пусть α А
и х =
А
и х =
 х(t)
dμ(t)
х(t)
dμ(t) Н.
Н.
Тогда
Vπ(α)х
= V π(t)(α)
х(t)
dμ(t)
=
π(t)(α)
х(t)
dμ(t)
=
 V(η-1(t>1>))
π(η-1(t>1>))(α)
х(η-1(t>1>))
dμ>1>(t>1>)
=
V(η-1(t>1>))
π(η-1(t>1>))(α)
х(η-1(t>1>))
dμ>1>(t>1>)
=
 π>1>(t>1>)(α)
V(η-1(t>1>))
х(η-1(t>1>))
dμ>1>(t>1>)
= π>1 >(α)
V
х
π>1>(t>1>)(α)
V(η-1(t>1>))
х(η-1(t>1>))
dμ>1>(t>1>)
= π>1 >(α)
V
х
Поэтому V преобразует π в π>1>.
Приведем примеры прямых интегралов.
Пусть имеется последовательность
гильбертовых пространств
 и дискретная мера μ
на N,
то есть μ(n)=1
для любого n
и дискретная мера μ
на N,
то есть μ(n)=1
для любого n N.
Тогда
N.
Тогда
 Н(n)
dμ(n)
=
Н(n)
dμ(n)
=
 Н(n),
то есть прямой интеграл сводится к
ортогональ-
Н(n),
то есть прямой интеграл сводится к
ортогональ-
ной сумме.
Пусть Т=[0,
1] и в каждой точке t Т
соответствует поле комплексных чисел
С, и на Т
задана линейная мера Лебега dt.
Тогда
Т
соответствует поле комплексных чисел
С, и на Т
задана линейная мера Лебега dt.
Тогда
 С
dt
= L>2>
(0, 1).
С
dt
= L>2>
(0, 1).
Изоморфизм устанавливается
отображением х =
 х(t)
dt →х(t)
х(t)
dt →х(t) L>2>
(0, 1).
L>2>
(0, 1).
Разложения представления на неприводимые представления в прямой интеграл называют дезинтегрированием.
§ 3. Тензорные произведения пространств
3.1. Тензорные произведения
пространств. Пусть
 - конечная последовательность сепарабельных
гильбертовых пространств,
- конечная последовательность сепарабельных
гильбертовых пространств,
 - некоторый ортонормированный базис в
Н>к>.
- некоторый ортонормированный базис в
Н>к>.
Образуем формальное произведение
 (3.1.)
(3.1.)
α = (α>1>,…,
α>n>)

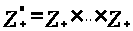 (n раз), то есть рассмотрим
упорядо-
(n раз), то есть рассмотрим
упорядо-
ченную последовательность
(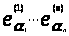 ) и на формальные векторы (3.1.) натянем
гильбертово пространство, считая, что
они образуют его ортонормиро-
) и на формальные векторы (3.1.) натянем
гильбертово пространство, считая, что
они образуют его ортонормиро-
ванный
базис. Полученное сепарабельное
гильбертово пространство называется
тензорным произведением пространств
Н>1>,…, Н>n>
и обозначается Н>1> ,…,
,…,
 Н>n>
=
Н>n>
=

 .
Его векторы имеют вид:
.
Его векторы имеют вид:
f =
 (f>α>
(f>α> C),
|| f ||2
=
C),
|| f ||2
= <
∞ (3.2.)
<
∞ (3.2.)
Пусть g
=



 ,
тогда скалярное произведение опреде-
,
тогда скалярное произведение опреде-
ляется
формулой
(f,
g) =
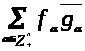 (3.3.)
(3.3.)
Пусть f(k)
=


 (к
= 1,…, n) – некоторые векторы.
По определению
(к
= 1,…, n) – некоторые векторы.
По определению
f
= f(1) >…>
>…> >
>f(n)
=
>
>f(n)
=
 (3.4.)
(3.4.)
Коэффициенты f>α>>
>=
 разложения (3.4.) удовлетворяют условию
(3.2.), поэтому вектор (3.4.) принадлежит
разложения (3.4.) удовлетворяют условию
(3.2.), поэтому вектор (3.4.) принадлежит

 ,
при этом
,
при этом
|| f || =
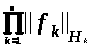 (3.5.)
(3.5.)
Функция Н>1> ,…,
,…,
 Н>n>
Н>n>
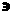 <
< >
>
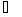



 линейна по каждому фрагменту, а линейная
оболочка L векторов
(3.4.) плотна в
линейна по каждому фрагменту, а линейная
оболочка L векторов
(3.4.) плотна в

 - эта линейная оболочка называется
алгебраическим (непополненным) тензорным
произведением пространств Н>1>,…,
Н>n> и
обозначается α.
- эта линейная оболочка называется
алгебраическим (непополненным) тензорным
произведением пространств Н>1>,…,
Н>n> и
обозначается α.


Приведенное определение тензорного
произведения зависит от выбора
ортогонального базиса
 в
каждом сомножителе
в
каждом сомножителе
 .
При изменении базисов получаем тензорное
произведение, изоморфное с сохранением
своей структуры исходному произведению.
.
При изменении базисов получаем тензорное
произведение, изоморфное с сохранением
своей структуры исходному произведению.
Пусть Н>1> и Н>2>
– гильбертовы сепарабельные пространства.
Тогда конструкция тензорного произведения
означает следующее. Рассматривается
линейная оболочка L
формальных произведений f>1> f>2>,
причем считается, что
f>2>,
причем считается, что
(f>1>
+ g>1>) f>2>
= f>1>
f>2>
= f>1> f>2>
+ g>1>
f>2>
+ g>1> f>2>
(3.6.)
f>2>
(3.6.)
f>1> (f>2>
+ g>2>)
= f>1>
(f>2>
+ g>2>)
= f>1> f>2>
+ f>1>
f>2>
+ f>1> g>2>
(3.7.)
g>2>
(3.7.)
(λ f>1>) f>2>=λ
(f>1>
f>2>=λ
(f>1> f>2>)
(3.8.)
f>2>)
(3.8.)
f>1> λ (f>2>)
= λ (f>1>
λ (f>2>)
= λ (f>1> f>2>)
(3.9.)
f>2>)
(3.9.)
f>1>,
g>1> Н>1>;
f>2>,
g>2 >
Н>1>;
f>2>,
g>2 >
 Н>2>;
λ
Н>2>;
λ
 С.
С.
Иными словами, линейное пространство L факторизируется по его линейному подмножеству, натянутому на всевозможные векторы, имеющие вид разностей между правыми и левыми частями равенств (3.6.) – (3.9.).
Затем вводится скалярное произведение в L.
(f>1> f>2>
, g>1>
f>2>
, g>1> g>2>
) = (f>1>
g>1>)(f>2>
g>2>)
(3.10.)
g>2>
) = (f>1>
g>1>)(f>2>
g>2>)
(3.10.)
f>1>,
g>1> Н>1>;
f>2>,
g>2 >
Н>1>;
f>2>,
g>2 >
 Н>2>,
Н>2>,
а затем распространяется на другие элементы из факторизованного L билинейным образом.
3.2. Тензорные произведения операторов. Определим тензорное произведение ограниченных операторов.
Теорема 3.1. Пусть
 ,
,
 - две последовательности гильбер-
- две последовательности гильбер-
товых
пространств,
 - последовательность операторов А>к>
- последовательность операторов А>к> L(Н>к>,
G>к>). Определим
тензорное произведение А>1>
L(Н>к>,
G>к>). Определим
тензорное произведение А>1> …
… А>n>
=
А>n>
=
 А>к>
формулой
А>к>
формулой
(
 )
f =
)
f =

 (
( )
=
)
=
 (3.11.)
(3.11.)
(f


 ).
).
Утверждается, что ряд в правой
части (3.11.) сходится слабо в

 и
определяет оператор
и
определяет оператор


 L (
L (
 ,
,

 ),
причем
),
причем
||

 ||
=
||
=
 ||
||
 ||
(3.12.)
||
(3.12.)
Доказательство. Достаточно
рассмотреть случай n=2,
так как в силу равенства Н>1> ,…,
,…,
 Н>n>
= (Н>1>
Н>n>
= (Н>1> ,…,
,…,
 Н>n>>-1>)
Н>n>>-1>) Н>n>
общий случай получается по индукции.
Н>n>
общий случай получается по индукции.
Пусть
 -
некоторый ортонормированный базис в
G>к> (к =
1, 2) и пусть g =
-
некоторый ортонормированный базис в
G>к> (к =
1, 2) и пусть g =
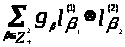
 G>1>
G>1> G>2>. В
качестве f
возьмем вектор из Н>1>
G>2>. В
качестве f
возьмем вектор из Н>1> Н>2> с конечным числом отличных
от нуля координат f>α>.
Н>2> с конечным числом отличных
от нуля координат f>α>.
Зафиксируем α>2>,
β>1 >
 Z>+> и обозначим через
f(α>2>)
Z>+> и обозначим через
f(α>2>)
 Н>1>
вектор f(α>2>)
=
Н>1>
вектор f(α>2>)
=
 и через g(β>1>)
и через g(β>1>) G>2>
– вектор g(β>1>)
=
G>2>
– вектор g(β>1>)
= .
Получим
.
Получим
 =
=
 =
=
=
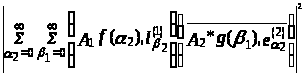 ≤
≤
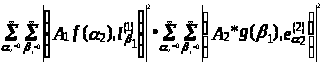 =
=
=
 ≤
≤
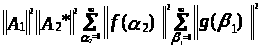 =
=
=

Из этого неравенства следует
слабая сходимость в G>1> G>2>
ряда
G>2>
ряда
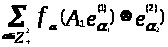 уже при произвольном c
уже при произвольном c
 Н>1>
Н>1> Н>2>
и оценка его нормы в G>1>
Н>2>
и оценка его нормы в G>1> G>2>
сверху через ||A>1>||
||A>2>|| ||f||.
Таким образом, оператор A>1>
G>2>
сверху через ||A>1>||
||A>2>|| ||f||.
Таким образом, оператор A>1> A>2>: Н>1>
A>2>: Н>1> Н>2> →G>1>
Н>2> →G>1> G>2>
определен посредством (3.11.) корректно,
ограничен и его норма не превосходит
||A>1>|| ||A>2>||.
G>2>
определен посредством (3.11.) корректно,
ограничен и его норма не превосходит
||A>1>|| ||A>2>||.
Из (3.5.) и (3.11.) следует
||(A>1> A>2>) (f>1>
A>2>) (f>1> f>2>)||
= ||A>1> >
>f>1>||
||A>2>
f>2>||
(f>к>
f>2>)||
= ||A>1> >
>f>1>||
||A>2>
f>2>||
(f>к>
 Н>к>
, к = 1, 2)
Н>к>
, к = 1, 2)
Подбирая должным образом орты
f>1>,
f>2>
последнее произведение можно сделать
сколь угодно близким к ||A>1>||
||A>2>||, поэтому
неравенство ||(A>1> A>2>)|| ≤
||A>1>|| ||A>2>||
не может выполняться, то есть (3.12.) при
n=2 доказано.
A>2>)|| ≤
||A>1>|| ||A>2>||
не может выполняться, то есть (3.12.) при
n=2 доказано.
Из (3.11.) получаем для А>к>
 L(H>к>,
G>к>), В>к>
L(H>к>,
G>к>), В>к>
 L(H>к>,
G>к>) (к = 1,…,
n) соотношения
L(H>к>,
G>к>) (к = 1,…,
n) соотношения
( В>к>)
(
В>к>)
( А>к>)
=
А>к>)
=
 (В>к>
А>к>)
(3.13.)
(В>к>
А>к>)
(3.13.)
( А>к>)*
=
А>к>)*
=
 А>к>*
(3.14)
А>к>*
(3.14)
( А>к>)
(f>1>
А>к>)
(f>1> …
… f>n>)
= A>1>
> >f>1>
f>n>)
= A>1>
> >f>1> …
… A>n>
> >f>n>
(3.15.)
A>n>
> >f>n>
(3.15.)
(f>к>
 H>к>;
к = 1,…, n)
H>к>;
к = 1,…, n)
(3.15) однозначно определяет
оператор
 А>к>.
А>к>.
Приведем пример. Пусть H>к>
= L2( (0,1),
d (
(0,1),
d ( m>к>))
= L2
m>к>))
= L2
Действительно, вектору вида
(3.1.)



 поставим в соответствие функцию
поставим в соответствие функцию

 L2.
Такие функции образуют ортонормированный
базис пространства L2,
поэтому такое соответствие порождает
требуемый изоморфизм между
L2.
Такие функции образуют ортонормированный
базис пространства L2,
поэтому такое соответствие порождает
требуемый изоморфизм между

 и
L2.
и
L2.
Глава II. Задача о двух ортопроекторах
§ 1. Два ортопроектора в унитарном пространстве
Постановка задачи. Пусть дана *-алгебра P>2>
P>2 > = С < р>1>, р>2>> >| р>1>2 = р>1>* = р>1>, р>2>2 =р>2>* = р>2> >
порожденная двумя проекторами, то есть двумя идемпотентными самосопряженными элементами.
Положим u = 2p>1> – 1, v = 2p>2> – 1, тогда u, v самосопряженные элементы.
u2 = (2p>1> – 1)2 = 4p>1> – 4p>1> + 1 = 1, v2 = 1. Таким образом u, v – унитарные самосопряженные элементы.
Тогда *-алгебру P>2 > можно задать иначе:
P>2> = С < p>1>*= p>1>, p>2>*=p>2> | p>1>2 = p>1>, p>2>2 = p>2> > = C <u* = u, v* = v | u2 = 1, v2 =1 >
Это групповая *-алгебра, порожденная двумя унитарными самосопряженными элементами.
Требуется найти все неприводимые представления *-алгебры P>2 >, с точностью до унитарной эквивалентности.
1.2. Одномерные *-представления *-алгебры P>2 >. Пусть π: P>2> →L(H) - *-представление *-алгебры P>2 >. Рассмотрим сначала случай, когда dim H = 1, то есть dim π = 1.
P>2> = С < р>1>, р>2>> >| р>1>2 = р>1>* = р>1>, р>2>2 =р>2>* = р>2> >
Обозначим через Р>к> = π(р>к>),
к = 1,2. Поскольку р>к>2=
р>к>* = р>к>
(к = 1, 2) и π - *-представление,
то Р>к>2 = Р>к>* = Р>к>
(к =1, 2) – ортопроекторы в Н на
подпространстве Н>к> = {y H
| Р>к> y = y
} к = 1, 2.
H
| Р>к> y = y
} к = 1, 2.
Возможны следующие случаи:
Н>1> = Н>2> = {0}; тогда Р>1> = 0, Р>2> = 0.
Н>1>> >= Н (то есть dim H>1> =1), Н>2> = {0}, тогда Р>1> = 1, Р>2> = 0.
Н>1> = {0}, Н>2> = Н (то есть dim H>2> =1), тогда Р>1> = 0, Р>2> = 1.
Н>1> = Н>2> = Н (dim H>1> = dim H>2>> >=1), тогда Р>1> = 1, Р>2 >= 1.
Так как dim H =1, то мы можем получить 4 одномерных неприводимых *-представлений P>2>, причем они неэквивалентны.
1.3. Двумерные *-представления
*-алгебры P>2
. > Обозначим через Н>к>
область значений оператора Р>к>
при к = 1,2. Пусть Н>к>┴
- ортогональное дополнение подпространства
Н>к> (к = 1,2) в Н. Тогда
Н=H>1> Н>1>┴
, Н=H>2>
Н>1>┴
, Н=H>2> Н>2>┴
Н>2>┴
Введем дополнительные обозначения :
Н>0,0>> >= Н>1>┴ ∩Н>2>┴, Н>0,1>> >= Н>1>┴ ∩Н>2>, Н>1,0>> >= Н>1> ∩Н>2>┴, Н>1,1>> >= Н>1> ∩Н>2>. (1.1.)
Пусть dim H = 2. предположим, что существуют i и j такие, что H>ij>> > нетривиально, то есть dim H>ij>> >> >=1. Пусть, например, dim Н>1,0>> >= 1 (остальные случаи аналогичны). Тогда в H существует ненулевой вектор h такой, что Н>1,0>> >= л.о. {h}, но тогда P>1>h = h, P>2>h = 0; следовательно Н>1,0>> >инвариантное подпространство. Значит в этом случае *-представление π не может быть неприводимым.
Будем считать, что H>ij>>
> ={0} для любых i
= 0, 1 и j =0, 1, (то есть
H>ij>>
> линейно независимы) и dim
H>1> = dim
H>2>> >=1.
Тогда в Н можно найти два ортогональных
базиса {e>1>,
e>2>} и {g>1>,
g>2>}, в
которых матрицы операторов Р>1> и
Р>2> имеют вид
 .
Найдем матрицу оператора Р>2> в
базисе {e>1>,
e>2>}.
.
Найдем матрицу оператора Р>2> в
базисе {e>1>,
e>2>}.
П усть
g>1>
= a>11>e>1>
+ a>12>
e>2>
усть
g>1>
= a>11>e>1>
+ a>12>
e>2>
 g>2>
= a>21>e>1>
+ a>22>e>2>
g>2>
= a>21>e>1>
+ a>22>e>2>
e>1> = b>11>g>1> + b>12>g>2>
e>2> = b>21>g>1> + b>22>g>2>
Рассмотрим векторы h>1> = eite>1> и h>2> = eile>2>, тогда
|| h>1 >|| = || eite>1 >|| = || e>1> || = 1, || h>2 >|| = || eile>2 >|| = || e>2> || = 1
(h>1 >,h>2> ) = (eite>1> , eile>2>) = ei(t-l)(e>1>, e>2> ) = 0, то есть {h>1 >,h>2>} – ортонормированный базис.
Р>1>h>1> =ei t Р>1 > e>1> = h>1>, Р>1>h>2> =eil Р>1 > e>2> = 0.
Значит в базисе {h>1
>,h>2>}
матрица оператора Р>1> также имеет
вид
 .
Тогда можно считать, что a>11>,
a>12> > 0
(так как, например, a>11
>e>1>=|a>11>|
eite>1>
=|a>11>| h>1>)
.
Тогда можно считать, что a>11>,
a>12> > 0
(так как, например, a>11
>e>1>=|a>11>|
eite>1>
=|a>11>| h>1>)
(e>1>,
e>2> )
= 0, значит a>11>
a>21> = a>12>
a>22> =
0 или
 ,
тогда существует такое комплексное
число r, что
,
тогда существует такое комплексное
число r, что
a >22>
= - ra>11>
>22>
= - ra>11>
a>21> = ra>12>
Базис (e>1>, e>2> ) ортонормированный; следовательно
a >11>2
+ a>12>2
= 1
>11>2
+ a>12>2
= 1
|a>22> |2 + |a>21> |2 = 0
тогда | r | = 1.
Р>2 >e>1> = Р>2> ( b>11>g>1> + b>12>g>2>) = b>11>g>1> = b>11>a>11>e>1> + b>11>a>12>e>2>,
Р>2 >e>2> = Р>2> ( b>21>g>1> + b>22>g>2>) = b>21>g>1> = b>21>a>11>e>1> + b>21>a>12>e>2>.
Найдем b>11> и b>21>:
e>1> = b>11>g>1> + b>12>g>2> = b>11> (a>11>e>1> + a>12> e>2>) + b>12 >(a>21>e>1> + a>22>e>2>) = (b>11>a>11> + b>12>a>12>)e>1> + (b>11>a>12> + b>12>a>22>)e>2>,
b >11>a>11>
+ b>12>a>12>
= 1
>11>a>11>
+ b>12>a>12>
= 1
b>11>a>12> + b>12>a>22> = 0 или
b >11>a>11>
+ b>12>a>12>
r = 1
>11>a>11>
+ b>12>a>12>
r = 1
b>11>a>12> - b>12>a>11> r = 0,
Тогда b>11> = a>11>.
Аналогично
E>2> = b>21>g>1> + b>22>g>2> = (b>21>a>11> + b>22>a>21>)e>1> + (b>21>a>12> + b>22>a>22>)e>2>,
b >21>a>11>
+ b>22>a>21>=
0
>21>a>11>
+ b>22>a>21>=
0
b>21>a>12> + b>22>a>22> = 1,
отсюда находим, что b>21> = a>12>.
Тогда матрица оператора Р>2> в базисе {e>1>, e>2> } будет иметь вид (обозначим ее также через Р>2>)
Р>2>
=
 ,
где a>11>>0,
a>12>>0
и a>11>2
+ a>12>2
=1
,
где a>11>>0,
a>12>>0
и a>11>2
+ a>12>2
=1
А)
Пусть a>11>2
= τ, тогда
a>12>2
=1 – τ, a>11>a>12>
=
 .
Так как a>11>a>12>
>0, то τ
.
Так как a>11>a>12>
>0, то τ (0,
1).
(0,
1).
Тогда
Р>2> =
 .
.
В) Положим a>11> = cosφ,тогда a>12> = sinφ и Р>2> запишется следующим образом
Р>2>
=
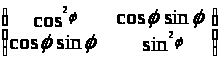 .
.
Найдем коммутант π(P>2>).
Пусть Т =
 оператор перестановочный с Р>1> и
Р>2>, тогда
оператор перестановочный с Р>1> и
Р>2>, тогда
ТР>1> =

 =
=

Р>1>Т =

 =
=

Следовательно b = c = 0.
ТР>2> =
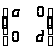
 =
=
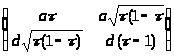
Р>2>Т =

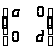 =
=

Следовательно a = d. Тогда Т скалярный оператор и по лемме Шура (теорема 2.6. глава I) представление π неприводимо.
Покажем, что все эти представления неэквивалентны.
Пусть τ, ν (0,
1), τ ≠ ν. Предположим, что
существует унитарный оператор в Н,
устанавливающий эквивалентность. Тогда
(0,
1), τ ≠ ν. Предположим, что
существует унитарный оператор в Н,
устанавливающий эквивалентность. Тогда
UР>1>
= Р>1>U, следовательно
U=
 ,
a, b
,
a, b
 C
C
UР>2>
(τ) =

 =
=

Р>2>
(ν) U
=

 =
=
 .
.
Тогда τ = ν, следовательно U = 0 и представления неэквивалентны.
Теорема 1.1. Пусть π: P>2 >→L(H) - *-представление *-алгебры P>2 >.
Тогда:
(i) Все одномерные и неэквивалентные представления имеют вид: π>0,0>(p>1>) = 0; π>0,0>(p>2>) = 0; π>1,0>(p>1>) = 1; π>1,0>(p>2>) = 0; π>0,1>(p>1>) = 0; π>0,1>(p>2>) = 1; π>1,1>(p>1>) = 1; π>1,1>(p>2>) = 1;
(ii)
Все двумерные неприводимые и неэквивалентные
представления имеют вид: π(p>1>)
 , π(p>2>)
, π(p>2>)
 τ
τ (0, 1).
(0, 1).
Доказательство следует из
сказанного выше и в пункте (ii)
можно положить π(p>2>)
=
 φ
φ (0,
(0,
 ).
).
1.4. n – мерные *-представления *-алгебры P>2 >. Рассмотрим случай нечетной размерности пространства Н. Если dimН=2n+1, где n>1 натуральное, то выполняется неравенство
max (dimН>1>, dimН>1>┴) + max (dimН>2>, dimН>2>┴) > 2n+1 (1.4.)
Тогда обязательно найдутся такие i = 0,1 и j= 0,1, что Н>i>>,>>j>> >≠ {0}, следовательно, существует нетривиальное инвариантное подпространство относительно *-представления π, но тогда π приводимо.
Пусть теперь dimН=2n, n>1 натуральное. Будем считать, что dimН>1> = n, dimН>2> = n и Н>i>>,>>j>> >= {0} для любых i = 0,1 и j= 0,1, то есть Н>i>>,>>j>> > линейно независимы. Если это не так, то снова будет выполнятся неравенство (1.4.) и *-представление π окажется приводимым. При этих условиях справедлива лемма.
Лемма 1.1. Существует х ≠
0, х Н>1>
такой, что Р>1>Р>2>х = λх,
где λ
Н>1>
такой, что Р>1>Р>2>х = λх,
где λ С.
С.
Доказательство. Пусть
 ,
,
 ортонормированный базисы в Н, в
которых матрицы операторов Р>1> и
Р>2> имеют вид
ортонормированный базисы в Н, в
которых матрицы операторов Р>1> и
Р>2> имеют вид
 ,
где I – единичная
матрица порядка n.
Пусть базисы (е) и (g)
связаны уравнениями
,
где I – единичная
матрица порядка n.
Пусть базисы (е) и (g)
связаны уравнениями




к = 1,…, n к = 1,…, n
Так как х Н>1>,
то
Н>1>,
то
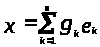 ,
g>k>
,
g>k>
 C,
к = 1,…, n. Тогда
C,
к = 1,…, n. Тогда
Р>1>Р>2>х
= Р>1>Р>2> =
Р>1>Р>2>
=
Р>1>Р>2>
 =
Р>1>
=
Р>1>
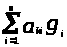 =
=
=
Р>1>

 =
=


 =
=
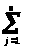 (
(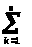
 )
) =
=

Таким образом получаем систему линейных однородных уравнений относительно q>1>,…, q>n>:
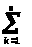

 =
=
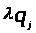
j = 1,…, n
Подбирая λ C
так, чтобы определитель этой системы
обратился в нуль, получим ненулевое
решение q>1>,…,
q>n>.
Это доказывает лемму.
C
так, чтобы определитель этой системы
обратился в нуль, получим ненулевое
решение q>1>,…,
q>n>.
Это доказывает лемму.
Лемма 1.2. Пусть элемент х удовлетворяет условиям леммы 15. Тогда L=л.о. {х, Р>2>х} – инвариантное подпространство в Н относительно Р>1> и Р>2>.
Доказательство. Проверим
инвариантность L. Для
любых a, b
 С
имеем
С
имеем
Р>1>
(aх + bР>2>х)
= aх + λbх
= (a + λb)
х
 L,
L,
Р>2>
(aх + bР>2>х)
= aР>2>х + bР>2>х
= (a + b)
Р>2>> >х
 L
L
dimL = 2, так как Н>i>>,>>j>> >= {0} (для всех i, j= 0,1).
Действительно, если aх
+ bР>2>х = 0,
где, например, а ≠ 0, то х =
 Р>2>х, значит
Р>2>х, значит
 =
0 или 1 и х
=
0 или 1 и х
 Н>1,1>;
тогда Н>1,1>≠{0}.
Н>1,1>;
тогда Н>1,1>≠{0}.
Итак, получаем предложение.
Теорема 1.2. Если dimН
= n, n>2,
то нет неприводимых *-пред-
ставлений
*-алгебры P>2
>. Все неприводимые конечномерные
*-представления одномерны и двумерны.
1.5. Спектральная теорема. Пусть dimН = n. В этом пункте мы получим разложение на неприводимые *-подпредставления исходного *-представления π *-алгебры P>2>, а также разложение пространства Н на инвариантные подпространства относительно π.
Теорема 3.1. (спектральная
теорема). Существует единственное
разложе-
ние Н в ортогональную
сумму инвариантных относительно Р>1>
и Р>2> подпространств
Н = Н>0,0> Н>0,1>
Н>0,1> Н>1,0>
Н>1,0> Н>1,1
>
Н>1,1
>
 (
( (С2
(С2 Н>к>)),
(1.1.)
Н>к>)),
(1.1.)
где
каждому подпространству Н>к>
соответствует одно φ>к> (0,
(0,
 ),
φ>к >≠ φ>i>
при к≠i, dimН>к>
= n>к> (к =
1,…, m). Пусть Р>i>>,>>j>:
Н → Н>i>>,>>j>>
>, Рφ>к>: Н →
С2
),
φ>к >≠ φ>i>
при к≠i, dimН>к>
= n>к> (к =
1,…, m). Пусть Р>i>>,>>j>:
Н → Н>i>>,>>j>>
>, Рφ>к>: Н →
С2 Н>к>
– ортопроекторы к = 1,…, m.
Тогда существуют единственные разложения
операторов
Н>к>
– ортопроекторы к = 1,…, m.
Тогда существуют единственные разложения
операторов
I = P>0,0> P>0,1>
P>0,1> P>1,0 >
P>1,0 >
 P>1,1>
P>1,1> (
( Рφ>к>),
(1.2.)
Рφ>к>),
(1.2.)
P>1>
= P>1,0> P>1,1>
P>1,1> (
( (
(
 I>к>
)) (1.3)
I>к>
)) (1.3)
Р>2>
= P>0,1 >
 P>1,1
>
P>1,1
>
 (
(
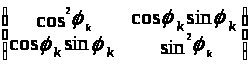
 I>к>
)) (1.4)
I>к>
)) (1.4)
где I>к> – единичный оператор на Н>к> (к = 1,…, m).
Доказательство. Пусть dimН>i>>,>>j> = n>i>>,>>j>. Сразу можем записать разложение
Н = Н>0,0> Н>0,1>
Н>0,1> Н>1,0 >
Н>1,0 >
 Н>1,1
>
Н>1,1
>
 Н΄, где dimН΄ четное
число. Используя лемму 1.2. и теорему 2.1.
главы I можем написать
разложение Н΄ в ортого-
Н΄, где dimН΄ четное
число. Используя лемму 1.2. и теорему 2.1.
главы I можем написать
разложение Н΄ в ортого-
нальную
сумму инвариантных двумерных
подпространств, определяемых параметром
φ>к> (0,
(0,
 ):
):
Н΄ =
 Нφ>к>,
(l = n -
Нφ>к>,
(l = n -
 )
)
Собирая вместе все Нφ>к>, у которых одно φ>к>, получим изоморфизм
Нφ>к> …
… Нφ>к>
≈ С2
Нφ>к>
≈ С2 Н>к>
, где Нφ>к> n>к>
экземпляров, dim(Нφ>к>
Н>к>
, где Нφ>к> n>к>
экземпляров, dim(Нφ>к> …
… Нφ>к>
)=2n>к> dim(С2
Нφ>к>
)=2n>к> dim(С2 Н>к>)
= dimС2 dimН>к>
= 2n>к> .
Следовательно, получаем разложение
(1.1.)
Н>к>)
= dimС2 dimН>к>
= 2n>к> .
Следовательно, получаем разложение
(1.1.)
Н
= Н>0,0>
 Н>0,1>
Н>0,1> Н>1,0 >
Н>1,0 >
 Н>1,1
>
Н>1,1
>
 (
( (С2
(С2 Н>к>))
Н>к>))
Пусть π>i>>,>>j> – сужение π на Н>i>>,>>j>> > ( i, j= 0,1), π>к> – сужение π на Нφ>к> (к = 1,…, m), то есть π>i>>,>>j> и π>к> - *-подпредставления.
Учитывая кратности подпредставлений получаем
π
= n>0,0>π>0,0> n>0,1>π>0,1>
n>0,1>π>0,1> n>1,0>π>1,0>
n>1,0>π>1,0> n>1,1>π>1,1>
n>1,1>π>1,1> (
( n>к>π>к>)
(1.5.)
n>к>π>к>)
(1.5.)
В силу теоремы 2.8. главы I разложения (1.1.) и (1.5.) единственные.
Из (1.1.) следует разложение единичного оператора I (1.2.)
I
= P>0,0>
 P>0,1>
P>0,1> P>1,0 >
P>1,0 >
 P>1,1
>
P>1,1
>
 (
( Рφ>к>)
Рφ>к>)
Тогда ортопроекторы Р>1> и Р>2> примут вид
P>1>
= P>1,0
>
 P>1,1
>
P>1,1
>
 (
( (
(
 I>к>
))
I>к>
))
Р>2>
= P>0,1
>
 P>1,1
>
P>1,1
>
 (
(
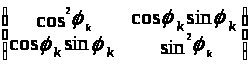
 I>к>
))
I>к>
))
Причем n>1,0>π>1,0>(р>1>) = P>1,0 >, n>0,1>π>0,1>(p>2>) = P>0,1 >, n>1,1>π>1,1>(р>1>) = P>1,1 >, n>0,0>π>0,0>(p>2>) = P>0,0>. В силу теоремы 2.8. главы I разложения I, Р>1> и Р>2> также определяются однозначно.
§ 2. Два ортопроектора в сепарабельном гильбертовом пространстве
2.1. Неприводимые *-представления *-алгебры P>2 >. Пусть А = Р>1> - Р>1>┴ = 2Р>1> – I и В = Р>2> – Р>2>┴ = 2Р>2> – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА = АUА = А2ВА = ВА = U-1, следовательно
UА = АU-1 или АU = U-1А (2.1.)
Лемма 2.1. Операторы А и В неприводимы тогда и только тогда, когда операторы А и U неприводимы.
Доказательство. Допустим, что А
и В неприводимы. Пусть существует
нетривиальное инвариантное подпространство
L относительно операторов
А и U. Тогда UL
= АВL L,
но тогда ВL
L,
но тогда ВL АL
АL L,
то есть пара А, В – приводима.
L,
то есть пара А, В – приводима.
Обратно, пусть А и U
неприводимы. Если операторы А и В
приводимы, то есть
 L
L Н:
АL
Н:
АL L
и ВL
L
и ВL L,
то из включения АВL
L,
то из включения АВL АL
АL L
следует приводимость А и U,
что невозможно.
L
следует приводимость А и U,
что невозможно.
Лемма 2.2. Ортопроекторы Р>1> и Р>2> неприводимы тогда и только тогда, когда А и В неприводимы.
Доказательство. Пусть Р>1>
и Р>2> приводимые операторы, когда
существует нетривиальное инвариантное
подпространство L Н
такое, что Р>1>L
Н
такое, что Р>1>L L,
Р>2>L
L,
Р>2>L L.
Рассмотрим АL = (2Р>1>
– I)L
L.
Рассмотрим АL = (2Р>1>
– I)L L,
ВL = (2Р>2> – I)L
L,
ВL = (2Р>2> – I)L L,
то есть А и В приводимы.
L,
то есть А и В приводимы.
Обратно, пусть А и В приводимые
операторы, тогда Р>1> и Р>2> также
будут приводимы, так как Р>1>L
=
 L
L L,
Р>2>L =
L,
Р>2>L =
 L
L L,
для любого инвариантного относительно
А и В подпространства L в
Н.
L,
для любого инвариантного относительно
А и В подпространства L в
Н.
Лемма 2.3. Если eiφ
 (U),
то e-iφ
(U),
то e-iφ
 (U).
(U).
Доказательство.
1)
Если eiφ
принадлежит точечному спектру оператора
U, то существует f Н:
||f|| = 1 и Uf
= eiφ
f. Тогда по (2.1.) UАf
= АU-1f
= eiφАf,
следовательно, Аf
собственный вектор оператора U,
то есть e-iφ
принадлежит спектру U.
Н:
||f|| = 1 и Uf
= eiφ
f. Тогда по (2.1.) UАf
= АU-1f
= eiφАf,
следовательно, Аf
собственный вектор оператора U,
то есть e-iφ
принадлежит спектру U.
2)
Если eiφ
 (U),
то существует последовательность
единичных векторов
(U),
то существует последовательность
единичных векторов
 в Н || f>n>
|| = 1 такая, что
в Н || f>n>
|| = 1 такая, что
||Uf>n> - eiφf>n> || = || UАf>n> - eiφ A f>n> || = || U-1Аf>n> - eiφ A f>n> || → 0 при n → ∞ (|| Аf>n> || =1)
Тогда
eiφ
 (U-1),
следовательно e-iφ
(U-1),
следовательно e-iφ
 (U).
(U).
Теорема 2.1. Неприводимые пары А и В самосопряженных операторов лишь одномерны и двумерны.
Доказательство. Рассмотрим соотношения
А (U + U-1) = АU + АU-1 = (U-1 +U)А
А (U - U-1) = А (U2 – 2I + U-2) = (U2 – 2I + U-2)А = (U - U-1)2А
Таким образом А (U + U-1) = (U-1 +U)А (2.2.)
А (U - U-1) = (U - U-1)2А (2.3.)
Пара А и U неприводима (лемма 2.1.), тогда по теореме 2.6. главы I имеем
U + U-1 = cI
(U - U-1)2 = d2I
где
c, d
 С.
По теореме преобразования спектров
eiφ+
e-iφ
= c, eiφ-
e-iφ
= ±d.
С.
По теореме преобразования спектров
eiφ+
e-iφ
= c, eiφ-
e-iφ
= ±d.
Если
d = 0, то
 (U)
состоит из одной точки eiφ,
где φ=0 или φ=π, и U
= I или U =
-I. Так как А, U
неприводимая пара, то dimН=1
и А = +I или А = -I.
Поскольку существует одномерное
инвариантное подпространство y
оператора А: л.о. {(A+I)x},
х
(U)
состоит из одной точки eiφ,
где φ=0 или φ=π, и U
= I или U =
-I. Так как А, U
неприводимая пара, то dimН=1
и А = +I или А = -I.
Поскольку существует одномерное
инвариантное подпространство y
оператора А: л.о. {(A+I)x},
х H.
H.
Если
d ≠ 0, то
 (U)
дискретен и состоит из двух точек
eiφ=
(U)
дискретен и состоит из двух точек
eiφ= и e-iφ=
и e-iφ= φ
φ (0,
π)
(0,
π)
Собственное подпространство
оператора U, отвечающее
собственному значению eiφ
(или e-iφ),
Н>ei>>φ>
= {f H
| Uf =
eiφf}
одномерно. Действительно, подпространство,
натянутое на собственные векторы f
и Af
для оператора U: Uf
= eiφf,
U(Аf)
= eiφ
Аf инвариантно
относительно операторов U
и А. U и А неприводимы,
значит dimН>ei>>φ>=
dimН>->>ei>>φ>=1
H
| Uf =
eiφf}
одномерно. Действительно, подпространство,
натянутое на собственные векторы f
и Af
для оператора U: Uf
= eiφf,
U(Аf)
= eiφ
Аf инвариантно
относительно операторов U
и А. U и А неприводимы,
значит dimН>ei>>φ>=
dimН>->>ei>>φ>=1
Таким образом, все неприводимые
пары операторов U и А
такие, что
 (U)
= {eiφ,
e-iφ}
φ
(U)
= {eiφ,
e-iφ}
φ (0,
π) в базисе из собственных
векторов оператора U имеют
вид:
(0,
π) в базисе из собственных
векторов оператора U имеют
вид:
А
=
 ,
U
=
,
U
=
 ,
В =
,
В =

Теорема 2.2. Неприводимые пары
Р>1>, Р>2 > ортопроекторов лишь
одномер-
ны и двумерны.
Доказательство. Сразу следует из леммы 2.2.
2.2. Спектральная теорема. Пусть Н – сепарабельное гильбертово пространство, тогда справедлива следующая теорема.
Теорема 2.3. (спектральная теорема в форме операторов умножения). Паре ортопроекторов Р>1> и Р>2>> > в сепарабельном гильбертовом пространстве Н соответствует разложение
Н = Н>0,0> Н>0,1>
Н>0,1> Н>1,0
>
Н>1,0
>
 Н>1,1>
Н>1,1> (
( (С2
(С2 L>2>((0,
L>2>((0,
 ),
dρ>к>)))
(2.4.)
),
dρ>к>)))
(2.4.)
где
ρ>1 >> ρ>2> >… ρ>к>
меры на интервале (0,
 ),
такое, что имеют место равенства
),
такое, что имеют место равенства
P>1>
= P>1,0
>
 P>1,1
>
P>1,1
>
 (
( (
(
 I>к>
))
(2.5.)
I>к>
))
(2.5.)
Р>2>
= P>0,1
>
 P>1,1>
P>1,1> (
(
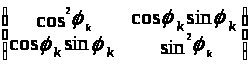
 I>к>
))
(2.6.)
I>к>
))
(2.6.)
I>к>
– единичный оператор в L>2>((0,
 ),
dρ>к>)
),
dρ>к>)
Доказательство. Пространство Н можно представить в виде ортогональной суммы инвариантных подпространств
Н = Н>0,0>
 Н>0,1>
Н>0,1> Н>1,0 >
Н>1,0 >
 Н>1,1
>
Н>1,1
>
 Н΄, то есть отщепить все одномерные
представления от исходного. Н΄ состоит
из инвариантных двумерных подпространств.
Н΄, то есть отщепить все одномерные
представления от исходного. Н΄ состоит
из инвариантных двумерных подпространств.
Всякому положительному функционалу F в *-алгебре P>2 > отвечает циклическое представление π>F> *-алгебры P>2 > в некотором гильбертовом пространстве Н>F>. При этом Н>F> можно реализовать как L>2>(F), то есть как гильбертово пространство всех функций с интегрируемым квадратом по мере μ>F> на Т.
Пусть каждому вектору ξ Н
поставим в соответствие подпространство
Н>ξ>> >
Н
поставим в соответствие подпространство
Н>ξ>> >
 Н, которое получается замыканием
множества векторов вида π(х)ξ,
где х
Н, которое получается замыканием
множества векторов вида π(х)ξ,
где х А.
Ограничения операторов из π(А)
на Н>ξ>>
> является циклическим представлением.
Обозначим его через π>ξ>,
а соответствующую меру на Т через
μ>ξ>. Введем упорядочение
в Н, полагая ξ>η, если
μ>ξ>> >>
μ>η> (то есть μ>η> абсолютно
непрерывна по мере μ>ξ>).
А.
Ограничения операторов из π(А)
на Н>ξ>>
> является циклическим представлением.
Обозначим его через π>ξ>,
а соответствующую меру на Т через
μ>ξ>. Введем упорядочение
в Н, полагая ξ>η, если
μ>ξ>> >>
μ>η> (то есть μ>η> абсолютно
непрерывна по мере μ>ξ>).
Если η Н>ξ>,
то Н>η>
Н>ξ>,
то Н>η> Н>ξ>,
тогда π>η> – циклическое
подпредставление π>ξ>.
Пусть Е
Н>ξ>,
тогда π>η> – циклическое
подпредставление π>ξ>.
Пусть Е Т и μ>ξ>> >(Е)
= 0, тогда μ>η>> >(Е) = 0,
следовательно μ>ξ>>
>> μ>η>, а значит ξ>η.
Т и μ>ξ>> >(Е)
= 0, тогда μ>η>> >(Е) = 0,
следовательно μ>ξ>>
>> μ>η>, а значит ξ>η.
Множество максимальных векторов
всюду плотно в Н. Пусть существует
счетное разложение Н =
 Нη>к>.
Пусть {ζ>i>} –
последовательность, в которой каждый
из векторов η>i>
встречается бесконечное число раз.
Определим ξ>к>
индуктивно, так, чтобы выполнялись
условия:
Нη>к>.
Пусть {ζ>i>} –
последовательность, в которой каждый
из векторов η>i>
встречается бесконечное число раз.
Определим ξ>к>
индуктивно, так, чтобы выполнялись
условия:
ξ>к+1>
– максимальный вектор в ( Нξ>i>)┴,
Нξ>i>)┴,
d
(ζ>к>,
 Нξ>i>)
≤
Нξ>i>)
≤
 .
.
Тогда
разложение Н =
 Нξ>к>
такое что ξ>к>>ξ>к+1>
и μ>к>>μ>к+1 >.
Нξ>к>
такое что ξ>к>>ξ>к+1>
и μ>к>>μ>к+1 >.
Пусть представления π>μ>
в L>2>(Т, μ) и π>ν
>в L>2>(Т, ν) эквивалентны.
Пусть v:L>2>(Т,
μ) →L>2>(Т, ν) устанавливающий
их эквивалентность изоморфизм. Положим
f=1, а=v(f),
тогда для любой непрерывной функции g
на Т v(g)=vπ>μ>(g)f
= π>ν >(g)vf
= π>ν >(g)a
= ga.
Так как v – изометрическое
отображение, то dμ=|a|2dν.
Таким образом мера μ абсолютно непрерывна
по мере ν. Аналогично, рассматривая
обратный оператор, получаем, что ν
абсолютно непрерывна по μ, то есть эти
меры эквивалентны. Значит существует
разложение Н΄ =
 (С2
(С2 L>2>(Т,
μ>к>)), где μ>1>>μ>2>>…
и соответствующие этим мерам представления
неприводимы и неэквивалентны. Это
доказывает равенство (2.4.). Тогда из
(2.4.) следуют формулы:
L>2>(Т,
μ>к>)), где μ>1>>μ>2>>…
и соответствующие этим мерам представления
неприводимы и неэквивалентны. Это
доказывает равенство (2.4.). Тогда из
(2.4.) следуют формулы:
P>1>
= P>1,0
>
 P>1,1
>
P>1,1
>
 (
( (
(
 I>к>
))
I>к>
))
Р>2>
= P>0,1
>
 P>1,1>
P>1,1> (
(
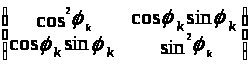
 I>к>
))
I>к>
))
I>к>
– единичный оператор в L>2>((0,
 ),
dρ>к>).
),
dρ>к>).
Теорема 2.4. (спектральная теорема в форме разложения единицы). Паре ортопроекторов Р>1> и Р>2>> > в сепарабельном гильбертовом пространстве Н соответствует разложение
Н = Н>0,0> Н>0,1>
Н>0,1> Н>1,0
>
Н>1,0
>
 Н>1,1>
Н>1,1>
 С2
С2 Н(φ)dЕ(φ)
(2.7.)
Н(φ)dЕ(φ)
(2.7.)
в
прямой интеграл инвариантных относительно
Р>1>, Р>2> подпространств и
определенное на Т = (0,
 )
разложение dЕ(φ) единичного
оператора I>+>=E(0,
)
разложение dЕ(φ) единичного
оператора I>+>=E(0,
 )
в Н>+> =
)
в Н>+> = С2
С2 Н(φ)dЕ(φ),
такое что имеет место равенство
Н(φ)dЕ(φ),
такое что имеет место равенство
P>1>
= P>1,0
>
 P>1,1
>
P>1,1
>


 I>+>
(2.8.)
I>+>
(2.8.)
Р>2>
= P>0,1
>
 P>1,1>
P>1,1>


 dЕ(φ)
(2.9.)
dЕ(φ)
(2.9.)
Доказательство. Всякий
самосопряженный оператор А, действующий
в Н, изометрически изоморфен оператору
умножения на независимую переменную в
пространстве
 L>2>(R,
dρ>к>), где
ρ>к> зависит от разложения
единицы оператора А. Тогда доказательство
спектральной теоремы в форме разложения
единицы следует непосредственно из
спектральной теоремы в форме операторов
умножения.
L>2>(R,
dρ>к>), где
ρ>к> зависит от разложения
единицы оператора А. Тогда доказательство
спектральной теоремы в форме разложения
единицы следует непосредственно из
спектральной теоремы в форме операторов
умножения.
Глава III. Спектр суммы двух ортопроекторов
§1. Спектр суммы двух ортопроекторов в унитарном пространстве
1.1. Спектр ортопроектора в гильбертовом пространстве.
Теорема 1.1. Пусть Н –
гильбертово пространство. Если Р –
ортопроектор, то
 (Р)
=
(Р)
=
 >р>
(Р) = {0, 1}, где
>р>
(Р) = {0, 1}, где
 >р>
(Р) – точечный спектр при условии, что
Р ≠ 0 и Р ≠ I.
>р>
(Р) – точечный спектр при условии, что
Р ≠ 0 и Р ≠ I.
Доказательство. Рассмотрим
выражение Рх - λх = y,
х, y Н, λ
Н, λ С. Тогда (1 - λ) Р>х> = Р>y>
. Если λ ≠ 1, то Р>х> =
С. Тогда (1 - λ) Р>х> = Р>y>
. Если λ ≠ 1, то Р>х> =
 Р>y>.
Если х ≠ 1, то х =
Р>y>.
Если х ≠ 1, то х =
 (
( Р>y>
- y), тогда
Р>y>
- y), тогда
 (Р)
= {0, 1}.
(Р)
= {0, 1}.
Так
как Р ≠ 0 и Р ≠ I, то
существует х ≠ 0 такой, что Р>х>
≠ 0. Тогда Р(Р>х>) = Р>х>, то есть
1
 >р>
(Р). Существует y ≠
0: (I - Р)y
≠ 0, тогда Р(I - Р)y
= 0 = 0 · (I - Р)y,
то есть 0
>р>
(Р). Существует y ≠
0: (I - Р)y
≠ 0, тогда Р(I - Р)y
= 0 = 0 · (I - Р)y,
то есть 0

 >р>
(Р). Итак,
>р>
(Р). Итак,
 (Р)
=
(Р)
=
 >р>
(Р) = {0, 1}.
>р>
(Р) = {0, 1}.
1.2. Постановка задачи. Пусть заданы два ортопроектора Р>1> и Р>2> в унитарном пространстве Н. Тогда мы знаем спектр каждого из них. Найдем спектр суммы Р>1> + Р>2> в неприводимых представлениях.
1.3. Спектр в одномерном
пространстве. Пусть dimH
=1. Пусть, как и выше, Н>к> –
область значений оператора Р>к> к
= 1,2. Обозначим через А = Р>1> + Р>2>
и найдем
 (А).
(А).
1)
Р>1> = Р>2> = 0, то для любого х Н Ах = 0 или Ах = 0 · х, то
есть 0
Н Ах = 0 или Ах = 0 · х, то
есть 0

 (А).
(А).
2)
Р>1> = 0, Р>2> = I, то
для любого х Н>2> = Н Ах = х, то
есть 1
Н>2> = Н Ах = х, то
есть 1

 (А).
(А).
3)
Р>1> = I, Р>2> = 0, то
для любого х Н>1> = Н Ах = х.
Н>1> = Н Ах = х.
4)
Р>1> = Р>2> = I,
то для любого х Н>1> = Н>2> = Н Ах
= Р>1>х + Р>2>х = 2х, то
есть 2
Н>1> = Н>2> = Н Ах
= Р>1>х + Р>2>х = 2х, то
есть 2

 (А).
(А).
Таким образом, если dimH
=1, то
 (А)
(А)
 {0,
1, 2}.
{0,
1, 2}.
1.4. Спектр в двумерном пространстве. Пусть dimH =2. Сохраним обозначения (1.1.) Главы II.
1)
х Н>0,0>> >, тогда Ах = 0 и
0
Н>0,0>> >, тогда Ах = 0 и
0

 (А).
(А).
2)
х Н>0,1>> > или х
Н>0,1>> > или х Н>1,0>> >, тогда Ах = х
и 1
Н>1,0>> >, тогда Ах = х
и 1

 (А).
(А).
3)
х Н>1,1>, тогда Ах = 2х, то есть
2
Н>1,1>, тогда Ах = 2х, то есть
2

 (А).
(А).
Если существуют i,
j= 0,1 такие, что Н>i>>,>>j>>
> ≠ {0}, то существуют k,l
= 0,1 такие, что Н>i>>,>>j>>
>
 Н>k>>,>>l>
= H. > >В этом случае
Н>k>>,>>l>
= H. > >В этом случае
 (А)
(А)
 {0,
1, 2}.
{0,
1, 2}.
Пусть теперь Н>k>>,>>l>
= {0} для любых k,l
= 0,1. Допустим, что существует одномерное
инвариантное подпространство L
относительно Р>1> и Р>2>, тогда
АL L.
Пусть х
L.
Пусть х L, тогда Р>k>х
= λ>к>х (k
= 1, 2 ). Так как Р>k>>
> ортопроектор, то возможны случаи:
L, тогда Р>k>х
= λ>к>х (k
= 1, 2 ). Так как Р>k>>
> ортопроектор, то возможны случаи:
λ>1> = 0, λ>2> = 0;
λ>1> = 0, λ>2> = 1;
λ>1> = 1, λ>2> = 0;
λ>1> = 1, λ>2> = 1;
Но это означает, что
 k,l
= 0,1 такие, что Н>k>>,>>l>
≠ {0} вопреки предположению. Тогда пара
Р>1>, Р>2> неприводима. Значит
мы можем записать матрицы операторов
Р>1> и Р>2 >в некотором
ортонормированном базисе, согласно
теореме 1.1. главы II.
k,l
= 0,1 такие, что Н>k>>,>>l>
≠ {0} вопреки предположению. Тогда пара
Р>1>, Р>2> неприводима. Значит
мы можем записать матрицы операторов
Р>1> и Р>2 >в некотором
ортонормированном базисе, согласно
теореме 1.1. главы II.
Р>1> =
 ,
Р>2>
,
Р>2>
 τ
τ (0, 1)
(0, 1)
Найдем спектр линейной комбинации
ортопроекторов aР>1>
+ bР>2>, a
и b С. Для этого решим характеристическое
уравнение det(aР>1>
+ bР>2> – λI)
= 0.
С. Для этого решим характеристическое
уравнение det(aР>1>
+ bР>2> – λI)
= 0.
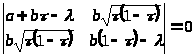
 (1.1.)
(1.1.)
Тогда
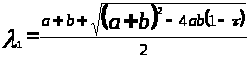 ,
,
 (1.2)
(1.2)
Положим a =
1, b =1, ε =
 ,
тогда λ>1> = 1+ε , λ>2>
= 1-ε и 0<ε<1
(поскольку 0<τ<1.
,
тогда λ>1> = 1+ε , λ>2>
= 1-ε и 0<ε<1
(поскольку 0<τ<1.
Тогда
 (А)
(А)
 {0,
1, 2}
{0,
1, 2} {1+ε
, 1-ε}. Причем собственные
значения 1+ε и 1-ε входят
в спектр А одновременно.
{1+ε
, 1-ε}. Причем собственные
значения 1+ε и 1-ε входят
в спектр А одновременно.
1.5. Спектр в n-мерном
пространстве. Пусть dimH
=n. Если Н =К L,
где К, L инвариантные
подпространства относительно оператора
А, то для любого х
L,
где К, L инвариантные
подпространства относительно оператора
А, то для любого х Н существует единственное разложение
x = k
+l, k
Н существует единственное разложение
x = k
+l, k K, l
K, l L. Пусть λ
L. Пусть λ
 (А), тогда Ах = λх =λk
+λl;, следовательно,
если пространство Н разложено в
ортогональную сумму инвариантных
подпространств, то спектр оператора А
можно найти как объединение спектров
сужений оператора А на соответствующие
инвариантные подпространства.
(А), тогда Ах = λх =λk
+λl;, следовательно,
если пространство Н разложено в
ортогональную сумму инвариантных
подпространств, то спектр оператора А
можно найти как объединение спектров
сужений оператора А на соответствующие
инвариантные подпространства.
Используя лемму 1.2. главы II,
представим Н в виде ортогональной
суммы подпространств Н>0>>
>= Н>0,0>, Н>1>=Н>0,1> Н>1,0>,
Н>2>=Н>1,1> и
двумерных, инвариантных относительно
А, подпространств Нφ>к>
φ>к>
Н>1,0>,
Н>2>=Н>1,1> и
двумерных, инвариантных относительно
А, подпространств Нφ>к>
φ>к> (0,
(0,
 ),
(к = 1,…, s). При этом
операторы Р>1> и Р>2> неприводимы
в Нφ>к> (к = 1,…, s),
и собственные значения 1+ε>к>,
1-ε>к> входят одновременно
в спектр А. Так как А*=А, то соответствующие
собственные векторы ортогональны. Тогда
имеет место разложение на собственные
подпространства
),
(к = 1,…, s). При этом
операторы Р>1> и Р>2> неприводимы
в Нφ>к> (к = 1,…, s),
и собственные значения 1+ε>к>,
1-ε>к> входят одновременно
в спектр А. Так как А*=А, то соответствующие
собственные векторы ортогональны. Тогда
имеет место разложение на собственные
подпространства
Нφ>к> = Н>1+>>ε>>к>>
>
 Н>1->>ε>>к>>
>, причем dimН>1+>>ε>>к>>
>= dimН>1->>ε>>к>>
>= 1 (1.3)
Н>1->>ε>>к>>
>, причем dimН>1+>>ε>>к>>
>= dimН>1->>ε>>к>>
>= 1 (1.3)
Если φ>к >≠ φ>i>,
то ε>к >≠ ε>i>
(так как ε>к> =
 =cosφ>к
> и φ>к>
=cosφ>к
> и φ>к> (0,
(0,
 )).
Объединим все Нφ>к> , у
которых одинаковые φ>к >, в
одно слагаемое, и обозначим его через
Нφ>к>. При этом, если
dimНφ>к> =
2q>k>,
то есть Нφ>к> состоит
из q>k>
экземпляров двумерных подпространств,
отвечающих одному φ>к >, то
объединяя вместе все соответствующие
одномерные собственные подпространства,
получим Нφ>к> = Н>1+>>ε>>к>>
>
)).
Объединим все Нφ>к> , у
которых одинаковые φ>к >, в
одно слагаемое, и обозначим его через
Нφ>к>. При этом, если
dimНφ>к> =
2q>k>,
то есть Нφ>к> состоит
из q>k>
экземпляров двумерных подпространств,
отвечающих одному φ>к >, то
объединяя вместе все соответствующие
одномерные собственные подпространства,
получим Нφ>к> = Н>1+>>ε>>к>>
>
 Н>1->>ε>>к>>
>, dimН>1+>>ε>>к>>
>= dimН>1->>ε>>к>>
>= q>k>.
Н>1->>ε>>к>>
>, dimН>1+>>ε>>к>>
>= dimН>1->>ε>>к>>
>= q>k>.
Теорема 1.2. Самосопряженный оператор А представим в виде суммы двух ортопроекторов А = Р>1> и Р>2> тогда и только тогда, когда
 (А)
(А)
 {0,
1, 2}
{0,
1, 2} (
( {1+ε
, 1-ε}), 0<ε>к><1,
{1+ε
, 1-ε}), 0<ε>к><1,
причем dimН>1+>>ε>>к>> >= dimН>1->>ε>>к>> >к = 1,…, m.
Доказательство. Пусть А = Р>1> и Р>2>, тогда его спектр был найден выше:
 (А)
(А)
 {0,
1, 2}
{0,
1, 2} (
( {1+ε
, 1-ε}), где 0<ε>к><1для
любого к = 1,…, m.
{1+ε
, 1-ε}), где 0<ε>к><1для
любого к = 1,…, m.
Обратно, пусть нам известен спектр оператора А и известно, что размерности соответствующих собственных подпространств совпадают, то есть
dimН>1+>>ε>>к>> >= dimН>1->>ε>>к>> >. Существует единственное разложение Н в ортогональную сумму инвариантных подпространств ((1.1.) Глава II):
Н
= Н>(0)> Н>(1) >
Н>(1) >
 Н>(2)>
Н>(2)> (
( (С2
(С2 Н>к>))
(1.4.)
Н>к>))
(1.4.)
(1.4.) можно записать иначе
Н
= Н>(0)> Н>(1) >
Н>(1) >
 Н>(2)>
Н>(2)> (
( (С2
(С2 (Н>1+>>ε>>к>>
>
(Н>1+>>ε>>к>>
>
 Н>1->>ε>>к>>
>))) (1.5.)
Н>1->>ε>>к>>
>))) (1.5.)
Зададим ортопроекторы Р>1> и Р>2> следующим образом
P>1>
= P>Н>>2> (
( (
(
 I>к>
))
(1.6.)
I>к>
))
(1.6.)
Р>2>
= P>Н>>1>>
>
 P>Н>>2>>
>
P>Н>>2>>
>
 (
(
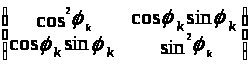
 I>к>
)) (1.7.)
I>к>
)) (1.7.)
где P>Н>>к> – ортопроектор в Н на Н>(к)> (к = 1, 2), I>s> – единичный оператор в H>s> s=1,…, m. Но тогда
Р>1>
+ Р>2> = P>Н>>1>>
>
 P>Н>>2>>
>
P>Н>>2>>
>
 (
(

 I>к>
)) = А, при этом А = А*
I>к>
)) = А, при этом А = А*
1.6. Линейная комбинация ортопроекторов. Пусть теперь с. Из (1.2.) следует λ>1> + λ>2> = a + b. Пусть λ>2> = ε, тогда λ>1> = a + b – ε.
Оценим ε. Заметим, что (a +b)2 – 4ab(1-τ) = (a - b)2 + 4abτ > 0.
Тогда
ε =
 >
>
 =
0, то есть ε = 0.
=
0, то есть ε = 0.
Допустим, что ε ≥ a , тогда
a
≤

 ≤
b – a
≤
b – a
(b - a)2 +4abτ ≤ (b – a)2
abτ ≤ 0, но abτ > 0 и значит ε < a
Итак,
λ >1>
= ε
>1>
= ε
λ>2> = a + b – ε. (1.8.)
0 < ε < a
Пусть dimH =n. Тогда справедлива теорема.
Теорема 1.3. Самосопряженный оператор А представим в виде линейной комбинации ортопроекоров А = aР>1> + bР>2>, 0<a<b тогда и только тогда, когда
 (А)
(А)
 {0,
a, b,
a +
b}
{0,
a, b,
a +
b} (
( {ε>к>>
>, a +
b - ε>к>}),
0<ε>к><1,
и
{ε>к>>
>, a +
b - ε>к>}),
0<ε>к><1,
и
dimН>ε>>к>> >= dimН>a>>+>>b>>->>ε>>к>> >(Н>ε>>к>> >, Н>a>>+>>b>>->>ε>>к>> >- собственные подпространства оператора А, отвечающие ε>к>) к=1,…m.
Доказательство. Пусть А = aР>1>
+ bР>2>, 0<a<b.
Найдем
 (А).
(А).
1)
х Н>0,0>, то Ах = 0 и 0
Н>0,0>, то Ах = 0 и 0
 (А);
(А);
2)
х Н>0,1>> >, то Ах = bx
и b
Н>0,1>> >, то Ах = bx
и b
 (А);
(А);
3)
х Н>1,0>> >, то Ах = ax
и a
Н>1,0>> >, то Ах = ax
и a
 (А);
(А);
4)
х Н>1,1>> >, то Ах = (a+b)x
и a+b
Н>1,1>> >, то Ах = (a+b)x
и a+b
 (А).
(А).
Тогда
 (А)
(А)
 {0,
a, b,
a + b}
{0,
a, b,
a + b} (
( {ε>к
>, a + b
- ε>к>}), где 0<ε>к><1,
к=1,…m. Причем числа
ε>к>, a
+ b - ε>к>
входят одновременно в спектр А, и
соответству-
{ε>к
>, a + b
- ε>к>}), где 0<ε>к><1,
к=1,…m. Причем числа
ε>к>, a
+ b - ε>к>
входят одновременно в спектр А, и
соответству-
ющие собственные
подпространства ортогональны и одномерны,
так как А=А*. Тогда сумма всех собственных
подпространств, отвечающих одному ε>к>
также инвариантна относительно А и
dimН>ε>>к>>
>= dimН>a>>+>>b>>->>ε>>к>>
>= q>k>.
(с учетом кратности ε>к>)
Обратно. Существует единственное разложение Н в силу (1.4.)
Н = Н>(0)> Н>(>>a>>)
>
Н>(>>a>>)
>
 Н>(>>b>>)>
Н>(>>b>>)> Н>(>>a>>+>>b>>)>
Н>(>>a>>+>>b>>)> (
( (С2
(С2 Н>к>))
(1.9.)
Н>к>))
(1.9.)
Где Н>(0)>=Н>0,0>> >, Н>(>>a>>) >=Н>1,0>> >, Н>(>>b>>)>=Н>0,1>> >, Н>(>>a>>+>>b>>)>=Н>1,1>> > или
Н
= Н>(0)> Н>(>>a>>)
>
Н>(>>a>>)
>
 Н>(>>b>>)>
Н>(>>b>>)> Н>(>>a>>+>>b>>)>
Н>(>>a>>+>>b>>)> (
( (Н>ε>>к>
(Н>ε>>к> Н>a>>+>>b>>->>ε>>к>)
(1.10.)
Н>a>>+>>b>>->>ε>>к>)
(1.10.)
Положим
P>1>
= P>a> P>a+b
>
P>a+b
>
 (
( (
(
 I>к>
))
(1.11.)
I>к>
))
(1.11.)
Р>2>
= P>b
>
 P>a+b
>
P>a+b
>
 (
(
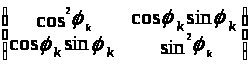
 I>к>
)) (1.12.)
I>к>
)) (1.12.)
Но тогда
aР>1>
+ bР>2>
= aP>a> bP>b
>
bP>b
>
 (а+b)P>a+b
>
(а+b)P>a+b
>
 (a
(a (
(
 I>к>
))
I>к>
))
 (b
(b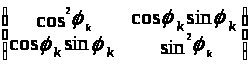
 I>к>
)) = A.
I>к>
)) = A.
Спектр оператора А совпадает с
{0, a, b,
a + b} (
( {ε>к
>, a + b
- ε>к>}), (0<ε>к><1,
к=1,…m) по построению
и А = А* как вещественная комбинация
ортопроекторов.
{ε>к
>, a + b
- ε>к>}), (0<ε>к><1,
к=1,…m) по построению
и А = А* как вещественная комбинация
ортопроекторов.
§ 2. Спектр суммы двух ортопроекторов в сепарабельном гильбертовом пространстве
2.1. Спектр оператора А = Р>1> + Р>2>. Изучим оператор Р>1> + Р>2> в сепарабельном гильбертовом пространстве.
Теорема 2.1. Самосопряженный
оператор А представим в виде суммы двух
ортопроекторов А = Р>1> + Р>2>
тогда и только тогда, когда
 (А)
= [0, 2] и пространство Н можно разложить
в ортогональную сумму инвариантных
относительно А пространств
(А)
= [0, 2] и пространство Н можно разложить
в ортогональную сумму инвариантных
относительно А пространств
Н
= Н>0>
 Н>1>
Н>1> Н>2 >
Н>2 >
 (
( (С2
(С2 L>2>((0,
L>2>((0,
 ),
dρ>к>)))
(2.1.)
),
dρ>к>)))
(2.1.)
и меры ρ>к> инвариантны относительно преобразования 1+х → 1-х.
Доказательство. Пусть А = Р>1>
+ Р>2>. Н>0>=Н>0,0>>
>, Н>1>=Н>1,0> Н>0,1>>
>, Н>2>=Н>1,1>>
>
Н>0,1>>
>, Н>2>=Н>1,1>>
>
Поставим
в соответствие φ→ε cosφ,
где φ (0,
(0,
 ).
Тогда, как было найдено выше, спектр
).
Тогда, как было найдено выше, спектр
 (А)
(А)
 [0, 2] и Н можно разложить (опираясь
на спектральную теореме 2.3. главы II)
в ортогональную сумму (2.1.)
[0, 2] и Н можно разложить (опираясь
на спектральную теореме 2.3. главы II)
в ортогональную сумму (2.1.)
Н
= Н>0>
 Н>1>
Н>1> Н>2 >
Н>2 >
 (
( (С2
(С2 L>2>((0,
2), dρ>к>)))
L>2>((0,
2), dρ>к>)))
Поскольку собственные подпространства, соответствующие собственным значениям А 1+ε , 1-ε, 0<ε<1 входят одновременно в спектр и их значения совпадают, то каждая мера ρ>к>> > (к = 1, 2, …) должна быть инвариантной относительно преобразования 1 + х → 1- х.
Обратно. Пусть имеет место (2.1.)
и
 (А)
(А)
 [0, 2]. Тогда зададим ортопроекторы Р>1>΄
Р>2>΄ равенствами
[0, 2]. Тогда зададим ортопроекторы Р>1>΄
Р>2>΄ равенствами
Р>1>΄
= P>1 >P>2
>P>2 >(
>( (
(
 I>к>
))
I>к>
))
Р>2>΄
= P>2
 >
(
>
(
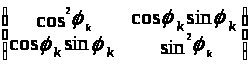
 I>к>
))
I>к>
))
где P>i>: Н→Н>i> (i = 0, 1, 2) ортопроектор, I>k> – единичный оператор в L>2>((0, 2), dρ>к>)). Тогда А =Р>1>΄ + Р>2>΄ - самосопряженный оператор, спектр которого содержится в [0, 2], так как Р>к>΄ (к = 1, 2) является суммой ортопроекторов на взаимно ортогональные пространства.
2.2. Спектр линейной комбинации А = aР>1> + bР>2> (0<a<b). Рассмотрим теперь случай, когда А = aР>1> + bР>2> (0<a<b).
Теорема 2.2. Самосопряженный
оператор А представим в виде линейной
комбинации двух ортопроекторов А = aР>1>
+ bР>2>, 0<a<b
тогда и только тогда, когда
 (А)
(А)
 [0, a]
[0, a]
 [b,
a+b]
и Н можно представить в виде
ортогональной суммы инвариантных
относительно А пространств
[b,
a+b]
и Н можно представить в виде
ортогональной суммы инвариантных
относительно А пространств
Н
= Н>0> Н>a>> >
Н>a>> >
 Н>b>
Н>b> Н>a>>+>>b>
Н>a>>+>>b> (
( (С2
(С2 L>2>([0,
a]
L>2>([0,
a]
 [b,
a+b],
dρ>к>))))
(2.2.)
[b,
a+b],
dρ>к>))))
(2.2.)
и меры ρ>к> инвариантны относительно преобразования х→a+b.
Доказательство. Пусть А = aР>1>
+ bР>2> (0<a<b).
Пусть Н>0>=Н>0,0>,
Н>а>=Н>0,1>,
Н>b>=Н>1,0>>
>, Н>a>>+>>b>=Н>1,1>.
Так как
 (А)
(А)
 [0, a]
[0, a]
 [b,
a+b]
и собственные подпространства, отвечающие
собственным значениям оператора А
входят в Н одновременно (причем их
размерности совпадают) то аналогично
теореме 2.1. получаем
[b,
a+b]
и собственные подпространства, отвечающие
собственным значениям оператора А
входят в Н одновременно (причем их
размерности совпадают) то аналогично
теореме 2.1. получаем
Н
= Н>0> Н>a>> >
Н>a>> >
 Н>b>
Н>b> Н>a>>+>>b>
Н>a>>+>>b> (
( (С2
(С2 L>2>([0,
a]
L>2>([0,
a]
 [b,
a+b],
dρ>к>))))
[b,
a+b],
dρ>к>))))
где меры ρ>к> (к = 1, 2, …) инвариантны относительно преобразования х → a+b-х.
Обратно, пусть
 (А)
(А)
 [0, a]
[0, a]
 [b,
a+b]
и имеется разложение Н (2.2.). Тогда зададим
Р>1> и Р>2> следующим образом
[b,
a+b]
и имеется разложение Н (2.2.). Тогда зададим
Р>1> и Р>2> следующим образом
P>1>
= P>a> P>a+b
>
P>a+b
>
 (
( (
(
 I>к>
))
I>к>
))
Р>2>
= P>b
>
 P>a+b
>(
P>a+b
>(
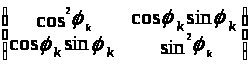
 I>к>
))
I>к>
))
где
Р>α>: Н→Н>α>
, α = a,
b, a+b
– ортопроекторы, I>к>
– единичный оператор в L>2>([0,a]
 [b,
a+b]).
Тогда
[b,
a+b]).
Тогда
А
= aР>1>
+ bР>2>
= aР>1> bР>2>
bР>2> (a+b)P>a+b
>
(a+b)P>a+b
>
 (
( (
(
 I>к>
))
I>к>
))

 (
(
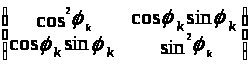
 I>к>
))
I>к>
))
ЗАКЛЮЧЕНИЕ
В дипломной работе изучена пара ортопроекторов в сепарабельном гильбертовом пространстве Н, приведено описание всех неприводимых и неэквивалентные *-представления *-алгебры P>2 >.
P>2 >= С <p>1>, p>2> | p>к>2 = p>к>* =p>к>>.
А именно: 4 одномерных π>0,0>(p>1>) = 0, π>0,0>(p>2>) = 0; π>0,1>(p>1>) = 0, π>0,1>(p>2>) = 1; π>1,0>(p>1>) = 1, π>1,0>(p>2>) = 0; π>1,1>(p>1>) = 1, π>1,1>(p>2>) = 1.
И двумерные:
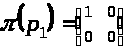 ,
,
 τ
τ (0, 1)
(0, 1)
Изучен спектр операторов Р>1> + Р>2>, aР>1> + bР>2> (0<a<b), а также необходимые и достаточные условия представимости самосопряженного оператора А в виде А = Р>1> + Р>2 > и А = aР>1> + bР>2> (0<a<b).
ЛИТЕРАТУРА
Ахиезер Н.И., Глазман И.М. Теория линейных операторов в гильбертовом пространстве, М., Наука, 1966.
Березенский Ю.М., Ус Г.Ф., Шефтель З.Г. Функциональный анализ, К., Выща школа, 1990.
Браттели У., Робинсон Д. Операторные алгебры и квантовая статистическая механика: С*- W* -алгебры. Группы симметрий. Разложение состояний., М., Мир, 1982.
Диксмье Ж. С*-алгебры и их представления. М., Наука, 1974.
Кириллов А.А. Элементы теории представлений. М., Наука, 1978.
Кужель А.В. Алгебры конечного ранга, С. СГУ, 1979.
Ленг С. Алгебра. М., Мир, 1968.
Мерфи Д. С*-алгебры и теория операторов. М., Мир, 1998.
Наймарк М.А. Нормированные кольца. М., Гостехиздат, 1956.
Рудин У. Функциональный анализ. М., Мир, 1975.
NishioK, Linear algebra and its applications 66: 169-176, Elsevier Science Publishing Co., Inc., 1985.
Samoilenko Y.S., Representation theory of algebras, Springer, 1998.