Типовой расчет графов

Типовой расчет графов

Данная работа является типовым расчетом N2 по курсу "Дискретная математика" по теме "Графы", предлагаемая студентам МГТУ им. Баумана. (Вариант N 17).

Сразу хочу сказать для своих коллег: Граждане! Имейте терпение и совесть, поймите, что я это делаю для Вас с целью помочь разобраться в этой теме, а не просто свалить очередной предмет. Мне известно, как непросто сейчас с литературой, и с информацией вообще. Поиски неизвестно какой книги занимают много времени, поэтому в конце я привел небольшой список литературы, составленный мной из различных источников в дополнение к списку, написанному ранее в работе по графам (о постановке лаб. работ по алгоритму Прима и Дейкстра), которая, я надеюсь, есть в сети.

Содержание работы:

Типовой расчет состоит из 11-ти задач:

1, 2 и 3 задачи относятся к способам задания графов и опредению их характеристик, таких как диаметр, радиус и т.д.

4 и 5 задачи соответственно на алгоритм Прима и Дейкстра. Здесь я снова отсылаю Вас к более ранней работе (см. выше).

6-я задача о поиске максим ального потока в сети (метод Форда-Фалкерсона).

7-я задача - Эйлерова цепь (задача о почтальоне).

8-я задача - Гамильтонова цепь.

9-я задача - метод ветвей и границ применительно к задаче о коммивояжере.

10-я задача - задача о назначениях; венгерский алгоритм.

11-я задача - тоже методом ветвей и границ.

G^ор(V,X)

Рис. 1

Задача1 Для неориентированного графа G, ассоциированного с графом G^ор выписать (перенумеровав вершины) :

а) множество вершин V и множество ребер X, G(V,X);

б) списки смежности;

в) матрицу инцидентности;

г) матрицу весов.

д) Для графа G^ор выписать матрицу смежности.

Нумерация вершин - см. Рис 1

а) V={0,1,2,3,4,5,6,7,8,9}

X={{0,1},{0,2},{0,3},{1,2},{1,4},{1,5},{1,6},{1,7},{2,3},{2,5},{3,8},{3,9},{4,5},{4,6},{5,3},{5,6},{5,8},{6,9},{7,8},{7,9},{8,9}}

В дальнейшем ребра будут обозначаться номерами в указанном порядке начиная с нуля.

б) Г0={1,2,3};

Г1={0,2,4,5,6,7};

Г2={0,1,3,5};

Г3={0,2,5,8,9};

Г4={1,5,6};

Г5={1,2,3,4,6,8};

Г6={1,4,5,9};

Г7={1,8,9};

Г8={1,3,5,7,9};

Г9={3,6,7,8};

в) Нумерация вершин и ребер соответственно п. а)

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
0	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	1	0	0	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0
2	0	1	0	1	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0
3	0	0	1	0	0	0	0	0	1	0	1	1	0	0	1	0	0	0	0	0	0
4	0	0	0	0	1	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0
5	0	0	0	0	0	1	0	0	0	1	0	0	1	0	1	1	1	0	0	0	0
6	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	1	0	1	0	0	0
7	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	1	1	0
8	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	1	0	1
9	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	1	1

г) Показана верхняя половина матрицы, т.к. матрица весов неориентированного графа симметрична относительно главной диагонали.

	0	1	2	3	4	5	6	7	8	9
0	¥	8	3	5	¥	¥	¥	¥	¥	¥
1		¥	1	¥	2	2	4	5	¥	¥
2			¥	2	¥	5	¥	¥	¥	¥
3				¥	¥	1	¥	¥	1	6
4					¥	4	2	¥	¥	¥
5						¥	2	¥	1	¥
6							¥	¥	¥	2
7								¥	1	1
8									¥	6
9										¥

д) Матрица смежности для графа G^ор.

	0	1	2	3	4	5	6	7	8	9
0	¥	1	1	1	¥	¥	¥	¥	¥	¥
1	-1	¥	1	¥	1	1	1	1	¥	¥
2	-1	-1	¥	1	¥	1	¥	¥	¥	¥
3	-1	¥	-1	¥	¥	-1	¥	¥	1	1
4	¥	-1	¥	¥	¥	1	1	¥	¥	¥
5	¥	-1	-1	1	-1	¥	1	¥	1	¥
6	¥	-1	¥	¥	-1	-1	¥	¥	¥	1
7	¥	-1	¥	¥	¥	¥	¥	¥	1	1
8	¥	¥	¥	-1	¥	-1	¥	-1	¥	1
9	¥	¥	¥	-1	¥	¥	-1	-1	-1	¥

Задача 2 Найти диаметр D(G), радиус R(G), количество центров Z(G) для графа G ; указать вершины, являющиеся центрами графа G.

D(G)=2

R(G)=2

Z(G)=10

Все вершины графа G(V,X) являются центрами.

Задача 3 Перенумеровать вершины графа G, используя алгоритмы:

а) "поиска в глубину";

б) "поиска в ширину".

Исходная вершина - a.

а)

б)

Задача 4 Используя алгоритм Прима найти остов минимального веса графа G. выписать код укладки на плоскости найденного дерева, приняв за корневую вершину a.

Вес найденного дерева - 14.

Код укладки дерева: 000011000001111111.

Задача 5 Используя алгоритм Дейкстра найти дерво кратчайших путей из вершины a графа G.

Вес найденного пути - 8.

Задача 6 Используя алгоритм Форда - Фалкерсона, найти максимальный поток во взвешенной двуполюсной ориентированной сети {G^ор , a , w}. Указать разрез минимального веса.

Последовательность насыщения сети (насыщенные ребра отмечены кружечками):

1-й шаг

2-й шаг

3-й шаг

4-й шаг

5-й шаг

6-й шаг

7-й шаг

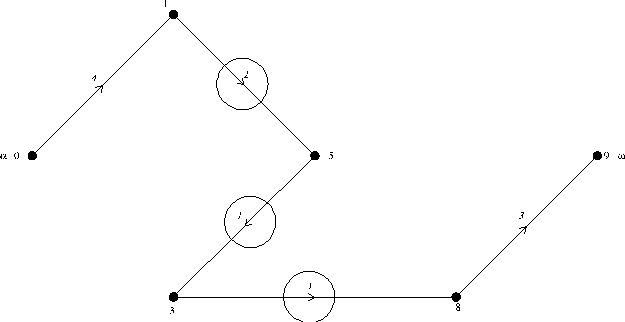
Окончательно имеем:

Как видно из рисунка, ребра {6,9},{7,9},{3,9}, питающие вершину w, насыщенны, а оставшееся ребро {8,9}, питающееся от вершины 8, не может получить большее значение весовой функции, так как насыщенны все ребра, питающие вершину 8. Другими словами - если отбросить все насыщенные ребра, то вершина w недостижима, что является признаком максимального потока в сети.

Максимальный поток в сети равен 12.

Минимальный разрез сети по числу ребер: {{0,1},{0,2},{0,3}}. Его пропускная способность равна 16

Минимальный разрез сети по пропускной способности: {{6,9}, {7,9}, {3,9}, {3,8}, {5,8}, {7,8}}. Его пропускная способность равна 12.

Задача 7 (Задача о почтальоне) Выписать степенную последовательность вершин графа G.

а) Указать в графе G Эйлерову цепь. Если таковой цепи не существует, то в графе G добавить наименьшее число ребер таким образом, чтобы в новом графе можно было указать Эйлерову цепь.

б) Указать в графе G Эйлеров цикл. Если такого цикла не существует, то в графе G добавить наименьшее число ребер таким образом, чтобы в новом графе можно было указать Эйлеров цикл.

Степенная последовательность вершин графа G:

(3,6,4,5,3,6,4,3,4,4)

а) Для существования Эйлеровой цепи допустимо только две вершины с нечетными степенями, поэтому необходимо добавить одно ребро, скажем между вершинами 4 и 7.

Полученная Эйлерова цепь: 0,3,2,0,1,2,5,1,4,5,6,1,7,4,6,9,7,8,9,3,8,5,3.

Схема Эйлеровой цепи (добавленное ребро показано пунктиром):

б) Аналогично пункту а) добавляем ребро {3,0}, замыкая Эйлерову цепь (при этом выполняя условие существования Эйлерова цикла - четность степеней всех вершин). Ребро {3,0} кратное, что не противоречит заданию, но при необходимости можно ввести ребра {0,7} и {4,3} вместо ранее введенных.

Полученный Эйлеров цикл: 0,3,2,0,1,2,5,1,4,5,6,1,7,4,6,9,7,8,9,3,8,5,3,0.

Схема Эйлерова цикла (добавленные ребра показаны пунктиром):

Задача 8

а) Указать в графе G^ор Гамильтонов путь. Если такой путь не существует, то в графе G^ор изменить ориентацию наименьшего числа ребер таким образом, чтобы в новом графе Гамильтонов путь можно было указать.

б) Указать в графе G^ор Гамильтонов цикл. Если такой цикл не существует, то в графе G^ор изменить ориентацию наименьшего числа ребер таким образом, чтобы в новом графе Гамильтонов цикл можно было указать.

а) Гамильтонов путь (ребра с измененной ориентацией показаны пунктиром):

б) Гамильтонов цикл (ребра с измененной ориентацией показаны пунктиром):

Задача 9 (Задача о коммивояжере) Дан полный ориентированный симметрический граф _> > с вершинами x_>1>, x_>2>,...x_>n>.Вес дуги x_>i>x_>j> задан элементами V_>ij> матрицы весов. Используя алгоритм метода ветвей и границ, найти Гамильтонов контур минимального (максимального) веса. Задачу на максимальное значение Гамильтонова контура свести к задаче на минимальное значение, рассмотрев матрицу с элементами _> >,где _> >. Выполнить рисунок.

Исходная таблица.

	x>1>	x>2>	x>3>	x>4>	x>5>	x>6>
x>1>	¥	3	7	2	¥	11
x>2>	8	¥	06	¥	4	3
x>3>	6	05	¥	7	¥	2
x>4>	6	¥	13	¥	5	¥
x>5>	3	3	3	4	¥	5
x>6>	8	6	¥	2	2	¥

Таблица Е _>>14

	x>1>	x>2>	x>3>	x>4>	x>5>	x>6>
x>1>	¥	1	5	01	¥	7	2
x>2>	8	¥	01	¥	4	1
x>3>	6	00	¥	7	¥	00
x>4>	1	¥	8	¥	01	¥	5
x>5>	01	00	00	1	¥	00	3
x>6>	6	4	¥	00	00	¥	2
						2

Дробим по переходу x_>2>-x_>3>:

Таблица _> >23 å=14+0=14

	x>1>	x>2>	x>4>	x>5>	x>6>
x>1>	¥	1	01	¥	7
x>3>	6	¥	7	¥	06
x>4>	1	¥	¥	01	¥
x>5>	01	01	1	¥	00
x>6>	6	4	00	00	¥

Таблица _> >23 å=14+1=15

	x>1>	x>2>	x>3>	x>4>	x>5>	x>6>
x>1>	¥	1	5	01	¥	7
x>2>	7	¥	¥	¥	3	03	1
x>3>	6	00	¥	7	¥	00
x>4>	1	¥	8	¥	01	¥
x>5>	01	00	05	1	¥	00
x>6>	6	4	¥	00	00	¥

Продолжаем по _> >23. Дробим по переходу x_>3>-x_>6>:

Таблица _> >23E36 å=14+0=14

	x>1>	x>2>	x>4>	x>5>
x>1>	¥	1	01	¥
x>4>	1	¥	¥	01
x>5>	01	01	1	¥
x>6>	6	¥	00	00

Таблица _> >23_>>36 å=14+6=20

	x>1>	x>2>	x>4>	x>5>	x>6>
x>1>	¥	1	01	¥	7
x>3>	01	¥	1	¥	¥	6
x>4>	1	¥	¥	01	¥
x>5>	00	01	1	¥	07
x>6>	6	4	00	00	¥

Продолжаем по _> >23_>>36. Дробим по переходу x_>4>-x_>5>:

Таблица _> >23E36_>>45 å=14+0=14

	x>1>	x>2>	x>4>
x>1>	¥	1	01
x>5>	01	01	1
x>6>	6	¥	00

Таблица _> >23_>>36_>>45 å=14+1=15

	x>1>	x>2>	x>4>	x>5>
x>1>	¥	1	01	¥
x>4>	00	¥	¥	¥	1
x>5>	01	01	1	¥
x>6>	6	¥	00	00

Продолжаем по _> >23_>>36_>>45. Дробим по переходу x_>5>-x_>1>:

Таблица _> >23_>>36_>>45_>>51 å=14+1=15

	x>2>	x>4>
x>1>	1	¥	1
x>6>	¥	00

Таблица _> >23_>>36_>>45_>>51 å=14+6=20

	x>1>	x>2>	x>4>
x>1>	¥	1	01
x>5>	¥	01	¥
x>6>	0	¥	00
	6

Окончательно имеем Гамильтонов контур: 2,3,6,4,5,1,2.

Прадерево разбиений:

Задача 10 (Задача о назначениях) Дан полный двудольный граф K_>nn> с вершинами первой доли x_>1>, x_>2>,...x_>n>.и вершинами другой доли y_>1>, y_>2>,...y_>n>..Вес ребра {xi_>,>y_>j>} задается элементами v_>ij> матрицы весов. Используя венгерский алгоритм, найти совершенное паросочетание минимального (максимального веса). Выполнить рисунок.

Матрица весов двудольного графа K_>55 > :

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	2	0	0	0	0
x>2>	0	7	9	8	6
x>3>	0	1	3	2	2
x>4>	0	8	7	6	4
x>5>	0	7	6	8	3

Первый этап - получение нулей не нужен, т. к. нули уже есть во всех строк и столбцах.

Второй этап - нахождение полного паросочетания.

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	2	0	0	0	0
x>2>	0	7	9	8	6
x>3>	0	1	3	2	2
x>4>	0	8	7	6	4
x>5>	0	7	6	8	3

Третий этап - нахождение максимального паросочетания.

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	2	0	0	0	0	X
x>2>	0	7	9	8	6	X
x>3>	0	1	3	2	2
x>4>	0	8	7	6	4
x>5>	0	7	6	8	3
	X	X

Четвертый этап - нахождение минимальной опоры.

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	2	0	0	0	0
x>2>	0	7	9	8	6	5
x>3>	0	1	3	2	2	1
x>4>	0	8	7	6	4	2
x>5>	0	7	6	8	3	3
	4

Пятый этап - возможная перестановка некоторых нулей.

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	3	0	0	0	0
x>2>	0	6	8	7	5	5
x>3>	0	0	2	1	1	1
x>4>	0	7	6	5	3	2
x>5>	0	6	5	7	2	3
	4

Решение с ненулевым значением. Переход ко второму этапу.

Полное паросочетание:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	3	0	0	0	0
x>2>	0	6	8	7	5
x>3>	0	0	2	1	1
x>4>	0	7	6	5	3
x>5>	0	6	5	7	2

Максимальное паросочетание:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	3	0	0	0	0	X
x>2>	0	6	8	7	5	X
x>3>	0	0	2	1	1
x>4>	0	7	6	5	3
x>5>	0	6	5	7	2
	X	X

Минимальная опора:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	3	0	0	0	0	6
x>2>	0	6	8	7	5	7
x>3>	0	0	2	1	1	1
x>4>	0	7	6	5	3	2
x>5>	0	6	5	7	2	3
	4	5

Перестановка нулей:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	3	0	0	0	0	6
x>2>	0	6	8	7	5	7
x>3>	0	0	2	1	1	1
x>4>	0	7	6	5	3	2
x>5>	0	6	5	7	2	3
	4	5

Полное паросочетание:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	3	0	0	0	0	6
x>2>	0	6	8	7	5	7
x>3>	0	0	2	1	1	1
x>4>	0	7	6	5	3	2
x>5>	0	6	5	7	2	3
	4	5

Максимальное паросочетание:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	3	0	0	0	0	X
x>2>	0	6	8	7	5
x>3>	0	0	2	1	1	X
x>4>	0	7	6	5	3	X
x>5>	0	6	5	7	2
	X	X	X

Минимальная опора:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	3	0	0	0	0
x>2>	0	6	8	7	5	1
x>3>	0	0	2	1	1
x>4>	0	7	6	5	3
x>5>	0	6	5	7	2	2
	3

Перестановка нулей:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	5	0	0	0	0
x>2>	0	4	6	5	3	1
x>3>	2	0	2	1	1
x>4>	2	7	6	5	3
x>5>	0	4	3	5	0	2
	3

Полное паросочетание:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	5	0	0	0	0
x>2>	0	4	6	5	3
x>3>	2	0	2	1	1
x>4>	2	7	6	5	3
x>5>	0	4	3	5	0

Максимальное паросочетание:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	5	0	0	0	0	X
x>2>	0	4	6	5	3	X
x>3>	2	0	2	1	1	X
x>4>	2	7	6	5	3
x>5>	0	4	3	5	0	X
	X	X	X		X

Минимальная опора:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	5	0	0	0	0
x>2>	0	4	6	5	3
x>3>	2	0	2	1	1
x>4>	2	7	6	5	3	1
x>5>	0	4	3	5	0

Перестановка нулей:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	5	0	0	0	0
x>2>	0	4	6	5	3
x>3>	2	0	2	1	1
x>4>	0	5	4	3	1	1
x>5>	0	4	3	5	0

Полное паросочетание:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	5	0	0	0	0
x>2>	0	4	6	5	3
x>3>	2	0	2	1	1
x>4>	0	5	4	3	1	1
x>5>	0	4	3	5	0

Максимальное паросочетание:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	5	0	0	0	0	X
x>2>	0	4	6	5	3	X
x>3>	2	0	2	1	1	X
x>4>	0	5	4	3	1
x>5>	0	4	3	5	0	X
	X	X	X		X

Минимальная опора:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	5	0	0	0	0
x>2>	0	4	6	5	3	3
x>3>	2	0	2	1	1
x>4>	0	5	4	3	1	1
x>5>	0	4	3	5	0
	2

Перестановка нулей:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	6	0	0	0	0
x>2>	0	3	5	4	2	3
x>3>	3	0	2	1	1
x>4>	0	4	3	2	0	1
x>5>	1	4	3	5	0
	2

Полное паросочетание:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	6	0	0	0	0
x>2>	0	3	5	4	2	3
x>3>	3	0	2	1	1
x>4>	0	4	3	2	0	1
x>5>	1	4	3	5	0
	2

Максимальное паросочетание:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	6	0	0	0	0	X
x>2>	0	3	5	4	2	X
x>3>	3	0	2	1	1	X
x>4>	0	4	3	2	0
x>5>	1	4	3	5	0	X
	X	X	X		X

Минимальная опора:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	6	0	0	0	0
x>2>	0	3	5	4	2	4
x>3>	3	0	2	1	1
x>4>	0	4	3	2	0	1
x>5>	1	4	3	5	0	5
	2				3

В результате имеем:

	y>1>	y>2>	y>3>	y>4>	y>5>
x>1>	6	0	0	0	0
x>2>	0	1	3	2	2	4
x>3>	3	0	2	1	1
x>4>	0	2	1	0	0	1
x>5>	1	4	3	5	0	5
	2				3

Исходный граф

Полученный граф:

Вес найденного совершенного паросочетания = 12.

Задача 11 Решить задачу 10, используя алгоритм ветвей и границ (отождествив вершины x_>i> и y_>j>).

Таблица Е (исходная). Строки - x_>i> , столбцы - y_>j>. å=0

	1	2	3	4	5
1	2	01	03	02	02
2	06	7	9	8	6
3	01	1	3	2	2
4	04	8	7	6	4
5	03	7	6	8	3

Дробим по переходу x_>2> - y_>1>:

Таблица Е21 å=0+8=8

	2	3	4	5
1	00	02	01	00
3	01	2	1	1	1
4	4	3	2	02	4
5	4	3	5	03	3

Таблица _> >21 å=0+6=6

	1	2	3	4	5
1	2	01	03	02	00
2	¥	1	3	2	01	6
3	01	1	3	2	2
4	04	8	7	6	4
5	03	7	6	8	3

Продолжаем по _> >21:

Дробим по переходу x_>4> - y_>1>:

Таблица _> >21Е41 å=6+4=10

	2	3	4	5
1	00	02	01	00
2	1	3	2	01
3	01	2	1	1	1
5	4	3	5	03	3

Таблица _> >21_>>41 å=6+4=10

	1	2	3	4	5
1	2	01	03	02	00
2	¥	1	3	2	01
3	01	1	3	2	2
4	¥	4	3	2	02	4
5	03	7	6	8	3

Продолжаем по Е21:

Дробим по переходу x_>5> - y_>5>:

Таблица Е21Е55 å=8+2=10

	2	3	4
1	00	01	00
3	01	2	1
4	2	1	01	2

Таблица Е21_>>55 å=8+3=11

	2	3	4	5
1	00	02	01	00
3	01	2	1	1
4	4	3	2	02
5	1	01	2	¥	3

Продолжаем по Е21Е55:

Дробим по переходу x_>3> - y_>2>:

Таблица Е21Е55Е32 å=10+0=10

	3	4
1	01	00
4	1	01

Далее решение очевидно: x_>1> - y_>3> и x_>4> - y_>4>. Это не увеличит оценку.

В итоге имеем совершенное паросочетание с минимальным весом:

Прадерево разбиений:

Литература

1. Грешилов А.А. Как принять наилучшее решение в реальных условиях:-М.:Радио и связь, 1991.-320с.:ил.

2. Беллман Р. Динамическое программирование: Пер. с англ./Под ред. Н.Н. Воробьева.-М.: ИЛ, 1960.-400 с.

3. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования: Пер с англ./Под ред. А.А. Первозванского.-М.: Наука, 1965.-458 с.

4. Вентцель Е.С. Исследование операций.-М.: Сов. радио, 1972.-551 с.

5. Вильямс Н.Н. Параметрическое программирование в экономике (методы оптимальных решений):-М.:Статистика, 1976.-96с.

6. Гольштейн Е.Г., Юдин Д.Б. Новые направления в линейном программировании:-М.: Сов радио, 1966.- 524 с.

7. Зангвилл У.И. Нелинейное программирование: Пер. с англ./Под ред. Е.Г. Гольштейна.-М.: Сов радио, 1973.- 312 с.

8. Зуховицкий С.И., Авдеева Л.И. Линейное и выпуклое программирование (справочное руководство).-М.: Наука, 1964.-348 с.

9. Исследование операций. Методологические основы и математические методы: Пер. с англ./ Под ред. И.М. Макарова, И.М. Бескровного.-М.: Мир, 1981.- Т.1.-712 с.

10. Исследование операций. Модели и применение: Пер. с англ./ Под ред. И.М. Макарова, И.М. Бескровного.-М.: Мир, 1981.- Т.1.-712 с.

11. Лазарев В.Г., Лазарев Ю.В. Динамическое управление потоками информации в сетях связи.-М.: Радио и связь, 1983.- 216 с.

12. Мартин Дж. Системный анализ передачи данных.: Пер с англ./ Под ред. В.С. Лапина.-М.: Мир, 1975.- М.2.- 431 с.

13. Монаков В.М., Беляева Э.С., Краснер Н.Я. Методы оптимизации. Пособие для учителя.-М.: Просвещение, 1978.- 175с.

14. Муртаф Б. Современное линейное программирование: Теория и практика. Пер. с англ./Под ред. И.А. Станевичуса.- М.: Мир, 1984.- 224 с.

15. Рокафеллор Р. Выпуклый анализ: Пер. с англ./Под ред. А.Д. Иоффе, В.М. Тихомирова.-М.: Мир, 1973.- 469 с.

16. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации.- М.:- Наука, Физматгиз, 1986.- 326 с.

17. Ху Т. Целочисленное программирование и потоки в сетях: Пер. с англ./Под ред. А.А. Фридмана.- М.: Мир, 1974.-419 с.

18. Фиакко А., Мак-Кормик Г. Нелинейное программирование. Методы последовательной безусловной минимизации: Пер. с англ./Под ред. Е.Г. Гольштейна. -М.:- Мир, 1972.- 240 с.

19. Филлипс Д., Гарсиа-Диас А. Методы анализа сетей: Пер. с англ./ Под ред. Б.Г. Сушкова.- М.: Мир, 1984.- 496 с.

20. Юдин Д.Б., Гольштейн Е.Г. Линейное программирование. Теория и конечные методы,- М.:- Физматгиз, 1963.- 775 с.