Об одной общей краевой задаче со смещением для нагруженного уравнения третьего порядка с кратными характеристиками

Кодзодков А.Х.

Кафедра математического анализа.

Кабардино-Балкарский государственный университет

Рассмотрим линейное нагруженное уравнение третьего порядка:

(1)

в – области , ограниченной отрезками прямых соответственно при и характеристиками , уравнения (1) при ; ; – интервал , – интервал .

Здесь положено, что:

или 2) .

Пусть имеет место случай (1).

Задача . Найти функцию со следующими свойствами: 1) ;

2) – регулярное решение уравнения (1) при ;

3) удовлетворяет краевым условиям

, ; (2)

, (3)

где , – аффиксы точек пересечения характеристик уравнения (1) при y < 0, выходящих из точки с характеристиками АС и ВС соответственно; , , .

Опираясь на однозначную разрешимость задачи Коши для уравнения (1) при y < 0 с начальными данными , , легко видеть, что если существует решение задачи , то оно представимо в виде:

. (4)

Учитывая (4) в краевом условии (3), получаем:

, (5)

где .

Следуя [1], обозначим через первообразную функции . Тогда уравнение (5) примет вид:

, (6)

, (7)

где .

Относительно коэффициентов уравнения (6) будем рассматривать аналогичные ситуации, приведенные в работе [1]:

1) , т.е. ;

2) , , т.е. ;

3), т.е. ;

4) , , т.е. .

Пусть имеет место случай (1) и функции . Решение задачи (6), (7) в этом случае имеет вид:

, (8)

где .

Дифференцируя равенство (8) и делая несложные преобразования, получаем:

(9)

где ,

, ,

, .

Переходя к пределу в уравнении (1) при , получаем функциональное соотношение между и , принесенное из области , на линию :

. (10)

В силу граничных условий (2) и равенства (9) получим нелокальную задачу для нагруженного неоднородного интегро-дифференциального уравнения третьего порядка с переменными коэффициентами:

, (11)

, (12)

где

В начале положим, что , т.е.

, , т.е.

В зависимости от значений корней характеристического уравнения

, (13)

соответствующего однородному уравнению (11) (), будем исследовать разрешимость задачи (11), (12).

Введем обозначение . Логически возможны три различных случая: 1) S>0, 2) S=0, 3) S<0.

Известно, что [2]: 1) если S>0, то уравнение (13) имеет только один действительный корень, а два остальных корня будут сопряженными чисто комплексными числами; 2) если S=0, то все три корня уравнения (13) действительны, причем два из них равны; 3) если S<0, то все три корня уравнения (13) действительны, причем все они различны.

Пусть S=0, т.е. .

Общее решение уравнения (11) в этом случае имеет вид:

, (14)

где ,

Удовлетворяя (14) граничным условиям (12), получим линейную алгебраическую систему трех уравнений относительно с определителем:

Положим, что . Тогда находят по формулам:

, (15)

, (16)

, (17)

где

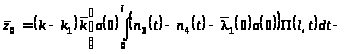
Учитывая (15) – (17) в (14), получаем:

где ,

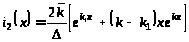или

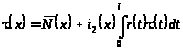, (18)

где .

Если считать функцию известной, то (18) представляет собой интегральное уравнение Фредгольма второго рода с вырожденным ядром относительно . Обозначив

решение уравнения (18) будем искать в виде:

. (19)

После подстановки (19) в (18) имеем выражение:

Если , то определяется по формуле:

. (20)

Учитывая (19), (20) в (18), получаем:

, (21)

где ,

В равенстве (21) учтем значение . В результате будем иметь:

, (22)

где ,

Перепишем уравнение (22) в виде:

, (23)

где .

В силу условий, наложенных на заданные функции , можем заключить, что , следовательно .

Обращая интегральное уравнение Вольтерра второго рода (23), получаем:

, (24)

где – резольвента ядра . Заметим, что резольвента обладает такими же свойствами, что и ядро [3].

Заменяя в равенстве (24) функцию ее значением, получаем:

, (25)

где ,

Перепишем уравнение (25) в виде:

, (26)

где .

Решение уравнения (26) будем искать в виде:

, (27)

где .

Поступая аналогично предыдущему случаю, получим

, если .

Таким образом, имеем:

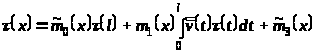, (28)

где .

Уравнение (28) перепишем в виде:

, (29)

где .

Решение уравнения (29) ищем в виде:

, (30)

где .

Подберем теперь постоянную так, чтобы определенная формулой (30) функция была решением интегрального уравнения (29). С этой целью внесем выражение (30) для в левую часть (29). После простых вычислений получаем:

откуда

где положено, что

Таким образом, имеем:

. (31)

Полагая в равенстве , находим

если , т.е.

Пусть теперь имеет место случай 2), причем :

В этом случае уравнение (6) принимает вид:

, (32)

где .

Учитывая условие (7), из (32) получаем соотношение , . Подставляя это значение в (32), находим

. (33)

Подставляя (33) в (10), получаем нагруженное уравнение:

, (34)

где ,

с внутренне-краевыми условиями (12).

Рассмотрим частный случай, когда , т.е.

=; , т.е.

; , т.е.

Тогда общее решение однородного уравнения

имеет вид [4]:

где .

Пусть . Методом вариации постоянных находим общее решение неоднородного уравнения (34) в виде:

, (35)

где ,

Удовлетворяя (35) условиям (12), получаем:

где

, причем выполняется условие

, т.е. .

Равенство (35) перепишем в виде:

, (36)

где , .

Из (36) при , имеем

если выполняется условие , т.е.

Пусть имеет место случай 3), причем , . Тогда уравнение (6) принимает вид [1]:

. (37)

Полагая в равенстве (37) и, учитывая условия , получим:

Следовательно, для имеем представление

, (38)

где .

Если выполняется условие 4) и функции , причем , то имеем равенство

. (39)

Полагая в равенстве (39) и, учитывая условие , находим

Таким образом, имеем, что

. (40)

Полагая в равенствах (38), (40) , найдем , а затем, подставляя их в равенство (10), однозначно найдем неизвестную функцию .

Случай исследуется аналогично.

После определения функций решение задачи в области задается формулой (4), а в области приходим к задаче (1), (2), .

Решение этой задачи дается формулой [5]:

, (41)

где

Отсюда, полагая в равенстве (41) , получаем систему интегральных уравнений типа Вольтерра второго рода:

(42)

где ,

В силу свойств функции и ядер системы (42), нетрудно убедиться, что система уравнений (42) допускает единственное решение в пространстве [3].

Список литературы

Наджафов Х.М. Об одной общей краевой задаче со смещением для уравнения Лаврентьева-Бицадзе // Известия КБНЦ РАН. Нальчик, №1(8), 2002.

Фадеев Д.К. Лекции по алгебре. М.1984.

Мюнтц Г. Интегральные уравнения. Л.-М., Т.1, 1934.

Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1971.

Джураев Т.Б. Краевые задачи для уравнений смешанного и смешанно-составного типов. Ташкент: Фан, 1979.

Для подготовки данной применялись материалы сети Интернет из общего доступа