Тригонометрия (работа 3)

Действительные числа:

Теорема: R - несчётное множество.

Док-во: метод от противного. Несчётность (0;1)

X_>1>=0,n_>11>n_>12>n_>13>…n_>1k>… m_>1>Î{0,1,…,9}\{9,n_>11>}

X_>2>=0,n_>21>n_>22>n_>23>…n_>2k>… m_>2>Î{0,1,…,9}\{9,n_>22>}

……………………… ………………………

X_>k>=0,n_>k1>n_>k2>n_>k3>…n_>kk>… m_>k>Î{0,1,…,9}\{9,n_>kk>}

a=0,m_>1>m_>2>…m_>k>… Þ a¹x_>1> a¹x_>2> a¹x_>3> …… a¹x_>k>

aÏ(0;1) Противоречие.

0<a<1 Þ R - несчётное множество.

Теорема: Q - Счётное множество.

Док-ть: Q⁺ - счётное, т.к. Q=Q^-U{0}UQ⁺

Док-во:

_> >

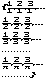Q⁺ - счётное множество, т.к. оно есть объединение счётного семейства счётных

множеств. Q^- - Тоже, что и Q⁺ только все элементы множества отрецательные

. По теореме: Всякое множество счётных одмножеств явл. Само счётным Þ Q - сч. мн.

Предел числовой последовательности:

Пусть aÎR, e>0 {x:| x-a|<e}

Последовательность {X_>n>} имеет конечный предел если сущ. такое число a?R, что кокого

бы нибыло e>0 почти все члены этой последовательности e - окрестность точки a.

Почти все - это значит за исключением быть может конечного числа.

$n_>0>=n_>0>(e)ÎN: n>n_>0> Þ |x_>n>-a|<e a=limx_>n> , при n®¥

Свойства:

1. Единственность (Если предел есть, то только один)

Док-во: Метод от противного. a=limx_>n >, b=limx_>n >, при n®¥, a>b, a-b=e>0

$n_>0>=n_>0>(e/3):|x_>n>-a|<e/3 и |x_>n>-b|<e/3

e=a-b=(a-x_>n>)-(b-x_>n>)

e=|(a-x_>n>)-(b-x_>n>)|£ |(a-x_>n>)|+|(b-x_>n>)|£2e/3

e£2e/3 Противоречие.

2. Ограниченность (Если последовательность имеет конечный предел, то она ограничена)

Дано: $limx_>n>=a, при n®¥ - конечный предел

Док-ть:$M>0:|x_>n>|<M "n

Док-во: limx_>n>=a, при n®¥:"e>0 $n_>0>=n_>0>(e):a-e<x_>n><a+e, при n>n_>0>

Пусть e=1, тогда при n>n_>0>(1) будет выполняться a-1<x_>n><a+1 или |x_>n>-a|<1

Тогда |x_>n>|<|(x_>n>-a)+a|<|x_>n>-a|+|a|<|a|+1 "n>n_>0>(1)

P=max{|a_>1>|,|a_>2>|,…,|a_>no>|}

M=max{P,|a|+1}Þ|x_>n>|<M "n

3. Предел подпоследовательности (Если последовательность имеет предел а, то любая

её подпоследовательность имеет тоже предел а)

Свойства предельного перехода связанные с неравенствами:

Теорема 1. Пусть $limx_>n>=x, при n®¥ - конечный (1 последовательность)

$limy_>n>=y, при n®¥ - конечный (2 последовательность)

Если x<y, то для почти всех n x_>n><y_>n>

Док-во: e=y-x>0

$n^|=n^|(e/3): |x_>n>-x|<e/3 "n>n^|

$n^||=n^||(e/3): |y_>n>-y|<e/3 "n>n^|

n_>0>=max{n^|,n^||}, n>n_>0>

x-e/3<x_>n><x+e/3 î

y-e/3<y_>n><y+e/3 ì Þ x_>n><x+e/3<y-e/3<y_>n> Þ "n>n_>0> x_>n><y_>n> Что и т. док-ть.

Следствие: Если последовательность имеет предел отличный от нуля, то

эта последовательность отделена от нуля. Эта последовательность при больших n

сохраняет знак своего предела)

x=limx_>n>, x¹0

1) x>0 Предположим x>0 x/2>0Þx>x/2

limx_>n>>x/2, при n®¥ Из Т.1. следует, что $n_>0>:"n>n_>0> x_>n>>x/2>0

Теорема 2. Предположим, что $limx_>n>=x и $limy_>n>=y, при n®¥

Если для почти всех n:x_>n>£y_>n>, то и x£y

Док-во: Метод от противного. x>y по Т.1. Þ x_>n>>y_>n> для почти всех n

Противоречие.

Теорема 3. Теорема о двустороннем ограничении.

Пусь $limx_>n>=limy_>n>=a, при n®¥, и предположим, что x_>n>£z_>n>£y_>n> "n, тогда

1) Сущ. limz_>n>, при n®¥

2) limz_>n>=a, при n®¥

Док-во: $n^|=n^|(e):a-e£x_>n>£a+e, "n>n^|

$n^||=n^||(e):a-e£y_>n>£a+e, "n>n^||

n_>0>=max{n^|,n^||}

n>n_>0> Þ a-e£x_>n>£z_>n>£y_>n>£a+e Þ a-e£z_>n>£a+e Þ $limz_>n>=a

Бесконечно малые и бесконечно большие последовательности:

defû {x_>n>}-б.м. :=limx_>n>=0, при n®¥, т.е. "e>0 $n_>0>=n_>0>(e) n>n_>0> Þ |x_>n>|<e

defû {x_>n>}-б.б. :=limx_>n>=¥, при n®¥, т.е. "e>0 $n_>0>=n_>0>(e) n>n_>0> Þ |x_>n>|>e

Свойство 1. Произведение б.м. последов. на ограниченную даёт сного б.м.

{x_>n>}-б.м. {y_>n>}-ограниченная {x_>n>y_>n>}-б.м.

Док-во: $M>0:|y_>n>|£M "n - значит ограничена.

"e>0 $n_>0>=n_>0>(e/M):n>n_>0> Þ |x_>n>|<e/M Þ

Þ n>n_>0> |x_>n>y_>n>|=|x_>n>||y_>n>|£e/M*M=e Þ {x_>n>y_>n>}-б.м.

Свойство 2. Произведение б.б. на посл. Отделённую от нуля даст б.б.

{x_>n>}-б.б. и {y_>n>}-отдел от нуля

Док-во: {1/x_>n>*1/y_>n>}=б.м.*огран.=б.м. (по 1-ому свойству)Þ {x_>n>y_>n>}-б.б.

Свойство 3. Сумма двух (любого кон. числа) б.м. послед. Даст снова б.м.

{x_>n>} и {y_>n>}-б.м. Þ{x_>n>+y_>n>}-б.м.

Док-во: "e $n^|=n^|(e/2):n>n^| |x_>n>|<e/2

$n^||=n^||(e/2):n>n^|| |y_>n>|<e/2

n_>0>=max{n^|,n^||}

n>n_>0> Þ |x_>n>+y_>n>|£|x_>n>|+|y_>n>|<e/2+e/2=e

Для того чтобы получить это св-во с любым числом последовательностей

нужно применить метод мат. индукции.

Свойство 4. Сумма б.б. одного знака снова б.б. того же знака

Док-во: Очивиднл.

Неопределённые интегралы.

def / F(x) называется первообразной

для f(x) на [a;b] если F ¢(x)=f(x)

У непрерывной функции первообразная

всегда есть.

Теорема: Различные первообразные

одной и той же функции отличаются

на одно и тоже постоянное слагаемое.

Док-во: F_>1>(x) и F_>2>(x) – первообразные для f(x)

F(x)= F_>1>(x)- F_>2>(x)

F ¢(x)= F_>1>¢(x)- F_>1>¢(x)=f(x)-f(x)=0

F(x)=const

Def / Совокупность всех первообразных одной

и той же функции называется её

неопределённым интегралом.

_>>

_>>

_>>

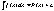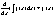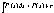Св-ва линейности:

_> >

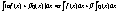Замена переменных в неопределённом интеграле

или методом подстановки.

Теорема: Пусть функция x=

x(t): (a;b)®(a;b), xÎC¹(a;b), fÎC(a;b)

1) _> >

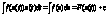½x=x(t)

2) Если x¢(t) сохраняет знак, тогда

_>>

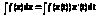½t=t(x)

Док-во: 1) d/dxF(x(t))=F ¢(x(t))x¢(t)=f(x(t))x¢(t)

2) x(t) – строго монотонная Þ $обратная t=t(x)

_>>

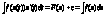½t=t(x)

Интегрирование по частям.

_>>

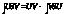Рекуррентная формула.

_>>

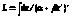y=a+bx² y¢=2bx xy¢=2bx²=2(y-a)

U=1/yⁿ dx=dV dU=(-ny¢/yⁿ⁺¹)dx V=x

_>>

_>>

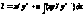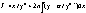I_>n>=x/yⁿ+2nI_>n>-2naI_>n+1>

1) I_>n+1>=(1/2na)(x/yⁿ+(2n-1)I_>n>), n¹0, a¹0

2) I_>n>=(1/(2n-1))(2naI_>n+1>-x/yⁿ), n¹1/2, a¹0

Поле комплексных чисел.

(x;y)=(x;0)+(y;0)(0;1)=x+yi

– алгебраическая запись комплексного числа

Чертёж :