Теория математической статистики
Теория математической статистики
Введение
Истоками математической статистики (М.С.) является большой объем статистических данных и потребность после их специальной обработки сделать прогноз развития исходной ситуации.
Первый раздел М.С. – описательная статистика – предназначена для сбора, представления в удобном виде и описания исходных данных. Описательная статистика обрабатывает два вида данных: количественные и качественные.
К количественным относятся рост, вес и т.д. к качественным – тип темперамента, пол.
Описательная статистика позволяет описать, обобщить, свести к желаемому виду свойства массивов данных.
Второй раздел М.С. – теория статистического вывода – это формализованная система методов решения задач, сводящихся к попытке вывести свойства большого массива данных путем обследования его малой части.
Статистический вывод строится на описательной статистике и от частных свойств выборки данных мы переходим к частным свойствам совокупности.
Третий раздел М.С. - планирование и анализ эксперта. Разработана для обнаружения и анализа причинных связей между переменными.
Измерение, шкалы и статистика
Измерение – это приписывание чисел объектам в соответствии с определенными правилами. Числа – это удобные в обработке объекты, в которые мы преобразуем определенные свойства нашего восприятия.
Шкала наименований или номинальная шкала. Номинальное измерение сводится к разбиению совокупности объектов на классы в каждом из которых сосредоточены объекты, идентичные по какому-нибудь признаку или свойству, например, по национальности, по полу, по типу темперамента.
При данных измерениях каждому из классов присваивается число, но оно используется исключительно как название этого класса и никаких операций над этими числами производить не предполагается.
Порядковое измерение возможно только тогда, когда в квалифицируемых объектах можно различить разную степень признака и свойства, на основе которого производится квалификация (например, конкурс красоты “Умники и умницы”). В данном случае числа используют только одно свое свойство – способность упорядочиваться.
Интервальная шкала принимается тогда, когда можно определить не только количество, свойства или признака в объекте, но также зафиксировать равные различия между объектами, то есть можно ввести единицу измерения для свойства или признака (например, температура, возраст).
Числа при интервальных измерениях имеют свойство упорядоченности и однозначности. Равные разности чисел соответствуют равным разностям значений измеряемого свойства или признака объекта.
Шкала отношений отличается от интервальной только тем, что точка отсчета не произвольна, а указывает на полное отсутствие измеряемого свойства или признака объекта.
Переменные и их измерение
Переменные бывают дискретные и непрерывные. При измерениях, особенно непрерывных свойств или признаков, можно достигнуть только косвенного значения переменной, то есть приближенного к точному и степень этого приближения будет определяться чувствительностью измерения.
Чувствительность определяется минимальной единицей цифровой шкалы, имеющейся в нашем распоряжении.
Пределы для точного значения устанавливаются путем прибавления и вычитания половины чувствительности измерительного процесса.
Множество чисел записывается с использованием произвольной величины с индексом, который указывает порядковый номер величины в цепи данных (x>i>).
Обозначение S и его свойства
1. >
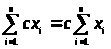 >
>
2. >
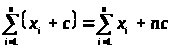 >
>
3. >
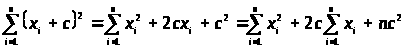 >
>
4. >
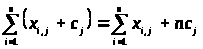 >
>
5. >
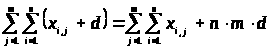 >
>
Табулирование и представление данных
Перед анализом и интерпретацией данных их обобщают.
Обобщение – запись данных в виде таблицы. Самый элементарный этап.
Ранжирование – упорядочение переменных от максимального до минимального или наоборот. Такое упорядочивание называется несгруппированным рангом.
Распределение частот. Проранжированный список сворачивают, указывая все полученные измерения подряд, однократно, а в соседней графе указывают частоту, с которой встречается данная оценка
Распределение сгруппированных частот применяется при большом количестве оценок (100 и более). Оценки группируются по признакам и каждая такая группа называется разрядом оценок. В случае полного поглощения этими группами всех данных, мы говорим о распределении сгруппированных частот.
Построение распределения сгруппированных частот
|
Оценки |
Интервал |
Подсчет |
Частота |
|
90 95 51 112 |
110-114 |
1 |
1 |
|
66 78 109 62 |
105-109 |
111 |
3 |
|
106 70 89 91 |
100-104 |
11 |
2 |
|
84 47 58 93 |
95-99 |
1111 |
4 |
|
105 95 59 84 |
90-94 |
111 |
3 |
|
83 100 72 |
85-89 |
1 |
1 |
|
104 69 74 |
80-89 |
111111 |
6 |
|
82 44 75 |
75-79 |
1111 |
4 |
|
97 80 81 |
70-74 |
1111 |
4 |
|
97 75 71 |
65-69 |
111 |
3 |
|
59 75 68 |
60-64 |
1 |
1 |
|
55-59 |
111 |
3 |
|
|
50-54 |
1 |
1 |
|
|
45-49 |
1 |
1 |
|
|
44-45 |
1 |
1 |
Предварительно образовывать не менее 12 и более 15. Меньше 12 искажает результат, более 15 затрудняет работу с таблицей.
1) Определяем размах – разницу между максимальной и минимальной оценкой (112-44=69)
2) Выбор интервала разряда: 69:12=5,75
Определяем с уменьшением до 5: 69:15=4,6
3) Определение границ раздела. Необходимо образовать достаточное количество разрядов, чтобы не потерять самую маленькую и самую большую оценки, поэтому табулирование начнем с величины кратной интервалу. Ближайшее кратное 5 ниже нижней оценки – это 40. И делим на разряды до тех пор, пока не будет охвачена самая высокая оценка. Если необходимо сравнить 2 и более выборки, их помещают в такую же таблицу.
Квантили
Квантили – это способ описать группу измерений. Квантиль – это общее понятие.
Квантиль – точка на числовой шкале, которая делит совокупность наблюдений на группы с соответствующими пропорциями в каждой из них.
Квартиль – делит наблюдения на 4 группы (Q)
Дециль – делит наблюдения на 10 групп (D)
Квинтель – делит наблюдения на 5 групп (К)
Процентиль – делит наблюдения на 100 групп (Р)
Определение процентелей
Процентель представляет собой точку, ниже которой лежит Р % - в оценок.
Вычисление процентеля
|
Оценка |
38 |
37 |
36 |
35 |
34 |
33 |
32 |
31 |
30 |
28 |
29 |
27 |
26 |
25 |
24 |
|
Частота |
1 |
1 |
3 |
5 |
9 |
8 |
17 |
23 |
24 |
18 |
10 |
3 |
1 |
0 |
2 |
|
Накопленная частота |
125 |
124 |
123 |
120 |
115 |
106 |
98 |
81 |
58 |
16 |
34 |
6 |
3 |
2 |
Для определения 25 процентиля P>25> (границы под которой расположены 25% всех выставленных оценок)
Общая формула:
>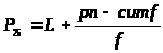 >
>
где:
n – общее число оценок
L – фактическая нижняя граница того раздела оценок, который включает себя нужную нам оценку
cumf – накопленная в данной нижней границе частота
f – количество оценок в данном разделе
p – определяемый процентиль (в данном случае 0,25)
p*n = 0,25*125=31,25
Находим фактическую нижнюю границу раздела L, содержащую 31,5 (это между 34 и 16).
Нижняя граница оценки 28,5
L=28,5 f=34-16=18
Вычитаем накопленную частоту L из произведения nf: ((31,25-16)/18) + 28,5=29,35
Для определения процентиля в случае наличия интервалов оценок, формула принимает вид:
>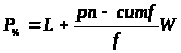 >
>
где W – ширина любого интервала оценок (в примере =1).
Наглядное представление данных
В табличных процессорах представляется возможность оформить численные данные в виде графика или диаграммы различного вида, но разновидностей графического представления данных существует больше, чем это предусмотрено программным обеспечением и прежде чем использовать какой-либо из видов необходимо:
выделить в данных существенную информацию;
знать все типы представления данных и сделать правильный выбор;
знать и грамотно использовать потенциал аудитории, для представления которой готовятся данные;
если оформление осуществляется не вами, разработать подробные и четкие инструкции для технического персонала с учетом имеющихся средств.
Примеры диаграмм и графиков: линейная, столбиковая, полосчатая, кумулятивная кривая, данные накапливаются с течением времени, пиктограмма – данные представляются в виде стилизованных изображений (улов рыбы в виде рыбы), логарифмическая диаграмма, круговая диаграмма.
Графическое представление распределения частот
Столбиковая диаграмма (гистограмма)
Полигон распределения
Сглаженная кривая
Гистограмма - это последовательность столбцов, каждый из которых опирается на один раздельный интервал, а высота столбца – это частота или количество случаев.
Принято распределять горизонтальную шкалу на один раздельный интервал вправо и влево от полученного диапазона. Чтобы гистограмма не получилась сплющенной или вытянутой, выбирают такой масштаб шкалы, чтобы ее ширина составляла 1 2/3 высоты. Середина столбца совмещается с срединой интервала, на практике ее изображают в форме контура, опуская вертикальные линии.
Полигон распределения – это та же гистограмма, но линии соединяют середины столбцов каждого разрядного интервала. Так как на разрядах справа и слева от разрядов распределения частот, частота имеет нулевое значение, поэтому полигон распределения продолжают до горизонтальной оси в середине интервала ниже меньшей оценки и выше высшей оценки.
Огива производится по точкам максимально приближенно без углов или острых фигур, ее называют кривой процентелей. Точки, определяющие кривую процентелей расположены по горизонтали у верхней границы каждого раздела. Огива проходит путь от 0 до 100%. При рисовании огивы надо следить за тем (особенно при малом числе объектов), чтобы, когда мы сглаживаем кривую, над ней оставались бы столько же точек, сколько и под ней. При отсутствии любых графических средств можно создать гистограмму на пишущей машинке в виде полосчатой диаграммы.
Гистограмма наиболее легка для восприятия и используется в тех случаях когда всего одно распределение. Если надо сравнить два и более распределений, используют полигон, чтобы избежать запутанной картины.
Огива дает возможность оценить квантили, медианы и другие характеристики точки. Удобно сравнивать несколько групп данных на одном графике.
Ошибки при использовании графиков
при создании графика не определяли положение нулевой точки;
представили значения в виде площадей в том случае, когда их надо было отражать линейно;
при использовании небольшого количества объектов сделали вывод относительно всей совокупности.
Правила графического оформления
Вся структура графика предполагает его чтение слева на право, вертикальные шкалы – снизу вверх;
На вертикальной шкале разместить нулевую отметку;
Если нулевая линия вертикальной шкалы не перпендикулярна по отношению к графику, то нулевая линия должна быть показана с помощью горизонтальной оси.
Пороговые точки на шкалах желательно выделить размером или цветом, но если речь идет о временном интервале, предпочтительно не указывать начальной и конечной точек. Подобрать такой масштаб, чтобы кривые линии резко отличались от прямых, желательно включить в график цифровые данные и изображение формулы, расположив их в правом верхнем углу, при необходимости использовать ясные полные заголовки и подзаголовки, как для самой диаграммы, так и для ее осей.
Меры центральной тенденции – первый момент, характеризующие данные
При исследовании массивов данных мы чаще всего оперируем величинами, характеризующими этот массив, именно по ним делаем вывод обо всей совокупности данных. К таким характеристикам относятся меры центральной тенденции, то есть значение наиболее часто встречающееся в данной совокупности. Этих мер существует несколько:
мода – это такое значение во множестве наблюдений которое встречается наиболее часто. Сложность в том, что редкая совокупность имеет единственную моду. (Например: 2, 6, 6, 8, 9, 9, 9, 10 – мода = 9).
Соглашения по поводу моры
Если все значения в группе встречаются одинокого часто, считают, что у данной группы, моды нет.
Когда два соседних значения имеют одинаковую частоту и эти частоты больше любых других частот в группе, то модой считают среднее от этих двух значений.
Если два несмежных значения имеют равную и наибольшую в данной группе частоту, то у этой группы есть две моды, такая группа называется бимодальной. Бимодальной называется группа и в том случае, если эти две черты не совсем равны. В таких случаях договорились различать большую и малую моду и во всей группе, наряду с одной большой модой может быть несколько меньших мод.
медиана
– это 50-тый процентиль в группе данных.
>
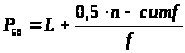 >
>
среднее
(среднеарифметическое
или выборочное среднее) – это сумма
всех значений, разделенная на их
количество. >
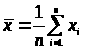 >.
>.
Мода наиболее просто вычисляется и при большом количестве измерений достаточно стабильна и близка к медиане и среднему. Медиана вычисляется по сложнее, особенно легко при ранжированных данных. В больших массивах предлагается сначала сгруппировать их, а потом вычислять медиану. Для определения моды и медианы не требуется знание всех остальных значений.
На определение среднего влияют значения всех изменений.
При наличии интервалов в значении, формула для среднего принимает вид:
>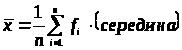 >
>
Свойства среднего
1.
Сумма всех n-отклонений
от значения среднего должно быть равно
нулю, то есть: >
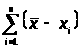 >
>
2. Если константу прибавить к каждому значению, то среднее увеличивается на ту же константу.
3. Если каждое значение умножить на константу, то среднее то же будет умножено на эту константу.
4. Сумма
квадратов отклонений значений от их
среднего меньше суммы квадратов
отклонений от любой другой точки, то
есть: >
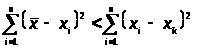 >
>
Средняя медиана и мода для объединенных групп
>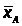 >
- среднее
для каждого класса, >
>
- среднее
для каждого класса, >
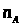 >
- количество учащихся
>
- количество учащихся
Среднее общее группы:
>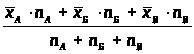 >
>
Для определения моды и медианы объединенной группы необходимы конкретные значения измерений.
Мода – это такое число в группе, с которым совпадает наибольшее количество значений в группе.
Медиана – это такая точка на числовой оси, для которой сумма абсолютных значений разности всех значений меньше суммы разностей для любой другой точки. Если именно так определять понятие ошибки, то медиана дает минимальную ошибку. Если же ошибка определяется как сумма квадратов разностей, то минимальную ошибку дает среднее.
Выбор меры центральной тенденции
В малых группах мода очень нестабильна;
На медиану не влияет величины очень больших и очень малых значений;
На величину среднего влияет каждое значение;
Некоторые множества данных не имеют меры центральной тенденции. Такая ситуация близка к бимодальной гистограмме или U-образной;
Центральная тенденция групп, содержащая крайние значения наилучшим образом представляется в том случае, если гистограмма унимодальна;
Если гистограмма симметрична и унимодальна, то средняя мода и медиана совпадают.
Другие меры центральной тенденции
Среднее
геометрическое: >
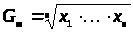 >; Среднегармоническое:
>
>; Среднегармоническое:
>
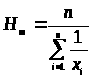 >
>
Меры изменчивости – второй момент характеризующий данные
Для оценки меры неоднородности (разброса, изменчивости), в группе вводят специальные меры, с помощью которых после их исследования можно уменьшить изменчивость данных. Первая из мер изменчивости называется размахом.
Размах – это разность максимального и минимального значений в группе.
Включающий
размах – это разность между естественной
верхней границей интервала, включая
наибольшее значение, и естественной
нижней границей, включая наименьшее
значение интервала. >
 >.
Включающий размах отличается от
исключающего на единицу.
>.
Включающий размах отличается от
исключающего на единицу.
Размах от 90-го до 10-го процентеля: D = P>90> – P>10> . Эта мера более стабильна, чем предыдущая, так как на нее влияет множество значений.
Полу-междуквантильный
размах: >
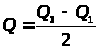 >,
Q
используется в распределениях, которые
симметричны относительно медианы и
среднего, для корректировки границ.
>,
Q
используется в распределениях, которые
симметричны относительно медианы и
среднего, для корректировки границ.
Дисперсия.
Каждая из предыдущих мер возрастает с
ростом рассеяния и уменьшается
однородностей. Дисперсию, в отличие от
предыдущих мер, используют при вычислении
каждого из полученных измерений.
Вычисляются значения отклонений >
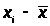 >
и чтобы при суммировании >
>
и чтобы при суммировании >
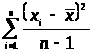 >не
потерять величины этих отклонений,
разница возводится в квадрат, поскольку
мы оцениваем отклонение каждого
измерения, делим на количество измерений.
Обозначается дисперсия как >
>не
потерять величины этих отклонений,
разница возводится в квадрат, поскольку
мы оцениваем отклонение каждого
измерения, делим на количество измерений.
Обозначается дисперсия как >
 >.
>.
>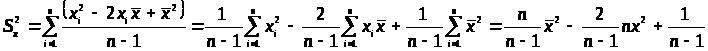 >
>
Для вычисления дисперсии не нужно вычислять среднее.
Дисперсия
при сгруппированных данных вычисляется
по такой же формуле, но >
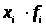 >
>
>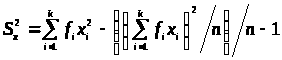 >
>
i
изменяется от 1 до k,
где k –
количество разных значений >
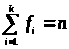 >.
>.
Стандартное
отклонение: >
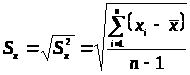 >
>
Для
унимодальных симметричных распределений
почти 70% значений лежит в интервале >
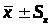 >.
>.
Свойства дисперсии:
1. Влияние на дисперсию увеличения каждого значения на какую либо константу:
>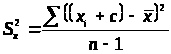 >,
после выполнения математических операций
убеждаемся, что дисперсия не изменяется.
>,
после выполнения математических операций
убеждаемся, что дисперсия не изменяется.
2. Изменение дисперсии при умножении каждого исходного значения на константу:
>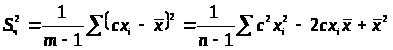 >,
то есть дисперсия увеличивается на
квадрат константы.
>,
то есть дисперсия увеличивается на
квадрат константы.
3. Дисперсия объединенной группы:
>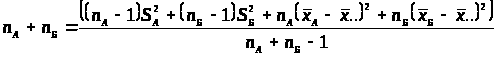 >
>
где:
> >
>
>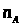 >
- количество
значений группы А, для Б аналогично
>
- количество
значений группы А, для Б аналогично
>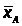 >
- среднее
группы А, для Б аналогично
>
- среднее
группы А, для Б аналогично
Среднее отклонение – это совокупность отклонений каждого значения от среднего, взятого по модулю:
>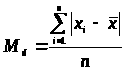 >
>
Очень проста в вычислениях, но редко используется, ввиду того, что нет теоретического обоснования.
Стандартизованные данные
Часто появляется потребность оценить положение какого-либо конкретного значения по отношению к среднему в единицах стандартного отклонения
>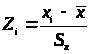 >
>
Любое множество данных можно преобразовать в такое множество, у которого среднее равно нулю, а стандартное отклонение равно единице.
>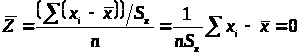 >
>
>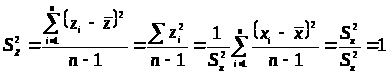 >
>
Значение стандартизованных данных Z позволяют преобразовать множество x в произвольную шкалу с удобными характеристиками среднего и стандартизованного отклонения. Сами оценки Z могут быть отрицательными или содержать дроби. Мы избавимся от этих шероховатостей, умножая стандартизованные данные на константу и прибавляем к ним константу.
сz – будет иметь стандартное отклонение
>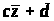 >,
где с, d
– константы –
будут иметь среднее равное d.
>,
где с, d
– константы –
будут иметь среднее равное d.
Третий момент
Асимметрия – это свойство распределения частот. На практике симметричные полигоны и гистограммы не встречаются и чтобы выявить и оценить степень асимметрии, вводят следующую меру:
>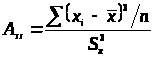 >
>
В единицах стандартного отклонения асимметрия равна:
>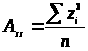 >
>
Асимметрия бывает положительной и отрицательной. Положительная сдвигается влево, а отрицательная – вправо.
Чтобы упростить вычисление A>ss> можно использовать следующую формулу:
>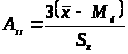 >
>
Асимметрия в этом уравнении принимает значения от –3 до +3
Четвертый момент
>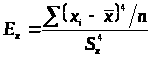 >
>
Эксцесс – это мера крутости кривой распределения. Унимодальная кривая распределения может быть островершинной, плосковершинной, средне вершинной.
Эксцесс для стандартных данных:
>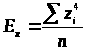 >
>
-
Характер распределения
Величина эксцесса
Нормальное
Островершинное
Плосковершинное
3
больше 3 и может быть очень большим
больше нуля, но меньше 3
Эти четыре момента составляют набор особенностей распределения при анализе данных.
Нормальное распределение
Нормальное распределение лучше всего описывается кривой созданной ДеМуавром по следующей формуле:
>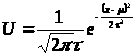 >
>
где U – высота кривой над осью x, t и μ – числа, которые определяют положение кривой относительно числовой оси и регулируют ее размах. Для μ=0, t=1 график принимает вид:
 Эта
кривая при μ=0,
t=1
получила статус стандарта, ее называют
единичной
нормальной кривой,
то есть любые собранные данные стремятся
преобразовать так, чтобы кривая их
распределения была максимально близка
к этой стандартной кривой. Созданы
статистические таблицы со значениями
площади под единичной нормальной кривой
влево от любой точки на оси z
в (-3; 3). Общая площадь под кривой равна
1. И все остальные площади рассматривают
как процент от целого.
Эта
кривая при μ=0,
t=1
получила статус стандарта, ее называют
единичной
нормальной кривой,
то есть любые собранные данные стремятся
преобразовать так, чтобы кривая их
распределения была максимально близка
к этой стандартной кривой. Созданы
статистические таблицы со значениями
площади под единичной нормальной кривой
влево от любой точки на оси z
в (-3; 3). Общая площадь под кривой равна
1. И все остальные площади рассматривают
как процент от целого.
Свойства нормальных кривых:
Семейство нормальных кривых включают в себе все кривые, которые можно получить по данной формуле, отличающиеся друг от друга только парой значений t и μ .
1. 68% площади
лежит в интервале >
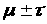 >
>
2. 95% площади
лежит в интервале >
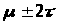 >
>
3. 99,7% площади
лежит в интервале >
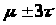 >
>
Если x
имеет нормальное распределение со
средним μ
и стандартным отклонение t,
то z равное
>
 >
характеризуется распределением со
средним равным нулю и стандартным
отклонением равным 1. Площадь между
двумя значениями x
в нормальном распределении равна площади
между ux
стандартизованными величинами в
единичном нормальном распределении.
Нормализованную кривую изобрели для
решения задач теории вероятности, но
оказалось на практике, что она отлично
аппроксимирует распределение черт при
большом числе наблюдений для множества
переменных. Можно предположить, сто не
имея материальных ограничений на
количество объектов и время проведения
эксперимента, статистическое исследование
приводило к нормально кривой.
>
характеризуется распределением со
средним равным нулю и стандартным
отклонением равным 1. Площадь между
двумя значениями x
в нормальном распределении равна площади
между ux
стандартизованными величинами в
единичном нормальном распределении.
Нормализованную кривую изобрели для
решения задач теории вероятности, но
оказалось на практике, что она отлично
аппроксимирует распределение черт при
большом числе наблюдений для множества
переменных. Можно предположить, сто не
имея материальных ограничений на
количество объектов и время проведения
эксперимента, статистическое исследование
приводило к нормально кривой.
Двумерное нормальное распределение
Если при исследовании появляется вопрос о связи между двумя переменными для одного и того же объекта (например, рост и интеллект) мы говорим о двумерных связях и результаты эксперимента находят свое отражение в двумерном распределении частот.
Уравнение поверхности называется двумерным нормальным распределением (гладкая непрерывная колоколообразная поверхность)
Характеристики нормального распределения
Распределение значений x без учета значений y есть нормальное распределение;
Распределение значений y без учета значений x, тоже нормальное распределение;
Для
каждого фиксированного значения x
значение y
дают нормальное распределение с
дисперсией >
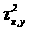 >;
>;
Для
каждого фиксированного значения y
значение x
распределяется
нормально с дисперсией >
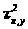 >;
>;
Среднее значения y для каждого отдельного значения x ложатся на переменную.
Меры изменчивости
При решении вопроса о наличии взаимосвязи (корреляции) между двумя переменными, руководствуются несколькими коэффициентами. Связь, выраженная графически, называется диаграммной рассеивания, где x – оценка IQ, y – оценка теста по математике.
Положение
каждого объекта на диаграмме распределения
определяется парой значений x>i>,
y>i>
и выражаются по отношению к мере
центральной тенденции величинами >
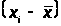 >,
>
>,
>
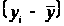 >.
Если объект имеет высокие показатели
по обеим переменным, то эти величины
получаются большими и положительными,
в противном случае, если x>i>,
y>i>>
> малы, то
разность большой и отрицательной.
>.
Если объект имеет высокие показатели
по обеим переменным, то эти величины
получаются большими и положительными,
в противном случае, если x>i>,
y>i>>
> малы, то
разность большой и отрицательной.
В дальнейшем
будем говорить о произведении этих
разностей и в том случае когда наблюдается
прямая связь между этими переменными,
произведение будет большим и положительным,
следовательно такой же будет и сумма
этих произведений >
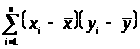 >.
>.
В случае обратной связи, когда большим значениям y>i> соответствуют малые значения x>i>> >и наоборот, в этом случае произведение разностей будет большим и отрицательным и сумма разностей также будет большой и отрицательной.
Если между переменными не наблюдается какой-либо связи , количество положительных и отрицательных произведений примерно рано и сумма их близка к нулю. Таким образом большая положительная сумма – жесткая прямая зависимость; большая отрицательная сумма – сильная обратная зависимость; близость к нулю – отсутствие зависимости.
Недостатком этой меры является то, что ее величина зависит от числа пар переменных x участвующих в расчетах.
Чтобы избежать связь независимого состояния V групп, мы усредняем эти значения:
>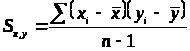 >
- ковариация
>
- ковариация
Частный случай, ковариация переменной с самой сабой – дисперсия
Чтобы избавить меру связи от отклонений двух групп значений:
>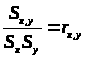 >
- коэффициент
кореляции Пирсона или произведение
моментов.
>
- коэффициент
кореляции Пирсона или произведение
моментов.
>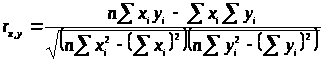 >
>
Значение коэффициента Пирсона не может выйти за границы интервала (-1; 1).
Влияние линейного преобразования переменных на коэффициент кореляции
Вместо x>i> вводим в формулу bx+ a, где a, b – коэффициенты, для y>i> вводим в формулу dy+ c, где c, d – коэффициенты.
>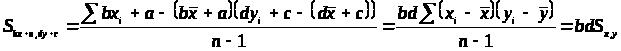 >
>
>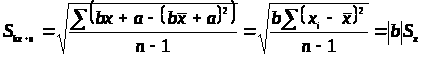 >
>
>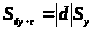 >
>
>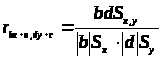 >
>
Вопрос о кореляции между переменными будучи решен положительно не означает наличия более общего вида связи (заработная плата учителям и количество поступивших в ВУЗы после окончания школы). Если мы проводим идентификацию групп с различным средним, наличие кореляции не исключено, но возможно другое объяснение взаимосвязи, чем вытекающее их эксперимента. Отсутствие связи при нулевом коэффициента Пирсона означает всего лишь отсутствие линейной связи.
Дисперсия суммы и разности переменных
>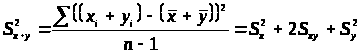 >
>
>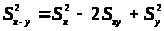 >
>
>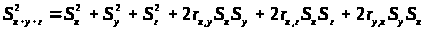 >
>
Предсказание и оценивание
Переменная, которую мы хотим оценить называется зависимой переменной или откликом , обозначим ее через y.
Переменная которую мы используем для оценки называется независимой переменной или фактором, ее обозначим через x.
Конкретная
характеристика (переменная x)
имеющаяся в нашем распоряжении, позволяет
получить до проведения эксперимента
значение y,
зависимой переменной. Мы получаем >
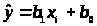 >
используя x>i>
и коэффициенты b>1>
и b>0>.
>
используя x>i>
и коэффициенты b>1>
и b>0>.
Даже при
наилучшем линейном предсказании,
предсказание >
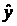 >
будет отличаться от реального y>i>
на какую-то величину, которую мы назовем
ошибкой
оценки
и обозначим e>i>:
>
будет отличаться от реального y>i>
на какую-то величину, которую мы назовем
ошибкой
оценки
и обозначим e>i>:
>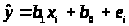 >
>
Точность
предсказания зависит от того, насколько
удачно подобраны коэффициента b>1>
и b>0>.
Критерием успешности подбора коэффициентов
является минимальная величина суммы
квадратов всех ошибок оценки >
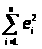 >–
критерий
наименьших квадратов
>–
критерий
наименьших квадратов
Другой
критерий: >
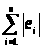 >.
Этот критерий приводит к медианой линии
регрессии. Из уравнения >
>.
Этот критерий приводит к медианой линии
регрессии. Из уравнения >
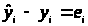 >
следует >
>
следует >
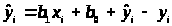 >
>
Исходя из минимизации формулы наименьших квадратов найдем формулы:
>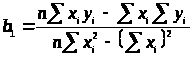 >; >
>; >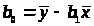 >
>
Наше исследование получается наиболее результативным, если мы предполагаем, что фактор и отклик имеют двумерные нормальные распределения.
Свойства двумерного нормального распределения
1. Выборочные средние отклика (y) для каждого значения x лежат на прямой;
2. Для любого значения x, соответствующие значения y нормально распределены;
3. Для любого
значения x, y
– имеют одинаковую дисперсию >
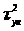 >.
>.
При прогнозировании является ли среднее ошибок оценки подходящей мерой для прогнозирования.
>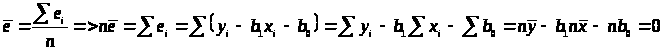 >
>
Средняя ошибка оценки всегда равна нулю. Один из способов доказать этот факт, это выбрать в качестве меры прогнозирования дисперсию ошибки оценки.
Стандартная
ошибка оценки >
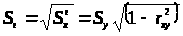 >
>
Стандартную
ошибку оценки применяют для определения
пределов, в окрестности предсказанного
>
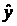 >попадает
фактическое значение y>i>.
>попадает
фактическое значение y>i>.
В приделах S>e> – расположено 69% фактических значений объекта, в приделах 2S>e> – 95%, в приделах 3S>e> – 97,5%.
Связь b>1> и b>0> с другими описательными статистиками
> >
>
>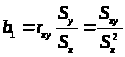 >
>
Если x
и y
распределены по нормальному закону и
имеют одинаковую дисперсию, то >
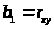 >.
>.
Поскольку
r>xy>>
>не зависит
от S>x>
и S>y>,
b>1>
- принимает максимальное значение при
r>xy>
=1 и минимальное значение при r>xy>
= -1, следовательно b>1
>никогда не
может быть больше >
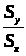 >,
при r>xy>
=1 и не может быть меньше >
>,
при r>xy>
=1 и не может быть меньше >
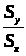 >
при r>xy>
= -1.
>
при r>xy>
= -1.
Если между
переменными отсутствует линейная связь,
b>1>=0
уравнение регрессии сводится к прямой
без наклона, то есть >
 >.
>.
Измерение нелинейной связи между переменными
Для
определения меры нелинейной связи между
переменными используется коэффициент
>
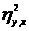 >
>
>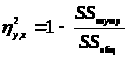 >
>
Эта мера может быть использована и для оценки линейной связи.
Пример вычисления:
|
x/возраст |
10 |
14 |
18 |
22 |
26 |
30 |
34 |
38 |
|
7 |
8 |
9 |
11 |
9 |
8 |
7 |
8 |
|
|
8 |
9 |
10 |
11 |
10 |
9 |
9 |
||
|
9 |
10 |
11 |
12 |
11 |
9 |
10 |
||
|
9 |
11 |
12 |
12 |
10 |
||||
|
10 |
>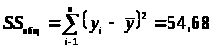 > >
> >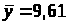 >
>
Находим среднее для каждого возраста и суммируем отношения каждого y>i> от среднего соответствующего группы.
Для 10
- >
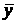 >=8,6;
18 – 9,5; 22 – 11,5; 26 – 10; 90 – 9; 34 – 8,67; 38 – 8.
>=8,6;
18 – 9,5; 22 – 11,5; 26 – 10; 90 – 9; 34 – 8,67; 38 – 8.
>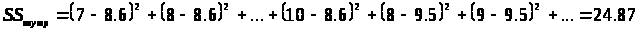 >
>
>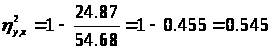 >
>
>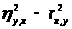 >
- является
мерой нелинейности связи и >
>
- является
мерой нелинейности связи и >
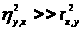 >
>
Другие меры связи
Измерения в дихотомической шкале (например, женат – не женат, мужчина – женщина)
Измерение в дихотомической шкале наименований в предположении нормального распределения. Предполагается, что при более полных, более совершенных измерениях данные распределятся по нормальному закону.
Шкала порядка
Измерение в шкале интервалов или отношений.
 Рассмотренный
ранее коэффициент кореляции Пирсона
соответствует сочетанию J
при измерении исходных данных. Для
описания степени кореляции при других
комбинациях шкал измерений исходных
данных используются следующие меры.
Рассмотренный
ранее коэффициент кореляции Пирсона
соответствует сочетанию J
при измерении исходных данных. Для
описания степени кореляции при других
комбинациях шкал измерений исходных
данных используются следующие меры.
Случай A.
>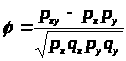 >
>
p>x>> >– доля людей имеющих 1 по x, p>y>> >– доля людей имеющих 1 по y
q>x>> >– доля людей имеющих 0 по x, q>y>> >– доля людей имеющих 0 по y
p>xy> - доля людей имеющих 1 по x и y
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
x |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
|
y |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
x – женат / холост
y – исключенные из учебного заведения / оставшиеся
p>x>> >=0,4167 ; p>y>> >= 0,5 ; q>x>> >=0,5833 ; q>y>> >= 0,5 ; p>xy> =0,333; φ=0,507
Если нет особого интереса к доле p>x>> >и p>y>, дихатомические данные располагают в таблице сопряженности признаков. Пример таблицы сопряженности по приведенным данным
 φ
– определяется
по формуле:
φ
– определяется
по формуле:
>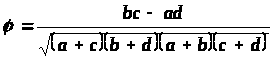 >
>
Коэффициент φ, это тот же коэффициент кореляции Пирсона, но эти данные не похожи на двумерное нормальное распределение, которое мы представляли при вычислении коэффициента Пирсона. Это рассматривается как большое неудобство статистиками.
Случай B.
Удовлетворительного коэффициента для этого случая не существует, рекомендуется исходить из предположения о нормальном распределении данных и вычислять φ в качестве меры связи для этого случая.
Случай C.
Для этого случая подходят коэффициенты, о котором мы расскажем в случае I.
Случай D.
Используется
биссериальный коэффициент кореляции:
>
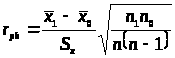 >
>
>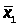 >
- среднее
по x
объектов имеющих 1 по y.
>
- среднее
по x
объектов имеющих 1 по y.
>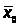 >
- среднее
по x
объектов имеющих 0 по y.
>
- среднее
по x
объектов имеющих 0 по y.
S>x> – стандартное отклонение
Случай E.
Тетрахорический
коэффициент кореляции: >
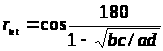 >
>
Более удобно при расчете обращаться к статическим таблицам, содержащим вычисления из этого уравнения. Они составлены при условии, что bc/ad>1. В противном случае таблица содержит ad/bc и величина тетрахорического коэффициента будет отрицательной.
Случай F.
Удовлетворительного коэффициента не разработано, рекомендуется продположить нормальное распределение для x и использовать биссериальный ранговый коэффициент (см. случай G).
Случай G.
Биссериальный
коэффициент: >
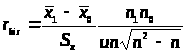 >
>
u – ордината нормального распределения.
Случай H.
Используется
коэффициент ранговой кореляции Спирмана:
>
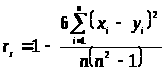 >
>
В том случае, если при измерении встречается связанные ранги, это уравнение не подходит в качестве меры кореляции.
Связанный ранг возникает в том случае, если у некоторых объектов получено одинаковое значение переменной. В этом случае ранги, которые должны были бы получить эти объекты суммируются и делятся на количество объектов и каждый получает, пролученный при вычислении ранг.
До сих пор коэффициенты кореляции представляли из себя или могли быть объяснены в терминах произведения моментов. Коэффициент кореляции, не связвнный с моментами построен Кендаллом и называется τ – Кендалла
>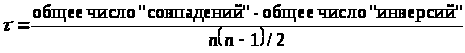 >
>
Случай I.
Для этого случая коэффициенты не разработаны, рекомендуется преобразовать оценки по y в ранги и найти или коэффициент Спирмана или Кендалла
Бисериальная
ранговая кореляция: >
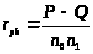 >
>
P – сумма всех совпадений; Q – сумма всех инверсий;
n>0>> >– число объектов при нулевой дихотомии; n>1>– число объектов при единичной дихотомии.