Системы 2-х, 3-х линейных уравнений, правило Крамера
Системы 2-х , 3-х линейных уравнений, правило Крамера
ОГЛАВЛЕНИЕ.
1.Краткая теория .
2. Методические рекомендации по выполнению заданий.
3.Примеры выполнения заданий.
4.Варианты заданий.
5.Список литературы.
1. КРАТКАЯ ТЕОРИЯ .
Пусть дана система линейных уравнений
>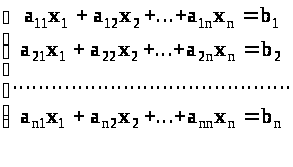 >
(1)
>
(1)
Коэффициенты a>11>,>12>,..., a>1n>, ... , a>n1 >, b>2> , ... , b>n> считаются заданными .
Вектор -строка íx>1> , x>2> , ... , x>n> ý - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=çAê=ça >ij> ç, составленный из коэффициентов при неизвестных , называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи.
a).
Если D¹0,
то система (1) имеет единственное решение,
которое может быть найдено по формулам
Крамера : x>1>=> >,
где
>,
где
определитель n-го порядка D>i> ( i=1,2,...,n) получается из определителя системы путем замены i-го столбца свободными членами b>1 >, b>2 >,..., b>n>.
б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо несовместна ,т.е. решений нет.
2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
>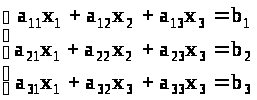 >
(2).
>
(2).
1. В данной
системе составим определитель >
 >
и вычислим.
>
и вычислим.
2. Составить и вычислить следующие определители :
>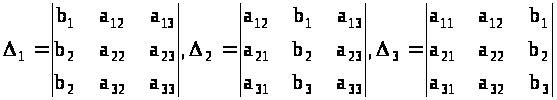 >
.
>
.
3. Воспользоваться формулами Крамера.
> >
>
3. ПРИМЕРЫ.
1. >
 >.
>.
> >
>
>
 >
>
>
>
 >
>
> >
>
>
>
 >.
>.
Проверка:
> >
Ответ:
( 3 ; -1 ).
>
Ответ:
( 3 ; -1 ).
2. >
 >
>
> >
>
> >
>
> >
>
Проверка:
>
 >
>
Ответ: x=0,5 ; y=2 ; z=1,5 .
4. ВАРИАНТЫ ЗАДАНИЙ.
ВАРИАНТ 1.
Решить системы:
> >
>
ВАРИАНТ 2.
Решить системы:
> >
>
ВАРИАНТ 3.
Решить системы:
> >
>
ВАРИАНТ 4.
Решить системы:
> >
>
ВАРИАНТ 5.
Решить системы:
>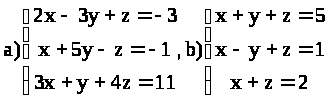 >
>
ВАРИАНТ 6.
Решить системы:
> >
>
ВАРИАНТ 7.
Решить системы:
> >
>
ВАРИАНТ 8.
Решить системы:
>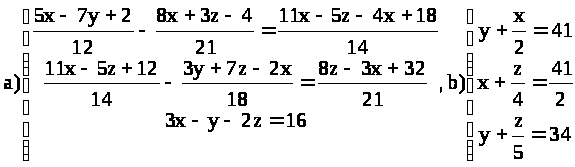 >
>
Литература
1. Г.И. КРУЧКОВИЧ. “Сборник задач по курсу высшей математике”, М. “Высшая школа”, 1973 год.
2. В.С. ШИПАЧЕВ. “Высшая математика”, М. “Высшая школа”, 1985 год.