Механические колебания в дифференциальных уравнениях (работа 2)
Механические колебания в дифференциальных уравнениях
Реферат Выполнил: студент гр. МХТ-02 Казаков Василий Васильевич
Магнитогорский государственный технический университет им. Г.И. Носова
Магнитогорск 2003
Колебаниями называются процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качания маятника часов, переменный электрический ток и т.д. При колебательном движении маятника изменяется координата центра масс, в случае переменного тока колеблются напряжение и сила тока. Физическая природа колебаний может быть разной, однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Рассмотрим механические колебания.
Гармонические колебания.
Гармоническими колебаниями называются колебания, при которых изменяющаяся величина изменяется по закону синуса (косинуса).
Пусть груз весом Р подвешен на вертикальной
пружине, длина которой в естественном
состоянии равна >
>.
Груз слегка оттянут книзу и затем
отпущен. Найдем закон движения груза,
пренебрегая массой пружины и сопротивлением
воздуха.
Решение
Направим ось Ох вниз по вертикальной прямой, проходящей через точку подвеса груза. Начало координат О выберем в положении равновесии груз, то есть в точке, в которой вес груза уравновешивается силой натяжения пружины.
Пусть l
означает удлинение пружины в данный
момент, а l>ст>—статическое
удлинение, т.е. расстояние от конца
нерастянутой пружины до положения
равновесия. Тогда l=l>ст>+х,
или l-l>ст>=х.
Дифференциальное уравнение получим из второго закона Ньютона: F=ma, где m=P/g—масса груза а—ускорение движения и F—равнодей-ствующая приложенных к грузу сил. В данном случае равнодействующая слагается из силы натяжения пружины и силы тяжести.
По закону Гука сила натяжения пружины пропорциональна её удлинению: F>упр>=-сl, где с – постоянный коэффициент пропорциональности называемый жесткостью пружины.
>
>
Так как в положении равновесия сила равновесия сила натяжения пружины уравновешивается весом тела, то P= сl>ст>. Подставим в дифференциальное уравнение выражение Р и заменим l-l>ст> через х, получится уравнение в виде:
>
>
или, обозначив с/m через k2,
>
>
(1)
Полученное уравнение определяет так называемые свободные колебания груза. Оно называется уравнением гармонического осциллятора. Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение:
>
>
имеет мнимые корни >
>,
соответственно этому общее решение
>
>
Для выяснения физического смысла решения
удобнее привести его к другой форме,
введя новые произвольные постоянные.
Умножив и разделив на >
>,
получим:
>
>
Если положить
>
>
>
>
>
>
то
>
>
(2)
График гармонических колебаний имеет вид:
Таким образом, груз совершает гармонические колебания около положения равновесия.
Величину А называют амплитудой
колебания, а аргумент >
>
— фазой колебания. Значение фазы при
t=o
т.e.
величина >
>,
называется начальной фазой колебания.
Величина >
>
есть частота колебания. Период колебания
>
>
и частота k
зависят только от жесткости пружины и
от массы системы. Так как с = Р/l>ст>
= mg/l>ст>,
то для периода можно получить также
формулу:
>
>
Скорость движения груза получается дифференцированием решения по t:
>
>
Для определения амплитуды
и начальной фазы необходимо задать
начальные условия. Пусть, например, в
начальный момент t
= 0 положение груза x=x>0>
и скорость u=u>0>.
Тогда >
>
>
>,
откуда
>
>,
>
>
Из формул для амплитуды и начальной фазы видно, что в отличие от частоты и периода собственных колебаний они зависят от начального состояния системы. При отсутствии начальной скорости (u>0>=0) амплитуда А=х>0>, а начальная фаза a=p/2 и, таким образом,
>
>
или >
>
Затухающие колебания.
Затухающими колебаниями называются колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшают-ся. Найдем закон движения груза в условиях предыдущей задачи, но с учетом сопротивления воздуха, которое пропорционально скорости движения.
Решение
К силам, действующим на
груз, прибавляется здесь сила сопротивления
воздуха >
>
(знак минус показывает, что сила R
направлена противоположно скорости
u).
Тогда дифференциальное
уравнение движения в проекции на ось
Ox
имеет вид
>
>
или если положить >
>,
>
>,
то
>
>
(3)
Это уравнение также является линейным однородным уравнением второго порядка с постоянными коэффициентами. Его характеристическое уравнение:
>
>
имеет корни
>
>
(4)
Характер движения целиком
определяется этими корнями. Возможны
три различных случая. Рассмотрим сначала
случай, когда >
>.
Это неравенство имеет место, когда
сопротивление среды невелико. Если
положить >
>,
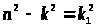то корни (4) имеют вид >
>.
Тогда общее решение можно записать в
виде
>
>
или, преобразовав, умножая и деля на >
>,
получим:
>
>
положим, что
>>
>
>
>
>,
тогда
>
>
(5)
График зависимости отклонения от положения равновесия от времени имеет вид:
Если заданы начальные
условия: >
>
при t
= 0, то можно определить А и a.
Для этого находим
>
>
и подставляем t
= 0 в выражения для >
>и
>
>
получим систему уравнений
>
>
Разделелив обе части второго уравнения на соответствующие части первого получим
>
>
откуда
>
>
или >
>
а >
>
Так как
>
>
то
>
>
Решение (5) показывает, что
имеют место затухающие колебания.
Действии-тельно, амплитуда колебания
>
>
зависит от времени и является монотонно
убывающей функцией, причем >
>
при >
>.
Период затухающих колебаний определяется по формуле
>
>
Моменты времени, в которые
груз получает максимальное отклонение
от начала координат (положения равновесия),
образуют арифметическую прогрессию с
разностью, равной полупериоду Т/2.
Амплитуды затухающих колебаний образуют
убывающую геометрическую прогрессию
со знаменателем, равным >
>
или >
>.
Эта величина называется декрементом
затухания и обычно обозначается буквой
D.
Натуральный логарифм декремента lnD
= - пТ/2 называется логарифмическим
декрементом затухания.
Частота колебаний >
>в
этом случае меньше, нежели в предыдущем
(>
>),
но, как и там, не зависит от начального
положения груза.
Если сопротивление среды
велико и >
>,
то, положив >
>,
получим корни (4) в виде >
>
Так как >
>,
то оба корня отрицательны. Общее решение
уравнения в этом случае имеет вид
>
>
(6)
Отсюда видно, что движение
апериодическое и не имеет колебательного
характера. Аналогичный характер будет
иметь движение и в случае >
>,
когда общее решение имеет вид
>
>
(7)
Легко заметить, что в обоих
последних случаях при >
>
имеем >
>.
Если заданы начальные
условия >
>
и >
>,
то в случае, когда >
>,
имеем >
>,
а >
>.
Решая эту систему относительно >
>
и >
>,
получим
>
>,
>
>
и, следовательно
>
>
>
>
В случае же, когда >
>,
получаем >
>,
>
>
и следовательно,
>
>
Вынужденные колебания без учета сопротивления среды.
Вынужденными колебаниями называют колебания, вызванные внешней периодической возмущающей силой.
Пусть груз весом Р подвешен
на вертикальной пружине, длина которой
в ненагруженном состоянии равна >
>.
На груз действует периодическая
возмущающая сила >
>
где Q
и р — постоянные. Найдем закон движения
груза, пренебрегая массой пружины и
сопротивлением среды.
Решение
Как и для гармонических колебаний, получаем уравнение
>
>
Полагая, как и прежде, >
>
и, кроме того, >
>
перепишем уравнение в виде
>
>
(8)
Это—неоднородное линейное
уравнение второго порядка с постоянными
коэффициентами, причем однородным
уравнением, соответствующим уравнению
(8), является (1). Поэтому >
>;
остается найти х. Если предположить,
что >
>,
то частное решение х, нужно искать в
виде >
>,
где М и N
— коэффициенты, подлежащие определению.
Итак,
>
>>
>
Производя вычисления, получаем
>
>
>
>
откуда М=0 и >
>
Полученное таким образом частное решение
>
>
(9)
определяет так называемые
вынужденные колебания, созданные
возмущаю-щей силой >
>.
Вынужденные колебания, имеют тот же
период, что и возмущающая сила, совпадают
с ней по фазе (т. е. имеют одинаковую
начальную фазу) при k>p,
либо отличаются на p,
если k<p,
т. е. если N<0.
Закон движения представляется общим решением
>
>.
(10)
Оно слагается из собственно вынужденных колебаний (9), которые определяются внешней возмущающей силой, и собственных колебаний (2), обусловленных исключительно внутренними причинами: жесткостью пружины и массой груза.
Если заданы начальные
условия: >
>
и >
>,
то можно определить произвольные
постоянные А и u.
Для этого продифференцируем функцию
(10):
>
>
и подставим в выражения
х и >
>
значение аргумента t
= 0; получим систему уравнений
относительно A
и a:
>
>
Преобразуем её так:
>
>
возведем в квадрат обе части каждого из этих уравнений и сложим. Тогда
>
>
Для нахождения a разделим обе части первого уравнения на соответствую-щие части второго; получим
>
>
откуда
>
>
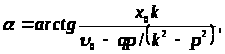при этом >
>,
>
>
Итак, искомым частным решением, удовлетворяющим заданным начальным условиям, является функция
>
>
или
>
>
Частное решение (9),
характеризующее собственно вынужденные
колебания, было получено в предположении,
что >
>,
т. е. что частота внешней силы не совпадает
с частотой собственных колебаний. Если
же >
>,
то дело будет обстоять совсем иначе.
Действительно, уравнение (8) можно
переписать теперь в виде
>
>
(11)
Частное решение следует искать в форме
>
>,
где М и N — коэффициенты, подлежащие определению. Итак,
>>>
>
откуда получаем >
>,
>
>,
и следовательно, частное решение имеет
вид
>
>
Общее решение в этом случае
>
>
(12)
Найдем >
>
и подставим в выражения х и >
>
значение t=0;
получим
>
>
>
>
>
>
или >
>
Из последних двух равенств находим
>
>,
>
>
откуда
>
>
>
>
>
>
Перепишем общее решение так:
>
>
тогда искомое частное решение, удовлетворяющее заданным начальным условиям, запишется в виде.
>
>
Выражение (12) показывает,
что амплитуда вынужденных колебаний >
>
в этом случае может стать неограниченно
большой даже тогда, когда q
невелико. Иначе говоря, возможно получение
сколь угодно больших амплитуд при малых
возмущающих силах. Это явление называется
резонансом. Таким образом, резонанс
наступает тогда, когда частота возмущающей
силы совпадает с частотой собственных
колебаний.
Впрочем, в действительности
точное совпадение этих частот не является
необходимым. Выражение (9) для вынужденного
колебания показывает, что при близости
частот амплитуда >
>
может быть очень большой, хотя и
ограниченной при фиксированных частотах
k
и р. Возможностью создания колебаний с
значительной амплитудой часто пользуются
в различных усилителях, например в
радиотехнике. С другой стороны, в большом
числе случаев появление больших амплитуд
является вредным, ибо может приводить
к разрушению конструкций (скажем, мостов
или перекрытий).
Вынужденные колебания с учетом сопротивления среды.
Найдем закон движения груза в условиях предыдущей задачи с учетом сопротивления среды, пропорционального скорости движения.
Решение
Как и выше, имеем
>
>
или положив>>,
>
>и
>
>
>
>
(13)
Однородным уравнением,
соответствующим (13), является уравнение
(3) с корнями характеристического
уравнения (4). Предположим, что сопротивление
среды невелико, т. е. >
>.
При этом общее решение однородного
уравнения имеет вид (5):
>
>
где >
>.
Это решение определяет свободные
колебания, которые будут затухающими.
Для отыскания вынужденных колебаний
ищем частное решение в виде
>>
Имеем:
>
>
>
>
Сравнивая коэффициенты, получаем систему
>
>
Так как
>
>
>
>
>
>>
>
>
>
>
>
>
>>>>
>
то
>
>
и >
>
и мы находим частное решение
>
>
Преобразуем выражение >
>
следующим образом:
>
>.
Обозначив
>
>
>
>
>
>
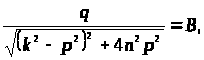(14)
перепишем >
>
виде
>
>
(15)
Выражение
>
>
(16)
носит название сдвига фазы. Общее решение, как и в предыдущей задаче, слагается из свободных колебаний [см. формулу (5)] и собственно вынужденных колебаний (15):
>
>
(17)
Первое слагаемое, как было
сказано выше, определяет затухающие
колебания, которые, особенно при большом
>
>,
довольно скоро становятся мало ощутимыми.
Что касается вынужденных колебаний
(15), то их амплитуда (14) не зависит от
времени и пропорциональна амплитуде Q
периодического возмущения, так как >
>.
Она отличается от q
множителем
>
>
(18)
характеризующим зависимость амплитуды вынужденного колебания от частоты возмущающей силы.
Определим максимум этой амплитуды. Для этого найдем производную функции (18)
>
>
Положив >
>,
получим уравнение >
>
(случай р = 0 отбрасывается как
невозможный), корень которого
дает частоту внешних сил:
>
>
при которой, как показывает проверка достаточных условий экстремума, амплитуда вынужденных колебаний будет максимальной. Максимальное значение амплитуды равно
>
>
(19)
Формула (19) показывает, что амплитуда колебаний тем больше, чем меньше п. При малых п частота р близка к частоте собственных колебаний k.
Решение (15) существует всегда, когда
>
>
В случае >
>получаем
p=k
и n=
0, и уравнение (13) превращается в уравнение
(11). Здесь вновь наступает явление
резонанса, при котором, как было
рассмотрено выше, вынужденные колебания
имеют вид (12).
Список литературы
Для подготовки данной применялись материалы сети Интернет из общего доступа