Операторные уравнения (работа 1)

Операторные уравнения

Выпускная квалификационная работа

Выполнила студентка V курса математического факультета Кощеева Анна Сергеевна

Вятский Государственный Гуманитарный университет (ВятГГУ)

Киров 2005

Введение

Функциональный анализ – мощное средство для решения математический задач, возникающих в реальных ситуациях, он имеет множество приложений в различных областях математики, его методы проникают в смежные технические дисциплины.

Многие задачи математической физики, теории упругости, гидродинамики сводятся к отысканию решения дифференциального линейного уравнения, что, в свою очередь, приводит к задаче отыскания решения уравнения Аx = y с линейным оператором А. В данной работе рассмотрены два метода решения операторных уравнений.

Цель данной работы: рассмотреть основы теории линейных операторов и методы решения операторных уравнений – метод малого параметра и метод продолжения по параметру, показать применение этих методов к решению задач.

Изучив имеющийся материал по данной теме, я поставила перед собой следующие задачи:

раскрыть некоторые основы теории линейных операторов, необходимые для освоения методов решения операторных уравнений;

проиллюстрировать на конкретных примерах способы решения операторных уравнений и дать пояснения по ходу решения конкретных задач.

Так как выделение из функционального анализа его прикладной части, содержащей конструктивные методы получения решений задач, преследует методическую цель – сделать эти методы доступнее тем, кто занимается приложениями математики. Поэтому данная работа разделена на две главы, в первой содержатся необходимые теоретические обоснования способов решения операторных уравнений и суть обоих методов, а во второй – решения конкретных задач.

Глава 1. Операторные уравнения

§1.Определение линейного оператора

Пусть X и Y – линейные пространства, оба вещественные или оба комплексные.

Оператор А: X → Y с областью определения D(А) называется линейным, если

А(λ1x1 + λ2x2) = λ1А(x1) + λ2А(x2)

для любых x1,x2 Î D и любых скаляров λ1 и λ2.

Пусть X и Y – нормированные пространства и А: X → Y, где А – линейный оператор, всюду заданный в X (т.е. D(А) = X).

Оператор А называется непрерывным в точке x0 Î X, если Аx → Аx0 при x → x0. Но судить о непрерывности линейного оператора в различных точках x0 Î X можно по непрерывности его в нуле пространства X.

Теорема 1. Пусть линейный оператор А всюду задан в банаховом пространстве X и со значениями в банаховом пространстве Y непрерывен в точке 0 Î X; тогда А непрерывен в любой точке x0 Î X.

Доказательство. Рассмотрим равенство Аx – Аx0 = А (x – x0). Если x → x0, то z = x – x0 → 0. По непрерывности в нуле Аz → 0, но тогда Аx – Аx0 → 0, что и требовалось доказать.

Линейный оператор А называется непрерывным, если он непрерывен в точке x = 0.

Пусть S1(0) – замкнутый шар ||x|| ≤ 1 в банаховом пространстве X.

Будем называть линейный оператор А: X → Y ограниченным, если он ограничен на единичным шаре S1(0), т.е. если ограничено множество

{ ||Аx||, ||x|| ≤ 1}.

Согласно определению, если А ограничен, то существует постоянная с > 0 такая, что для любых x с ||x|| ≤ 1 справедливо неравенство

||Аx|| ≤ с (1)

Теорема 2. А ограничен тогда и только тогда, когда справедлива оценка

||Аx|| ≤ с ||x|| (2)

для любых x Î X, где с – постоянная.

Теорема 3. Пусть А: X → Y, А – линейный оператор, X, Y – банаховы пространства. Для того чтобы А был непрерывным, необходимо и достаточно, чтобы он был ограниченным.

§2. Норма линейного оператора

В линейном пространстве непрерывных линейных операторов зададим норму следующим образом:

. (1)

Поясним, почему существует конечное число ||А||, определяемое для любого ограниченного оператора равенством (1). Так как А – ограничен, то множество

ограничено сверху. По теореме о верхней грани существует .

Из свойства sup M следует, что ||Аx|| ≤ ||А|| для всех x Î S1(0). Отсюда

||Аx|| ≤ ||А|| ||x||, (2)

справедливое для всех x Î X, включая x = 0. таким образом, ||А|| является наименьшей из констант в неравенстве ||Аx|| ≤ ||А||, и, значит, оценка (2) является наилучшей.

Пространство нормированных непрерывных линейных операторов, действующих из X в Y, будем обозначать L(X, Y).

§3.Обратные операторы

Системы линейных алгебраических уравнений, интегральные уравнения, а также различные задачи для обыкновенных дифференциальных уравнений и уравнений с производными часто могут быть записаны в виде линейного уравнения

Если существует обратный оператор , то решение задачи записывается в явном виде:

Важное значение приобретает теперь выявление условий, при выполнении которых обратный оператор существует и обладает теми или иными свойствами.

Пусть задан линейный оператор: А: X → Y, где X,Y – линейные пространства, причем его область определения D(A)X, а область значений R(A)Y.

Введем множество - множество нулей оператора А. заметим, что N(A) не пусто, так как 0 Î N(A)

Теорема 4. Оператор А переводит D (А) в R (А) взаимно однозначно тогда и только тогда, когда N(A)=, (т.е. множество А нулей состоит только из элемента 0)

Теорема 5. Оператор А-1 существует и ограничен на R(A) тогда и только тогда, когда для некоторой постоянной m>0 и любого x Î D(A) выполняется неравенство

. (1)

Введем теперь следующее важное понятие.

Будем говорить, что линейный оператор А: X → Y непрерывно обратим, если R(A)=Y , оператор обратим и A-1 Î L(Y, X), (т.е. ограничен).

Обращаясь к теореме 5, мы сможем сформулировать следующее утверждение.

Теорема 6. Оператор А непрерывно обратим тогда и только тогда, когда R(A)=Y и для некоторой постоянной m>0 и для всех выполняется неравенство (1).

В случае определенного и ограниченного на всем множестве оператора A Î L(X,Y) имеется теорема Банаха об обратном операторе.

Теорема 7. Если А – ограниченный линейный оператор, отображающий взаимно однозначно банахово пространство X на банахово пространство Y, то обратный оператор А-1 ограничен.

Иными словами, если А Î L(X,Y), где X и Y банаховы, R(A)=Y и А обратим, то А непрерывно обратим.

Взглянем на понятие непрерывно обратимого оператора с точки зрения разрешимости линейного уравнения

Ax = y (2)

Если А непрерывно обратим, то уравнение это имеет единственное решение x = A-1y для любой правой части у. Если при этом (решение того же уравнения с правой частью ), то . Это означает, что малое изменение правой части y влечет малое изменение решения, или, как принято говорить, задача (2) корректно разрешима.

Пусть А Î L(X,Y). Оператор U Î L(X,Y) будем называть правым обратным к А, если AU = Iy. Оператор V Î L(X,Y) будем называть левым обратным к А, если VA = Ix.

Здесь через Iy (Ix) обозначен тождественный оператор в пространстве Y (X). Ниже для правого обратного к А используем обозначение Аr–1, а для левого – АL–1.

Лемма 1. Если существует правый обратный Аr–1 к А, то уравнение (2) имеет решение

x = Аr–1 y

Если существует левый обратный оператор к А, то уравнение (2) может иметь не более одного решения.

Доказательство.

А(Аr–1 y) = (А Аr–1)y = y,

т.е. x = Аr–1 y обращает (2) в тождество и, значит, является решением.

Далее, пусть существует АL–1. рассмотрим N(A). Пусть x Î N(A), тогда Аx = 0. применим к этому равенству оператор АL–1, тогда АL–1Аx = 0, откуда x = 0. итак, всякое x Î N(A) оказывается равным 0. Значит, N(A) = {0} и, по теореме 4, А взаимно однозначен, т.е. для уравнения (2) справедлива теорема единственности. Что и требовалось доказать.

Пусть X – банахово пространство. Рассмотрим банахово пространство L(X) – пространство линейных, ограниченных и заданных на всем множестве операторов. Пусть I – тождественный оператор в L(X). Очевидно, что I непрерывно обратим. Ниже доказывается, что вместе с I непрерывно обратимы все операторы - единичного шара в L(X), т.е. все такие А, для которых справедливо неравенство .

Для краткости положим C = I – A. Ниже мы будем ссылаться на признак Вейерштрасса: пусть X – банахово пространство, тогда всякий абсолютно сходящийся в X ряд сходится.

Теорема 8. Пусть и ; тогда оператор I – C непрерывно обратим. При этом справедливы оценки

(1)

(2)

Доказательство. Рассмотрим в L(X) ряд

I+C+C2+C3+… (3)

Так как , то ряд (3) оценивается сходящимся числовым рядом – геометрической прогрессией

По признаку Вейерштрасса ряд (3) сходится равномерно, т.е.

.

Где S – сумма ряда (3). Далее простой проверкой убеждаемся, что

,

.

Но при этом (ибо и ), а . Поэтому, в пределе имеем равенства (I – C)S = I и S(I – C) = I. По лемме 1 отсюда заключаем, что I – C непрерывно обратим и S=(I – C)-1. Далее,

,

.

Переходя в этих неравенствах к пределу при , получаем оценки (1) и (2). Теорема доказана.

Теперь рассмотрим более общий случай пространства L(X,Y). Пусть А Î L(X,Y) непрерывно обратим.

Теорема 9. Пусть A, B Î L(X,Y), А непрерывно обратим и выполнено неравенство . Тогда B непрерывно обратим и справедливы оценки

, .

§4. Абстрактные функции

Пусть S – некоторое множество на числовой оси или в комплексной плоскости, а X – нормированное пространство.

Рассмотрим функцию x() с областью определения S и с областью значений в X. Такие функции принято называть абстрактными функциями числовой переменной или векторными функциями числовой переменной, поскольку элементы линейного (иначе – векторного) пространства мы называем также векторами. На абстрактные функции числовой переменной переносятся многие понятия и факты математического анализа. Далее рассмотрим сведения о пределах и непрерывности таких функций, о разложении в степенные ряды, а также понятие аналитической абстрактной функции.

Пусть x() определена в окрестности точки 0, за исключением, быть может, самой точки 0. Элемент а Î X будем называть пределом функции x() при →0 и записывать

при →0,

если при →0.

Степенные ряды – это специальный случай рядов в нормированном пространстве, когда члены ряда зависят от параметра.

Рассмотрим в нормированном пространстве X ряд вида , где xк Î X, а – вещественное или комплексное переменное. Поскольку можно ввести новую переменную –0 = , то в дальнейшем мы полагаем 0 = 0 и рассматриваем степенные ряды вида

(1)

Конечная сумма называется частичной суммой степенного ряда (1).

Пусть – множество всех точек , для которых ряд (1) сходится. называется областью сходимости ряда (1).

Сумму ряда (1) при Î обозначим через S() (это абстрактная функция, определенная на со значениями в X), при этом будем писать

, при Î .

Последнее равенство означает, что Sn() → S() при n→∞ для всех Î .

Очевидно, область сходимости любого степенного ряда (1) не пуста, так как 0 Î . Как и в случае скалярных функций, справедлива следующая теорема.

Теорема 10 (Абель). Пусть0 ≠ 0 и 0 Î , тогда круг содержится в . Во всяком круге Sr(0), где r < , ряд (1) сходиться абсолютно и равномерно относительно .

Теорема 11. Пусть два степенных ряда равны в круге SR(0), R>0:

;

тогда равны все их коэффициенты: (k=0, 1, 2, …)

Дифференцирование абстрактных функций

Пусть функция числового переменного λ со значениями в банаховом пространстве X определена в окрестности точки λ0.

По определению производной x’(λ0) функции x(λ) в точке λ0 называется предел

,

если этот предел существует (и конечен). Если имеет производную в точке λ0, то она называется дифференцируемой в этой точке.

§5. Аналитические абстрактные функции и ряды Тейлора

Абстрактную функцию x() будем называть аналитической при =0, если она представима в некоторой окрестности точки =0 сходящимся степенным рядом:

(1)

с ненулевым радиусом сходимости.

Теорема 12. Если x() – аналитическая абстрактная функция при =0, то x() непрерывна в круге SR(0), где R – радиус сходимости степенного разложения (1).

Теорема 13. Если x() – аналитическая абстрактная функция при =0, то x() дифференцируема в круге SR(0) сходимости своего степенного разложения.

Пусть x() бесконечно дифференцируема в точке 0. Ряд вида

называется рядом Тейлора функции x().

Если x() аналитична при =0, то ее ряд Тейлора, в силу теоремы 10, является ее степенным разложением и, значит, сходится к ней в SR(0).

Понятие абстрактной аналитической функции используется в широко применяемом на практике методе малого параметра.

§6. Метод малого параметра в простейшем случае

Рассмотрим следующее уравнение:

Аx –Сx=y. (1)

Здесь А, С Î L(X,Y) и y Î Y заданы, - скалярный параметр, , а неизвестное x разыскивается в X. Если , т.е.

, (2)

то, согласно теореме 9, оператор А–С непрерывно обратим, и тогда решение уравнения (1) существует, единственно и задается явной формулой

. (3)

Отсюда видно, что в круге (2) решение является аналитической функцией параметра и, следовательно, может быть найдено в виде

(4)

На этой идее основывается метод малого параметра для уравнения (1). Подставим ряд (4) в уравнение (1) и, согласно теореме единственности разложения в степенной ряд, приравниваем коэффициенты при одинаковых степенях в правой и левой частях получившегося тождества:

.

Таким образом, мы приходим к следующей рекуррентной системе уравнений для определения x0, x1, …:

Аx0=y, Аx1=Сx0, …, Аxк=Сxк-1, …

Так как А непрерывно обратим, то отсюда последовательно находим

x0=А–1y, x1= А–1(СА–1)y, …, xк= А–1(СА–1)кy, …

Следовательно,

. (5)

Мы получили решение (3), разложенное в степенной ряд. Если мы хотим оборвать степенной ряд и ограничиться приближенным решением

то можно оценить ошибку. Вычитая из ряда (5) его частичную сумму (6) и оценивая разность по норме, получим

.

§7. Метод малого параметра в общем случае

Пусть дано уравнение

А()х = у(). (1)

Здесь А()Î L(X,Y) задана при каждом , , или, как говорят, А() – оператор-функция. Пусть А() аналитична при =0, а оператор А(0) непрерывно обратим, у() – заданная аналитическая функция при =0 со значениями в Y. Неизвестное x разыскивается в X.

Аналитичность А() и у() в точке 0 означает, что они разлагаются в следующие степенные ряды с ненулевыми радиусами сходимости, которые равны и соответственно:

, . (2)

Из аналитичности А() следует непрерывность А() при =0. следовательно, найдется число r > 0 такое, что в круге

.

Отсюда вытекает, что в круге оператор-функция А() непрерывно обратима и, следовательно, уравнение (1) имеет единственное решение

,

при этом x() аналитична в точке =0 и радиус сходимости соответствующего степенного ряда равен min(, r). Для фактического построения x() удобно воспользоваться методом малого параметра. Будем разыскивать x() в виде

. (3)

Подставляя ряд (3) в уравнение (1) и учитывая разложения (2), приходим к следующей системе для неопределенных коэффициентов x0, x1, x2, …:

А0x0 = y0, А0x1+А1x0 = y1,

А0x2 + А1x1 + А2x0 = y2, (4)

. . . . . . . . . . .

, …

Здесь А0 = А(0) непрерывно обратим. Решая последовательно уравнения получившейся системы, находим

, , … (5)

Возникающие здесь формулы довольно громоздки, однако этим путем можно найти решение уравнения с любой степенью точности. Метод малого параметра особенно удобен в тех случаях, когда обращение оператора А(0) – задача более простая, чем задача обращения оператора А().

§8. Метод продолжения по параметру

8.1. Формулировка основной теоремы

В качестве еще одного приложения теорем об обратных операторах рассмотрим один из вариантов метода продолжения по параметру. Пусть и А непрерывно обратим. Если , то, согласно теореме 9 §3, В также непрерывно обратим. Оказывается, при определенных условиях можно доказать, что В будет непрерывно обратим и в том случае, когда он очень далек от А. Идея заключается в следующем. Рассмотрим непрерывную на отрезке [0, 1] оператор - функцию такую, что А(0)=А, А(1)=В. Иначе говоря, в L(X, Y) рассматривается непрерывная кривая, соединяющая точки А и В. Будем предполагать, что для оператор – функции выполняется следующее условие:

Существует постоянная такая, что при всех и при любых справедливо неравенство

. (1)

Ниже будет доказана следующая теорема.

Теорема 14. Пусть А(λ) – непрерывная на [0, 1] оператор-функция (при каждом ), причем оператор А(0) непрерывно обратим. Если для А(λ)выполняется условие I, то А(I)непрерывно обратим, причем .

Замечание к теореме 14. Если выполнено условие I при и оператор непрерывно обратим, то

. (2)

Действительно, пусть , а , т.е.. тогда условие I дает или , что означает справедливость неравенства (2).

8.2. Простейший случай продолжения по параметру

Приведем здесь доказательство теоремы 14 для случая, когда . Согласно условию этой теоремы . По замечанию 14 . Имеем следующую оценку:

.

Пусть , где . На [0, δ] имеем , и, следовательно, по теореме 9 А(λ) при всяком непрерывно обратим. Если окажется, то , то теорема доказана.

Пусть δ < 1. Возьмем А(δ). Согласно замечанию п.14.1 . Повторяем наши рассуждения при λ>δ. Имеем оценку

,

если , откуда А(λ) непрерывно обратим при каждом . Если , то теорема доказана. Если же 2δ < 1, то 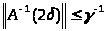и рассуждение можно повторить. После конечного числа шагов мы достигаем точки λ=1, и, следовательно, А(1) непрерывно обратим.

Доказательство теоремы в общем случае

Рассмотренный выше частный случай отрезка в L(X,Y) не всегда удобен в приложениях. Общий случай основывается на следующем элементарном предложении.

Лемма. Пусть М – некоторое непустое множество на [0,1], одновременно открытое и замкнутое на [0.1]. тогда М=[0, 1].

Замечание 1. условие открытости М на [0,1] понимается так: для любого существует δ > 0 такое, что .

Доказательство леммы. Пусть N = [0, 1] \ M (дополнение к М на [0, 1]). Нужно доказать, что N = Æ – пустое множество. Допустим противное, что N ¹ Æ. Поскольку М ¹ Æ и ограничено сверху, то существует b = supM, причем b Î M вследствие замкнутости. Покажем, что b = 1. Если b <1, то вследствие открытости M на [0, 1] найдется x > b, x Î M. Это противоречит определению supM. Следовательно, b >1 невозможно. Итак, 1Î М.

Теперь рассмотрим множество N. Как дополнение к М, оно также открыто и замкнуто на [0, 1], и, значит, к нему применимо рассуждение с supM . мы получаем, что 1 Î N. Это невозможно, ибо N – дополнение к М. полученное противоречие доказывает, что допущение N ¹ Æ неверно. Итак, N= Æ, т.е. М = [0, 1]. Лемма доказана.

Вернемся к доказательству теоремы. Пусть М – множество тех точек λÎ[0, 1], для которых оператор А(λ) непрерывно обратим. Согласно замечанию 1 для всех λ Î М. М не пусто, поскольку 0 Î [0, 1].

воспользуемся непрерывностью оператор–функции А(λ) в метрике L(X,Y). Для любого e > 0 найдется δ = δ(e)>0 такое, что при всех λ Î [0, 1] таких, что < δ выполняется неравенство <e.

Возьмем e = γ, тогда при < δ(γ), λ Î [0, 1]

<1.

По теореме 9 §3 А(λ) непрерывно обратим для всех таких λ. Итак, вместе с λ0 М содержит , т.е. М открыто на [0, 1].

Докажем, что М замкнуто на [0, 1]. Пусть и при . Надо доказать, что λ0 М. воспользуемся неравенством и получим

.

Вследствие непрерывности А(λ) по λ для любого e > 0 находим номер N = N(e) такой, что при n > N будет <e. Возьмем e = γ, тогда для n = N(γ)+1 <1.

По теореме 9 А(λ0) непрерывно обратим, т.е. λ0 Î М, и, значит, М замкнуто на [0, 1]. По лемме М = [0, 1] . в частности, 1Î М и . Теорема полностью доказана.

Замечание. Рассмотрим уравнение с параметром:

А(λ)х = у, λÎ [0, 1]. (1*)

Пусть для всех возможных решений этого уравнения при всяком λÎ [0, 1] справедлива оценка

, (2*)

где с – некоторая постоянная, не зависящая от х, у и λ. Оценка такого рода называется априорной оценкой для решения уравнения (1*). Очевидно, априорная оценка (2*) представляет собой лишь иначе записанное условие (1): .

Доказанная выше теорема свидетельствует о важности априорных оценок для доказательства теорем существования и единственности решений.

Глава 2. Приложение

Пример 1. Рассмотрим интегральное уравнение с малым вещественным параметром λ:

(1)

Это уравнение вида А()х = у() – операторное уравнение в С[-π; π], где

Покажем, что А() аналитична в т. 0, т.е. разлагается в ряд вида . Разложим функцию А() в ряд Тейлора: .

Найдем к – ую производную:

Разложим функцию в ряд Тейлора в т. 0:

Таким образом, функция аналитична, следовательно, непрерывна при = 0, а значит, уравнение имеет единственное решение.

Операторные коэффициенты имеют вид:

; (2)

I. Начнем с уравнения А0x0 = y системы (4) §7, где у нас теперь y0=y, yк=0, к ≥ 1.

Заменим, , поэтому

, (4)

где

,

Для того, чтобы найти коэффициент А в уравнении (4), умножим его на cos t и, интегрируем по t от –π до π:

,

подсчитаем интегралы:

, ,

Тогда, подставив в уравнение, получаем: . Отсюда:

. (5)

Найдем коэффициент В уравнения (4), умножив это уравнение на sin t и интегрируя по t от –π до π:

.

Подсчитав соответствующие интегралы:

, , , подставив и выразив В, получаем:

. (6)

Подставим найденные коэффициенты (5) и (6) в уравнение (4):

и свернем по формуле:

II. Найдем теперь x1(t), для этого необходимо решить следующее уравнение системы (4) §7: А0x1+А1x0 = y1. Так как y1=0 в нашем случае, то мы будем решать уравнение А0x1= – А1x0.

Обозначим , т.к. мы знаем теперь x0(s), следовательно φ(t) можно вычислить. Имеем:

Как в предыдущем случае заменим, , поэтому

. (7)

где , .

Умножим уравнение (7) на cos t и проинтегрируем по t от –π до π – получим коэффициент А:

Подсчитав: , , ,

имеем .

Аналогично умножив уравнение (7) на sin t и проинтегрируем по t от –π до π – получим коэффициент В: .

Составляем функцию x1(t), подставив коэффициенты А и В в уравнение и свернув равенство по формуле косинуса разности:

.

Таким способом мы можем найти все остальные решения уравнения с любой степенью точности.

Пример 2. Применим метод продолжения по параметру для оценки разрешимости краевой задачи для дифференциального уравнения, а потом решим ее методом малого параметра.

–x'' + b(t)x' +c(t)x = y(t), 0< t <1, (1)

x(0) = x(1) = 0 (2)

Здесь c(t) непрерывна на [0, 1], b(t) непрерывно дифференцируема на [0, 1]. Предположим еще, что на [0, 1] c(t) – b(t)'/2 ≥ α > –8/π (*).

Покажем методом продолжения по параметру, что в этих условиях при всякой правой части y ÎY = С [0, 1] существует единственное решение задачи x Î X = С2 [0, 1] – пространству, состоящему из дважды непрерывно дифференцируемых на [0, 1] функций x(t), удовлетворяющих граничным условиям (2), и с нормой , где .

Запишем задачу (1) – (2) в операторном виде: Вx = y

Здесь определен всюду на X со значениями в Y. В качестве оператора А примем ÎL(X, Y).

Соединим операторы А и В отрезком

, λ Î [0, 1].

Теперь необходимо установить априорную оценку для решений краевой задачи

–x'' + λb(t)x' + λc(t)x = y(t), 0< t <1, (3)

x(0) = x(1) = 0 (4)

Как только такая оценка будет получена, из теоремы п.8.1. будет следовать однозначная разрешимость краевой задачи (3) – (4).

Умножим уравнение (3) на x(t) и проинтегрируем полученное равенство по t от 0 до 1:

.

Заметим, с учетом граничных условий:

Подставим полученные интегралы и сгруппируем относительно λ:

(5)

Произведем оценку всех трех слагаемых в этом равенстве.

Докажем, что . (6)

Заметим, что , и значит по неравенству Коши – Буняковского:

.

Точно так же:

.

Перемножим эти неравенства:

. (6*)

Отсюда, замечая, что , получим

.

Далее (7)

– это следует из предположения (*).

Последний интеграл равенства (5) можно оценить, используя скалярный квадрат:

, где .

Для любого ε > 0

. (8)

Используя полученные неравенства (6), (7), (8) и подставляя их в равенство (5), получаем:

,

считая ε > 0 достаточно малым, имеем

.

Выберем и получим

, где .

Возвращаясь снова к равенству (5), получим следующую оценку:

, где , а .

Теперь с помощью оценки (6*) имеем и, значит, учитывая, что , получим

(9)

Из уравнения (3) можем получить оценки для и :

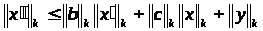. (10)

Здесь оценивается через и . Действительно, x(0) = x(1) = 0. по теореме Роля на (0, 1) найдется точка ξ, в которой x'(ξ) = 0. Тогда, запишем уравнение (3) в виде

,

(в этом можно убедиться, взяв производную:

и сократив)

интегрируем его от ξ до θ и получим

.

Отсюда имеем оценку

, (11)

где .

Теперь подставим полученные результаты в (10):

. (12)

Теперь (9), (11) и (12) дают искомую априорную оценку:

(постоянную с4 нетрудно подсчитать, сложив неравенства(9), (11), (12)и выполнив преобразования).

Таким образом, доказательство разрешимости задачи получено, теперь приступим к ее решению методом малого параметра.

Итак, рассмотрим операторное уравнение:

А(λ)x = y(λ),

где .

I. Начнем с уравнения А0x0 = y (где А0 – коэффициент при нулевой степени λ) системы (4) §7, причем y0 = y, yк = 0, к ≥ 1.

, причем с1 подбирается так, чтобы выполнялось краевое условие: x0(1) = 0.

II. Найдем x1(t), для этого необходимо решить следующее уравнение: А0x1+А1x0 = y1. Так как y1=0, то мы будем решать уравнение А0x1= – А1x0.

Из того, что следует следующее уравнение:

.

По аналогии c2 и c3 подбираем так, чтобы выполнялось краевое условие: x0(1) = 0.

Таким образом, решения нашей краевой задачи выглядит так:

,

подставляя найденные решения, имеем:

или

Список литературы

Данфорд Н., Шварц Дж. Линейные операторы. М., 1962

Талдыкин А.Т. Элементы прикладного функционального анализа: Учеб. пособие. – М.: Высшая школа, 1982.

Треногин В.А. Функциональный анализ. М., 1993.

Функциональный анализ./Под. ред. С. Г. Крейна. М., 1972

Хатсон В., Пим Дж. С. Приложения функционального анализа и теория операторов. Пер. с англ. – М.: Мир, 1983.

Для подготовки данной работы были использованы материалы с сайта http://revolution.allbest.ru/